考虑温度的高速列车轴箱轴承内部接触特性分析

江志伟,王志伟,楚 明,莫继良,赵 婧

(西南交通大学 机械工程学院摩擦研究所, 成都 610031)

0 引言

随着国内高速列车运行速度进一步的提高,列车的运行安全面临着更大的挑战。轴箱轴承作为高速列车运行件的核心部件之一,在高速和重载的服役环境下,各零部件之间摩擦热问题较为显著。温度升高引起的热膨胀变形会对轴承承载特性、内部接触力学特性等产生显著影响[1-5]。特别地,由于某种异常原因使得轴承热量迅速增加时,其工作温度将继续升高,进而造成轴承失效,严重威胁车辆安全运行。因此,亟需开展考虑温度的高速列车轴承热力耦合分析,保证列车安全运营。

许多学者基于理论分析、数值仿真和实验手段围绕轴承温度开展了大量研究。Palmgren[6]基于大量的实验研究分析,提出了摩擦功耗计算公式,该公式计算方法简单可靠,可用于计算轴承整体的摩擦功耗。Hrris[7]以轴承动力学理论为基础,根据轴承各零部件间的受力关系,总结了一种局部计算轴承摩擦功耗的方法。Pouly等[8]利用热网络法研究了高速轴承功率损耗,发现与其他功率损耗相比,滚动摩擦和阻力损失是两个最主要的损耗来源。徐建宁等[9]基于传热学和摩擦学原理建立了滚动轴承有限元模型,分析了热平衡状态下轴承的温度和热变形。Wang等[10]利用有限元方法建立了圆柱滚子轴承温度场仿真模型,分析了不同润滑剂对轴承温度的影响规律。汤武初等[11]利用有限元方法分析了健康与故障下轴承的温度分布,并通过实验分析了影响轴承温度的关键因素。Zhou等[12]基于光纤布拉格光栅的方法建立了轴承温度实验台,分析了转速和径向载荷对轴承内外圈温升的影响规律。Wang等[13]利用SIMPACK建立了包含轴承的车辆动力学模型,研究了轨道不平顺引起的车辆振动下轴承的热特性以及关键因素对轴承工作温度的影响。高朋等[14]建立了中介轴承瞬态热传递模型,研究了环境温度、润滑剂运动黏度和转速对轴承摩擦热和温度的影响。Mitrovic等[15]建立了球轴承二维模型,分析温度对热膨胀、刚度的影响。郝旭等[16]基于ANSYS建立了二维轴承热力耦合模型,研究了转速、润滑油温度与流速对轴承内外圈位移和滚道应力的影响特性。

综上所述,目前国内外对轴承的研究主要集中在轴承的摩擦功耗和温度分析方面,关于轴承温度如何影响接触特性的研究较少,对高速列车轴箱轴承的热力耦合分析的研究鲜见报道。实际服役过程中,高速列车轴箱轴承内部摩擦、温度与振动三者间相互影响。然而,轴承内部接触状态极其复杂,且难以准确掌握,直接影响列车运行安全。为此采用有限元方法建立了高速列车轴箱轴承热力耦合模型,系统研究了轴箱轴承内部的温度分布规律以及温度对轴承接触特性的影响规律,并进一步探究了复合载荷和转速对轴承温度和接触特性的影响规律。

1 模型的建立

我国高速列车轴箱轴承通常采用双列圆锥滚子轴承。综合考虑计算效率、精度、结构及载荷的对称性,模型可简化为单列圆锥滚子。简化前后的高速列车轴箱轴承三维模型如图1所示。

1.1 高速列车轴箱轴承发热模型和对流换热模型

1) 轴承发热模型。

目前,国内外有关轴承热量计算的模型主要有Palmgren发热量模型、Harris发热量模型、SKF发热量模型和近似发热量模型[17]。其中,Palmgren发热量模型和近似发热量模型可适用于高速列车轴箱轴承。但相比近似发热量模型,Palmgren发热量模型更接近实验效果,准确性更高[17],因此研究中选择Palmgren发热量模型计算高速列车轴箱轴承发热功率。

Palmgren发热量模型包含2部分,分别为由外载荷和润滑剂粘性摩擦引起的摩擦力矩。Palmgren经验公式可表示为[18]:

M=Mi+Mv

(1)

式中,Mi和Mv分别为外载荷和润滑剂粘性摩擦引起的摩擦力矩。

外载荷引起的摩擦力矩Mi为:

Mi=f1Fβdm

(2)

式中,f1为载荷系数,且f1=z(Fs/Cs)y,z和y是与轴承结构类型相关的系数,Fs为当量静载荷,Cs为基本额定静载荷;dm为轴承节圆直径;对于圆锥滚子轴承,Fβ=0.4Fr+0.4cosαFa,Fa为径向载荷,Fr为轴向载荷,α为接触角。

润滑剂粘性摩擦引起的摩擦力矩Mv为:

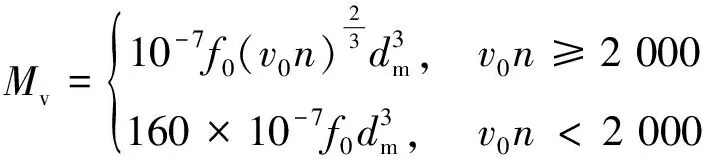
(3)

式中,v0为润滑剂的运动粘度;n为轴承转速;f0为与轴承类型、润滑方式有关的系数。

根据式(2)和式(3)计算的摩擦力矩得到的总发热量为:

Ht=πn(Mi+Mv)/30

(4)

对于整个轴承,热源连续通过接触区域,因此,可根据接触区域表面产生的热量,然后平均计算其热通量密度,计算公式为:

q=H/S

(5)

式中,H为发热量;S为接触面积。

对于圆锥滚子,S计算式为:

(6)

2) 轴承对流换热模型。

目前,轴承对流换热模型主要为Harris对流换热模型。Harris对流换热模型给出的传统轴承内腔与润滑剂间的换热系数为[19]:

(7)

式中,k为导热系数;Pr为普朗克常数;u为润滑油相对热交换表面的流速;v为润滑油的粘度;x为特征长度。对于内滚道,u取内圈速度,x取内滚道直径;对于外滚道,u取保持架速度,x取轴承节圆直径。

轴承座外表面与空气对流换热系数为[19]:

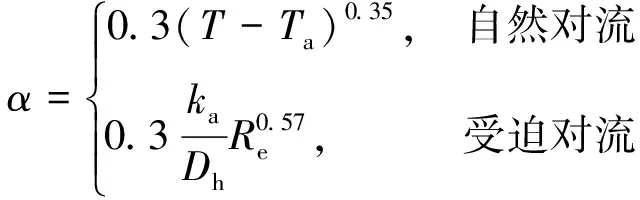
(8)

式中,Ta为轴承座外表面环境温度;Dh为轴承座外表面直径;ka为空气导热系数。

Re计算式为:

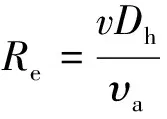
(9)

式中,v为气流速度;υa为空气运动粘度。

1.2 高速列车轴箱轴承稳态温度场模型

为研究高速列车轴箱轴承实际工作中内部的温度分布情况,建立了轴箱轴承稳态温度场有限元模型。主要几何参数和材料参数分别如表1和表2所示。

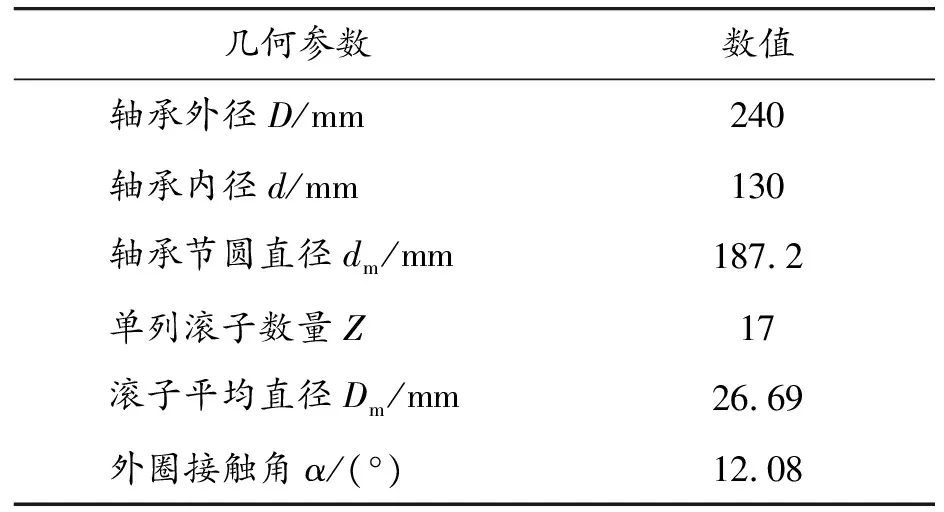
表1 高速列车轴箱轴承主要几何参数

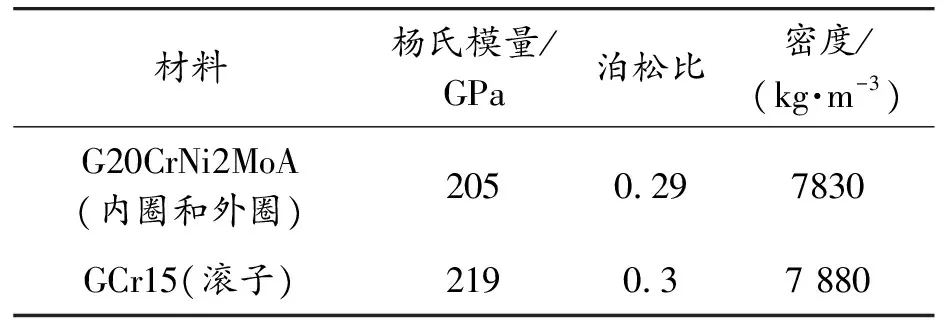
表2 高速列车轴箱轴承各零件材料参数

1) 网格划分。

有限元模型网格的数量和质量直接影响仿真结果的精度,网格数量过多会增加CPU的计算时间,并对计算机的内存提出更高的要求。综合考虑圆锥滚子轴承有限元模型的特点与计算机的配置,对内外圈采用Hex dominant method进行划分,全局网格尺寸定义为1.2 mm;滚子采用MultiZone划分网格,全局网格尺寸定义为1.0 mm。各零部件网格划分完成后如图2所示,最终轴承有限元模型共896 752个网格单元和942 815个网格节点。

图2 高速列车轴箱轴承温度场有限元网格模型示意图

2) 接触设置。

在轴承温度场分析过程中需要定义合适的接触方式,否则难以准确反映内部温度特性。根据轴承实际工作情况,需要设置2组接触对,分别为滚子表面与外圈滚道、内圈滚道接触对。在滚子-外圈接触对中,选取外圈滚道为目标面,滚子圆锥面为接触面;在滚子-内圈接触对中,选取内圈滚道为目标面,滚子圆锥面为接触面。接触类型均为不分离接触,接触算法选用增强的拉格朗日算法。

3) 边界条件和热载荷设置。

在ANSYS软件温度场分析模块中,热载荷类型主要为heat flow(热流量)、perfectly insulated(完全绝热)、heat flux(热通量)和internal heat generation(内部生成热)。由于轴承各零部件的材料物理性能是类似的,因此摩擦热在接触区域上可按1∶1分布[20-21],内外圈各占总热量的1/4,滚子占总热量的1/2。轴承工作时,内圈和滚子会周期性旋转,故假设内外圈和滚子的总热量是均匀分布在接触面上的。根据式(1)—式(4)计算出轴承总发热量,再根据式(6)计算出接触区域面积,最终可得到施加在滚子和内外圈接触面的热通量密度[20,22]。此外,轴承内外圈、滚子与润滑剂或空气的热对流系数由Harris换热公式确定,系数计算结果如表3所示。

表3 系数计算结果

1.3 高速列车轴箱轴承静力学有限元模型

为进一步研究轴承内部温度对接触特性的影响,建立了高速列车轴箱轴承三维静力学模型。其中,零部件材料、网格划分与稳态温度场模型保持一致,仅改变接触设置、边界条件和载荷设置。

在静力学有限元模型中,内外圈滚道与滚子的接触类型为摩擦接触,摩擦因数为0.01[23],接触算法设置为增强的拉格朗日算法。此外,轴承外圈外表面完全固定,约束其6个自由度;对内圈的端面进行轴向约束,限制端面的移动;建立全局柱坐标系,模拟保持架约束所有滚子的转动;轴承内圈内表面施加22.5 kN的轴承力,详细设置如图3所示。

图3 轴箱轴承静力学模型边界与载荷设置示意图

2 模型验证

2.1 轴承稳态温度场模型实验

为验证轴承温度场模型的准确性,开展了高速列车线路实验,轴承温度传感器布置如图4所示。列车稳定运行速度为300 km/h,列车从0加速到300 km/h大概耗时20 min,轴箱轴承转速为1 730.8 r/min,双列圆锥滚子轴承径向载荷和轴向载荷分别为45 kN和10 kN左右[24]。通过温度传感器采集轴箱轴承温度,结果如图5所示。由此可知,轴承温度从35.06 ℃逐渐上升,20 min时,轴承转速已经达到稳定,但是温度还在持续上升;60 min附近时温度达到72 ℃,随后温度开始趋于平稳,始终在70～80 ℃之间波动。

图4 高速列车线路实验场景图

图5 轴箱轴承温度变化曲线

为了进行模型对比验证,开展仿真分析。为保持高速列车运行速度一致(300 km/h),轴箱轴承转速为1 730.8 r/min,单列轴承径向载荷为22.5 kN,轴向载荷为10 kN。轴承有限元模型温度场分布情况计算结果如图6所示。可以看出,内外圈滚道与滚子表面接触区域温度较高,这是因为滚子与滚道摩擦生热,且与外部的散热较少。另外,轴承外圈、内圈和滚子最高温度分别为73.896、74.205、2.171 ℃,相差不大,且与高速列车线路实验结果基本一致,验证了模型的准确性。因此,轴承温度场模型是有效可靠的,可用于研究轴箱轴承的温度场分布以及热特性。

图6 高速列车轴箱轴承温度云图

2.2 轴承静力学有限元模型理论验证

另一方面,为验证轴箱轴承三维静力学有限元模型,通过赫兹接触理论计算内外圈和滚子最大接触应力理论值,并与有限元结果进行对比分析。基于赫兹理论,轴承内部最大接触应力为[25]:

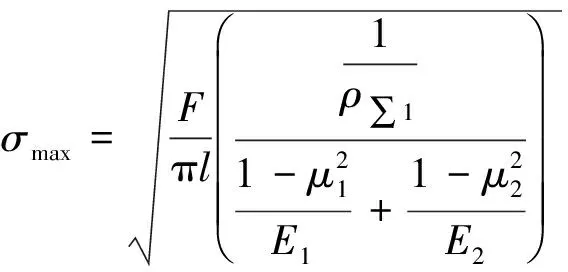
(10)

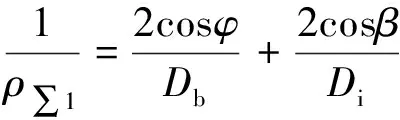
(11)

式中,φ和β分别为滚子半锥角和内圈滚道接触角;Db和Di分别为滚子中部直径和内圈滚道中点处直径。对于圆锥滚子轴承,外载荷F为:

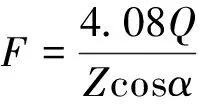
(12)

式中,Z为滚子个数;Q为轴承径向载荷;α为内圈滚道接触角[26]。

根据式(10)—式(12)可计算不同径向载荷下内圈滚道与滚子间接触应力,再对比轴承静力学有限元模型求解的接触应力,结果如表4所示。

表4 静力学模型和赫兹理论法内圈与滚子接触区域应力对比

由表4可知,当轴箱轴承径向载荷在20～25 kN 时,静力学有限元模型与赫兹理论公式求解得到的最大接触应力误差均小于4%,有限元模型结果与赫兹理论结果基本吻合。因此,高速列车轴箱轴承三维静力学有限元模型是有效可靠的,可用于研究轴箱轴承内部不同部件间的接触特性。

3 温度对轴承内部接触特性的影响

为研究温度对接触特性的影响,在轴承静力学模型的基础上,将轴承温度场模型求解的温度作为静力学模型中的载荷边界,构建了考虑温度的高速列车轴箱轴承热力耦合模型,具体流程如图7所示。

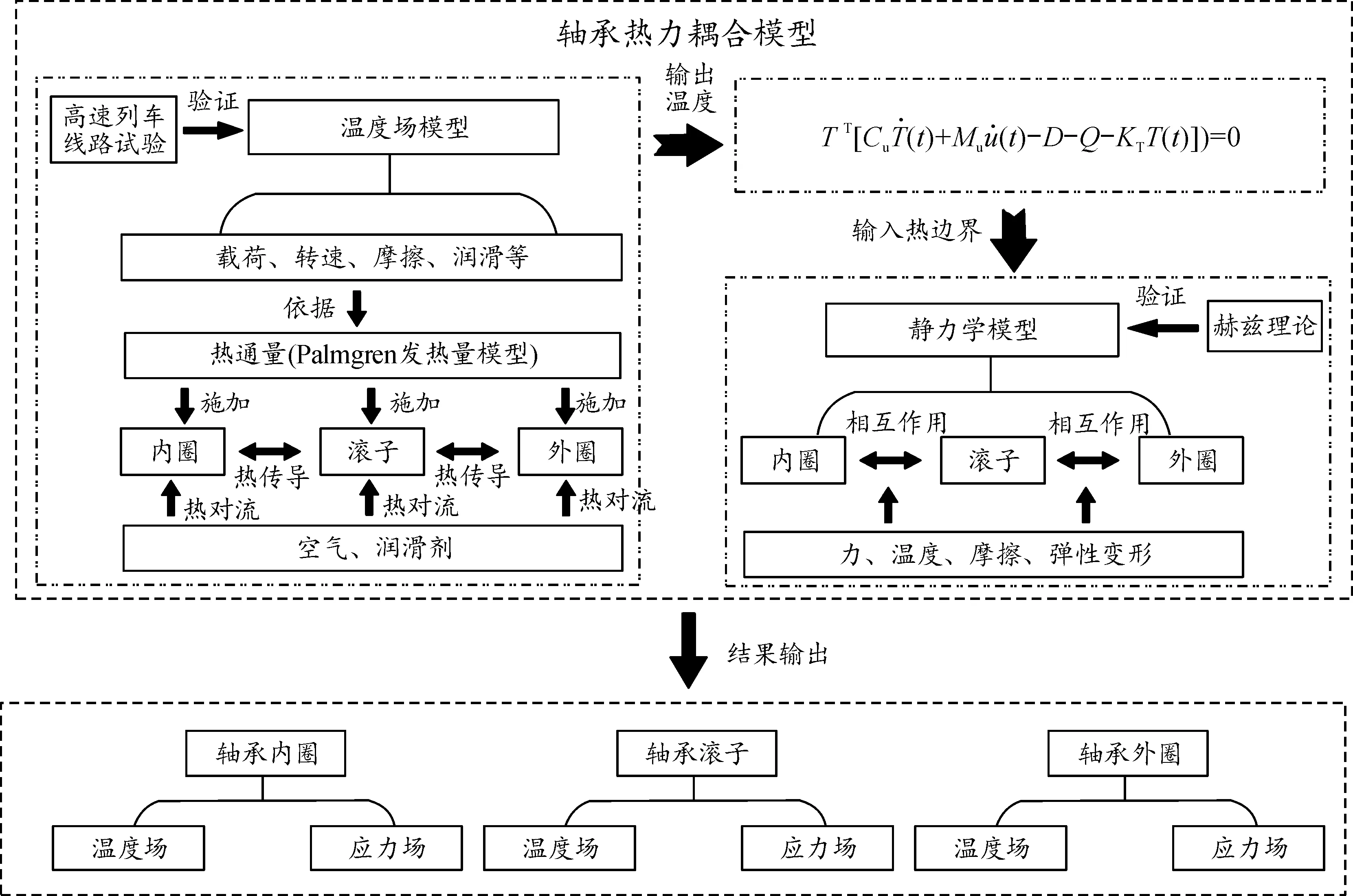
图7 热力耦合分析方法流程框图

图8和图9分别表示不考虑温度和考虑温度情况下,轴承热力耦合模型的等效应力分布结果。其中,轴承内圈轴向载荷和径向载荷分别为10 kN和22.5 kN。

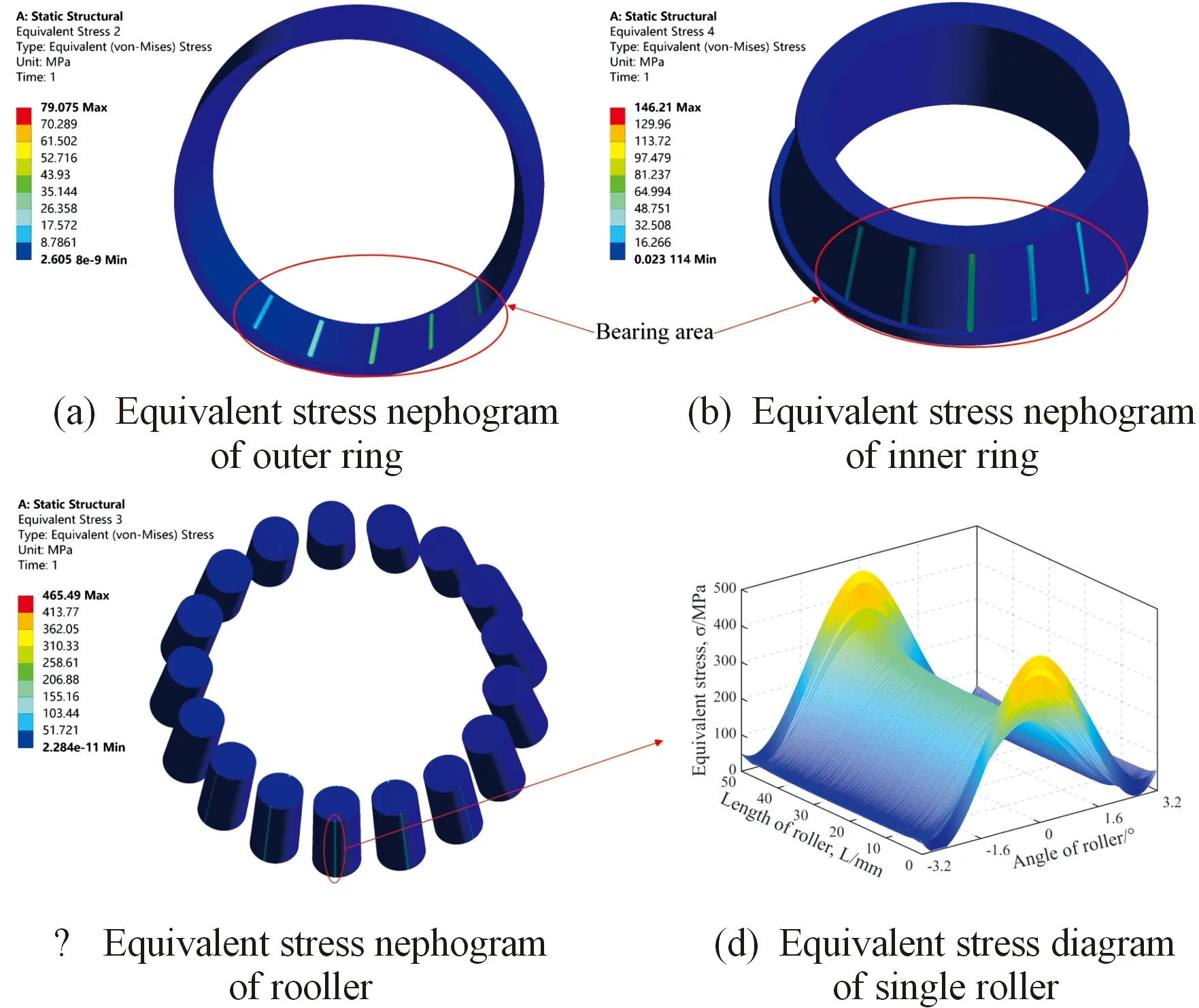
图8 不考虑温度下轴承等效应力分布云图

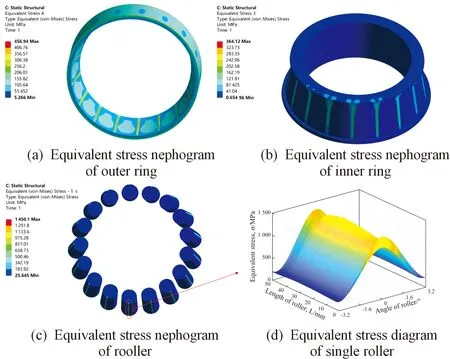
图9 考虑温度下轴承等效应力分布云图

从图8可以看出,轴承内圈、外圈和滚子最大等效应力分别为146.21、79.072、465.49 MPa,并且轴承内外圈滚道只有局部区域以及少数几个滚子出现应力分布,根据是否有应力可将其划分为承载区和非承载区。这是因为虽然轴承内圈同时受到轴向载荷和Y轴正向径向载荷,但是径向轴荷大于轴向载荷,径向载荷起主导作用,轴承内圈最终沿着Y轴正方向移动并挤压滚子,滚子进而挤压外圈。因此,在Y轴正方向上,内外圈滚道与滚子接触产生应力,该区域为承载区;在Y轴负方向上,滚子与内外圈实际是没有接触的,故而该区域为非承载区。

从图9可以看出,在考虑轴承滚子由于自转与内外圈发生摩擦生热的情况下,轴承内圈、外圈和滚子最大等效应力分别为364.12、465.94、1 450.1 MPa,相较于不考虑轴承内部摩擦生热和温升,轴承内圈、外圈和滚子最大等效应力分别增加149.04%、489.26%和211.73%。这是因为轴承内部发生摩擦生热后温度上升,内外圈与滚子在温升的作用下发生热膨胀,体积增大互相挤压进而导致接触区域应力显著增大。此外,在不考虑轴承温升情况下,内外圈与滚子接触区域分为承载区和非承载区。在非承载区,滚子与内外圈存在间隙,但是在考虑轴承温升后,由于内外圈与滚子发生膨胀,体积增大导致间隙被消除,内外圈与滚子接触并挤压产生应力,使得所有滚子均存在不同程度的承载。

图8(d)和图9(d)分别为不考虑温度和考虑温度下的滚子与滚道接触区域应力分布图。可以看出,应力主要分布在滚子角度-3.2°～3.2°之间,呈现对称分布。由于“边界效应”的影响,等效应力在滚子母线方向上呈现“两端大、中间小”的特点[27]。不考虑温度情况下,滚子两端等效应力约为465 MPa,比中间等效应力(约为255 MPa)大了约82.35%;考虑温度情况下,滚子两端等效应力约为1 450 MPa,比中间等效应力(约为1 375 MPa)大了约5.45%。对比发现,不论是否考虑温度,滚子应力都会出现“边界效应”,但是在考虑温度影响下,“边界效应”的影响程度更小了。这是因为考虑温度后热膨胀效应使得滚子与滚道间的接触状态发生改变,内部相互挤压,接触区域应力显著增大,使得由几何因素产生的“边界效应”对应力的影响显著减小。

4 载荷和转速对轴承温度和接触特性的影响

为进一步研究轴承径向载荷、轴向载荷以及转速对轴承温度和内部接触特性的影响,基于热力耦合模型,选取了径向载荷和轴向载荷复合组成的25种工况以及6种不同速度工况进行仿真分析。其中,25种不同载荷工况由5种径向载荷(20、21.25、22.5、23.75、25 kN)和5种轴向载荷(5、7.5、10、12.5、15 kN)复合组成,不同载荷工况下高速列车速度均为300 km/h;高速列车6种不同速度分别为100、150、200、250、300、350 km/h,不同速度工况下轴承径向载荷和轴向载荷分别为22.5 kN和10 kN。

4.1 载荷对轴承温度和接触特性的影响

环境温度22 ℃,高速列车速度300 km/h,热平衡状态下复合载荷对轴承内外圈和滚子的温度、等效应力的影响分别如图10和图11所示。可以看出,当轴向载荷为15 kN时,随着径向载荷从20 kN逐渐增大到25 kN,轴承内圈、外圈和滚子最高温度分别从78.22、77.81、76.03 ℃增加到86.24、85.86、83.73 ℃,增幅分别为10.25%、10.35%和10.13%;轴承内圈、外圈和滚子最大等效应力分别从373.98、494.99、1 560.9 MPa增加到516.84、572.96、1 826.70 MPa,增幅分别为38.20%、15.76%和17.03%。

图10 不同复合载荷下轴承内外圈和滚子最高温度

图11 不同复合载荷下轴承内外圈和滚子最大等效应力

当轴承径向载荷为25 kN时,随着轴向载荷从5 kN逐渐增大到15 kN,轴承内圈、外圈和滚子最高温度分别从70.19、69.84、68.31 ℃增加到86.24、85.86、83.73 ℃,增幅分别为22.86%、22.94%和22.57%;轴承内圈、外圈和滚子最大等效应力分别从353.91、422.32、1 341.00 MPa增加到516.84、572.96、1 826.70 MPa,增幅分别为46.04%、35.67%和36.22%。

通过分析不同载荷下轴承温度和应力的变化,发现当轴承轴向载荷或径向载荷增大时,相较于温度的增幅,最大等效应力的增幅更加显著。这是因为应力一部分是由载荷作用在内圈上直接产生的,另一部分是温升导致热膨胀变形使得轴承内部挤压产生的。

4.2 转速对轴承温度和接触特性的影响

环境温度22 ℃,轴箱轴承径向载荷和轴向载荷分别为22.5 kN和10 kN,热平衡状态下转速对轴承内外圈和滚子温度、等效应力的影响分别如图12和图13所示。

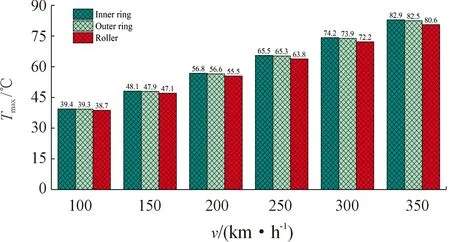
图12 不同转速下轴承内外圈和滚子最高温度

图13 不同转速下轴承内外圈和滚子最大等效应力

可以看出,随着高速列车速度从100 km/h逐渐增加到350 km/h,轴承内圈、外圈和滚子最高温度分别从39.41、39.28、38.73 ℃增大到82.94、82.49、80.56 ℃,增幅分别为110.44%、109.99%和107.99%;轴承内圈、外圈和滚子最大等效应力分别从172.91、211.8、744.84 MPa增大到485.52、537.19、1 725.50 MPa,增幅分别为180.71%、153.63%和131.66%。

5 结论

采用有限元方法建立了高速列车轴箱轴承热力耦合模型,模型考虑了润滑剂对轴承内部摩擦产热和散热的影响。通过线路实验与理论结果进行了验证。系统研究了轴箱轴承内部的温度分布规律以及温度对轴承接触特性的影响规律,进一步探究了复合载荷和转速对轴承温度和接触特性的影响规律。主要结论如下:

1) 温度对轴承特性影响显著,考虑温度情况下轴承内圈、外圈和滚子等效应力分别为364.12、465.94、1 450.10 MPa,与不考虑温度相比分别增加了149.04%、489.26%和211.73%。

2) 载荷对轴承温度和应力有显著影响,载荷增大会导致轴承温度上升和应力增大,且应力增幅更大。当轴向载荷为10 kN,径向载荷为25 kN时,相比于径向载荷为20 kN时,轴承内圈、外圈和滚子最高温度分别增加了11.44%、11.42%和11.29%,最大等效应力分别增加了49.33%、19.55%和20.26%。

3) 转速对轴承温度和应力有显著影响,转速增加会导致轴承温度上升和应力增大。与100 km/h相比,列车以350 km/h运行时的轴承内圈、外圈和滚子最高温度分别增加了110.44%、109.99%和107.99%,最大等效应力分别增加了180.71%、153.63%和131.66%。

由于计算机仿真算力的局限性,建立的是稳态条件下的轴承热力耦合模型,在后期研究中可进一步考虑真实工况下轴承的高速转动及温度的动态变化,实现振动与温度的耦合,以更加真实地反映轴承实际服役情况。