面向批量订单包装的物流箱规格优化问题研究
柳雅真,王利强,2
面向批量订单包装的物流箱规格优化问题研究
柳雅真1,王利强1,2*
(1.江南大学 机械工程学院,江苏 无锡 214122;2.江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
针对面向仓储物流环境下多型号多批量产品的订单包装问题,提出一种预制物流箱规格优化模型及算法。对产品订单建立订单分包规则,确定分包方案,以订单包装材料总成本最小为优化目标建立物流箱规格优化模型。针对该模型提出一种改进模拟退火算法,通过贪婪策略求解最优分包方案,降低模型计算复杂度,设计一种新型解更新算子,以提高算法寻优能力,设计一种自适应步长策略,以平衡算法前期全局搜索与后期局部搜索的能力。通过实例证明,文中提出的算法相较于其他算法,具有更强的求解能力,与实例企业仓储包装现状相比,同批订单降低了17%的包装材料成本。该方法可用于解决产品种类多、尺寸差异大、动态更新等应用场景下的系列运输包装纸箱规格优化问题,为企业物流运输管理提供了一种有效的包装优化思路和解决方法。
批量订单包装;物流箱;模拟退火算法;贪婪策略;规格优化问题
在敏捷制造下,产品的订单量与出货频次呈现差异化、高频率趋势[1],企业对产品物流箱通用性、标准化的要求越来越高,但在实际使用物流箱包装时,常会出现包装箱与产品尺寸适配度低的情况,导致包装材料的消耗量和运输体积增大,造成物流总成本增大。Lu等[2]研究发现,在现有解决方案中,消费者最倾向于通过优化包装策略解决过度包装问题。Geary等[3]和Ahire等[4]的研究均指出,正确的包装决策可以降低企业运营成本。由此可见,提高预制物流包装箱的通用性和标准化程度对降低企业产品包装成本、提高物流响应能力十分必要。
物流箱规格优化问题指根据待包装物的需求设计一个包含不同规格的物流箱型集合(文中用“物流箱型”表示),最终以最小成本包装全部物品。物流箱规格设计一般基于2种尺寸:运输工具尺寸、内装物尺寸。前者运用模数法,按照运输工具(托盘、集装箱等)尺寸组合分割得到物流箱尺寸[5-6],或基于最大物流箱尺寸设计一系列小规格物流箱尺寸,便于堆码储存[7]。随着内装物规格的增多和运输场景的多样化,基于内装物尺寸的物流箱型设计更加符合实际需求。Lee等[8]以箱内空间利用率最大化为优化目标,提出一种混合整数线性规划模型,以优化特定箱型的运输箱长度。近年来有学者开始使用启发式算法或元启发式算法求解多品种产品的包装规格优化问题。Singh等[9]通过聚类内装物尺寸使包装箱的种类减少,再以最小化运输成本为优化目标,采用遗传算法计算得到物流箱型,并分别用玩具、设备和医疗用品订单对算法可行性加以验证。丁奥等[10]以包装用纸箱耗纸量最少为优化目标,通过重新定义人工鱼群含义和求解策略,使用改进人工鱼群算法求解快递箱规格优化问题。此外,在研究包装箱优化等相关问题时,学者们还将空间利用率[11]、运输燃料费[12]等作为优化目标。
在待包装物体积较大时,1个箱子无法装下,还需考虑将待包装物体拆分后再装箱的问题。可拆分对象的装箱问题(Fragmentable Object Bin Packing Problem,FOBPP)最早由Mandal等[13]提出,指在不超过被包装物的最大可拆分数量和容器体积的情况下,将待包装物拆分成多个对象,并用不同容器包装的装箱问题。后有许多学者对模型进行了细化和扩充,Castro-Silva等[14]引入了负载平衡约束,求解同一规格容器中分装等量物品问题;Wei等[15]在研究选箱及装箱问题时,设计了一种二进制搜索方法,避免在枚举装箱策略时花费过多的计算时间。
针对以批量订单为包装对象的物流箱规格优化问题的研究尚较少,该问题不仅要考虑物流箱规格优化问题,还需考虑物流箱尺寸变化时的批量订单最优装箱问题,该问题具有一定的复杂性和求解难度。由此,文中针对面向包装多型号、多批量产品的物流箱规格优化问题,以产品订单内容为待包装物,构建一种订单分包规则,以包装材料总成本最小化为目标建立优化模型,提出一种包含贪婪策略的改进模拟退火算法求解该模型。
1 问题描述
针对大型仓储包装及物流需求,预制一系列不同规格的纸箱,以随时满足所有下达订单的包装需求,并实现降本。其中,下达订单中涉及的产品型号和数量繁多,通过尺寸不一的矩形块来表征不同型号的产品。由此,将此问题抽象为:在满足包装需求的前提下,确定1个物流箱型集包装1批订单,使包装成本最小。其中,物流箱与每个订单之间必须满足以下4个基本约束条件。
1)订单在装箱时产品之间无缝隙。
2)1个物流箱内放置的产品总体积不能超过该箱型的容量。
3)每个订单最多使用2种物流箱型包装。
4)订单之间不存在混装情况,即1个物流箱内仅包含1个订单的部分或全部内容。
在满足上述4个约束条件的基础上,在打包时尽可能地优化订单,并接近真实的人工打包习惯和效果,优化及打包策略主要考虑了以下几方面。
1)按订单打包时,除考虑物流箱成本外,还需考虑其他包装材料的成本,如缓冲衬垫、透明胶带等。
2)按订单打包时,筛选出多个满足条件的物流箱型,并遵循空间利用率最大原则,选出最适配的包装方式。
3)对于体量较大的订单,需要拆分打包,在分包时尽可能多地利用物流箱内的容积,使运输效益最大化,即考虑可拆分对象装箱模型的实际应用。
2 物流箱规格优化模型
不同订单的产品型号和数量各不相同,若1个订单内包含产品的数量过大,则全部装入1个物流箱内会导致包装件超重。由此,需制定一种订单分包规则,将订单合理分包后再对其包装规格进行优化。
对涉及的集合和符号进行说明:产品集合为,p表示集合中的第种产品,p∈,∈{1, 2, … ,p},产品p为尺寸各异的矩形块,长度、宽度、高度分别用l、w、h表示,质量为m,体积为V。输入订单集合为,o为集合中的第个订单,o∈,∈{1, 2, … ,o}。物流箱型集合为,c为集合中第种物流箱型,c∈,∈{1, 2, … ,c},物流箱型c的体积为V,长度、宽度、高度分别为l、w、h,并规定其最大和最小的长度、宽度、高度分别是max、max、max和min、min、min。
2.1 制定订单分包规则
首先,需确定产品p在物流箱型c中的最大装箱量n。因为同种产品之间的排列属于弱异构体排列,宜使用简单块的排列原则[16],以求得最大的装箱量,即沿同方向排列枚举出所有排列方式后求得。经计算后,得到集合中每种产品p在物流箱型c中的最大装箱量n,用于后续求解。
订单o中包含产品p的数量为q,引入决策变量x用于判断订单o中是否含有产品p,每笔订单中有且仅包含1种产品,用式(1)约束。制定订单分包规则:规定订单o最多使用2款物流箱型进行分包,2款物流箱型分别称为主箱型和零头箱型,用1和2表示。主箱型指包装o主要使用的物流箱型,产品p在主箱型中的装箱量必须达到n,否则使用零头箱型。零头箱指产品p使用该款物流箱装箱但装箱量小于其最大装箱量n的物流箱,其装箱量由该订单中未包装的产品数量决定。1的使用数量用n表示,为大于0的整数。2的使用数量用m表示,取值为0或1,0表示不使用零头箱,即使用一定数量的1包装o能恰好容纳q数量的产品p;1表示使用零头箱,由式(2)约束。包装每个订单使用主箱和零头箱数量的总和即为每个订单使用的物流箱总数量N,由式(3)表示。
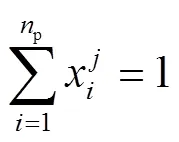

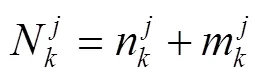
除尺寸约束外,在分包时必须小于物流箱可承担的最大装箱质量max,满足约束式(4)。在同时满足尺寸和质量约束的情况下,输出订单o所有可行的分包方案及包装订单o后物流箱箱内剩余空间总和Vrest通过式(5)计算。

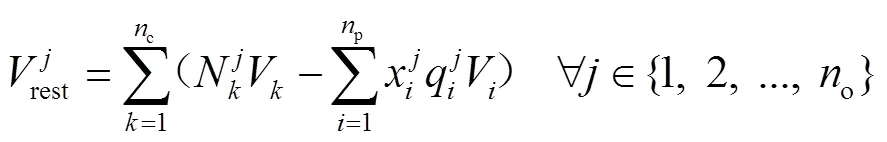
2.2 设定目标函数
根据上述模型确定订单分包方案,并将其作为包装对象,在物流箱型集合中使用适配规格和数量的物流箱打包。在装箱后,若箱体内部仍有空隙,则使用缓冲包装填充,最后使用胶带封箱。由此可见,选用的物流箱型与被包装物的适配程度直接影响包装材料的成本。当物流箱型与被包装物的适配度不高时,包装箱内的剩余空间较大,包装材料用量的增加会导致其成本升高。此模型使用包装材料的总成本作为评价物流箱型集合优劣的依据,并以包装所有订单使用的最小包装材料总成本作为目标函数。
订单的包装材料成本由3个部分构成,分别是物流箱成本carton、封箱胶带成本tape和缓冲衬垫成本buffer,通过式(6)计算。其中,物流箱材料使用瓦楞纸板,考虑到采购、库存成本等因素,根据对应箱型的使用数量制定价格梯度。将瓦楞纸板材料单价carton分为高、中、低3个梯度,并设置每款瓦楞纸箱的使用数量界限1和2,当使用数量小于1时使用高单价策略carton1,在1和2之间时使用中单价策略carton2,大于2时使用低单价策略carton3。物流箱成本carton通过瓦楞纸板单价与耗纸量的乘积计算,见式(7)。物流箱型c的耗纸量S由式(8)确定。封箱胶带成本的计算见式(9),在封箱时胶袋的截取长度超出物流箱长度尺寸部分用'表示,tape为胶带单价。式(10)用于计算缓冲衬垫的成本。由于缓冲填充物在箱体中填充体积与实际使用量相比有一定膨胀,取为膨胀系数的倒数,用于计算缓冲物的实际使用量,单价用buffer表示。


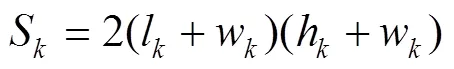

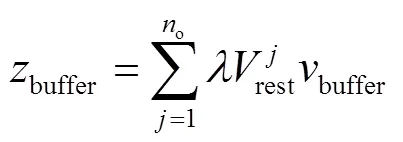
3 算法设计
这里求解的箱型规格优化问题已被证明属于NP-hard问题[16],针对该类问题常用元启发式算法求解,如遗传算法、模拟退火算法、人工鱼群算法等。模拟退火算法(Simulated Annealing Algorithm,SA)通过模拟热力学中的退火过程,由某个较高温度开始,随着温度缓慢下降不断重复搜索优解,直到满足终止条件。SA的优点是在算法初期可以搜索更广泛的解空间,通过扩大搜索范围,或根据Metropolis准则以一定概率接受差解,以避免算法陷入局部最优。SA算法的计算流程简单且通用性较强,这里拟采用此算法进行求解。由于SA算法存在对整体解空间认识不足、搜寻效率较低、所求解性能有限等问题,因此这里提出一种改进SA算法求解。即,在生成初始解阶段,将解均匀分布在可行域中,避免陷入局部求解;在解探索阶段,设计一种新型解更新算子提高算法寻优能力,设计一种自适应步长策略平衡算法前期全局搜索能力和后期局部搜索能力;提出一种有效的处理方式,以处理求解过程中出现的无效解情况。
此外,解的变化使参数的多样性增加,大大提高了计算的复杂程度,会影响后续目标函数值的计算效率。贪婪算法具有自顶向下的处理方式,在求解问题时将问题简化为若干个子问题,以求得最优解,经过多次贪婪选择后最终得到整体的最优解。这里采用引入贪婪分包策略的改进模拟退火算法求解物流箱规格优化问题,算法流程如图1所示,算法步骤如下。
1)初始化参数。确定退火初始温度0、终止温度min、退火系数、马尔可夫链长、最大可重复搜索次数max、步长step等参数及初始解状态0。
2)通过位置更新算子生成新解集s,并由贪婪分包策略确定订单分包方案,计算目标函数(s)。
3)判断当前解集是否为无效解。若不是无效解,则进入步骤4;否则,判断重复搜索次数是否小于最大重复搜索次数max。若小于max,则跳转至步骤2);否则跳转至步骤6)。
4)判断当前解s的目标函数(s)是否小于当前最优解(*),或满足Metropolis准则。若是,则更新当前解为当前最优解,否则跳转至步骤5)。
5)判断当前链长是否小于马尔可夫链长。若是,则返回步骤2),否则跳转至步骤6)。
6)判断当前退火温度T是否大于等于最小退火温度min。若是,则利用退火系数更新退火温度,并计算自适应步长step,跳转至步骤2)。若否,则终止算法。
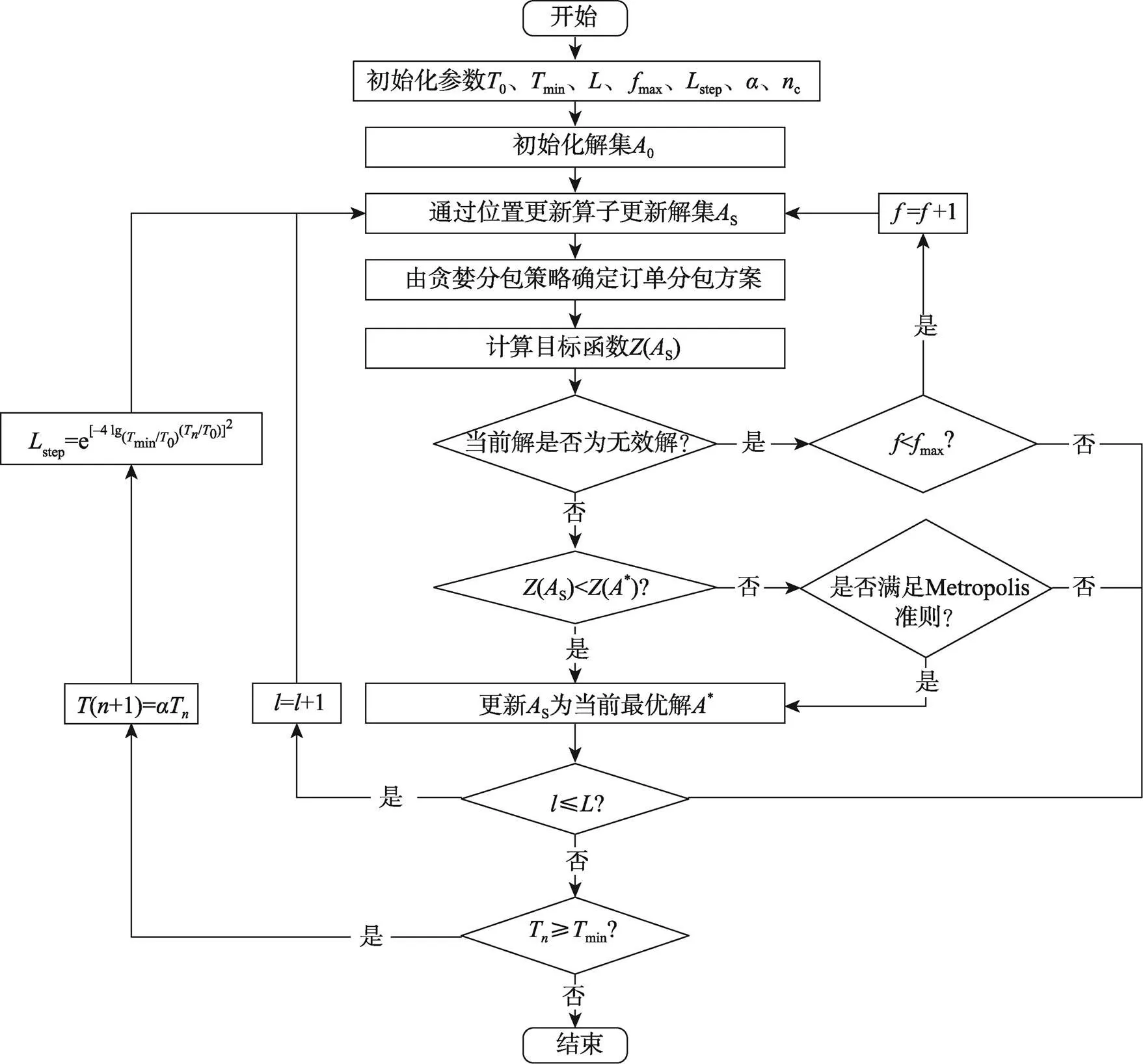
图1 算法流程
3.1 解的表示
此算法的解由物流箱型集合中不同的物流箱型构成,由矩阵s表示,如式(11)所示。其中,每个行向量表示1款物流箱型,行向量中的3个元素分别表示该款物流箱型的长度、宽度、高度,集合中共包含的箱型数量c对应矩阵的行数。将解的最大和最小边界max=(max,max,max)和min=(min,min,min)作为解搜索的可行域,生成的所有解均要求在可行域内。

3.2 解的初始化
初始解在一定程度上决定了后续优化方向,合理的初始化解方法对于算法求解至关重要。为了使搜索范围在可行域内分布得更广,采用Δ、Δ、Δ分别表示物流箱各方向最大与最小尺寸的差值,通过式(12)得到初始解0,使初始解均匀分布在可行域中。
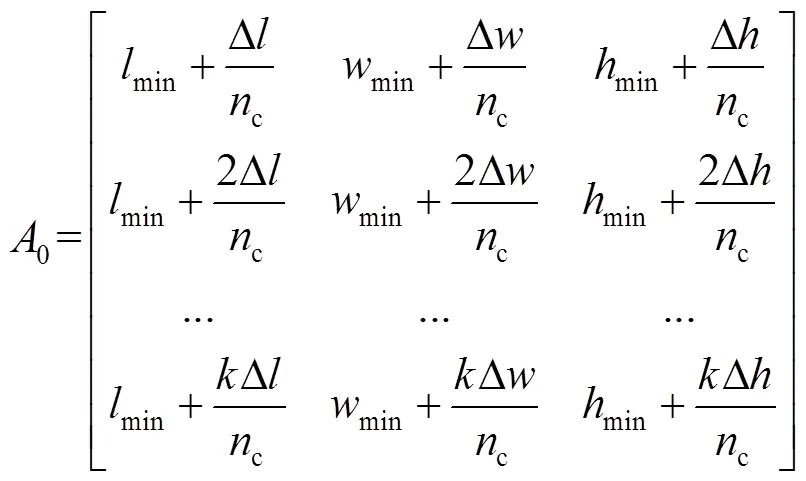
3.3 基于贪婪策略确定订单分包方案
贪婪算法的核心是选择一种合适的贪婪策略,得到满足一定条件的最优解。由此,基于贪婪策略求解订单最优的分包方案,以包装所有订单使用的物流箱内剩余空间总和最小为目标函数确定订单的分包方案,将其作为待包装物参数,用于后续目标函数的计算,可以提高算法整体的求解效率。贪婪策略的目标函数如式(13)所示。

基于贪婪策略确定最优订单分包方案步骤如下。
1)产品最大装箱量初始化。以当前解s为研究对象,计算每种产品在每种物流箱型中的最大装箱量。
2)得到所有可行的分包方案。订单按照分包规则逐一使用每款物流箱型作为主箱型进行分包,输出每个订单满足约束的所有分包方案。
3)求解最优分包方案。以式(13)为目标,求得每个订单的最优分包方案,并将其作为本代改进SA算法求解时的参数。
3.4 无效解处理机制
无效解指当前订单中的产品无法放入现有集合的任何一款物流箱型中,则称该物流箱型集构成的解为无效解。针对该情况,此算法设置了最大可重复搜索次数max,当出现无效解时,在本代重新搜索可行解,将搜索次数记为。若执行max后仍无法得到本代的可行解,则不更新本代解。
3.5 解的接受准则
接受准则是在迭代过程中如果当前适应度值优于目前优解*,则接受新解,接受概率为1;否则采用Metropolis接受准则以一定概率接受差解,以便后续在新邻域中重新寻优可行解,从而避免解陷入局部最优。接受概率由式(14)表示。此外,差解接受概率随着退火温度的降低而逐渐减小,最终趋于0。
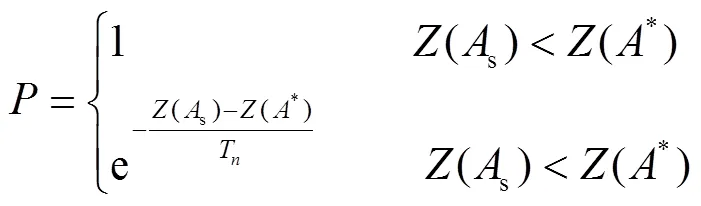
3.6 迭代准则
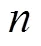
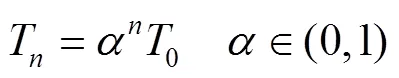
3.7 自适应步长策略
在解搜索过程中,步长越大,越容易进行全局搜索,但降低了搜索精度;反之,步长越小,求解精度越高,但易陷入局部最优。此算法提出了一种自适应步长策略,如式(16)所示。该自适应步长综合考虑了退火的初始温度、终止温度和当前退火温度的关系,使步长随着退火温度的变化而改变。在算法初期退火温度较高时,较大的步长可以扩大解搜索范围,使解搜索空间更全面,避免陷入局部最优;随着退火温度的降低,自适应步长逐渐变小,在局部范围内更易搜索到优解。

3.8 解位置更新算子
原SA算法解的更新是解在定步长内随机变化,因此解搜索能力不足。这里引入向历史最优解靠拢的思想,根据当前解s和历史最优解*中每款箱型的位置关系更新解邻域搜索范围。变量d为s中某元素a和*中对应位置元素a之间的距离,通过式(17)表示。其中,角标表示解矩阵的第列。新解位置的搜索范围由当前解位置、步长step、距离d,以及解的最大边界和最小边界max、min确定,分别用+和−表示当前解位置上对应元素与步长之间的和或差值,新解取阈值内随机整数更新解中各元素,如式(18)所示。比如,当距离大于0时,当前解为邻域搜索范围的最小值,搜索范围的最大值取当前解位置与步长之和、当前解位置与距离之和、解的最大搜索范围这三者中的最小值。
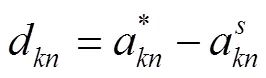

4 实例分析
为了验证算法的效果和可行性,运用实例进行仿真试验。A企业是一家全球性半导体制造商,主销产品是各类芯片,产品形态为多个芯片集成后构成的不同规格矩形块。使用A公司2021年某季度销售的39 321条订单数据进行算例分析,采集的订单数据中共包含612种产品,不同型号产品的长度、宽度、高度分别为188~588 mm、79~355 mm、20~105 mm,单笔订单内包含产品的数量为1~280个。为了增加对比性,分别比较了改进SA算法与其他算法的效果,并与企业现行物流箱方案进行对比,证明算法的有效性。此外,探究了不同物流箱型数量对使用包装材料总成本的影响,将c取5~20进行计算分析。本文算法使用Python开发,所得结果均在AMD Ryzen7 4800H-2.90 GHz CPU、Windows 64位操作系统的PC上得到。
模型参数设置:物流箱型的最大规格,max=650 mm,max=650 mm,max=450 mm;单箱可承载的最大装箱质量max=20 kg,物流箱型数量c=9;在包装材料定价方面,使用数量界限1=1 000个,2=10 000个,物流箱单价分别为carton1=6.54 元/m2,carton2=5.04元/m2,carton3=4.68 元/m2,胶带定价tape=0.05 元/m2,缓冲材料定价buffer=53 元/m2;其他参数,'=280 mm,=1.5。在模拟退火算法中,初始温度、退火系数和终止温度共同影响外循环的迭代次数,迭代次数越多则搜索越充分,但过长的迭代次数会导致搜索时间过长且无效搜索次数增多;采用马尔可夫链长控制内循环次数,过短导致搜索不充分,过长则会导致搜索时间大大增加。由此,综合考虑了计算效果和求解时间,将算法参数设置为初始温度0=100 000 ℃,终止温度min=1 ℃,初始步长step=100,退火系数=0.95,马尔可夫链长=25,最大重复搜索次数max=10。
4.1 算法分析
将文中的改进SA算法与原SA算法,以及加入文中解位置更新算子的原SA算法和加入文中自适应步长的原SA算法的求解情况进行了比较,算法迭代图如图2所示。原SA算法的初期解探索能力较差,在迭代中后期陷入局部最优,求解能力有限;在加入文中解位置更新算子后,算法在全局搜索方面更具优势,提高了原SA算法的寻优能力;加入文中自适应步长策略的原SA算法,在算法中后期有更强的局部搜索能力。文中SA算法结合了2种策略,其最优解的求解能力较原SA算法提升了15%,得到了更优解。
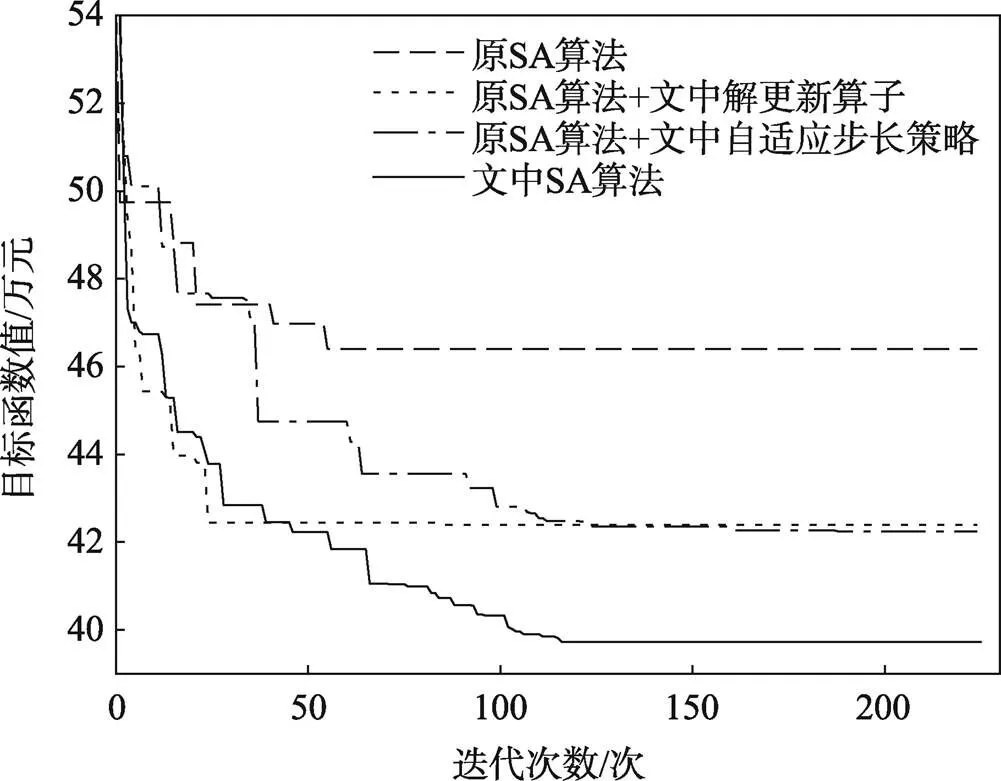
图2 改进SA算法分析
4.2 算法评价
为了评价文中算法,将文中SA算法与文献[11]中的改进人工鱼群算法(AFSA)、文献[16]中的改进遗传算法(GA)进行了性能对比,算法迭代对比如图3所示。其中,AFSA算法的种群规模为9(与物流箱型数量相同),视野为100 mm,觅食次数为15次,退火冷却系数为0.95;GA算法中的种群规模为30,采用锦标赛选择算子、交叉算子和随机变异算子,交叉概率为80%,变异概率为40%。为了更好地对比算法效果,2个算法的目标函数和迭代次数均与文中算法一致,其他条件保持不变。
由图3可知,文中SA算法在整个迭代过程中的表现均优于文献[16];与文献[11]相比,在迭代初期文中算法会出现目标函数值略低的情况,但在迭代中后期文中算法表现突出。算法分析:文中改进SA算法使用解更新算子,相较于文献[16]采用锦标赛选择算子和交叉算子,有较优的算法寻优效率,使得整个迭代过程的每代解均优于文献[16]。文献[11]通过自定义人工鱼群,使得迭代初期的结果较优,但算法在后期缺乏对解的持续探索能力。文中改进SA算法通过加入自适应步长策略,平衡了前期全局搜索能力与中后期迭代的持续探索能力,得到了更优解。可以证明文中SA算法具有更优的解探索能力,并可得到最优解。
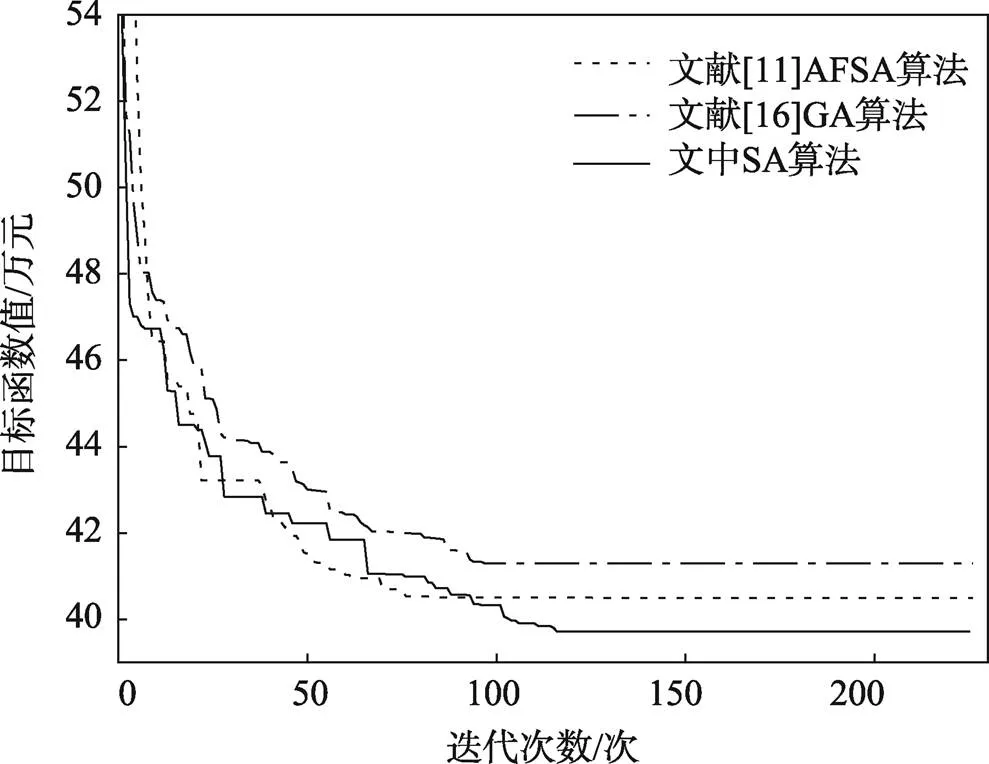
图3 算法迭代对比
当物流箱型数量c设置为9时(与企业现行物流箱型数量一致),与A企业现行箱型相比,包装算例订单所用包装的总成本为39.72万元,总耗纸量为77 640 m2,箱内空间利用率为71.61%。与A企业包装现状相比,其总成本降低了17%,总耗纸量减少了17%,箱内空间利用率提高了8%,具体数据对比见表1。由此可见,企业在使用优化后的物流箱型包装批量产品时,可实现降低包装材料总成本的目的,在节约包装材料、提高装箱空间利用率的同时,减少了企业运营成本。
表1 物流箱规格优化情况对比

Tab.1 Comparison of logistics bin specification optimization
4.3 箱型数量与成本关系
通过分析不同数量规格的物流箱型对包装材料总成本的影响,为企业管理者制定物流箱型数量提供了思路和依据。按照现有成本模型计算物流箱型数量与包装材料总成本的关系,结果如图4所示。由图4可知,当物流箱型数量为5种时,所用的包装材料总成本最高为42.13万元;当物流箱型数量为14种时,所用的包装材料总成本最低,为38.68万元。由此可知,制定14种箱型数量构成该仓储物流环境下预制物流箱规格集时可使包装材料的总成本最小。
总体来看,包装材料总成本随着物流箱型数量的增加,呈现先迅速减小后缓慢增大的趋势。在物流箱型的数量小于14种时,包装材料总成本随着物流箱型数量的增加而减少。当物流箱型的数量大于14种时,包装材料总成本随着箱型数量的增加而缓慢增加。出现这个趋势的原因,一方面,在箱型数量较少时,随着物流箱型数量的增加,瓦楞纸板材料的耗纸量降低,且纸箱内空间的利用率增加;另一方面,在箱型较少时,每款箱型的使用数量均较多,瓦楞纸板材料多为中低定价,因此包装材料总成本在该区间内急速下降。当物流箱型的数量超过一定值时,由于箱型数量的增加使得大部分物流箱型采用高定价策略计算物流箱成本。另外,箱型数量的增多提高了物流箱与产品的适配度,使得包装材料用量更合理,因此包装材料的总成本缓慢上升。
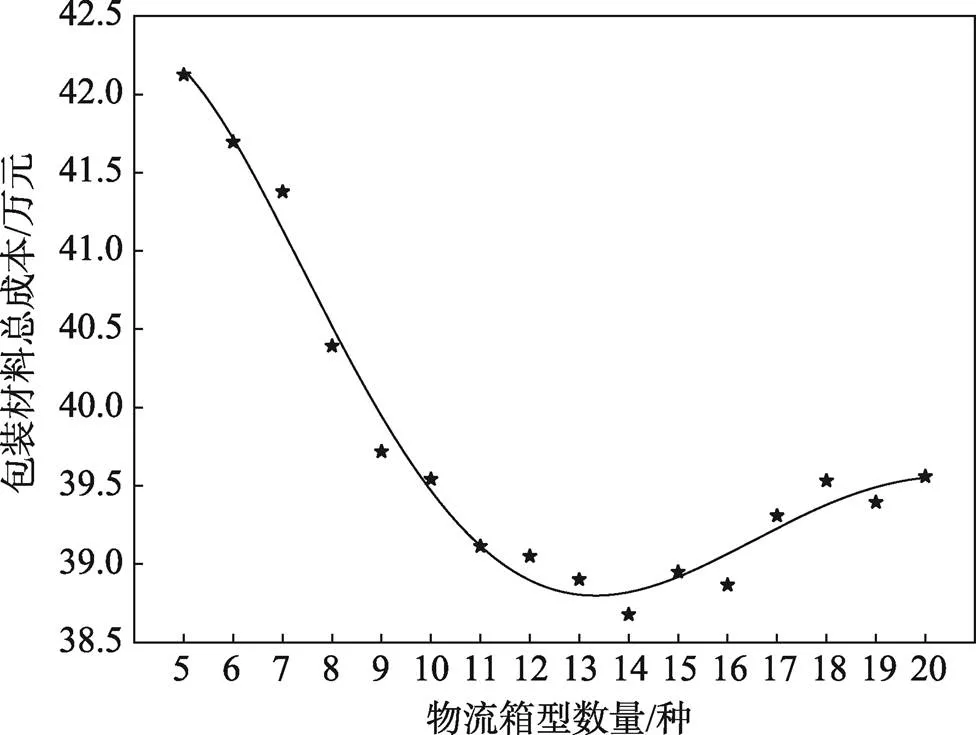
图4 物流箱型数量与包装材料成本之间的关系
5 结语
为了提高物流包装通用性,满足标准化需求,针对多型号、多批量的物流箱规格优化问题,通过建立订单分包规则得到符合约束的分包方案,综合考虑包装材料用量、箱内空间利用率等因素,以包装材料总成本最小化为目标建立优化模型,并提出了使用贪婪分包策略的改进SA算法求解该模型。贪婪分包策略用于求解订单的最优分包方案,改进SA算法提出了一种解位置更新算子和自适应步长策略,以提高算法搜索能力,并提出一种无效解处理机制。使用企业实例进行验证,通过与其他文献中算法进行比较,证明文中算法有效,并分析了物流箱型数量与包装材料成本之间的关系。
文中提出的方法可应用于多型号多批量产品或有订单分包需求的物流箱规格优化等方面,为后续相关研究及企业仓储管理提供了一种包装设计思路和解决方法,对降低企业运营成本具有一定参考意义。未来可考虑在运费成本、库存成本等多目标下对物流箱规格进行优化。
[1] BOYSEN N, DE KOSTER R, WEIDINGER F. Warehousing in the E-Commerce Era: A Survey[J]. European Journal of Operational Research, 2019, 277(2): 396-411.
[2] LU S, YANG L, LIU W, et al. User Preference for Electronic Commerce Overpackaging Solutions: Implications for Cleaner Production[J]. Journal of Cleaner Production, 2020, 258: 120936.
[3] GEARY S, DISNEY S M, TOWILL D R. On Bullwhip in Supply Chains—Historical Review, Present Practice and Expected Future Impact[J]. International Journal of Production Economics, 2006, 101(1): 2-18.
[4] AHIRE S L, MALHOTRA M K, JENSEN J B. Carton-Mix Optimization for Walmart.com Distribution Centers[J]. Interfaces, 2015, 45(4): 341-357.
[5] 李梦迪. 某企业产品物流包装尺寸标准化及装箱优化研究[D]. 南京: 南京大学, 2020: 12-15.
LI Meng-di. Research on the Standardization of Logistics Package Size and the Optimization of Loading of a Company's Products - Taking Company Z as an Example[D]. Nanjing: Nanjing University, 2020: 12-15.
[6] 左新宇, 张晋姝. 供应链视角下的物流包装单元系统[J]. 供应链管理, 2021, 2(3): 105-117.
ZUO Xin-yu, ZHANG Jin-shu. Logistics Packaging Unit System from the Perspective of Supply Chain[J]. Supply Chain Mangement, 2021, 2(3): 105-117.
[7] 徐丽, 周信冠彤, 刘心宇, 等. 低碳经济下绿色快递包装纸箱的模数化研究[J]. 包装工程, 2021, 42(23): 146-154.
XU Li, ZHOU Xin-guan-tong, LIU Xin-yu, et al. Modularization of Packaging Carton for Green Express under Low Carbon Economy[J]. Packaging Engineering, 2021, 42(23): 146-154.
[8] LEE S J, CHEW E P, LEE L H, et al. A Study on Crate Sizing Problems[J]. International Journal of Production Research, 2015, 53(11): 3341-353.
[9] SINGH M, ARDJMAND E. Carton Set Optimization in E-commerce Warehouses: a Case Study[J]. Journal of Business Logistics, 2020, 41(3): 222-235.
[10] 丁奥, 张媛, 朱磊, 等. 基于人工鱼群和模拟退火算法的电商快递纸箱规格优化[J]. 包装工程, 2021, 42(13): 218-224.
DING Ou, ZHANG Yuan, ZHU Lei, et al. E-Commerce Express Carton Specification Optimization Based on Artificial Fish Swarm and Simulated Annealing Algorithm[J]. Packaging Engineering, 2021, 42(13): 218-224.
[11] 牟钧, 刘震, 时红林, 等. 汽车CKD零部件包装箱尺寸链设计及集装箱拼箱研究[J]. 汽车与驾驶维修(维修版), 2021(S1): 28-30.
MOU Jun, LIU Zhen, SHI Hong-lin. et al. Dimension Chain Design of CKD Parts Packing Box and Research on Container Merging[J]. Car and Driving Repair (Repair Edition), 2021(S1): 28-30.
[12] DAS J N, TIWARI M K, SINHA A K, et al. Integrated Warehouse Assignment and Carton Configuration Optimization Using Deep Clustering-Based Evolutionary Algorithms[J]. Expert Systems with Applications, 2023, 212: 118680.
[13] MANDAL C A, CHAKRABARTI P P, GHOSE S. Complexity of Fragmentable Object Bin Packing and an application[J]. Computers & Mathematics with Applications, 1998, 35(11): 91-97.
[14] CASTRO-SILVA D, GOURDIN E. A Study on Load-Balanced Variants of the Bin Packing Problem[J]. Discrete Applied Mathematics, 2019, 264: 4-14.
[15] WEI L, OON W-C, ZHU W, et al. A Goal-Driven Approach to the 2D Bin Packing and Variable-Sized Bin Packing Problems[J]. European Journal of Operational Research, 2013, 224(1): 110-121.
[16] 韩宇阳. 带二维装箱约束的需求可拆分多车型车辆路径问题研究[D]. 南京: 南京大学, 2021: 16-21.
HAN Yu-yang. Split Delivery Heterogeneous Fleet Vehicle Routing Problem with Two-Dimensional Loading Constraints[D]. Nanjing: Nanjing University, 2021: 16-21.
Optimization of Logistics Bin Specification for Batch Order Packaging
LIU Ya-zhen1,WANG Li-qiang1,2*
(1. School of Mechanical Engineering, Jiangnan University, Jiangsu Wuxi 214122, China; 2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment & Technology, Jiangsu Wuxi 214122, China)
The work aims to propose a prefabricated logistics bin specification optimization model and algorithm to solve the order packaging problem of multi-variety and multi-batch products in warehousing logistics environment. Firstly, the split packing rules were established for product orders to determine all split packaging plan. A logistics bin size optimization model was established with the minimum total cost of packaging materials for all orders as the optimization objective. Then, an improved simulated annealing algorithm was proposed for this model. After using greedy strategy to solve the optimal split packaging plan to reduce the computational complexity of the model, a new solution updating operator was designed to improve the optimization ability of the algorithm, and an adaptive step size strategy was designed to balance the global search and local search ability of the algorithm. The experimental results showed that the algorithm had stronger solving ability than other algorithms; compared with the packaging status of example enterprises, the same order could reduce 17% packaging cost. This method can be used to solve the problem of optimizing logistics bin specifications for series transportation under the application scenario of multiple product types, large size differences and dynamic updates, providing an effective set of packaging optimization ideas and solutions for enterprise logistics and transportation management.
batch order packaging; logistics bin; simulated annealing algorithm; greedy strategy; specification optimization problem
TB485.3;TP301.6
A
1001-3563(2023)17-0229-08
10.19554/j.cnki.1001-3563.2023.17.028
2023-01-04
中央高校基本科研业务费专项资金(JUSRP21115);江苏省食品先进制造装备技术重点实验室自主研究课题资助项目(FMZ201902)
责任编辑:彭颋

