大型钢管插入式基础裂缝产生机理及影响参数研究

孙雅珍,张 立,王金昌,程 尧,刘燕平

(1.沈阳建筑大学交通与测绘工程学院,辽宁 沈阳 110168;2.浙江大学交通工程研究所,浙江 杭州 310027;3.浙江华云电力工程设计咨询有限公司,浙江 杭州 310027)

人们生产和生活需求的不断增长,对电力能源的需求也越来越大,由此需要建设更多的高电压等级输电线路。相较于传统的基础型式,高电压等级输电线路对杆塔基础的要求更高。以大型型钢插入式混凝土为主的基础形式由于具有较高的工程性能得到了广泛应用。铁塔在风荷载等作用下,基础立柱易产生裂缝,导致构件耐久性减弱,进而极大地减少结构的使用寿命。大型型钢插入式基础可分为角钢插入式基础与钢管插入式基础。鲁先龙等[1]通过室内模拟试验和现场试验验证了角钢插入式基础结构的合理性,为工程应用提供了参考。郑勇等[2]将插入式钢管承压板锚固试验以及底板锚固试验结果与日本相关规范中的计算公式进行了对比,并对插入式钢管锚固设计提出了建议。在钢管插入式基础的设计中,钢管与混凝土的黏结、锚固性能,截面特性,以及钢管与基础主筋的应力特性是关键因素,其中钢管与混凝土间的界面黏结强度与混凝土的强度有关[3-4]。白亮[5]、明铭等[6]对型钢混凝土试件进行试验研究,建立不同状态下型钢混凝土黏结应力计算表达式,提出黏结应力-滑移本构关系,并采用非线性弹簧单元模拟型钢与混凝土界面间的黏结性能。童瑞铭等[7]针对现行规范中输电线路杆塔基础配筋率以及位置系数取值不明确等问题进行了现场试验研究,提出了基础配筋以及基础尺寸的设计方法。高志林等[8]采用有限元方法对复杂荷载工况下钢管插入式基础进行研究,探讨了其设计计算过程的关键因素。

上述研究多针对插入式基础的承载能力与受力机制,对其裂缝控制方面的研究较少,且现行设计一般只做均布荷载下的裂缝验算。由此,笔者根据童瑞铭等[7]的试验数据,基于内聚力模型,结合扩展有限元方法建立三维实体模型,通过将数值结果与试验结果对比验证有限元计算模型的有效性与准确性。在此基础上,建立大型钢管插入式基础模型,分析了单、双锚板钢管插入式基础在不同配筋方案、不同位置系数情况下承受上拔力作用时的裂缝扩展情况;对比基础开裂密度与应力强度因子,并总结得出合适的配筋方案及位置系数取值,以期为大型钢管插入式基础的设计提供参考。

1 有限元模型建立

1.1 扩展有限元基本原理

扩展有限元(XFEM)基于单位分解理论,在传统有限元法的位移函数上增加富集项[9],即采用对裂缝附近单元的节点自由度加强,来描述裂缝的不连续性,通过添加水平集函数的方法来表征裂缝界面,此外,在网格划分方面,不需要对裂缝尖端网格加密或引入奇异单元,使用常规单元进行网格划分即可。

传统有限元法的单元内任意一点的位移函数表示为

(1)

扩展有限元下的位移函数为

(2)

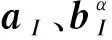
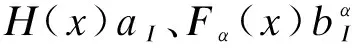
(3)

式中:x为高斯点;x*是裂缝上距离x最近的点。

裂缝尖端坐标系如图1所示。

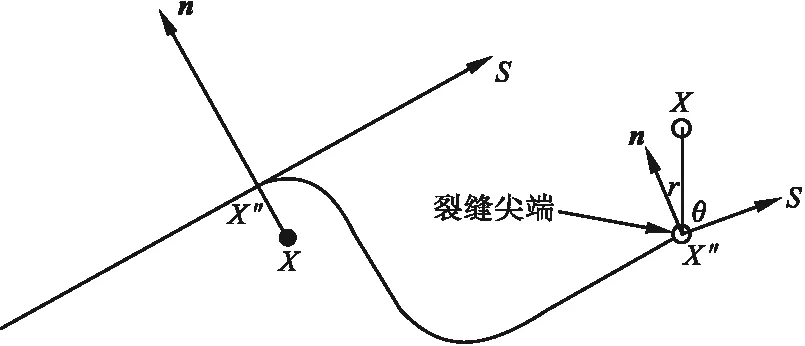
图1 裂缝尖端坐标系Fig.1 Crack-tip coordinate system

n为裂缝在x*处的法向量,若x在裂缝面法线指向的一侧,H(x)取1;反之,则H(x)取-1。Fα(x)为裂缝尖端渐进函数,该函数由四个基函数组成,可以描述裂缝尖端的不连续性,在局部坐标系下的表达式为

(4)

1.2 内聚力模型

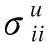
图2 内聚应力-相对位移关系Fig.2 Cohesive stress-relative displacement relationship

内聚力单元的三个方向之间是相互独立的,计算其中某一个方向时,可以不考虑另外两个方向的影响,其应力应变本构关系为

(5)

式中:Knn为法向刚度;Kss、Ktt为两个正交的切向刚度;δn、δs、δt分别对应为法向位移和两个切线位移;To为内聚力单元厚度。

内聚力模型设置了界面单元进入初始损伤的判断依据,选择一次应力准则来计算界面单元在复合条件下的初始损伤条件:

(6)

2 有限元模型验证

2.1 构件有限元模型

按照文献[7]的试件尺寸建立有限元模型,混凝土立柱截面为900 mm×900 mm,钢管规格为219 mm×10 mm,插入深度为1 533 mm;锚板宽×厚为120 mm×20 mm,锚板锚固深度为600 mm;纵向钢筋配置为20Φ20。根据试件尺寸建立等比例模型,根据对称性原理,有限元计算模型取1/4模型。混凝土立柱、钢管和承载板均为三维实体,单元类型为C3D8R(见图3)。

图3 有限元模型Fig.3 Finite element model

模型边界条件根据1/4模型性质设置:混凝土立柱底部采用固定约束,侧面则根据对称性约束其法向位移。钢管与混凝土界面设置内聚力单元;纵向钢筋和箍筋均嵌入到混凝土中,与混凝土协同变形。钢管顶部施加向上(沿z轴正向)的位移荷载。

2.2 材料参数

混凝土强度等级为C25,轴心抗压强度平均值fcm=19.74 MPa,轴心抗拉强度平均值ftm=2.16 MPa,混凝土弹性模量E=2.8×104MPa,泊松比μ=0.167,断裂能GF=60 N/m。开裂判断选取最大主应力开裂准则:

(7)

钢材采用理想弹塑性模型。材料参数如表1所示。

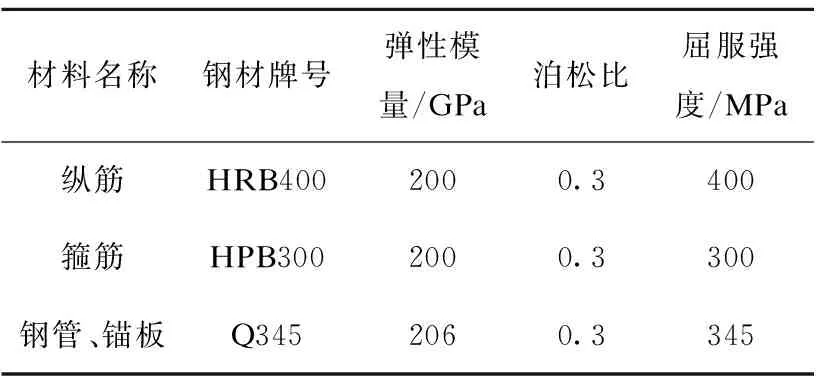
表1 材料参数Table 1 Material properties

2.3 有限元计算值与试验结果与对比

采用上述方法建立钢管插入式基础的有限元模型,计算得出的荷载—位移曲线与试验结果对比如图4所示。图4中,d为钢管上端沿受力方向的绝对位移值,F为作用在钢管上端的合力值。根据试验结果[7],试件破坏模式为钢管屈服,从试验曲线中可见试件的破坏荷载约为2 500 kN,有限元计算得出的极限荷载与试验结果接近,且在最大荷载时钢管进入塑性阶段。

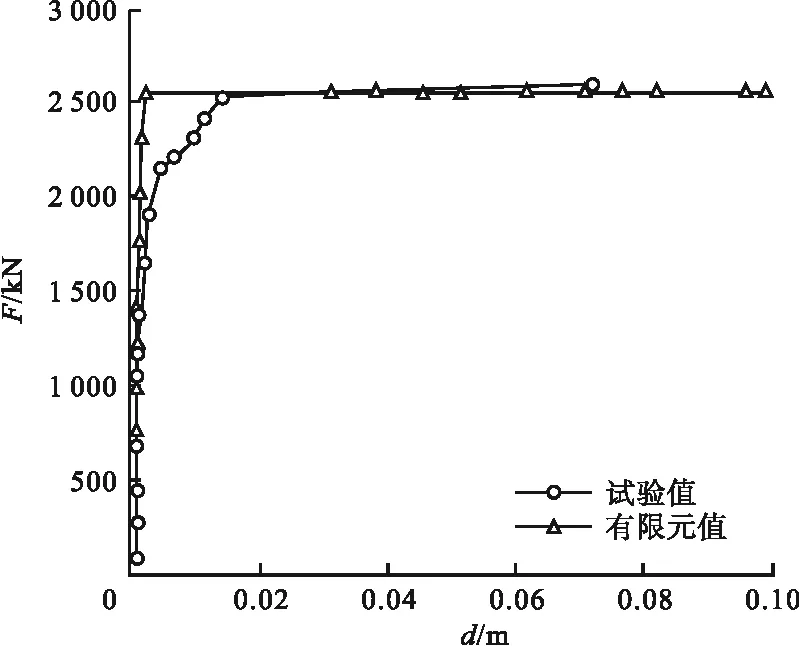
图4 构件有限元与试验F-d曲线对比Fig.4 Comparison of simulated F-d curve and measured curve

图5为有限元模型的裂缝分布云图和试件在极限荷载时的破坏形态。由于有限元模型中假设材料为各向同性,没有考虑骨料对裂缝的影响[12],所以裂缝基本从锚板位置向基础发展,与试验裂缝分布有一定差别,但总体上呈现出一致。因此,采用扩展有限元结合内聚力模型计算分析钢管插入式基础是可行的。

图5 裂缝分布情况对比Fig.5 Comparison of crack distribution

3 裂缝扩展机理与防裂控制

以某大型钢管插入式基础为例(见图6),钢管插入深度L为9 m,钢管直径D为1.0 m,壁厚22 mm。钢管插入式基础一般可设计为无锚板、单锚板、双锚板等类型。根据规范要求[11],a取最佳初始锚固位置1 m,b取双锚板的最佳间距0.8 m。为了研究不同锚固形式构件的裂缝扩展机理,通过建立上述3种钢管插入式基础有限元模型,分析其裂缝扩展情况。根据对称性,同样取1/4模型,材料参数与验证模型相同。

图6 钢管插入式基础结构图Fig.6 Structural design of steel-pipe-inserted foundation

3.1 基础构件裂缝扩展机理

图7～图9为通过有限元模拟计算得到的裂缝扩展云图,图中采用PHILSM(位移函数)描述裂缝面,函数值为零的表面为裂缝。由图7可知,无锚板基础由于钢管底部未采用锚固措施,上拔荷载直接传递到钢管底部,当钢管内部混凝土到达混凝土的开裂强度时,钢管内部混凝土与下部的混凝土产生脱开现象,因此无锚板构件开裂防治应注重钢管的底部锚固。由图8可知,增加单锚板设置能够明显提高钢管的锚固承载力,但是在荷载作用下锚板处与混凝土会产生较大的法向接触力,导致锚板处混凝土出现应力集中,进而产生裂缝,当锚板处裂缝扩展到基础表面时,接触应力向下传递。由图9可知,双锚板基础同样在锚板处混凝土首先出现裂缝,在第一块锚板处裂缝未扩展至基础表面时,接触传递的应力大部分由第一块锚板承担,因此第二块锚板处的裂缝扩展明显滞后于第一块锚板处。由于双锚板的存在,钢管的底部应力大大减小了,钢管锚固深度也可以相应减少,由此,对于采用锚板提高承载能力的构件,建议采用双锚板或多锚板,以防止基础底部开裂。

图7 无锚板基础裂缝扩展情况Fig.7 Crack propagation in non-anchored slab foundation

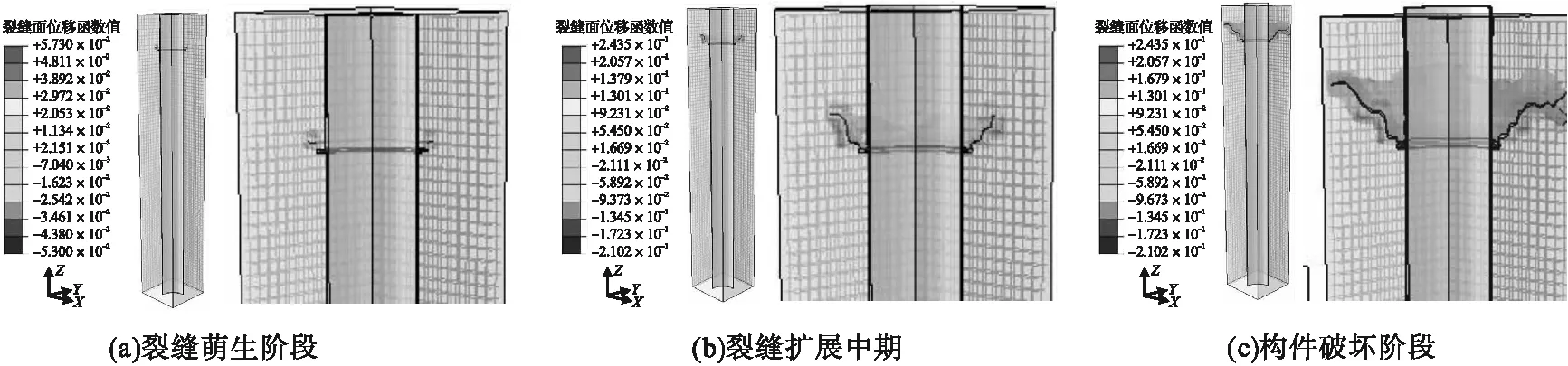
图8 单锚板基础裂缝扩展情况Fig.8 Crack propagation in single anchor slab foundation

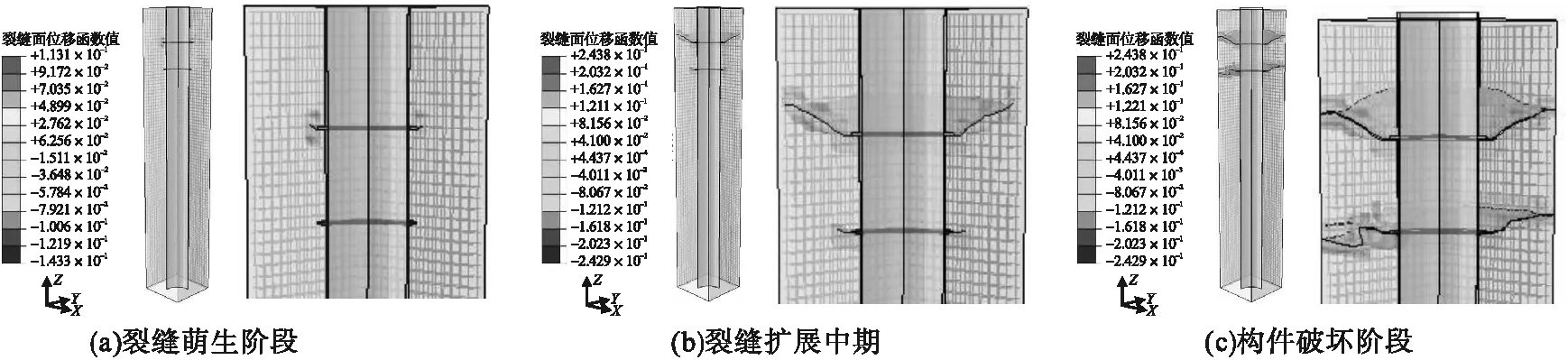
图9 双锚板基础裂缝扩展情况Fig.9 Crack propagation in double-anchor slab foundation

3.2 不同参数对裂缝的影响

除了锚固型式不同会影响钢管插入式基础裂缝扩展,基础配筋方式、配筋率以及位置系数也会对裂缝形成产生较大影响。

3.2.1 基础配筋率与配筋方式

假定基础、钢管尺寸不变,分别改变基础的配筋率和配筋方案进行有限元分析计算,对比不同配筋方案下基础裂缝扩展情况。配筋方案A为普通配筋,配筋方案B为在钢管外侧设置环状排列纵筋(见图10)。基于不同配筋率和配筋方式设置 6种工况,基础配筋情况见表2。

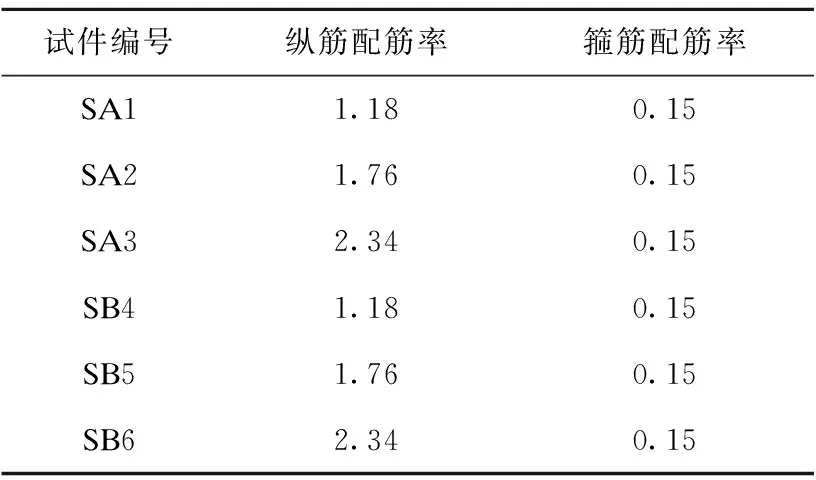
表2 基础配筋参数Table 2 Reinforcement of foundation %

图10 配筋方案Fig.10 Reinforcement pattern

ABAQUS扩展有限元法可以在计算过程中输出PHILSM和PSILSM,以表征裂缝状态,其中PHILSM表示指定的位移函数用于描述裂缝面,PSILSM描述初始裂缝朝向,并且裂尖不能停留在单元内,只能在边界上。由此设定以裂缝穿过的单元为开裂单元,通过计算得到开裂单元的体积,将单位体积基础内开裂单元的体积定义为裂缝密度[13]。不同配筋方案钢管插入式基础裂缝密度与钢管顶端位移d的变化关系如图11所示。

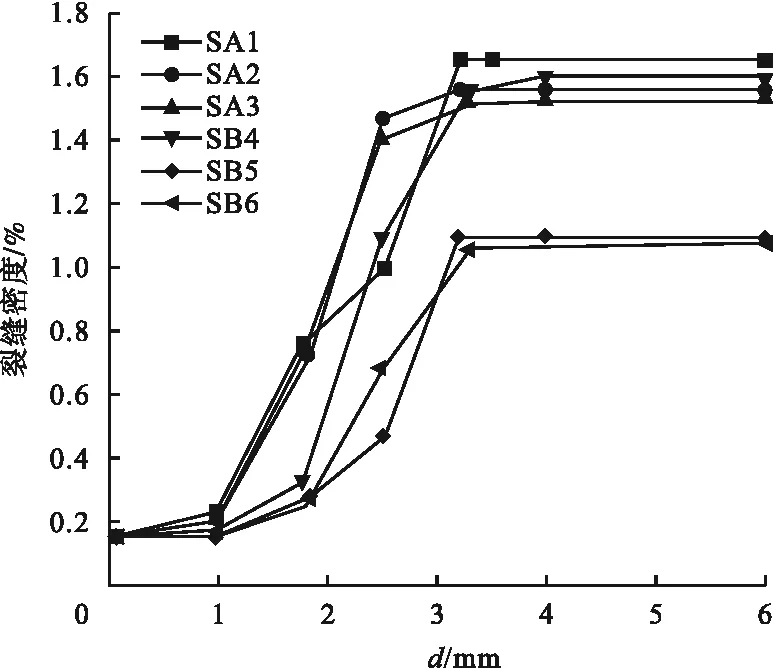
图11 裂缝密度变化曲线Fig.11 Fracture density curvess

由图11可知,对于配筋方案A,当基础配筋率由1.18%提高到2.34%,且钢管顶端位移小于2 mm时,由于基础裂缝先从锚板处混凝土开始发展,在较低荷载水平下,外围配筋不会对基础内部裂缝产生较大影响,因此在裂缝扩展初期A方案三种构件的裂缝密度相差不大。随着荷载水平的提高,具有高配筋率的SA2、SA3构件基础裂缝密度增长速度远远超过SA1构件,但最终构件破坏的时裂缝密度仍要小于SA1构件,这是由于基础外围的高配筋率使得外围混凝土抗拉承载力增强,进而限制裂缝向基础外侧扩展,由于裂缝不能继续往前扩展导致能量的积累,使得基础内部应力增加,从而使SA2、SA3构件在中后期裂缝密度增长速度加快。对于配筋方案B,由于钢管外侧设置的环状排列纵筋使得其在裂缝扩展前期的裂缝密度小于方案A。配筋率为1.18%时,由于方案B的前期裂缝扩展缓慢导致SB4构件在裂缝突破环状纵筋后能量迅速释放,使得裂缝密度增长速度要略大于方案A。当方案B配筋率大于1.76%时,由于第一块锚板处的裂缝并未突破环状纵筋使得裂缝密度远小于其他构件。此外,对比SB5、SB6构件可知,当方案B配筋率由1.76%提高到2.34%时,基础裂缝密度并没有减小,反而在裂缝扩展中段随配筋率提高而导致裂缝密度增大,因此,基础配筋率宜为1.76%。

3.2.2 位置系数

定义κ(κ=D/B)为内置锚固件圆钢管的混凝土基础钢管位置系数[14],位置系数反映了钢管截面与混凝土截面之间的比例关系。定义内置锚固件圆钢管的混凝土基础中钢管截面积与基础立柱截面积之比为配骨率γ:

(8)

式中:D为钢管直径;B为基础宽度;t钢管厚度。

钢管厚度相对于构件截面尺寸很小,即t/B为一相对小量,忽略此项造成的误差通常在2%～4%,且截面越大,误差越小。依据规范[15]在设计位置系数工况时必须满足圆钢管外径与壁厚之比D/t不应大于135×235/fy(fy为钢管屈服强度),钢骨钢管混凝土构件套箍系数设计值φ宜为 0.5～2.0,因此保持钢管直径不变,且各项参数满足规范要求,设置4种工况,具体参数如表3所示。

表3 基础位置系数参数Table 3 The parameters of position coefficient

由钢管插入式基础裂缝扩展机理可知,构件裂缝从锚板处开始萌生,因此在模型的锚板处预制裂缝,并限制裂缝扩展,用ABAQUS计算不同构件裂尖应力强度因子来描述弹性体裂尖部位应力场强弱程度[16],以此表征不同基础宽度构件的开裂趋势。采用应力强度因子为纵坐标、钢管顶部位移为横坐标绘制曲线(见图12)。由图可知,随位置系数的减小,构件应力强度因子呈现出不断减小的趋势,但是当位置系数低于0.33后,应力强度因子的减小幅度急剧变小,此后,再以减小位置系数来抑制基础开裂效果不佳,从而导致基础的经济性下降。

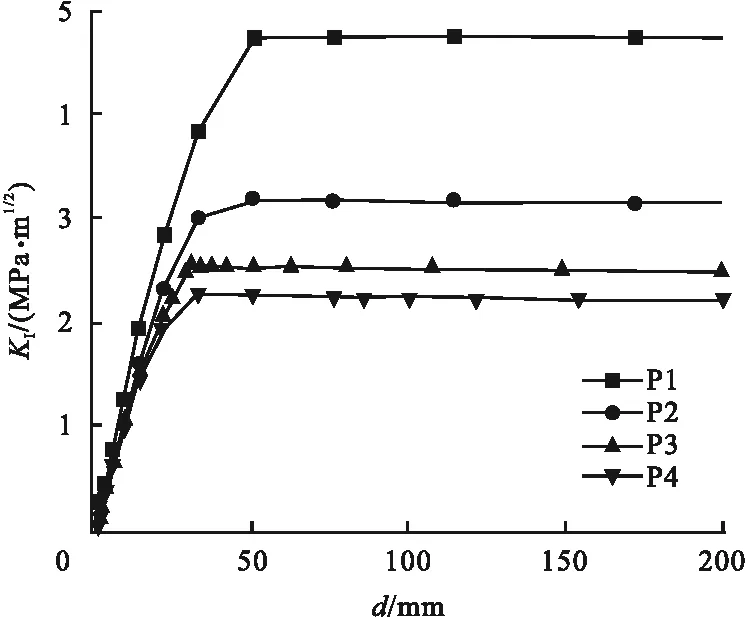
图12 应力强度因子变化曲线Fig.12 Stress intensity factors curves

通过对比不同位置系数构件裂缝密度变化曲线可知(见图13),随着位置系数的减小、钢管外侧混凝土的厚度增加使得构件裂缝密度在钢管位移小于1 mm时增长缓慢,与前述应力强度因子变化趋势类似,当位置系数小于0.33时,减小幅度趋于收敛。在钢管位移介于1～2 mm之间时,P3、P4构件的斜率基本一致,且基础裂缝密度相差较小,位置系数在0.33左右时构件结构较为合理。

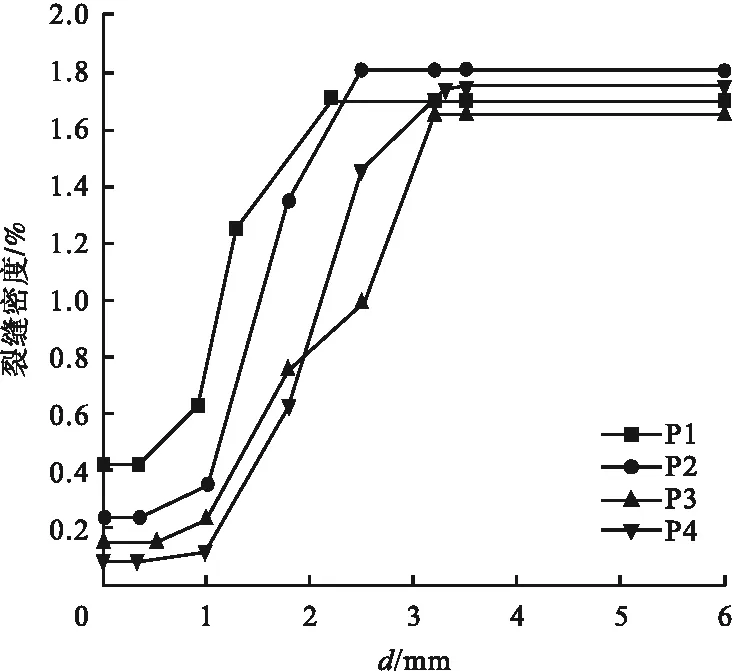
图13 裂缝密度变化曲线Fig.13 Fracture density curve

4 结 论

(1)对于无锚板构件开裂防治应注重钢管的底部锚固,对于采用锚板提高承载能力的构件建议采用双锚板或多锚板以防止基础底部开裂。

(2)采用在钢管外侧设置环状排列纵筋方式能够明显减小基础裂缝密度,当配筋率为1.76%时,构件能够抑制第一块锚板处的裂缝突破环状纵筋,且当配筋率再继续提高时会导致扩展中段裂缝密度增大。

(3)随着位置系数的减小,构件裂尖应力强度因子与基础裂缝密度呈现出不断减小的趋势,当位置系数低于0.33后,应力强度因子的减小幅度急剧变小,且裂缝密度相差不大,导致基础的经济性下降,从抑制裂缝开展角度考虑,位置系数在0.33左右时构件结构较为合理。