港口集装箱码头泊位与岸桥的多阶段协作调度仿真研究

冯小欧， 杨 瑾， 袁培燕

（1.郑州旅游职业学院，郑州 451464；2.河南师范大学计算机与信息工程学院，河南 新乡 453007）

0 引言

随着国际贸易的快速发展和大规模大吨位集装箱货柜船舶的发展趋势，集装箱码头的高效运营正面临巨大的挑战。集装箱船舶及其装卸设备也正在向着高速重负荷方向发展，这要求调度计划和集装箱码头作业不仅需要满足船舶的装卸工作任务要求，还要降低码头的作业代价和投资。集装箱码头的主要作业空间涉及两类主要资源：泊位和岸桥。泊位和岸桥是集装箱码头的稀缺资源，泊位分配和岸桥调度对于提高集装箱码头的运作效率至关重要。泊位分配是指为到港船舶安排靠泊位置和靠泊、离港时间，并最小化船舶在港时间。船舶等待靠泊时间最短、在港装卸作业时间最短、靠泊成本最低以及客户满意度最高为当今泊位分配的主要研究目标。依据码头作业时泊位分布方式的不同，可分为离散型泊位和连续型泊位。根据文献［1］中的表述，离散型泊位是将码头分割成一定数量的部分，每一部分即为一个泊位，在每一个时间点每一个泊位上只能停靠一艘船舶。而连续型泊位分布，码头没有被分割，在满足船舶长度的情况下船舶可停靠在码头边界的任意位置。连续型泊位相对离散型泊位能更好地利用空间，但连续型泊位分配较复杂。岸桥是集装箱码头重要的装卸资源，岸桥调度所要解决的是在给船舶分配好泊位后，根据到港船舶集装箱装卸任务量以及船舶离港时间等约束为船舶分配可用的岸桥。岸桥价格昂贵，如何减少岸桥的闲置时间，提高岸桥的利用率是集装箱码头取得竞争优势的关键。

泊位与岸桥协调调度比单独调度能更有效提高集装箱码头的装卸效率，减少船舶在港时间。图1 给出了泊位与岸桥单独调度和协调调度的作业流程。由于船舶停靠的泊位和泊位附近的岸桥工作状态不同，导致船舶的服务时间不同。泊位决策影响岸桥分配决策，从而影响船舶在港时间。协调调度在泊位调度时不仅要考虑泊位空闲情况，也要考虑该泊位可用岸桥的状态，计算停泊泊位岸桥的装卸时间，选择使船舶在港时间最短的泊位停靠。单独调度则将两个调度流程分开，先为船舶选择最短泊位停靠等待时间，停靠后再分配可用岸桥，后者忽视了岸桥分配对船舶在港时间的影响，造成后续船舶的等待，具有一定的局限性。协调调度避免了单独调度的局限性，可有效减少船舶总在港时间，并提高岸桥的装卸效率。

1 泊位与岸桥调度方式

为解决泊位和岸桥两类资源的调度，很多学者进行了研究。集装箱码头的泊位和岸桥分配的单独调度研究如文献［1-4］。基于静态调度和离散泊位调度的相关研究，文献［5］中提出一种动态调度方法，建立一种混合整数规划模型，其目标是最短化船舶的在港时间。文献［6］中提出连续泊位概念，此时泊位被视为连续空间，以最大化泊位的利用率。此外还将泊位转换为二维渐缩进行分析，结果表明，泊位调度是NPhard问题。为解决连续泊位分配，文献［7］中将要求的离港时间和在非最优泊位上的额外处理代价的总附加代价设置为最优化目标，并通过模拟退火算法时进行求解。基于以上的工作，文献［8］中通过分支界限法和自适应贪婪算法进行求解。文献［9］中提出一种多重任务调度模型，目标则是最短化最近船舶的离港时间，并提出一种启发式算法。类似内容还出现在文献［10］中。

为提高资源利用率，文献［11］中引入岸桥生产率到泊位和岸桥分配的协作调度。为最短化处理时间、等待时间和延时时间的总和，文献［12］中提出一种混合遗传算法对以上协作调度进行求解。由于码头工作的复杂性，连接泊位和岸桥分配的协作调度仍然缺乏有效的调度机制。文献［13］中为最短化船舶在港时间，提出免疫遗传算法的协作调度算法。文献［14］中将协作调度的优化目标设为最小化船舶在港时间和岸桥移动次数，提出泊位分配子模型和岸桥分配子模型的耦合模型，并采取一种嵌套循环进行算法进行求解。基于连接泊位的可分割性，本文提出一种最优化调度模型，模型利用多阶段启发式调度算法和粒子群优化算法（Particle Swarn Optimization，PSO）可有效处理在集装箱船舶动态调度中的协作调度。算法目标是决定船舶的泊位和泊位顺序以及岸桥的使用数量，以最小化优于非最优泊位带来的额外代价和停港延时的惩罚代价之和。

2 模型描述

船舶到港后的作业过程主要包括：船舶到港、分配靠泊位置（泊位）、分配岸桥、集装箱装卸以及船舶离港。为最短化船舶的总在港时间，码头管理者会根据到港船舶的相关信息以及码头装卸的优化策略，将最优的靠泊位置以及可用的岸桥分配给船舶装卸集装箱。

由文献［8］中可知，码头作业中，对于船舶而言有一个最优泊位，其装卸工作代价是最小的，（如邻近仓库位置，此时运输成本可以最小化）。对于泊位调度来说，船舶均想要优先选择这些泊位，若这些泊位不可用才考虑在次最优位置进行泊位。装卸作业时间取决于分配的岸桥数量。为确保船舶的离港时间和不必要的设备消耗，应该分理、正确配合岸桥数给船舶。因为岸桥数本身的限制，并不是所有船舶都能得到充足的岸桥数，尽量当船舶离港时，空闲岸桥需要重新分配给在港船舶，同时满足船舶对于岸桥的最大持有数，以便降低船舶的停留停港时间和延期带来的惩罚成本。

基于以上的分析，可通过离散化方法将连续泊位划分为一组序列组成的多个泊位，如图2 所示。船舶的最优泊位标识为分割后的序号，每个船舶可占用多个泊位段，但不能超过码头长度。同时，船舶的停靠位置可由船舶占用的泊位段进行标识。

模型相关符号说明

Q：岸桥数量集合｛1，2，…，q｝；

S：装载集装箱的船舶数量集合，S＝｛1，2，…，s｝；

L：泊位码头长度；

A：连续泊位分割量；

B：单个泊位的长度集｛1，2，…，L／A｝；

TEU：航线运输的集装箱标准箱；

M：岸桥效率，单位：TEU／h；

NCi：船舶i需要的最大岸桥数；

li：船舶i的长度；

Ci：港内船舶i的集装箱总量；

tpi：船舶i要求的离港时间；

tai：船舶i的到达时间；

bpi：船舶i的最优泊位，以bi表示；

Nhi：船舶i最右边的岸桥ID；

Nei：船舶i最左边的岸桥ID；

rpi：船舶i的实际泊位；

tbi：船舶i的泊位时间；

tdi：船舶i的实际离港时间；

WB：等待泊位的船舶集；

BW：作业过程中的船舶集；

OTS：延期船舶集；

addCranei：船舶i按时完成任务需要的额外岸桥数；

headCranei：处于泊位rpi左边的岸桥集；

endCranei：处于泊位rpi右边的岸桥集；

Ni：船舶i按时完成任务需要的岸桥数；

CSj：如果岸桥j正在作业，则CSj＝1，否则CSj＝0；

BSl：如果泊位段l正在作业，则BCl＝1，否则BSl＝0；

QCi：船舶i工作的岸桥集；

LCi：船舶i工作时的泊位集；

TLi：船舶i的左边集装箱数量；

tfi：船舶i的估计作业时间；

tyi：船舶i的估计离港时间；

nci：船舶i工作时的岸桥数；

wi：船舶i在港口中的等待时间；

thi：船舶i的作业持续时间。

船舶的操作时间主要由集装箱货柜车的运输时间和操作的岸桥数决定。船舶的停靠位置（泊位）可表示为运输时间。岸桥数量主要取决于要求的离港时间。本文应用文献［8］中提出的模型来求解这个调度问题。不同的是，两阶段的岸桥分配在泊位时进行了考虑。

式中：c1i为船舶在非最优泊位上的额外成本，cli为船舶i的单位额外成本；c2i（tdi-tpi）为船舶延期带来的惩罚成本；c2i为船舶i的单位惩罚成本。

3 多阶段协作调度

多阶段协作调度包括船舶泊位分配和岸桥分配，岸桥分配又划分为泊位时岸桥分配和离港后岸桥分配。

3.1 泊位分配算法

当船舶靠港时一般会选择最优泊位，即：船舶抵达港口后，首先检查最优泊位是否空闲，若空闲，则靠港泊位；若泊位已被占用，船舶选择次最优泊位；如果所有泊位均无法使用，船舶将被推迟进港，等待在锚泊区域。对已经泊位的船舶，离其最近的岸桥按船舶离港时间、处理集装箱数量和最大岸桥数量予以分配。泊位分配算法（Berth Allocation，BA）流程如图3 所示。

3.2 岸桥调度算法

岸桥分配发生在船舶泊位和离港期间。考虑下一船舶到达对其的影响，如果下一到达船舶的最优泊位处于当前船舶的左边，则其右边的岸桥被优先分配给当前船舶。否则，左边岸桥。岸桥分配分2 个阶段。

（1）泊位时的岸桥分配算法。泊位阶段，分配给船舶的岸桥主要考虑rpi和bpi+1。以bpi+1＞rpi为例，设置rpi为基线，考虑岸桥状态和非交叉约束，添加处于基线左边的岸桥到headCrane；其他添加到endCrane。根据船舶需求的岸桥数量，优先分配在headCrane 且与船舶最近的岸桥给船舶。如果headCranes的岸桥量不足，则选择就近的岸桥加入工作组，且为船舶i工作的岸桥量不能超过NCi。泊位岸桥分配算法QA_B流程如图4 所示。

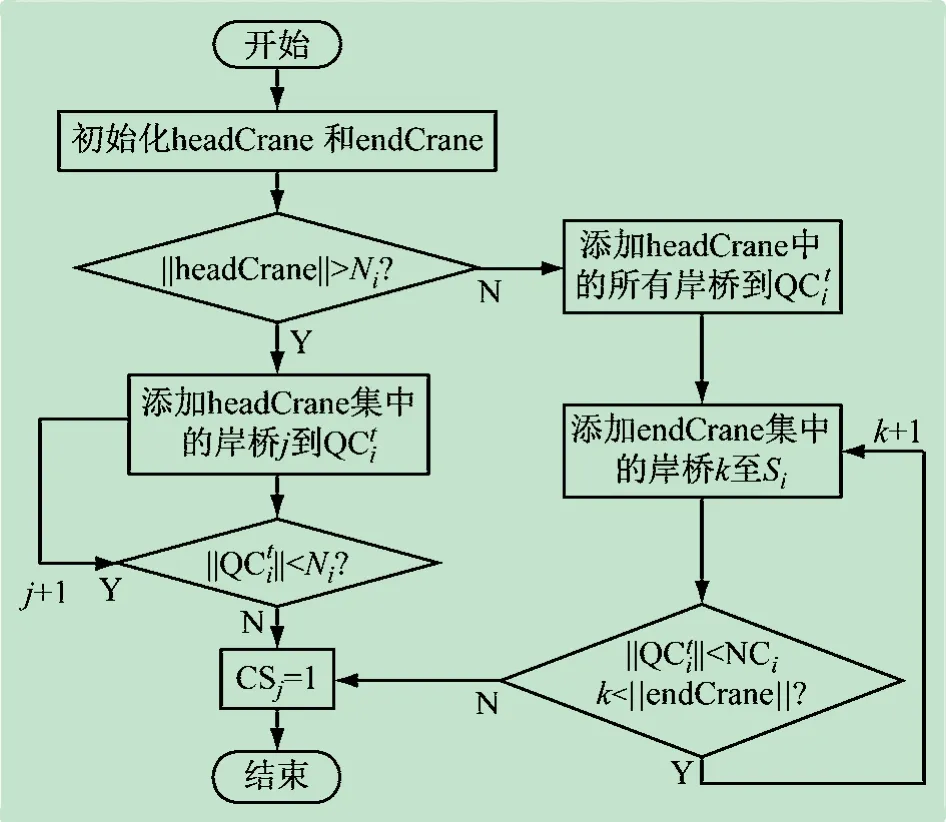
图4 泊位时岸桥分配算法

（2）离港后的岸桥分配算法。待船舶完成任务离开港口后，岸桥此时变成空闲资源。同时，可能有些船舶无法按时离港，所以这些空闲岸桥需要在这些逾期船舶中重新分配。不同于泊位时的分配，船舶离港后的岸桥分配需满足最小化延时处罚代价的需求。离港岸桥分配算法QA_D流程如图5 所示。

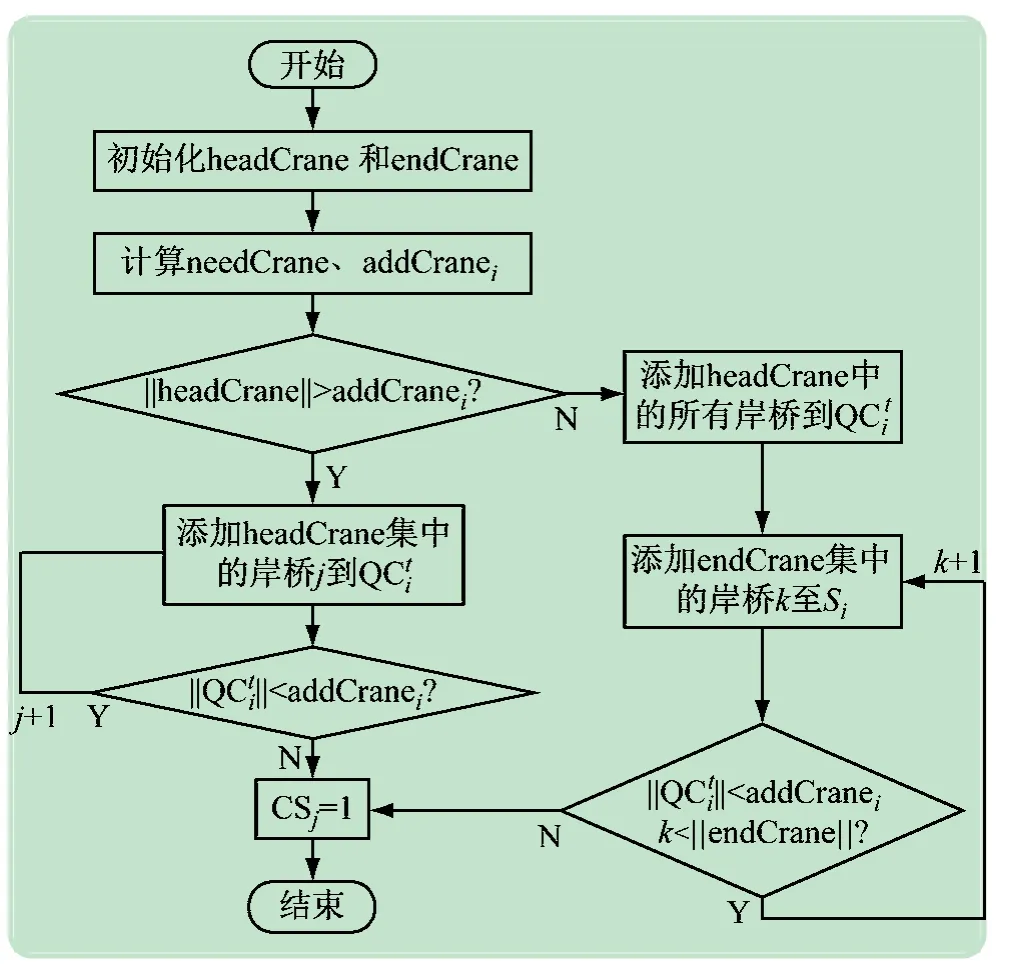
图5 离港时岸桥分配算法

基于BA、QA_B和QA_D3 种算法，本文提出一种多阶段协作式泊位与岸桥调度算法，步骤如下。

步骤1初始化船舶信息，包括：船舶到达时间、要求离港时间、优先泊位、集装箱长度和数量，获取港口泊位序列。

步骤2选取泊位序列中的泊位i。基于BA、QA_B和QA_D算法为船舶i分配泊位。时间窗口移至tai。

步骤3从BW中选取最早离港船舶j。如果tdj＞tai+1（i+1∈sequence），返回步骤2；否则，转步骤4，且j ＝0。

步骤4选取当前离港船舶j，时间窗口移至tdj并释放QCjand LCj。

步骤5检查BW 中是否有船舶超时。如有，添加至OTS，k＝0；否则，转步骤8。

步骤6选取OTS中的船舶k，基于QA_B和QA_D算法分配岸桥，并更新tyk。

步骤7检查OTS中是否所有船舶已经处理或所有空闲岸桥已经分配给船舶。如是，转步骤8，w＝0，否则，k＝k+1，转步骤6。

步骤8选取WB 中的船舶w作为目标船舶，并基于BA算法为其分配泊位。

步骤9检查WB中是否所有船舶已经处理。如不是，w＝w+1，转步骤8，否则，转步骤10。

步骤10如tdj+1＜tai+1，时间窗口移至tdj+1，j＝j+1，转步骤4，否则转步骤11。

步骤11如所有船舶完成作业，停止仿真并输出结果，否则，i＝i+1，转步骤2。

3.3 模型表示与调度框架

为便于求解调度方案，以粒子群算法PSO 对泊位和岸桥分配进行编、解码。粒子群算法是一种受鸟群活动启发的群体智能技术［16］，其核心是通过协作和粒子间的信息共享寻找最优或次优解。本文利用一种二维数组记录粒子位置的基础信息及其次序，见表1。第一维是粒子的位置信息，第二维表示数据的次序。PSO更新粒子的位置信息后，粒子次序同步进行计算更新。

表1 粒子位置的二维数组

根据xi的值，可以得到每个si的值。以纵向序列表示船舶的标识号ID，si的次序可映射为船舶的泊位次序。如表2 所示，数组表示10 个船舶的次序。通过以上的编码方法，表2 中的服务序列可表示成表3。

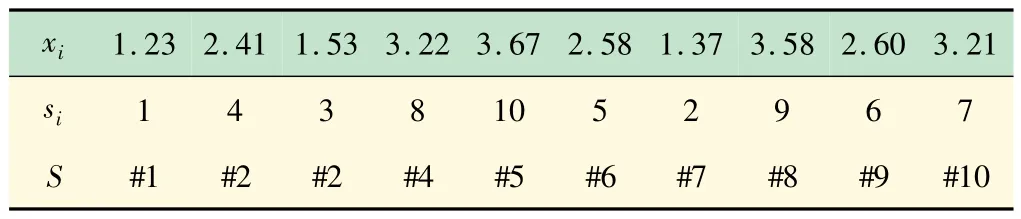
表2 问题编码

表3 服务序列解码

基于以上分配算法和粒子群算法，设计了一种实现岸桥和泊位优化分配调度框架模型，如图6 所示。模型主要包括调度算法、分析和优化等模块，其中，调度算法模块负责实现侯选调度计划和输出统计结果，分析模块负责转换编码信息为可用信息并传送到调度算法模块，同时接收调度算法模块的数据，优化模块负责通过粒子群算法实现主要调度方案的产生，并更新粒子群和选择优化结果。

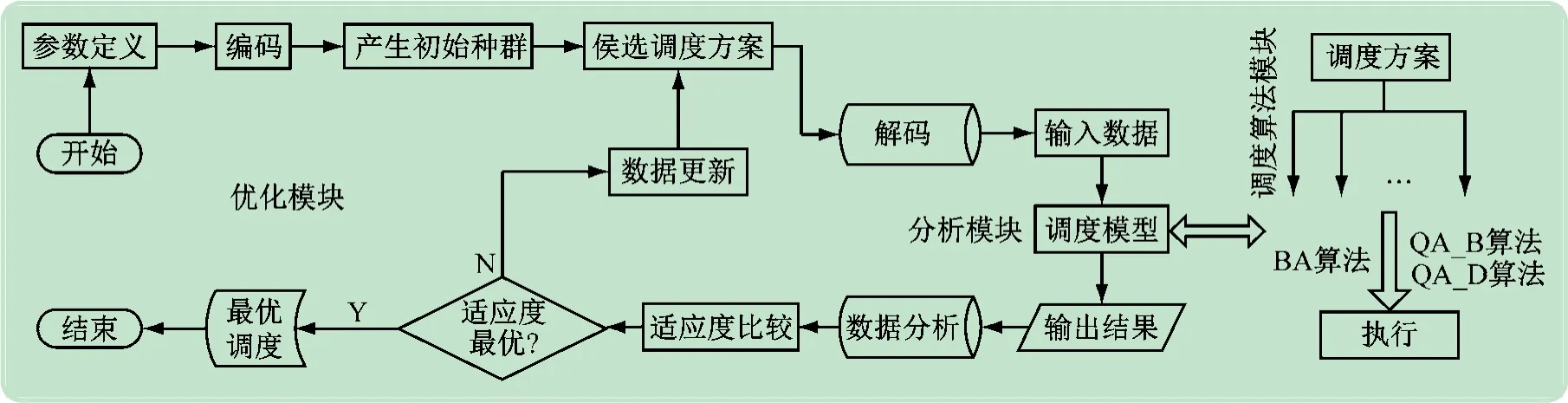
图6 泊位与岸桥多阶段协作调度框架

个体初始化通过粒子群算法形成，并作为候选方案，见表2。解码操作之后，通过调度算法模块将每个个体解析为可用信息。分析模块转换解析数据至调度算法模块以模拟集装箱码头的作业过程。通过这个仿真框架，计算出侯选方案的结果，并将结果传送到优化模块，并从中选择最优解。如运行满足停止条件，就输出最优解。否则，实施更新操作，更新个体信息进行下一次迭代。通过该模型，能实现协作式调度的仿真和最优化。

4 算例分析

基于文献［8］，建立测试案例对算法进行验证，采用Matlab R2009a平台并结合图6 所示的调度框架编写算法仿真程序。设置码头长度为1500 m，在一次调度周期内，假设8 艘集装箱船舶依次抵达港口，船舶的基本数据选取长江上游某大型港口的部分统计数据设计算例，见表4。对于船舶1 ～6 每小时惩罚代价和每米额外处理代价设为5000 ＄／h和400 ＄／m。船舶7～8 设为3000 ＄／h 和200 ＄／m。假设现有12 个岸桥部署在泊位附近，岸桥的生产率为40 TEU／h。泊位船舶间的安全距离设为30 m。测试中，选取先来先服务调度算法（First Come First Serve，FCFS）作为比较算法进行性能比较。

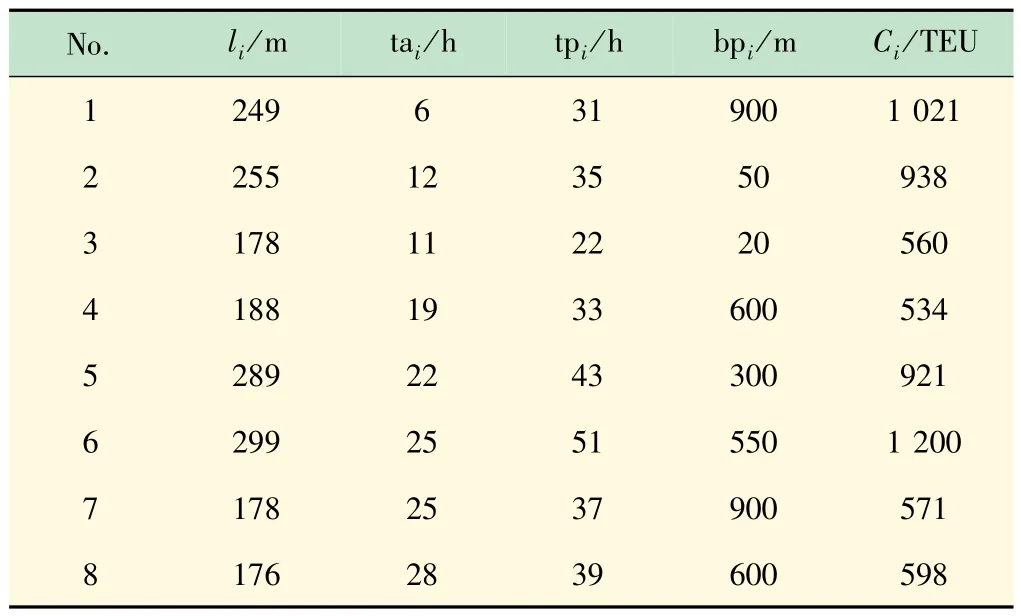
表4 船舶参数设置

FCFS算法中，船舶按时间优先级进行泊位。最早到达的船舶将优先进行泊位，其目标是最短化船舶的总等待时间。调度计划见表5，其中，Tg为要求的离港时间与实际离港时间的差值，Pg为首选泊位与实际泊位的差值。船舶在港的总时间为86 h，总处理时间为86 h。所以船舶无须等待即可泊位。

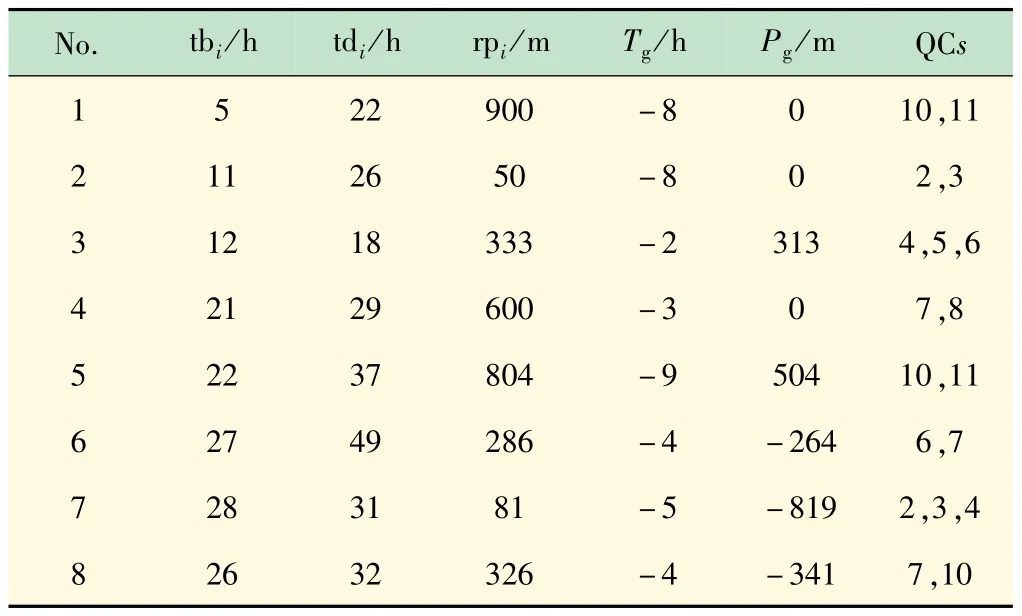
表5 FCFS算法结果

本文算法中，船舶的泊位顺序由粒子群算法决定，其结果见表6。可见，船舶在港时间总和为105 h，工作时间为85 h，等待时间为20 h。

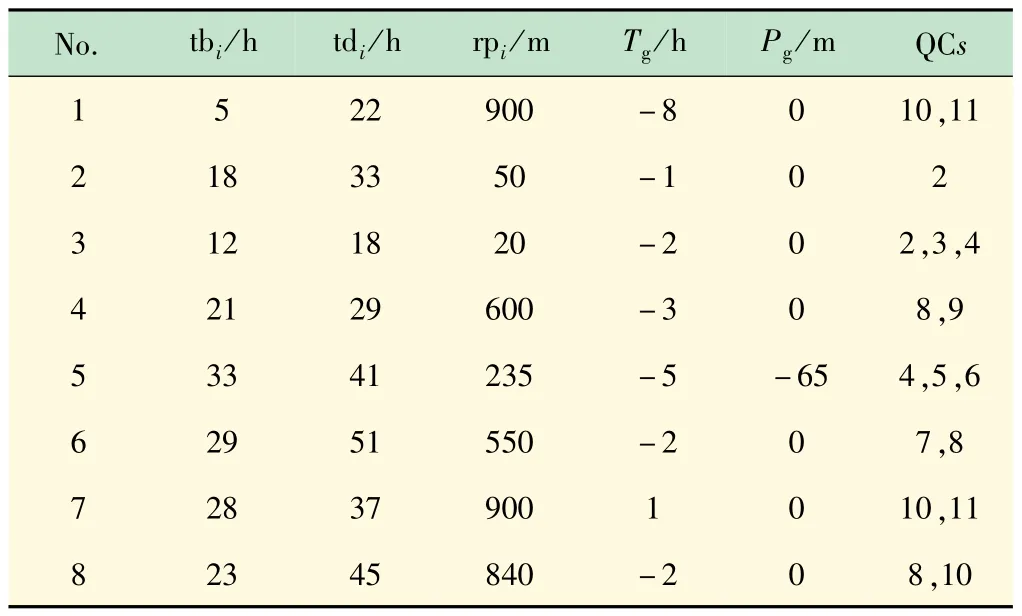
表6 本文算法结果

算法比较见表7，表中，TI 为船舶总在港时间，TP为总处理时间，TW为总等待时间，D为惩罚代价，P为泊位附加代价。显见，FCFS算法可以降低船舶的等待时间，但由于泊位不在最优（首选）位置，附加代价成为泊位代价的主要部分。通过协作调度优化可满足大部分船舶对首选泊位的需求，并通过岸桥分配算法也能确保大部分船舶能按计划完成处理任务。比较第1种算法，本文算法的目标代价显然更加经济。

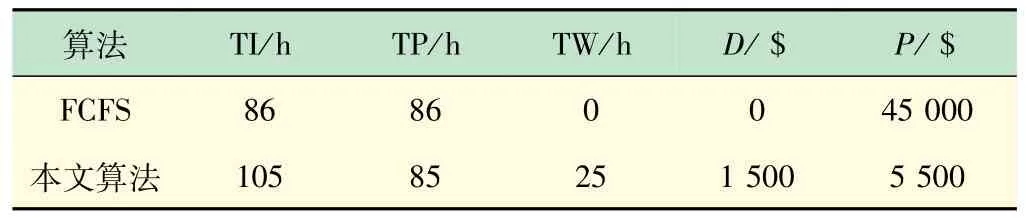
表7 两种算法比较

本文比较了2 种算法获得最终解所需时间和得到相同解时所需时间，该时间也反映了算法本身的收敛性。如图7 所示，当求解问题规模增大时，2 种算法求解最终解所需要的时间是递增的，本文算法略高于FCFS算法，这是由于本文算法在每次迭代求解时均需对泊位分配和岸桥调度进行优化，以降低总代价，计算量大于FCFS算法。可见，若本文算法得到与FCFS相同的解即停止运算，该时间则略低于FCFS 得到相应解的求解时间。综上，本文算法为最小化总体代价，其运行效率在调度规模增大时仍然是可以接受的。

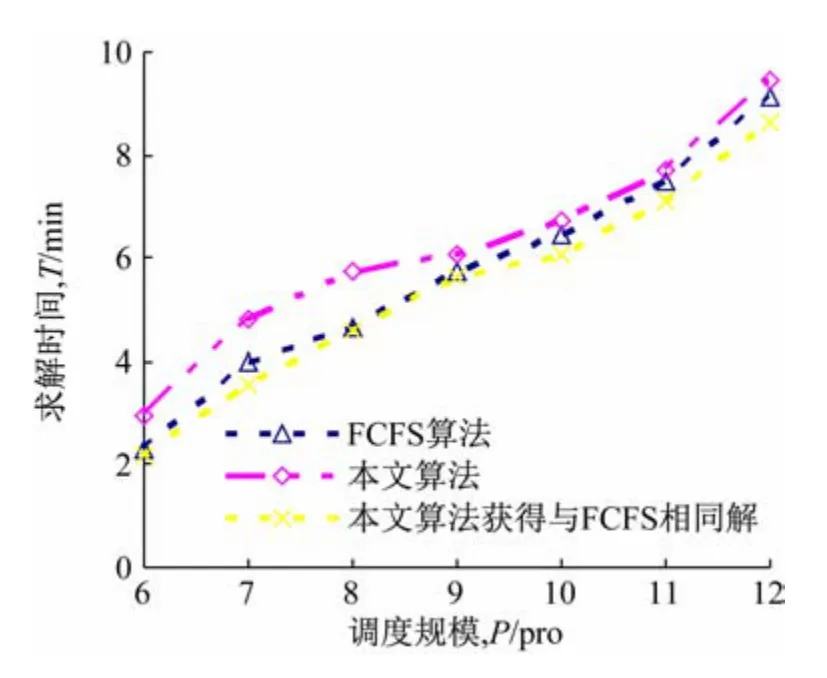
图7 3种算法求解效率

5 结语

为解决集装箱码头连续泊位和岸桥的协作调度分配，提出一种结合启发式算法和粒子群算法的优化模型。通过将码头划分为多个倚靠单元，船舶的倚靠位置和岸桥可以表示成单元序列。在泊位阶段，通过BA算法将单元序列分配给船舶。考虑到码头作业的多阶段性，提出QA_B 和QA_D 算法进行岸桥分配。结果表明，尽管延时代价更高，且最终解的求解时间略长，但本文算法的的总代价低于FCFS 算法，这表明模型对于泊位和岸桥的协作调度分配是可行有效的。