光电法受迫振动实验的研究与应用

张雅男， 艾真珍， 刘 通， 魏子韬， 钱黎明

（南京信息工程大学a.工程训练中心；b.长望学院；c.物理与光电工程学院，南京 210044）

0 引言

振动是自然界及人类生产实践中经常发生的一种普遍运动形式，机械振动则是指物体在某一确定位置附近做来回往复的运动。振动系统在弱阻尼力和一个连续的周期性外力作用下进行的振动，即受迫振动［1］。在日常生活中，如热矿筛之类的筛分设备，振动输送机类的输送设备等，都是利用了受迫振动的特点。但同时，受迫振动也有很多危害，比如桥梁、车轨、高大建筑等的受迫振动，会影响建筑的安全性，甚至危害人体生命安全［2-3］。所以，对物体的受迫振动观测与研究非常必要。

近代物理实验中利用玻尔共振仪进行受迫振动规律的研究。通过电机周期性对摆轮施加推力，能够测量得到摆轮受迫振动的幅频特性和相频特性［4］。虽然玻尔共振仪能够看到金属圆盘的受迫振动，但在日常生活中，大多数受迫振动是由肉眼无法辨别的。只有当受迫振动的振幅达到最大，即共振，才能容易观察到。与玻尔共振相比，本实验以更常见的玻璃杯为对象，通过声波使其受迫振动。利用光杠杆将玻璃杯的微小振动放大，用图像分析测量其振幅、用光电转换测量振动频率。在观察玻璃杯的受迫振动、共振现象的同时，还可以测量得到玻璃杯受迫振动的幅频特性曲线。

1 受迫振动

1.1 受迫振动的理论模型

1983 年，学者French［5］利用微元法推导出空玻璃杯以及玻璃杯充入一定液体后，固有频率的理论计算方法。将玻璃杯简化为空圆柱模型［6］，当空杯子在周期性外力作用下进行受迫振动时，空玻璃杯的杯壁微元振动方程可写为［7］

式中：η为圆柱形玻璃杯形变；η0玻璃杯的最大形变；ω为周期性外力的圆频率；t为时间。玻璃杯的总能量

式中：K为动能；U为弹性势能；A、B为常数。由式（1）、（2）可得空玻璃杯固有频率

若将玻璃杯壁上任意一点振动看作是沿z轴的一维简谐振动，可将式（1）改写为

式中：f（z）为微元在振动方向上的函数；φ为某微元的方位角。根据简谐振动能量，可得动能和弹性势能分别为：

式中：R为圆柱形玻璃杯内径；H为高度；a为玻璃杯厚度；ρg为玻璃杯密度；E为弹性模量。该玻璃杯理论模型可等价为无数根下端固定，上端自由的均匀弦构成。根据Rayleigh 的声学理论［8］，式（5）中的振动函数具有如下形式：

式中，C、D、β 都是常数。此时，有空玻璃杯的固有频率为

若将某种液体加入玻璃杯时，可得到空杯子和加入液体后系统的ν0之间的关系为

式中：ρl为杯内液体密度；νd为加入液体高度为d时系统的ν0；α为耦合系数，是常数。

1.2 实验装置设计

本实验设计并搭建的装置包括声波产生系统、玻璃杯及受迫振动测量系统，整体装置如图1 所示。实验时，将信号源与功率放大器连接后再接入扬声器，功率放大器使扬声器发出的声波达到一定强度，从而玻璃杯能够产生受迫振动。

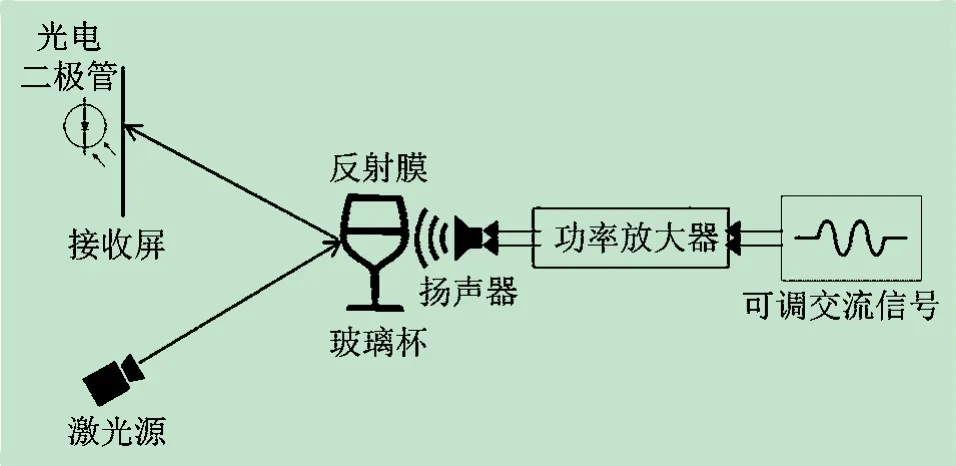
图1 受迫振动实验装置示意图

1.3 受迫振动的测量

1.3.1 受迫振动振幅的测量

即使通过功率放大器增大声波的强度，但玻璃杯受迫振动也是肉眼不易观察的。对其振动振幅的测量必须寻找合适的方法才能够测量准确。本实验采用大学物理实验中“静态拉伸法测量金属丝弹性模量”［9］相同的方法，利用光杠杆将玻璃杯微小振动放大至可测量。图1 中，将一束激光照射到玻璃杯上。通过玻璃杯上粘贴的薄反射膜，使激光反射到接收屏上。当玻璃杯作受迫振动时，经过反射膜反射的光斑，在接收屏上的位置也在作相应的振动，这个振动是容易被观察并测量的。

图2 所示为不同声波状态下光斑宽度随强迫力（声波）频率增大而变宽的过程。图2（a）为没有开启声波，玻璃杯静止时，接收屏上看到的是一条细光斑；当开启声波，玻璃杯受迫振动稳定后，玻璃杯的小微元、玻璃杯上的反射膜、通过反射膜反射到光屏上的光斑位置，均在作振动，虽然因人眼分辨能力无法观察到的光斑的振动，但直观上可以看到光斑变宽［见图2（b）］；声波频率为547 Hz 时，光斑宽度达到最大值［见图2（c）］。根据受迫振动原理，对于某振动系统，在阻尼一定的条件下，受迫振动的振幅随驱动力圆频率的增加而增加，达到最大后，又随驱动力圆频率的增加而减小［10］。

图2 不同声波状态下光斑宽度变化比较

仅用肉眼观察到光斑宽度变化并不能进行量化的测量，也无法研究声波频率对玻璃杯受迫振动的影响。本文利用光杠杆原理，将玻璃杯受迫振动时振幅的变化放大为光斑宽度的变化。根据前述玻璃杯受迫振动的理论模型，玻璃杯微元受迫振动时满足简谐振动方程，图3 所示为光斑宽度与玻璃杯微元振幅关系示意图。由图3 可得如下关系：

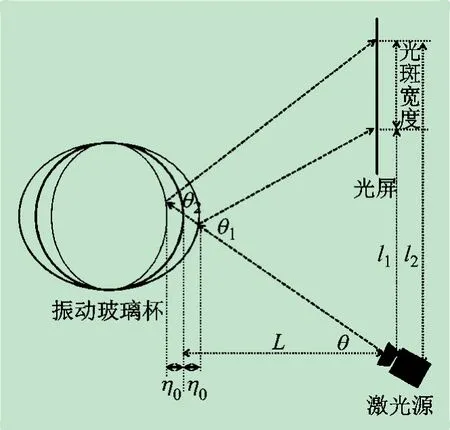
图3 光斑宽度与玻璃杯微元振幅关系示意图

得出光斑宽度

玻璃杯微元受迫振动时，在其振动方向产生的最大位移为η0，因振幅较小，故θ≈θ1≈θ2，则

当激光源、玻璃杯及光屏位置固定时，光斑的宽度正比于玻璃杯微元受迫振动的振幅。根据本实验设计装置，可以将玻璃杯在不同声波激励下受迫振动的振幅测量转换为光斑宽度的测量。

1.3.2 光斑宽度的测量

已有文献中采用米尺测量光斑宽度，但误差较大［5］。为更精确的测量光斑在不同频率声波激励下的宽度，本实验利用Python 软件进行图像分析，求解光斑宽度。

如图4 所示为通过图像处理得到光斑宽度的过程：①在某频率声波激励下，光斑位置作振动，用相机拍摄此时光斑［见图4（a）］；②将其去色得到灰度图［见图4（b）］；③调整并设置合适的阈值，把灰度图像变成只有黑白两种像素点的二值图像［见图4（c）］；④通过形态学操作［11］填充光斑内部的黑色噪点，得到可以计算光斑宽度的最终的图像［见图4（d）］。扫描图4（d）的若干行，第1 个白色像素点与最后1 个白色像素点之间的差值，计算平均值，得到光斑的宽度。用Python软件进行图像分析，所得光斑宽度只是1 个相对值，并不是光斑的真实宽度。实验时，固定所有仪器的位置，只改变声波的频率，可得到不同声波频率下，光斑的相对宽度。利用图像分析软件可以精确计算出不同声波频率下光斑的宽度，从而更准确地反映不同声波频率下玻璃杯受迫振动的振幅。

1.3.3 光斑位置振动频率的测量

本实验利用光电转换模块测量光斑位置振动的频率，用以反映玻璃杯稳定受迫振动的频率。图5（a）为带有pin二极管的iv转换放大电路实体装置，图5（b）是其电路图。激光经贴在玻璃杯上的反射膜反射，被装置中的pin二极管接收转换为电流信号；再将电流信号利用运算放大电路，变为放大的电压信号后［12-13］，输入示波器进行观测。测量时，使二极管位于光斑宽度的最边缘，光斑位置周期变化，示波器上将显示其对应电压信号的变化，如图6 所示。同时测量出信号的周期，由此得到该信号对应光斑的振动频率为475 Hz。

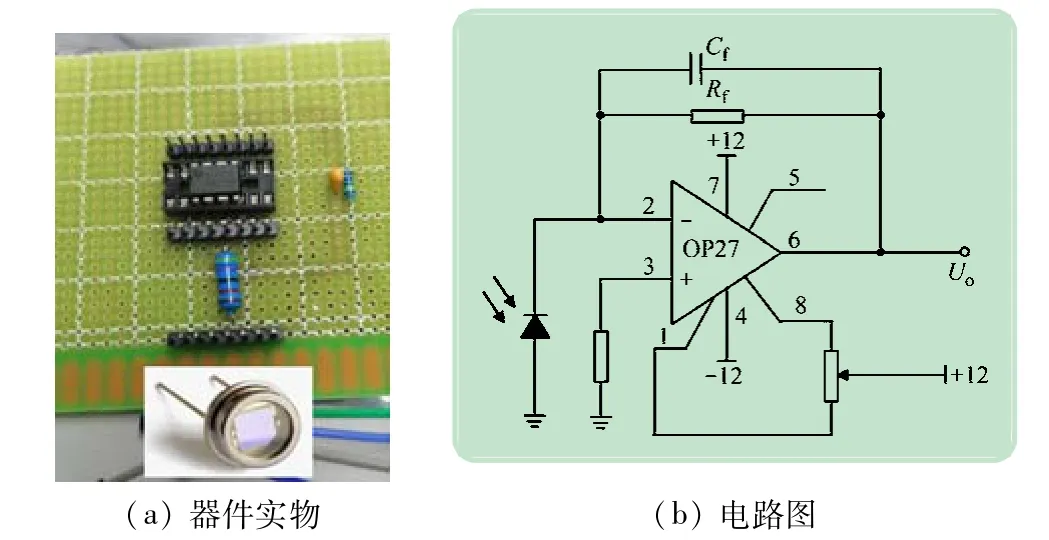
图5 iv转换放大电路实体装置及其电路图

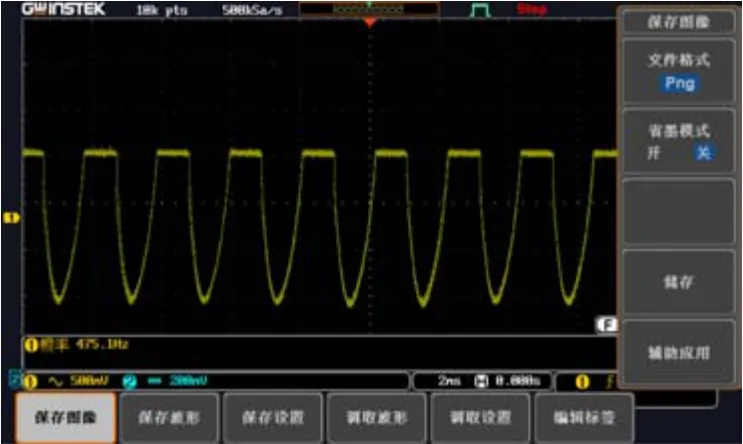
图6 玻璃杯上反射由示波器测量的电压信号截屏

2 测量结果及数据分析

利用本文设计的装置中的声波产生系统，发出声波使玻璃杯受迫振动，当玻璃杯受迫振动稳定后，在声波频率分别为1120、1122、1124、1126、1128、1130 Hz时，对应测得光斑位置振动频率分别为1120.0、1122.1、1124.0、1126.0、1127.8、1130.1 Hz，由此可知光斑位置振动频率与声波频率基本相符。

如图7 所示为玻璃杯受迫振动的幅频特性曲线。由图7（a）可知，随着声波频率逐渐变大，光斑的宽度也随之变宽，意味着玻璃杯受迫振动的振幅也随声波的频率而变大。根据受迫振动理论，当受迫振动振幅达到最大值时，系统发生共振，此时的声波频率最接近玻璃杯的ν0，称之为共振频率［1］。图7（a）中所示的一玻璃杯受迫振动过程中的最大光斑宽度，其对应的频率，即为该玻璃杯的ν0。通过音叉棒敲击玻璃杯振动发声，测量该声波的频率，也可以得到玻璃杯的ν0［7］。

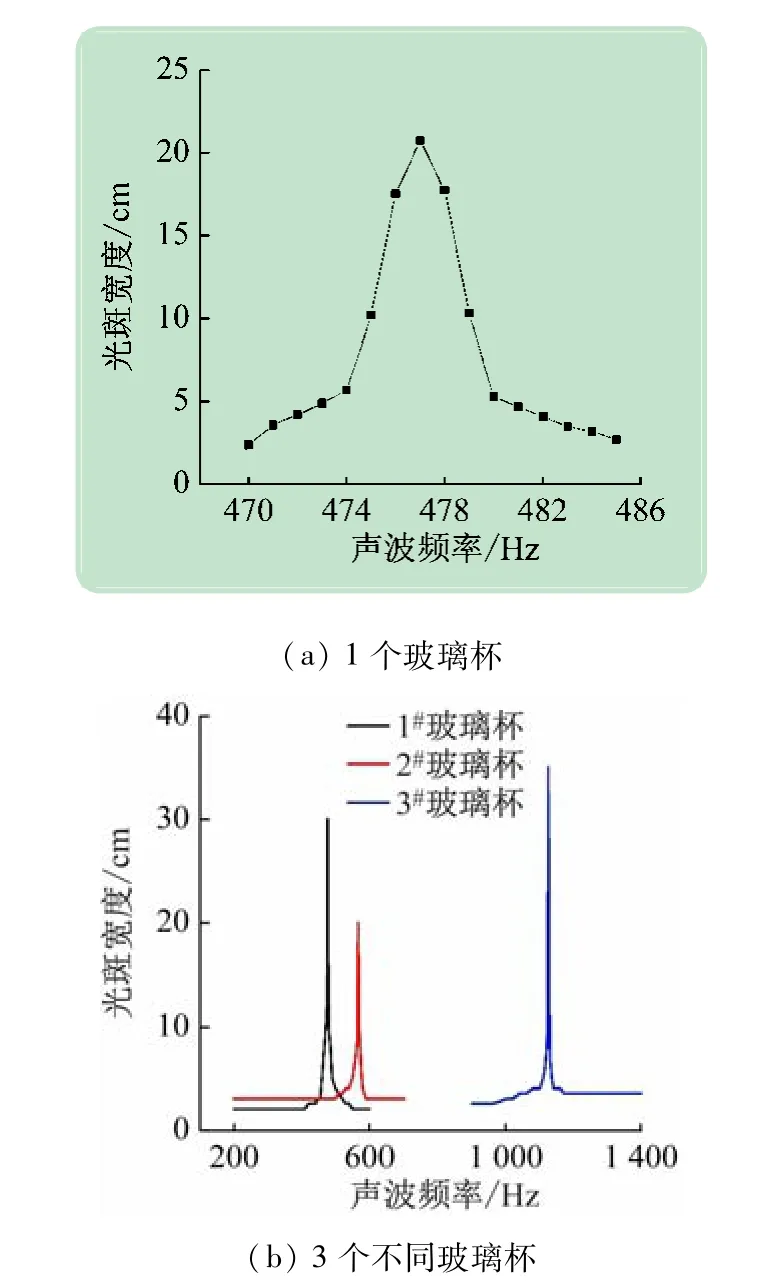
图7 玻璃杯受迫振动幅频特性曲线

表1 为依据玻璃杯的物理尺寸及式（8）计算得到的ν0，其中α ＝1.25［14］，E＝70 GPa［6］，ρ ＝2.50 g／cm3（用固体密度测量仪测得）。

表1 玻璃杯ν0 理论计算结果

表2 所示为用2 种方法测量3 个不同玻璃杯的ν0与理论计算结果比较，由表可知，用本实验装置测量空玻璃杯的ν0，准确性非常高。图7（b）所示表2 中3 个不同高度、厚度、容量的玻璃杯受迫振动幅频特性测量结果，均符合受迫振动规律。与大学物理实验中《波尔共振》实验相比，本实验装置虽然无法测量出受迫振动系统的阻尼系数以及相频特性，但可以用简单的仪器及其他课程的相关方法，测量出不同玻璃杯的受迫振动幅频特性曲线及玻璃杯的ν0。

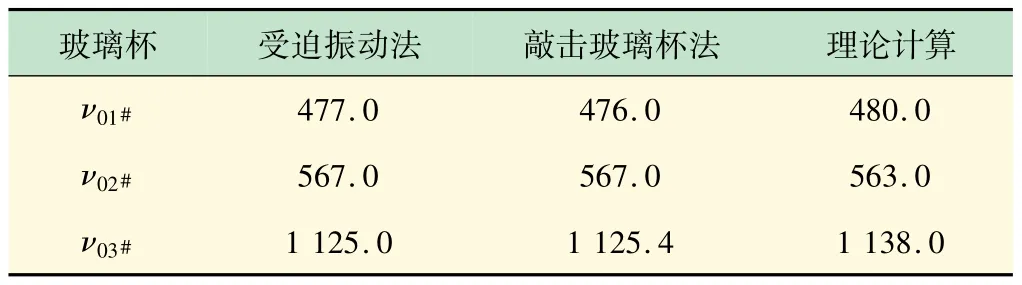
表2 2 种方法测量玻璃杯的ν0Hz

3 受迫振动的拓展及应用

3.1 加入液体改变玻璃杯系统的ν0

玻璃杯的ν0受到很多因素的影响，如玻璃杯中加入不同体积的同种溶液后，玻璃杯与液体组成的系统，其ν0会随之发生变化。用本实验装置，进一步研究并分析因加入液体体积变化而导致玻璃杯系统ν0变化的趋势。

（1）加入纯净水的玻璃杯ν0变化。图8 所示为不同尺寸玻璃杯的共振频率与加水体积量变化的实测曲线及对应运用式（8）计算所得的理论曲线。由图可知，测量的3 个不同的玻璃杯，其共振频率均随着加入水的体积增大而降低。本实验得到的玻璃杯充入纯净水后共振频率随体积变化趋势，与理论计算基本相符。

图8 不同玻璃杯中加入不同体积水的共振频率曲线比较

（2）加入不同密度液体的同一玻璃杯ν0变化。表3 为加入不同密度的溶液后，同一玻璃杯共振频率的理论计算值与实测值的比较，由表可知，在1＃玻璃杯中充入300 mL不同密度液体后，用共振法测量的共振频率与理论计算的结果基本相符，进一步证实本实验方法的可靠性。

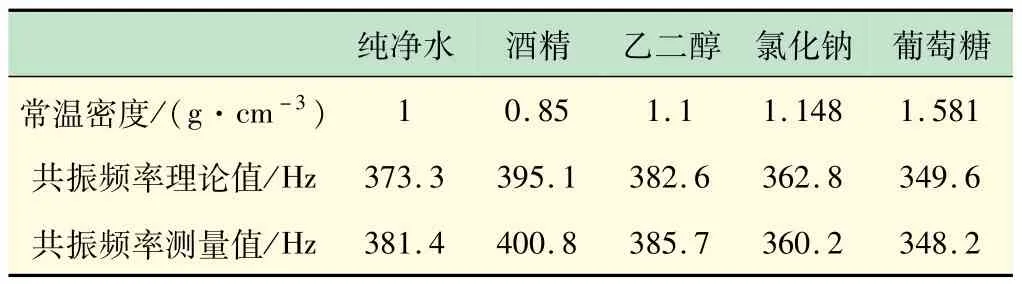
表3 1＃玻璃杯加入不同密度溶液共振频率计算值与测量值比较

3.2 测量溶液浓度

表3 中所列除水外的4 种溶液都是某种物质溶于水形成的，理论计算时，涉及该溶液的密度，而不同密度又对应于不同的溶液浓度。据此推断，同种溶液不同浓度也会对玻璃杯的共振频率产生影响，若能找到浓度与共振频率之间的关系，也可以利用本实验装置，测量透明液体的质量浓度。

以1＃玻璃杯为容器，测量3 种溶液在不同质量浓度时的共振频率，同时依据式（8）计算玻璃杯中充入一定体积不同密度溶液时的共振频率。图9 所示为1＃玻璃杯中加入3 种不同溶液浓度与共振频率的实测曲线及运用式（8）计算所得的理论计算曲线对比，由图可见，理论计算的共振频率与共振法测量的频率有一定的差别，但3 种溶液共振频率随浓度变化的趋势与理论基本相符，因此，利用共振法可以测量溶液浓度。如图10 所示为用本实验装置实测不同乙二醇溶液浓度与共振频率的拟合曲线图，并取得拟合曲线方程，从而可配置任意浓度的乙二醇溶液，测量其共振频率，代入拟合公式，计算出其浓度。从理论及几种溶液测试结果都能够说明，在本实验装置上利用共振法，可以测量溶液浓度。

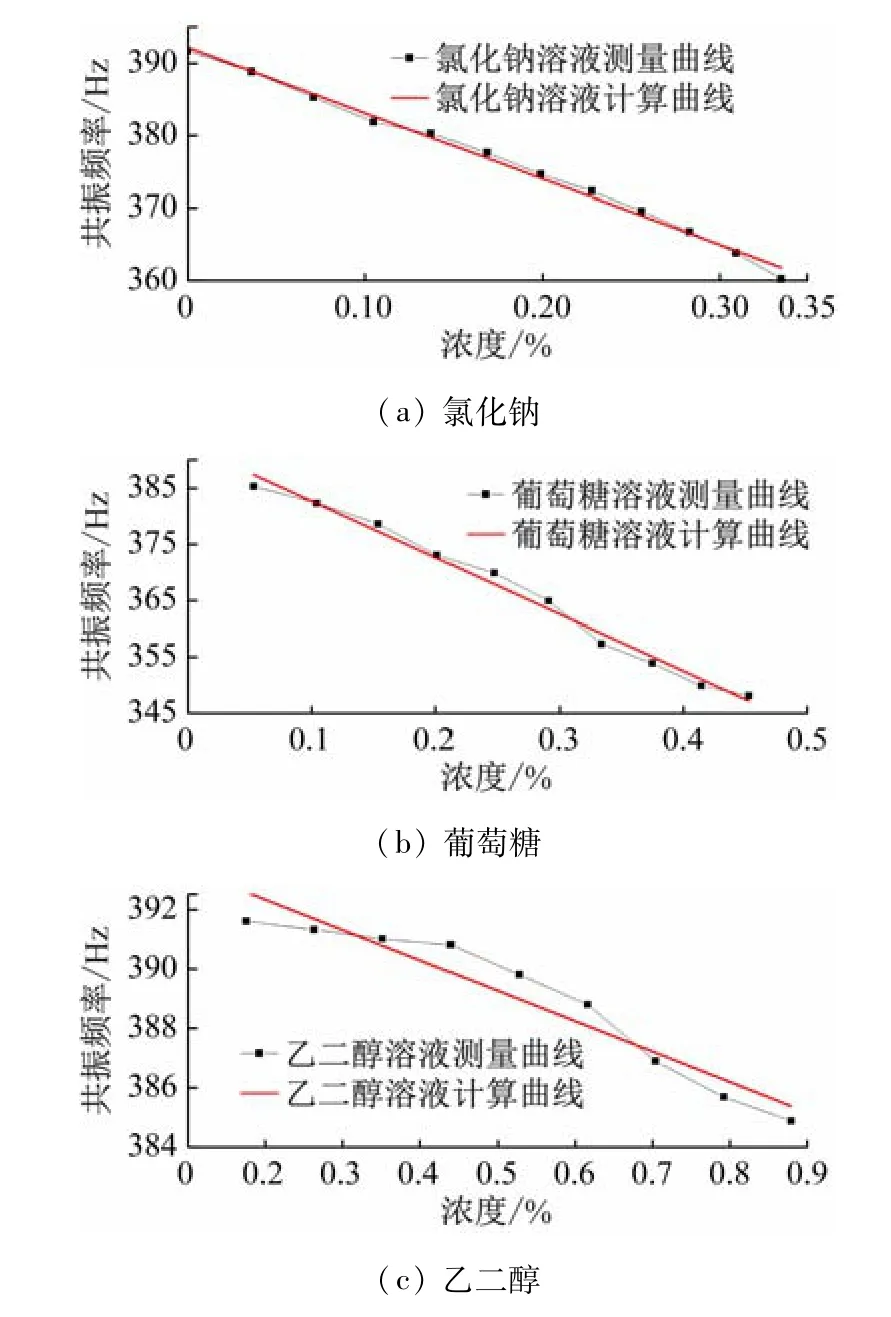
图9 3种溶液的质量浓度与共振频率曲线比较

图10 不同浓度的乙二醇共振频率拟合曲线

图9 中的3 种溶液，其理论计算得到的浓度与共振频率关系均为线性，但从图10 的实测数据可见，乙二醇的浓度与共振频率的关系为非线性拟合曲线。配置的待测溶液浓度为50%，测量其共振频率为390 Hz。将其代入图10 的拟合方程，计算得到溶液浓度为52%，相对误差4%，在可接受范围内。虽然拟合曲线与理论曲线差别较大，但根据拟合曲线而求出的溶液浓度误差较小。

4 结语

本文设计并搭建的实验装置，分别进行了玻璃杯受迫振动、水及不同的溶液浓度与共振频率变化的实验测试，结果表明：利用声音使玻璃杯发生受迫振动，实验测量得到3 个不同玻璃杯受迫振动的幅频特性曲线，曲线的峰值对应玻璃杯的共振频率分别为477、567、1125 Hz，与受迫振动理论模型计算3 个玻璃杯的ν0为480、563、1138 Hz基本相符；在玻璃杯中加入不同体积、不同密度的液体后，玻璃杯的共振频率均会发生变化，变化趋势与理论计算趋势相符；将相同体积不同浓度的乙二醇溶液加入玻璃杯中，测量其共振频率，浓度与共振频率拟合得到方程，测量任意浓度乙二醇溶液的共振频率，代入拟合方程得到的溶液浓度误差较小，证明可以利用本实验装置及方法测量溶液的浓度。非线性拟合结果也说明理论计算模型仍然可以根据具体实验情况进行改进，考虑更多的因素才能使得理论计算更加准确。利用本实验装置测量液体浓度并没有考虑温度的影响，若进行变温测量，得到的拟合方程有可能会更加准确［15］。

·名人名言

知识是一座宝库，而实践则是开启宝库的钥匙。

———托马斯·富勒