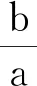以课堂教学评价视角谈“椭圆离心率”概念的引入*
顾晓峰 (江苏省锡山高级中学 214074)
1 问题提出
离心率是刻画椭圆形状的重要量,在引入此概念前,学生头脑中对不同的椭圆形状已有直观认识,但定性的感知要上升为定量的描述,这既是他们直观想象水平与数学抽象素养的生长点[1],也是“椭圆的简单几何性质”中的教学难点.那么,离心率到底应该如何引入?对于大量的相关教学设计该如何借鉴?为了回答这一问题,笔者从课堂教学评价视角出发,基于实际课堂案例,从教师教学行为和学生学习行为两个维度对教学过程进行评价.一方面,利用观察量表对相应指标进行赋分,量化教学结果;另一方面,充分关注教师能动性、学生态度变化等质性因素,既“有章可循”,又不“受制于形”.最后,基于评价分析,笔者形成自己的教学设计并进一步实践与反思.
2 “椭圆的离心率”教学中存在的问题
笔者以本主题的学校常态课、公开课、视频课(评优课、示范课)以及期刊论文中相关教学实录(设计)为素材,收集了18节课例.利用文[2]提供的数学深度教学课堂评价表(表1)进行课堂观察与过程性评价.需要指出的是,以下讨论不再呈现具体赋分,而是基于赋分结果与课后访谈,聚焦于“椭圆离心率如何引入”的教学处理中存在的主要(共性)问题.

表1 数学深度教学课堂评价表
人教A版教材中关于椭圆离心率的引入如图1所示.

图1
2.1 直接引进a,c进行刻画,忽视概念的探究性

2.2 不能立足于学生视角,忽视定义的合理性

2.3 过分强调离心率的背景意义,忽视认知的阶段性
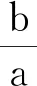
基于以上评价分析,离心率概念的引入教学应起于学生的最近发展区,从直观到微观,从具体到抽象,通过有效的问题串启发学生的认知,逐步探寻量化椭圆扁圆程度的可能性与合适性.同时,教学需考虑到信息技术使用的必要性,突出师生间的多元互动,使学生较为深刻地理解离心率这一概念本质.笔者结合分析并重构教学,以下展示具体过程.
3 教学重构的实录
师:我们只需输入方程就可以生成图象了,大家要不随便说个方程来试试!
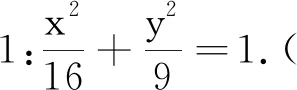
师:现在有两个椭圆图象,从形状上看,它们有没有什么差异?
生(众):一个扁些,一个圆些,红色椭圆更圆.
设计意图通过GGB作图激发学生直观想象,自然地发现椭圆间扁圆程度的区别,培养学生发现问题的探究意识.
师:那你们能不能说一个比红色椭圆还要圆的椭圆?
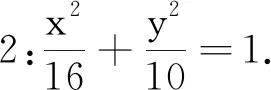
师:果然更圆了!生2你是怎么想到这个方程的?
生2:因为要让椭圆变圆,(在长轴不变的情况下)就要让短轴长变大,也就是b要变大.
师:大家都点头同意生2!那是不是只能通过变化b来改变扁圆程度?
生(众):不是!
师:那你(生3)还有什么别的办法?
生3:也可以让a变小,这样长轴越短,椭圆就显得越圆!
师:很好!那是不是a与b只能变化一个?
生(众):两个可以同时变.
师:那a与b同时变,椭圆的扁圆程度就一定会发生变化吗?
生4:不一定!a与b等比例同时变化时椭圆形状应该不变!
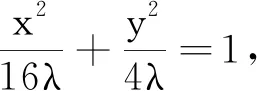
生5:λ在变,椭圆的a2,b2在(等比例)变化,不过椭圆形状没有改变,只是放大或缩小了!
师:很好,那根据实验,如果我们用一个量来刻画椭圆的圆扁程度,你们会想到什么?
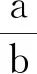
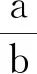
生(众):也可以!
设计意图立足学生视角,通过递进式的问答让学生从直观性上逐步分析引起椭圆形状变化的基本量,培养学生利用控制变量法研究问题的思维策略.在探究活动中,学生能够主动学习,获得经验,充分体会概念建立过程中对合理性的追求,提升他们分析问题的能力.
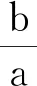
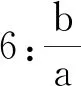
师:为什么它在变大时会趋于1?
生(众):因为b 师:很好!还记得在椭圆的第一节课里,我们已经知道只要给一根绳子,就可以画出椭圆.请大家就利用桌上不同长度的绳子,类比刚刚的研究思路,小组合作探究,能否发现椭圆的扁圆程度还与什么量有关? 设计意图学生经历由直观想象到数学抽象的第一阶段,初步获得了研究问题的方法,于是在第二阶段放手让学生实践,进一步培养学生解决问题的能力.通过第二阶段的探究活动,学生能从不同角度审视数学概念,加深对概念内涵的理解. 生3:我们发现一根绳子的两端如果越靠近,画出来的椭圆越圆,如果越远离,椭圆越扁.说明a一定的情况下,改变c也可以改变扁圆程度. 师:很好,也就是两个焦点越靠近中心(c越小),椭圆越圆;两个焦点越远离中心(c越大),椭圆越扁. 生6:我们发现在绳子两端距离确定的情况下,绳子越长,椭圆越圆;绳子越短,椭圆越扁.也就是c确定时,a越大、椭圆越圆,a越小、椭圆越扁.(教师用GGB进行演示验证) 师:两组同学都用了控制变量法,那有研究同时变化的吗? 生7:我们与前两组同学得到了一样的结果,而且猜想a与c等比例同时变化时,椭圆的形状不变.但用绳子做不出效果,应该可以用GGB做出来!不过我们小组进行了代数推理. 师:怎么推理的? 生7:因为b2=a2-c2,所以a,c按相同比例变化时,b也按该比例变化,按照刚刚的探究,此时椭圆的扁圆程度是不变的. 师:大家的表情说明都很认可生7的分析!这意味着我们还可以用什么量来刻画呀? 师:那就有了类似的问题,它怎么变可以使椭圆更圆,怎么变可以使椭圆更扁呢? 设计意图一方面,教学中需尊重学生的思维习惯,不拘泥知识的呈现顺序,让学生自主分析、归纳和总结实验结果;另一方面,教师需合理掌控课堂进程,使学生观点能汇合到概念主旨,形成认知刺激甚至冲突,进一步认识到椭圆扁圆程度的刻画既不唯一又相互统一. 生(众):偏离中心的程度. 师:那你们觉得用什么量刻画更好? 最后,关于概念课的教学设计笔者还有一点思考:在课堂教学评价中,信息技术是否使用越多越好?课堂是不是越活跃越好?笔者认为,如果技术的使用不能有助于学生把握概念的本质,课堂表面的热闹也没有真正唤起学生的认知冲突,那么这样的设计是理应改进的.如笔者在离心率概念引入的设计上原本是想全面基于信息技术平台,突出过程可视化,激发学生兴趣,但这在一定程度上弱化了学生理性思维的生成,于是在设计上作出调整,着力让信息技术的使用在关键处彰显价值.在实际教学中,笔者既引导学生思考,也放手让学生探究,整个过程学生的反应先缓后快,先冷后热再归于平静,课堂虽没有持续的热闹但却能明显感受到学生思维的碰撞.这些“恰如其分”也是有助于构建良好课堂生态的.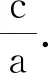




4 教学反思