概率量化岩土各向异性对边坡稳定性的影响

齐磊 丁亚楠

摘 要：由于受到复杂地质过程及荷载历史的影响，具有各向异性的岩土体边坡在自然界中广泛存在。基于表征岩土体参数的随机场模拟数学理论，采用随机有限元、蒙特卡洛模拟和强度折减法，开展了岩土各向异性边坡的稳定性研究。结果表明：与均匀土体边坡相比，岩土各向异性边坡的安全系数相对较低，岩土各向异性对边坡的破坏模式及稳定性有一定影响。岩土各向异性分布范围越大，相邻区域土体之间的相关性越强，发生滑坡的可能性越大。当各向异性倾向角平行于边坡坡角时，安全系数范围的波动性达到最大值。研究成果可为天然边坡的加固方案设计提供参考。

关键词：边坡稳定性；岩土各向异性；随机场；安全系数

中图分类号：TU452                                             文献标志码：A

0 引 言

我国目前正处于经济建设高速发展的时期，地质环境恶劣的西南山区及丘陵地带也开展了大量基础设施建设，这些基础设施直接或间接地受到大型滑坡的威胁[1]。由于大型高陡边坡所处地质条件和构造环境的不同，其失稳的原因部分来源于岩土体参数的空间变异性[2]。在天然边坡可靠度分析和风险评估过程中，国内外学者广泛考虑了土体参数空间变异性的影响[2]。Xiao等[3]指出土体参数空间变异性是影响若干岩土确定性分析问题中最重要的不确定性。

岩土各向异性是天然岩土体风化和沉积过程中分层所导致的一种复杂地质现象，是岩土体空间变异性的一种形式（见图1）。岩土各向异性可在空间任意方向分布，根据其是否有倾角可划分为平行各向异性相关结构（平行分层）和旋转各向异性相关结构（交叉分层）[4]。复杂地质工程或人为过程引起的岩土各向异性不一定是水平的，通常有倾角（以下称为各向异性角）。岩土各向异性对天然岩土体的力学性质和工程特性有一定影响，可能导致复杂地质地貌区域的边坡失稳。Zhu等[5]认为岩土各向异性的力学特性对边坡的稳定性和变形破坏机理的影响不容忽视，而含岩土各向异性的边坡失稳是滑坡灾害最常见的原因。但是，岩土各向异性与边坡失稳破坏机制及稳定性特征的关系至今仍不十分清楚，需要开展岩土各向异性与边坡失稳破坏模式的关系研究。

目前，国内外学者[6-7]对岩土各向异性对边坡破坏模式和稳定性的影响开展了一系列研究。Huang等[8]基于极限平衡法，探讨了土体各向异性对边坡破坏模式和失稳风险的影响，但忽略了各向异性角度对边坡安全系数的影响。Chen等[9]采用极限分析的上限法，深入研究了土体粘聚力的各向异性对边坡失效概率的影响，但该方法需假定边坡的临界滑动面，忽略了临界滑动面的空间变异性。Griffiths等[10]的研究表明有限元方法可以自动识别土体抗剪强度不足以抵抗剪切应力的临界滑动面。基于随机场理论和蒙特卡洛模拟，本文探讨了岩土各向异性（各向异性角及各向异性分布范围）对边坡稳定性及破坏模式的影响，研究成果可为天然边坡加固措施的制定提供一定的技术支撑。

1 岩土各向异性表征方法

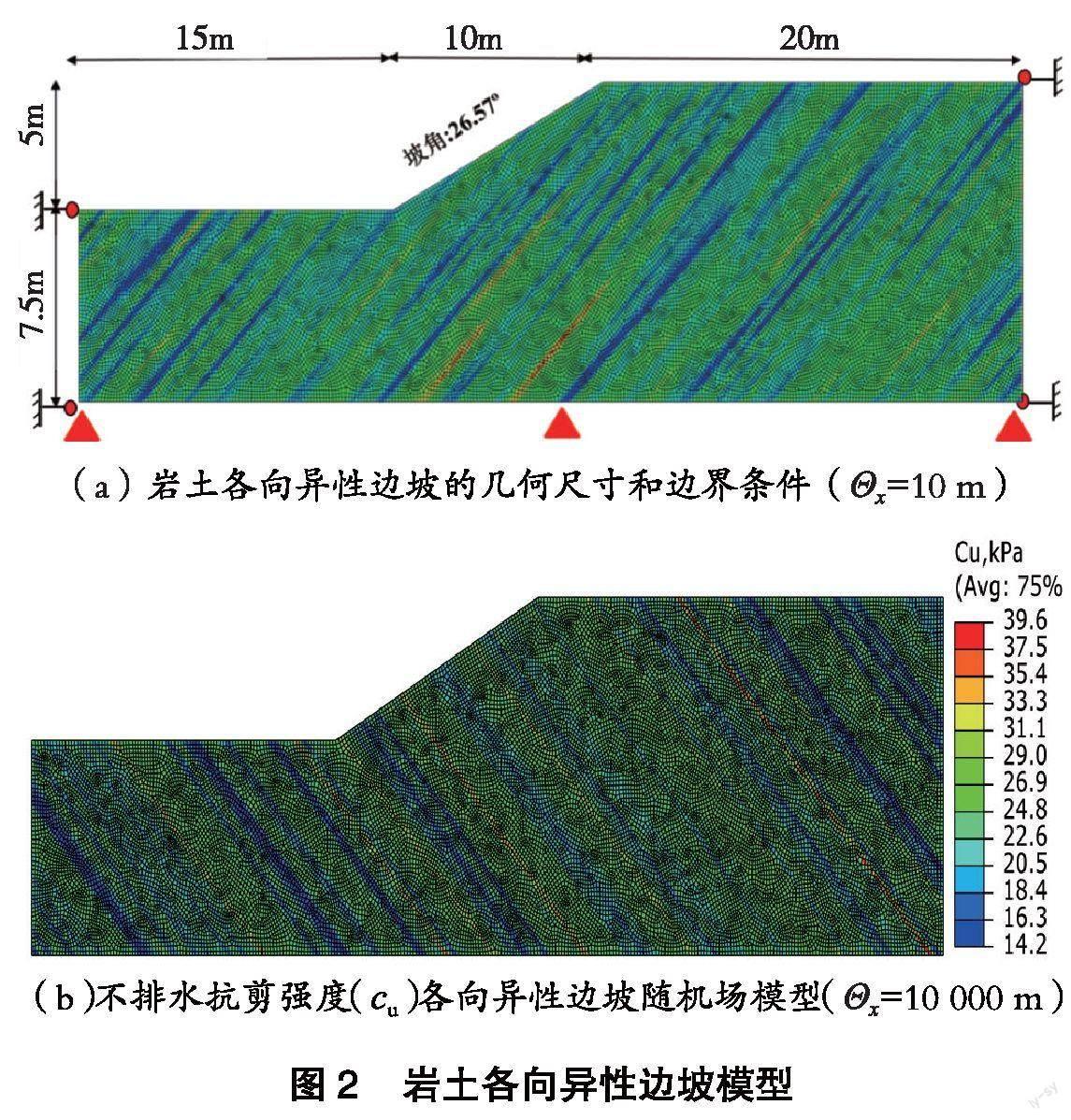
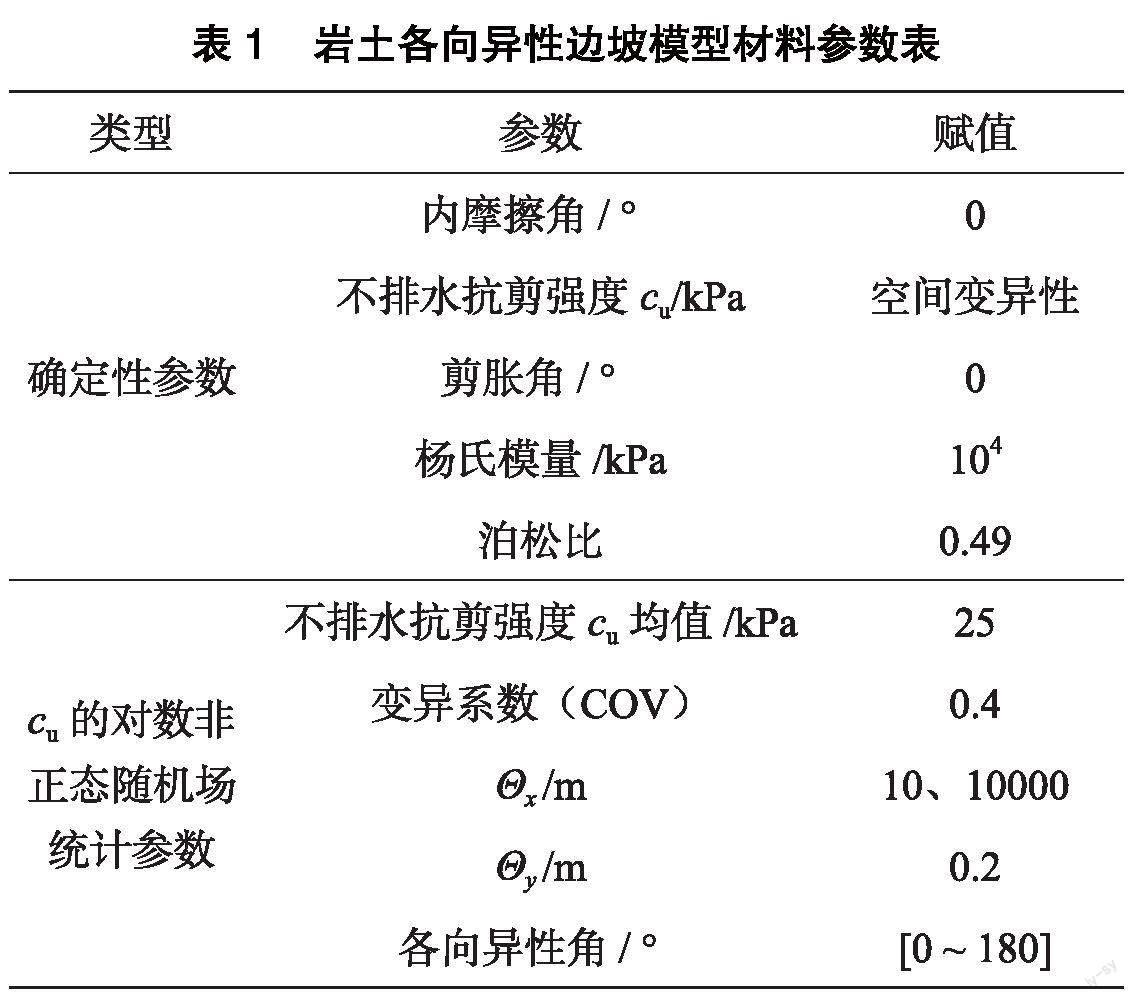
基于随机有限元方法探讨岩土各向异性边坡的破坏模式与稳定性。图2为土体不排水抗剪强度各向异性的边坡模型，该模型由25 976个四节点四面体单元构成，并以对数非正态随机场表征土体不排水抗剪强度[11]（用cu表示）。

目前，模拟非正态随机场主要是按照“两步走”的方法，首先生成正态随机场，然后通过等概率变换产生非正态随机场。本研究中对数正態随机场由改进的线性估计方法产生的高斯随机场转换而来[12]。由于岩土各向异性具有倾向，因此通过修正坐标系推导出岩土各向异性的空间坐标公式

y′ = -xsinβ + ycosβ（1）

x′ = xcosβ + ysinβ（2）

式中：β为旋转角，x和y为旋转之前的坐标。

通过在各向异性方向设置一个主要空间相关长度，在另一个（正交）方向设置一个次要空间相关长度来反演岩土各向异性。沿次要方向的空间相关长度（用Θy表示）设为0.2 m，而边坡中的岩土各向异性可通过沿主要方向较大的相关长度的随机场模型表征。由于天然岩土体很难确定各向异性土层之间的清晰边界（见图1），随机场模型中不同土层之间没有明确的边界之分，不排水抗剪强度（cu） 被认为是每一层土体的关键参数。同时，主方向的空间相关长度（称各向异性分布范围，用Θx表示）可表征各向异性的延伸范围。Zhu等[13]论证了各向异性分布范围对边坡的失稳模式和破坏机理的影响不容忽视，因此考虑Θx=10 m和Θx=10 000 m两个主长度，相对于数值模型尺寸，各向异性分布范围Θx为10 000 m表明模型计算域全部定义为各向异性体。而Θx等于10 m表明土各向异性长度与模型尺寸相似（见图2）。根据莫尔-库仑屈服准则，将土体模拟为理想弹塑性材料，除不排水抗剪强度外，其余材料参数均假定为确定值[14]。

图3为岩土各向异性边坡滑动区域轮廓，灰色单元以上部分区域为边坡的滑动区域。可知，边坡有沿各向异性倾向滑动的趋势，与边坡坡角无关。因此，土体不排水抗剪强度的各向异性对边坡破坏模式影响不容忽视。由于随机场模型从一次模拟（或实现）变到另一次，边坡临界滑裂面也随之改变。因此，针对不同各向异性角和不同各向异性分布范围的组合，每次场景产生200次对数随机场，对岩土各向异性边坡安全系数进行统计分析，综合评估边坡的稳定性。

2 结果与讨论

2.1 各向异性分布范围对边坡稳定性的影响

通过建立6个各向异性角（0°～ 180°）和2个各向异性分布范围（Θx =10 m和10 000 m）的计算模型，综合分析岩土各向异性边坡的安全系数，探究土体各向异性对边坡稳定性的影响。图4为不同各向异性角的边坡安全系数直方图，确定性有限元分析（FEA）在恒定的土体强度为25 kPa下进行。可知，与确定性模式相比（蓝色箭头表示），具有岩土各向异性的边坡安全系数比均匀土体条件下的边坡安全系数小，这是由于岩土各向异性边坡具有沿软弱土层滑动破坏的趋势，而强度较大的其他土层对边坡失稳风险的影响较小。同时，岩土各向异性边坡临界滑裂面（即软弱土层）的强度值小于土体强度均值，边坡破坏所需能量较少，从而导致岩土各向异性边坡的安全系数一般小于均质边坡的安全系数，这表明如果假定土体均匀，则各向异性边坡的稳定性可能被高估，对滑坡危害性的判断出现误差。同时由于岩土各向异性边坡在每次模拟中土体强度较强或较弱区域存在不确定性，从而导致边坡失稳的破坏模式和安全系数具有不确定性，这表明土体各向异性对边坡安全系数有显著影响，在边坡稳定性分析中考虑岩土各向异性很有必要。

由图4可知，Θx为10 000 m的安全系数的波动范围略大于Θx为10 m的波动范围。当Θx较大时，土体相邻区域之间形成较强或较弱土层的可能性较大。最大安全系数和最小安全系数之间的极差是表征一组离散数据波动范围的一个简单指标。从图5可知，Θx为10 000 m的安全系数极差大于Θx为10 m的安全系数极差。因此，各向异性分布范围越大，各向异性边坡安全系数波动范围越大。为了减少岩土各向异性边坡失稳造成的危害，建议考虑无限大的各向异性分布范围对其进行稳定性分析。

2.2 各向异性角对边坡稳定性的影响

由图5可知，各向异性角对安全系数极差有一定影响。当土体各向异性角为26.57°时，岩土各向异性边坡安全系数极差达到峰值。这是因为各向异性角平行于边坡坡角，当软弱土层覆盖坡面时，各向异性边坡有沿坡面滑动破坏的趋势，边坡安全系数较小，而较强土层覆盖于坡面时，边坡安全系数较大。而各向异性角为90°时，安全系数极差达到最小值。

图6为各向异性边坡安全系数均值随各向异性角的演变过程。可知，随着各向异性角的增大，邊坡安全系数先减小后增大再减小，当各向异性角为90°时，边坡的安全系数达到峰值，直立各向异性边坡稳定性略好于水平各向异性边坡。反倾向各向异性边坡（各向异性角大于90°）的安全系数大于顺倾向各向异性边坡（各向异性角小于90°）的安全系数[15]。当各向异性角为45°和135°时，其安全系数分别为顺倾向和反倾向各向异性边坡的最小值。

3 结 论

提出了基于土体不排水抗剪强度各向异性的随机场表征方法，探究了其对边坡的破坏模式和稳定性的影响。主要结论如下。

（1）与均质边坡相比，岩土各向异性对边坡的稳定性有一定影响，均匀土体的假设可能高估了边坡安全系数，在边坡稳定分析中应考虑岩土各向异性。

（2）较大的各向异性分布范围可能产生较大的安全系数波动范围。为了保守估计，在对各向异性边坡进行稳定分析时，建议考虑无限大的各向异性分布范围。

（3）各向异性角为45°和135°的岩土各向异性边坡失稳概率较高。需要指出的是，本研究仅仅考虑土体不排水抗剪强度各向异性对边坡稳定性的影响，但在真实滑坡中内摩擦角的影响不容忽视，需要根据现场调查数据对各向异性边坡的稳定性进行研究。

参考文献：

[1] 郑颖人，陈祖煜，王恭先.边坡与滑坡工程治理（第二版）[M]. 北京：人民交通出版社，2010.

[2] LIU Y，SHIELDS M D. A Direct Simulation Method and Lower-Bound Estimation for a Class of Gamma Random Fields with Applications in Modelling Material Properties[J]. Probabilistic Engineering Mechanics，2017，47：16-25.

[3] XIAO T，LI D Q，CAO Z J，et al. Three-

Dimensional Slope Reliability and Risk Assessment Using

Auxiliary Random Finite Element Method[J]. Computers and Geotechnics，2016，79：146-158.

[4] 程红战，陈健，王占盛，等. 考虑旋转各向异性相关结构的黏土边坡稳定性分析[J]. 岩石力学与工程学报，2017，36（增刊2）：3965-3973.

[5] ZHU H，ZHANG L M. Characterizing Geotechnical Anisotropic Spatial Variations Using Random Field Theory[J]. Canadian Geotechnical Journal，2013，50（7）：723-734.

[6] SINGH P K，SINGH K K，SINGH T N. Slope Failure in Stratified Rocks：A Case from NE Himalaya，India[J]. Landslides，2017，14（4）：1319-1331.

[7] 罗凌晖，周建，蔡露，等.各向异性成层边坡的稳定性分析[J].中南大学学报（自然科学版），2019，50（8）：1883-1890.

[8] HUANG L，CHENG Y M，LEUNG Y F，et al. Influence of Rotated Anisotropy on Slope Reliability Evaluation Using Conditional Random Field[J]. Computers and Geotechnics，2019，115：1-9.

[9] CHEN W F，SNITBHAN N，FANG H Y. Stability of Slopes in Anisotropic，Nonhomogeneous Soils[J]. Canadian Geotechnical Journal，1975，12（1）：146-152.

[10] GRIFFITHS D V，LANE P A. Slope Stability Analysis by Finite Elements[J] Géotechnique，1999，49（3）：387-403.

[11] LIU Y，LEE F H，QUEK S T，et al. Effect of Spatial Variation of Strength and Modulus on the Lateral Compression Response of Cement-Admixed Clay Slab[J]. Géotechnique，2015，65（10）：851-865.

[12] LIU Y，LEE F H，QUEK S T，et al. Modified Linear Estimation Method for Generating Multi-Dimensional Multi-variate Gaussian Field in Modelling Material Properties[J]. Probabilistic Engineering Mechanics，2014，38：42-53.

[13] ZHU H，ZHANG L M. Characterizing Geotechnical Anisotropic Spatial Variations Using Random Field Theory[J]. Canadian Geotechnical Journal，2013，50（7）：723-734.

[14] 田寧，陈健，尤伟军，等.不排水抗剪强度的旋转各向异性非平稳随机场模拟[J].岩土工程学报，2021，43（增刊2）：92-95.

[15] 刘刊，于景宗，杨瑞刚.层状岩体顺向边坡稳定性研究：以大藤峡南木江副坝为例[J].湖南水利水电，2022（5）：62-64.

Probabilistically Quantifying the Effect of Geotechnical Anisotropy on Slope Stability

QI Lei 1，DING Yanan2

（1. Sinohydro Fifth Engineering Bureau Co.，Ltd.，Chengdu 610036，China；2. Changjiang Institute of Survey，Planning，Design and Research Co. Ltd.，Wuhan 430010，China）

Abstract：Due to complex geological processes and loading history，anisotropic geotechnical slopes are widespread in nature. On the basis of the mathematical theory of random field simulation which characterizes rock and soil parameters，the stability of anisotropic slope is examined by stochastic finite element method，Monte Carlo simulation and strength reduction method. Results illustrate that compared to homogeneous soil slopes，anisotropic geotechnical slopes have a relatively low factor of safety. Geotechnical anisotropy affects the damage pattern and stability of slopes. A wider distribution of geotechnical anisotropy generates stronger correlation between soils in adjacent areas and larger potential for landslides. Parallel alignment between anisotropic tendency angle and slope angle leads to a maximum volatility of the range of safety factors. Our findings offer valuable insights for designing reinforcement programs for natural slopes.

Key words：slope stability；geotechnical anisotropy；random fields；factor of safety