采动影响下地面井抽采瓦斯运移影响因素数值模拟研究

唐建平, 李日富

(1.瓦斯灾害监控与应急技术国家重点实验室, 重庆 400037; 2.中煤科工集团重庆研究院有限公司, 重庆 400037)

1 前言

煤炭在我国能源开发及消费中长期占据着主体地位,支撑着经济不断地向前发展,是关系我国国家经济命脉的重要基础产业,在能源消费比重中,煤炭产量占比超过50%,是我国主体能源之一。与之同时,煤炭行业安全形式严峻,煤与瓦斯突出事故是煤矿事故的主要表现形式,强化瓦斯抽采是杜绝突出事故的最根本途径。同时,煤矿瓦斯(煤层气)又是一种优质的清洁能源,是保证能源供应安全的重要部分。采动区地面井瓦斯抽采技术正日趋成熟,广泛运用于全国各大矿井中,是保证瓦斯充分抽采的重要举措之一,地面井瓦斯抽采技术可以实现对煤层采前预抽、采动抽采及采空区抽采进行全范围覆盖,地面井抽采对井下工作面回采几乎不产生影响[1-2]。从目前地面井抽采瓦斯的实际情况观察,实现瓦斯高效抽采仍然是目前急需解决的问题,解决这一问题的关键是弄清瓦斯在煤体中的流动情况及运移规律,从而进行井位的合理布置,进而实现地面井瓦斯的高效抽采。

影响瓦斯运移主要是地应力、渗透率、瓦斯压力等因素[3-4],针对这这些影响因素,众多专家、学者做了大量的研究。李东印[5]将流体流动的主要方程如N-S方程、Brinkman方程和Fick扩散方程运用于煤层工作面及采空区,在考虑有效应力影响的基础上,利用煤体的变形性能建立动态的孔隙率方程,并通过数值模拟软件来反映地面井瓦斯的流动规律。徐剑良和狄军贞等人[6]以地面井煤层气开发中气体滑脱效应、解吸扩散过程和启动压力梯度为变量,在此基础上建立反映煤层气流动的流固耦合数学模型,通过数值软件模拟得到煤层气单井产能。大多数情况下需考虑煤体瓦斯的吸附作用,杨天鸿等[7]建立了含瓦斯煤岩气固耦合模型,并利用该模型探讨了卸压后瓦斯抽采过程。刘延保[8]以统计损伤为理论基础,结合含瓦斯煤岩气固耦合的特点,建立了煤岩损伤本构模型,之后结合瓦斯应力场、浓度场及渗流场,推导出煤岩破裂过程中瓦斯的耦合模型。易俊等[9]在考虑温度影响的情况下,经过室内实验得出煤岩渗透率与温度、应力的表达式,并通过达西定律得出了在温度和地应力作用下的瓦斯渗流方程。

井下工作面的采动及地面井的抽采影响了煤层中的原先的应力平衡状态,主要表现形式的煤体的变形及孔隙率产生变化,煤层瓦斯吸附平衡状态发生改变,吸附于煤层的瓦斯逐渐解吸成游离瓦斯。随着瓦斯抽采的进行,抽采负压在煤层中产生了压差,加剧了煤层瓦斯压力的变化,瓦斯压力的变化必定导致应力场的改变。从另一个角度来看,煤体的渗透率及孔隙率随着应力场的改变而变化,影响着煤层瓦斯的渗流状态。因此,煤层在采动情况下应力场与渗流场存在较强的耦合关系,摸清其耦合规律是研究瓦斯抽采的重要依据之一。

2 数值模型的建立

2.1 数学模型的基本假设

煤体瓦斯流动受到诸多因素影响,在研究过程中,需要对一些次要、影响不大的因素进行简化,在本次研究过程中,需要做如下一些假设[10]:①煤层中瓦斯含量及压力之间的关系服从Langmuir方程;②煤层只存在瓦斯单一气体,其他气体忽略不计;③达西定律可以充分表述瓦斯在煤层中的流动;④煤层视为均质单一的线弹性材料,分布着均匀的瓦斯含量及压力;⑤不考虑温度的影响,均认为是恒温状态。

作为一种裂隙-孔隙双重介质的煤体,游离态及吸附态是存在于煤层之中的两种形式,游离态主要存在于裂隙及较大孔中,而吸附态瓦斯则存于较小孔隙之中。因而瓦斯在煤层中的运动状态也分为两种类型:吸附解吸扩散、渗流状态。根据以上分析可知,煤体的变形及瓦斯的渗流存在耦合关系,如图1所示。

图1 煤体气-固耦合关系图

2.2 动力学模型应力场方程

利用有效应力原理,结合平衡方程、几何方程及本构方程。

可得到的应力场方程见式(1)。

(1)

2.3 采动影响下煤层瓦斯渗流场方程

瓦斯的连续性方程、流动方程、状态方程及含量方程构成了瓦斯的渗流场方程。

煤体是典型的双孔双渗介质,将孔隙气体看作是流向裂隙系统的供给源,从而可得到瓦斯流动的连续性方程为

(2)

(3)

2.4 动态的孔隙率、渗透率模型

在忽略温度影响的情况下,煤体体积变形受到颗粒的吸附及解吸的影响,进而得到煤体孔隙率的表达式为

(4)

(5)

式中,Vs0为原始煤体体积;ΔVs为采动影响下的煤体体积变化;Vp为煤体的总体积;φ0为原始孔隙率;Δp为瓦斯压力的变化量,Δp=P-P0,MPa;εs为单位体积吸附瓦斯的膨胀应力变化情况,吸附应变见式(6)。

(6)

Vm为气体摩尔体积,Vm=22.4×10-3m3/mol。

由此可得到式(7)

(7)

式(8)可表达孔隙率与渗透率之间的数值关系。

(8)

(9)

3 数值模型的建立

3.1 几何模型及参数

将上述建立的应力-渗流耦合数值模型导入COMSOL Multiphysics软件进行模拟,依据软件的计算结果,揭示煤层应力、初始瓦斯压力及初始渗透率对地面井抽采瓦斯的影响,为现场地面井的抽采提供依据。以山西某矿15号煤地面井抽采实践为研究背景,将模型的尺寸设定为100 m×100 m,15号煤厚度6 m,地面井处于模型正中间位置,模型两端对称,为提高计算效率,截取模型其中的1/4体积进行研究,具体如图2所示。对于初始条件的设定,瓦斯抽采负压为20 kPa,温度为303 K。通过对15号煤层基本参数测定、全程取芯物理力学参数测试、工业分析及渗流试验得出模型数值模拟物性参数。

图2 几何物理模型

3.2 初始、边界条件

初始条件和边界条件如下:

(1)煤层原始条件为:t= 0;u=0,v=0。

3.3 数值模拟方案的制定

此次制定3个数值模拟分析方案,共计10个模型,具体模拟方案见表1。方案1,分析不同地应力条件对钻井抽采瓦斯的影响;方案2,分析不同的初始渗透率条件下对地面井抽采瓦斯的影响;方案3,分析不同初始瓦斯压力条件下对地面井抽采瓦斯的影响。此次数值模拟主要分析地应力、初始渗透率及瓦斯压力对地面井煤层气开发效率的影响,煤层的各项物性参数见表2。

表1 数值模拟方案

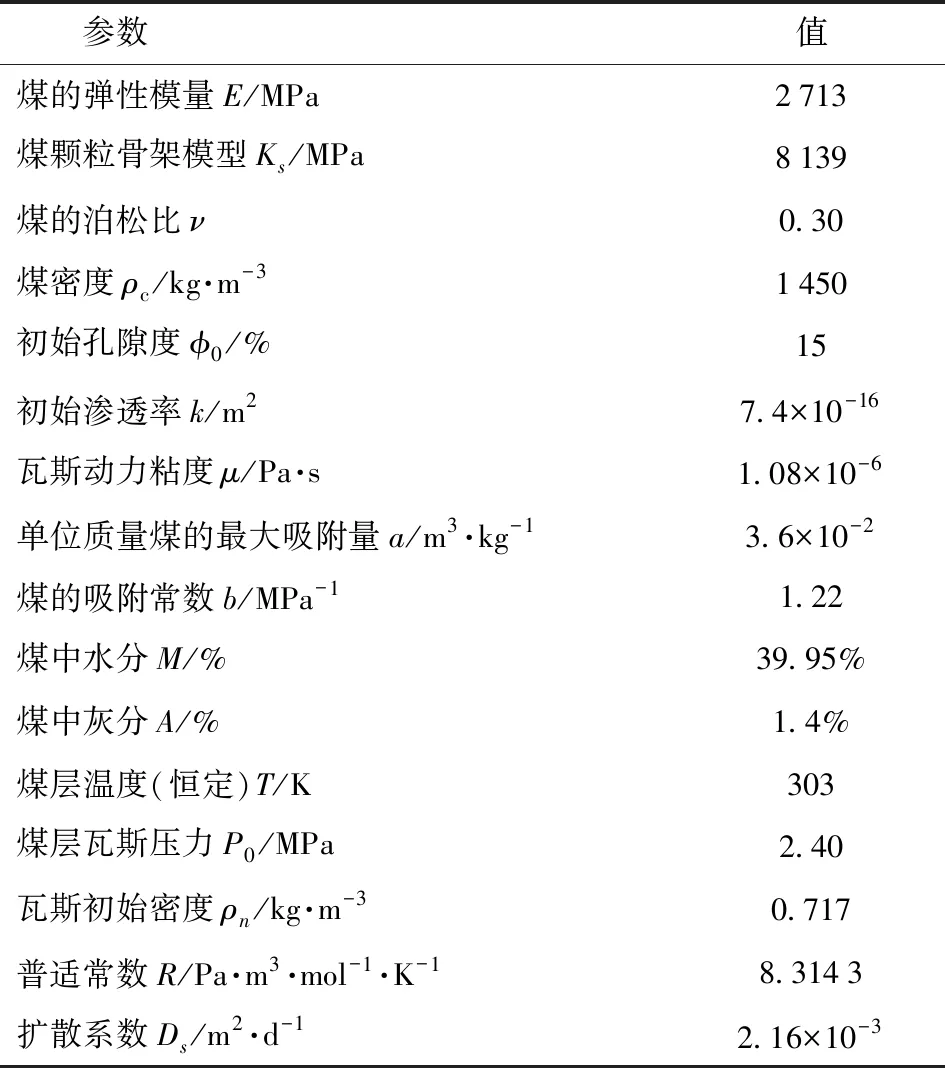
表2 模型数值模拟物性参数

4 数值模拟结果分析

4.1 地应力对抽采的影响

地应力是煤层重要的物性参数之一,不同赋存状态的煤层所受的地应力不同,对于采动地面井抽采瓦斯有极为关键的作用。此次模拟方案参照方案一。原始瓦斯压力设定为2.4 MPa,原始渗透率设定为7.4×10-16m2,按照方案一上覆边界的压力设定为-3 MPa、-6 MPa、-10 MPa,地面井抽采时间设定为1 000 d,分析在此条件和时间下煤层各参数的变化情况,分析不同的地应力条件对地面井抽采的影响,具体瓦斯压力分布云图如图3所示。

图3 不同地应力条件下地面井抽采1 000 d后煤层瓦斯压力分布云图

从上述图3不同地应力条件下地面井抽采1 000 d后煤层瓦斯压力分布云图可以看出,在不同的应力分布条件下,地面井抽采瓦斯压力的分布具有相同的分布规律。为了进一步分析在该地应力分布条件下地面井抽采影响范围内孔隙率及渗透率的变化情况,在该模型中选取A(0,0,3)和B(50,50,3)两点连成一条线,并在该线上选取另外三个点C(2,2,3)、D(5,5,3)和E(20,20,3),布置如图4所示。

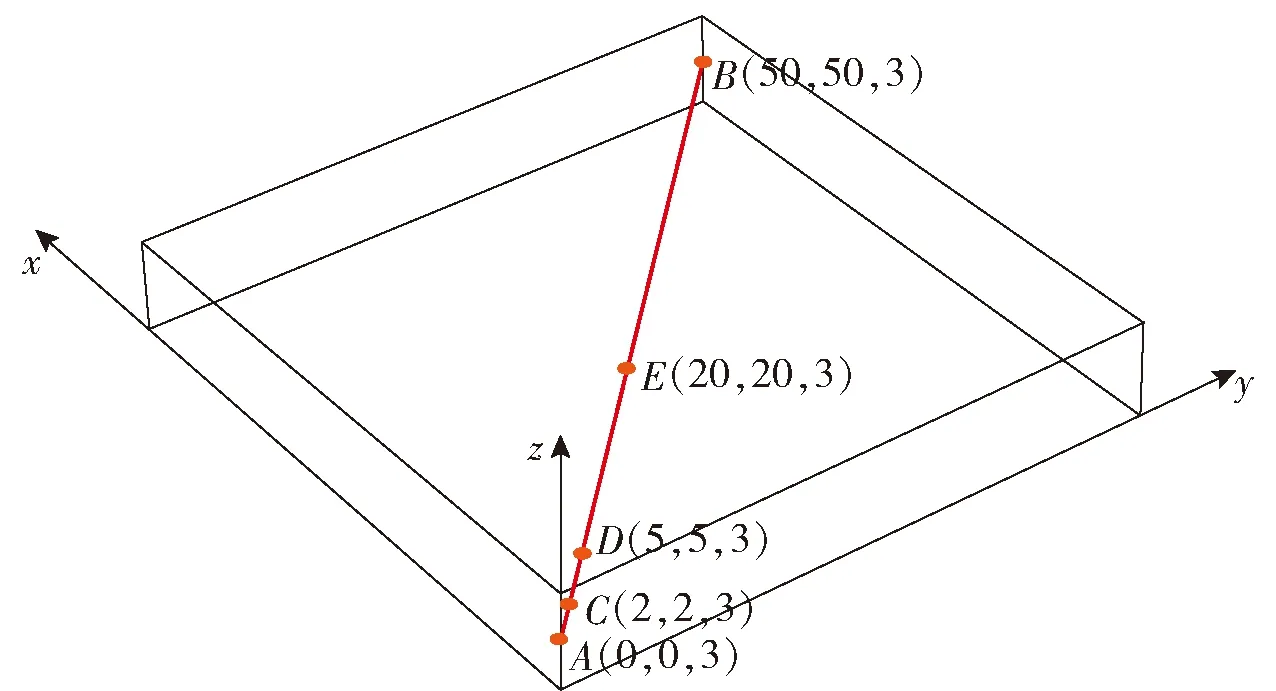
图4 考察线及点布置图

之后以上覆应力6 MPa为例来反映各参数的变化,在C、D、E点中瓦斯压力、孔隙率及渗透率随时间的变化如图5、图6所示。

图5 Fz=-6 MPa条件下对角线煤层瓦斯压力随时间变化图

图6 Fz=-6 MPa情况下不同位置孔隙率、渗透率差异图

由图5可知,随着地面井抽采瓦斯的进行,周边受到地面井的影响范围在不断扩大,但瓦斯压力增加幅度在减小。当抽采时间到100 d时,选定地面井10 m的影响范围,该瓦斯压力较地面井中心增加了0.82 MPa,而影响范围10～20 m较10 m增加了0.16 MPa,20～30 m较影响范围10～20 m增加了0.09 MPa,随着影响范围的进一步扩大,瓦斯压力变化的幅度值在不断下降。

在地应力为6 MPa,离地面井不同距离的渗透率及孔隙率随时间和瓦斯压力变化情况如图6所示,由图6可以看出,孔隙率及渗透率随着抽采时间的增加先减小,而后增大,其中瓦斯压力1 MPa时为临界点。当初始瓦斯压力从2.4 MPa降低到1.0 MPa时,煤层渗透率、孔隙度同步减小;当瓦斯压力降低到1 MPa以下时,孔隙率及渗透率开始增大。根据有效应力原理可知,气体压力的减小会导致有效应力的增加,从而引起介质骨架发生变形,进而使孔隙率、渗透率变小。但随着后续瓦斯抽采的不断进行,瓦斯压力下降到一定程度后,煤体瓦斯吸附膨胀变形减小,因而出现一定程度上渗透率及孔隙率的增大。

4.2 初始渗透率的不同对地面井抽采瓦斯的影响

渗透率是影响煤层瓦斯抽采的关键性因素,渗透率的大小直接决定煤层瓦斯在防突过程中的消突和煤层气开采的产量,为了分析不同初始渗透率抽采条件下煤层气开采效果,设计模拟方案如方案2,模拟所取原始瓦斯压力2.4 MPa、上覆应力为-6 MPa,将初始渗透率分别设定为7.4×10-15m2、7.4×10-16m2及7.4×10-17m2,抽采时间设为t=1 000 d。

初始渗透率的不同对瓦斯抽采的影响如图7所示,从图中可以看出,在不同初始渗透率条件下,最大残余瓦斯压力有所不同,设定的初始瓦斯压力均为2.4 MPa情况下,当初始渗透率为7.4×10-15m2时,经地面井一段时间抽采过后,剩余的残余瓦斯压力为0.44 MPa;当初始渗透率为7.4×10-16m2时,剩余的残余瓦斯压力为0.98 MPa,约为渗透率7.4×10-15m2时的2.2倍;当初始渗透率为7.4×10-17m2时,残余瓦斯压力为1.59 MPa,约为初始渗透率7.4×10-16m2时的1.62倍,为初始渗透率7.4×10-15m2的3.6倍,煤层初始渗透率的对地面井的抽采效果起到了重要作用。图7(b)所示为相同抽采时间、不同初始渗透率条件下,煤层气抽采量最终的产量累计值。由图可知,当初始渗透率为7.4×10-15m2时,抽采产量最终值为2.98×105m3;当初始渗透率为7.4×10-16m2时,抽采产量最大值为0.91×105m3,为前者的30.53%;当初始渗透率为7.4×10-17m2时,抽采产量的最终值为0.38×105m3,是k0=7.4×10-16m2的42%,是k=7.4×10-15m2时的13%。由图7(c)可以清楚地看出当初始渗透率为7.4×10-15m2时,其抽采速率分别是7.4×10-16m2和k0=7.4×10-17m2的6倍和12倍,但随着抽采的不断进行,在瓦斯压力降低的同时,抽采效率亦开始下降。从图中可以得出,采动影响下,初始渗透率对地面井瓦斯抽采影响明显,初始值越大,瓦斯压力下降越显著,抽采速率和抽采量同时变大。因而在地面井进行抽采时,提高煤层初始渗透率不失为实现钻井高效抽采的一种方法。

恩格斯主张站在辩证唯物主义和历史唯物主义的立场考察社会历史条件，进而对文学现象做出评价，并提出文学批评所依据的尺度和标准是“美学观点和历史观点”这一“非常高的，即最高的标准”[6]586。在笔者看来，所谓“历史的标准”不仅意味着在具体的历史情境中评价文学作品，而且意味着将文学作品置于文学发展历程中加以考察，唯有如此，才能发现作品在艺术上的独创之处，得出公允确当的结论。令人赞赏的是，尚继武非常重视在文学发展与变迁的历史中考察《聊斋志异》的叙事艺术，沿着三条“历史之线”分析论述相关问题。

图7 初始渗透率的差异对瓦斯抽采的影响

4.3 初始瓦斯压力对地面井抽采的影响

由图8(a)可以很明显地看到,在抽采时间同为1 000 d的情况下,设定的初始瓦斯压力2 MPa、3 MPa、4 MPa、6 MPa分别降至0.88 MPa、0.96 MPa、1.04 MPa、1.06 MPa,虽然瓦斯压力初始值越大,降低幅度越大,但最终的残余瓦斯压力差异不大。从图8(b)可看出,虽处在不同初始瓦斯压力情况下,经过一段时间抽采后,渗透率都会稳定在一个固定值。根据图8(c)及图8(d)可看出,初始瓦斯压力越大,瓦斯抽采速率及累计抽采量越大,钻井抽采速率与瓦斯压力初始值直接相关,初始值大,开始的渗流速度也快,但经过1 000 d时间的抽采,不同初始瓦斯压力条件下,但最终抽采速率及残余瓦斯压力都几乎稳定在一个数值上,但最终的剩余瓦斯压力差异不大。

图8 不同初始瓦斯压力下煤层各参数的变化

通过以上的数值模拟结果可知,地面钻井瓦斯抽采速率及抽采量受地应力、瓦斯压力、渗透率影响明显,其中渗透率是其决定性参数,但渗透率主要受到了地应力的影响。

采动影响区地面井试验工程为该矿3304工作面,工作面埋深350～410 m,15号煤层原始瓦斯压力为0.19～0.72 MPa,平均原始瓦斯含量11.49 m3/t,根据现场实际观测,钻井距回采面100 m时平均瓦斯浓度为11.8%,平均瓦斯纯量为0.14 m3/min;30 m距离时平均瓦斯浓度为50.6%,平均瓦斯纯量1.88 m3/t;10 m距离时平均瓦斯浓度为81.3%,平均瓦斯纯量为3.59 m3/t。从中可以看出,受到工作面采动的充分影响,煤层渗透率得到极大的提高,抽采浓度及纯量皆有阶跃式地增长,极大地提升了地面井抽采效率。

5 结论

(1)建立了采动影响下含瓦斯煤体的多物理场的耦合数学模型,推导出了煤体应力及渗流方程,进而得出孔隙率及渗透率与应变、瓦斯压力等参数之间相互关系。

(2)以山西某矿为工程背景,利用COMSOL Multiphysics软件对地面井瓦斯抽采实践进行模拟,并确立了数值模拟的初始和边界条件,分析不同地应力条件、不同的初始渗透率及不同初始瓦斯压力对钻井抽采产量及效率的影响。

(3)通过数值模拟结果可知,地面钻井瓦斯抽采速率及抽采量受地应力、瓦斯压力、渗透率影响明显,其中渗透率是其决定性参数,但渗透率主要受到了地应力的影响。在一定地应力条件下,孔隙率及渗透率随着抽采时间的增加先行减小,而后增大,存在着一个临界残余瓦斯压力点;而初始渗透率对地面井瓦斯抽采影响明显,初始值越大,瓦斯压力下降越显著,抽采速率和抽采量同时变大。因而在地面井进行抽采时,提高煤层初始渗透率不失为实现钻井高效抽采的一种方法。

(4)通过采动地面井现场实际试验表明,受到采动充分卸压以及渗透率的提高影响,抽采浓度及纯量皆有阶跃式地增长,极大地提升了地面井抽采效率。