几何路径跟踪组合算法及其农业机械自动导航应用

崔鑫宇，崔冰波，2*，马振，2，韩逸，张建鑫，魏新华，2

（1. 江苏大学农业工程学院， 江苏镇江， 212013；2. 江苏大学现代农业装备与技术教育部重点实验室， 江苏镇江， 212013）

0 引言

农业机械（简称农机）自动导航是农机装备智能化重要体现，也是缓解劳动力短缺、实现精准农业的有效途径［1-4］。农机自动导航系统主要包括运动感知、路径规划以及路径跟踪控制等模块，其中高精度路径跟踪控制是农机可靠自主作业的重要保证［5-6］。

为改善农机路径跟踪稳定性，采用模型无关路径跟踪控制可以避免参数辨识，并减少时变参数引入的控制误差［7-8］。典型模型无关路径跟踪方法包括PID算法和纯追踪算法（pure pursuit， PP）［9］，其中PP 是模拟人类驾驶习惯而建立的轨迹跟踪方法，其较PID 算法具有实施简单、待调参数少等优势，在低速移动载体自动驾驶中应用广泛［10-11］。前视距离是PP 算法唯一可调节参数，为提高PP 算法自适应性，许多学者采用在线优化算法动态更新前视距离［12-14］。 然而COULTER［15］指出PP 前视距离与路径曲率不存在仿射变换，即某一路径曲率可能对应多个前视距离。此外常规PP 算法未考虑速度较快时曲率突变、转向执行器饱和及时滞影响。肖世德等［16］提出两阶段PP 算法解决执行器饱和问题，其实质为利用两阶段车辆跟踪状态动态更新前视点，WANG 等［17］采用双前视点PP和大增益控制方法组合，解决转向执行器时滞和大跟踪误差导致的上线速度较慢问题。

为克服PP 算法收敛速度慢和模型参数需在线优化的缺点，研究利用几何路径跟踪组合算法具有独特优势。Stanley 模型是车辆自动驾驶常用路径跟踪算法，其采用非线性反馈函数使得横向跟踪误差指数收敛于零［18］。课题组前期试验结果表明Stanley 模型在初始误差较大时上线距离较短，适用于大跟踪误差快速上线，但其在变曲率路径跟踪中仍存在稳态跟踪误差问题［19］。为改善Stanley 模型适应性，学者们相继采用模糊控制、群体智能等算法自适应调整不同误差和路径曲率条件控制增益系数［20］。

受两阶段和双前视点PP 算法启发，提出一种融合Stanley 模型与PP 算法的组合算法实现农机连续地头转弯自动导航作业。对于直线路径低速行驶场景采用固定前视距离PP 算法，而对地头转弯和初始上线阶段采用Stanley 模型进行路径跟踪。采用移动小车平台对农机作业常见的U 型路径、梭行路径进行自动导航验证。

1 自动导航系统结构

为验证路径跟踪算法有效性，搭建如图1 所示自动导航系统验证平台，主要包括RTK 流动站接收机、导航工控机以及STM32 单片机，小车移动底盘集成编码器、CAN 总线和转向电机。RTK 流动站板卡采用和芯星通UM482 定位模块和华信贴片式数传电台自主研发，平面定位精度为1 cm+1 ppm（1 ppm 表示离基站每超过1 km 定位误差增大1 mm），1 m 基线长度配置下定向精度为0.2°，其以5 Hz 实时输出定位与定向信息，RTK 定位基站接收机内置NovAtel OEM719板卡。

图1 自动导航系统验证平台Figure 1 Platform for automatic navigation system verification

移动小车自动导航流程图如图2 所示，其中上位机导航决策软件实时获取移动小车位置与航向，通过在预规划路径上进行索引点更新计算导航偏差，并将导航偏差与前视距离、增益系数、直线/曲线标志位发送至STM32 单片机。

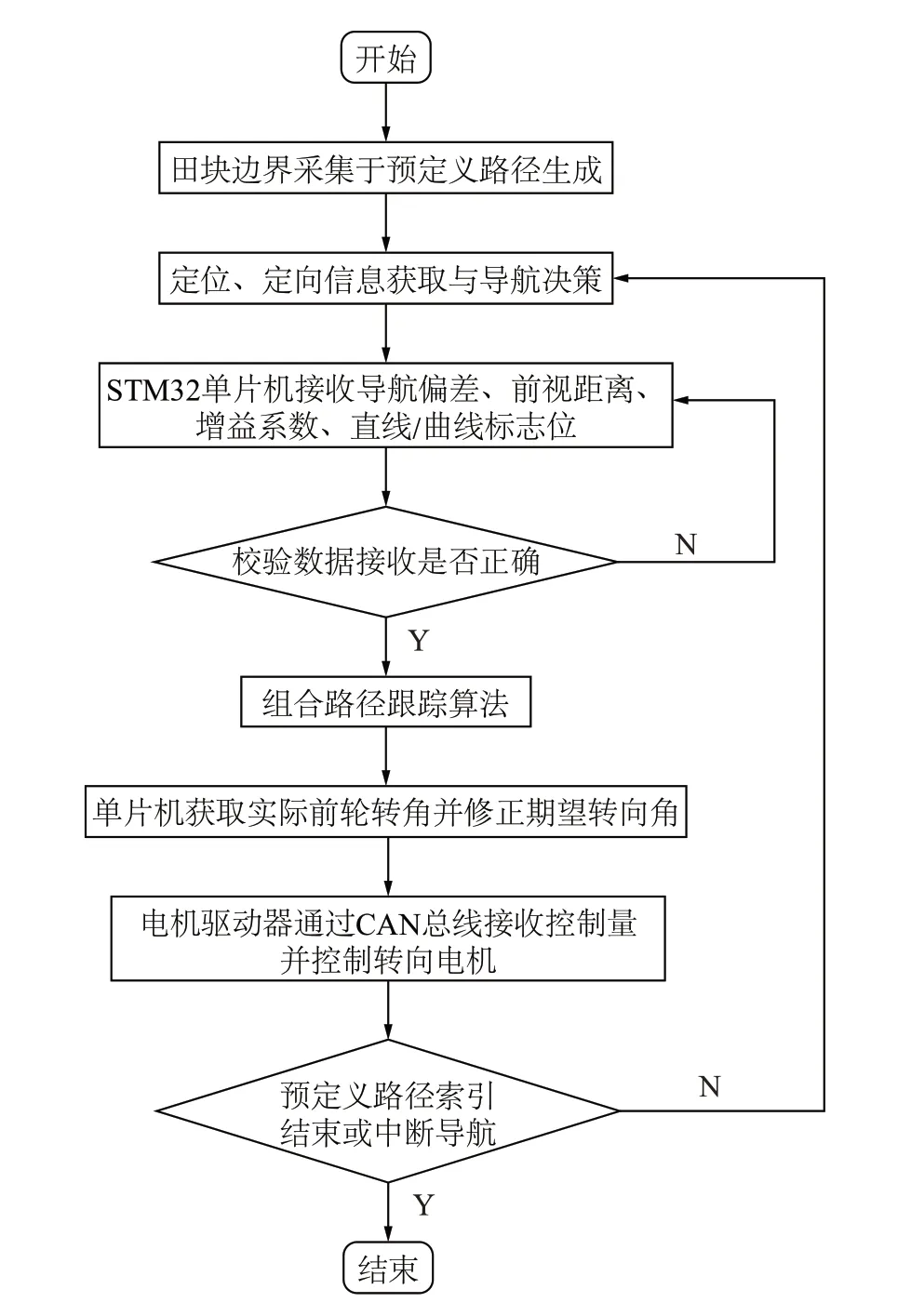
图2 移动车辆自动导航流程图Figure 2 Flowchart of automatic navigation for mobile vehicle

单片机根据路径标志、偏差信息进行路径跟踪算法切换，并由导航偏差、增益系数或前视距离计算期望转向角。单片机通过CAN 总线以频率5 Hz 将控制信息发送至电机驱动器，实时接收编码器输出前轮转角构造行驶控制闭环系统，电机驱动器将控制信息转换为电压值并以100 Hz 频率控制转向电机。

2 几何路径跟踪原理

2.1 车辆运动学建模

农机在田间低速作业时，线性化转向控制系统与轮胎接触模型满足阿克曼转向模型，其二轮车运动学模型如图3 所示。规定拖拉机的航向角φ、前轮转角δ、控制点侧偏角γ逆时针方向为正。H点为控制参考点，其在XOY平面坐标为（xb，yb），到后轴中心的距离为Lt，当H点位于后轴中心处γ为0。

图3 车辆二轮车模型示意图Figure 3 Schematic of vehicle bicycle model

由运动学关系可得：

式中：L——前后轮轴距，m；

γ——控制点侧偏角，rad；

φ——车身航向角，rad；

δ——前轮转向角，rad；

v——车辆速度，m/s；

ω——车辆角速度，rad/s。

2.2 纯追踪模型

PP 算法是一种模型无关的几何路径跟踪算法，其主要根据当前车辆定位中心、车身航向和目标点位置来确定行驶控制圆弧轨迹，PP 算法模型如图4 所示。

图4 纯追踪模型示意图Figure 4 Schematic of pure pursuit model

基于前视距离Ld可选择车辆行驶目标点P，定义该点与车辆后轴中心（定位中心）连线与车身航向夹角为α，通过计算圆弧曲率k得到转向控制量。设前视点P在车辆坐标系中的坐标为（x，y），R为车辆当前转角下转弯半径，C为圆弧圆心，由几何关系可得

综合式（4）～式（6）可得

式中：k——后轴中心轨迹曲率。

根据车辆模型几何关系可得

式中：δ(t)——前轮转向角，rad。

因此PP 模型控制量表达式如式（9）所示。

2.3 Stanley 模型

Stanley 模型命名来自于斯坦福大学自动驾驶车辆团队，该团队在2005 年DARPA 举办的无人车挑战赛中获胜［18］。Stanley 模型基于前轴中心路径跟踪偏差量，对方向盘转向控制量进行计算，能够较好的跟踪转弯路径，且车辆快速行驶时也能获得稳定跟踪效果，其算法模型如图5 所示。

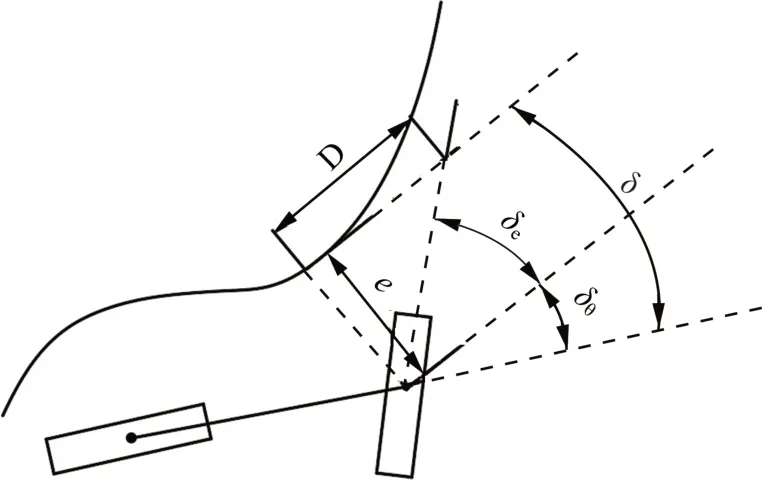
图5 Stanley 模型示意图Figure 5 Schematic of Stanley model

Stanley 模型前轮期望转角由两部分组成，分别为航向偏差引起的转角（车身方向与参考轨迹最近点切线方向的夹角）、横向偏差引起的前轮期望转角（前轴中心到参考轨迹最近点的横向距离），其表达式：

式中：δ(t)——前轮期望转角，rad；

δe(t)——横偏引起的期望转角，rad；

δθ(t)——航偏引起的期望转角，rad。

只考虑横向偏差影响时，前轮期望转角随横向偏差增大而增大，预瞄点在距离前轮路径投影点D处。

由几何关系得

式中：K——增益系数；

e(t)——横向偏差，m；

θe(t)——横向偏差引起的角度，rad；

v(t)——行驶速度，m/s。

单独考虑航向偏差影响时，前轮转角等于车辆航向与最近路径点切线方向之间的夹角。

式中：θθ(t)——航向偏差，rad。

同时考虑航向偏差及横向偏差引入的期望转角，可得Stanley 模型的控制量表达式为

3 算法分析与验证

农业机械田间作业路径包括直线路径、曲线路径以及上线路径，本节通过分析Stanley 模型和PP 两种算法在U 型路径下的优缺点，得到两种几何路径跟踪算法误差特性，进而基于其优化参数进行跟踪算法组合，并将组合算法用于U 型路径与梭行作业路径跟踪验证。

3.1 路径规划方案

U 型转弯路径主要输入参数为直线端点坐标、最小转弯半径以及作业幅宽，详细路径生成见文献［6］。农机田间全覆盖作业要求农机沿路径行驶时能够遍历田块可作业区域，常用往复式梭行作业路径如图6 所示，其作业路径包括直线作业区域和地头转弯区域，在获取田块可作业区域长度与宽度后，根据机具作业幅宽、最小转弯半径以及起始点信息即可生成连续多个U 型路径。设定直线作业区域与地头转向区域交点为机具提升控制标记点，根据此标志点可进行路径跟踪算法切换。

图6 往复式梭行作业路径示意图Figure 6 Schematic of boustrophedon path

3.2 路径跟踪算法特性分析

为对比两种几何路径跟踪算法误差特征，采用移动小车在江苏大学耒耜楼一楼广场进行农机U 型路径跟踪试验，测试过程卫星信号和差分校正信号正常。试验场地为水泥路面，小车无打滑现象，控制小车的直线行驶平均速度约为1.0 m/s，曲线行驶平均速度约为0.7 m/s。

设置初始横向偏差为2.5 m，转弯半径为5.0 m，对比两种算法不同参数针对于U 型路径的跟踪性能。Stanley 模型路径跟踪结果如图7 所示，由图可知K=0.65 时跟踪效果最好，其最大偏差为6.0 cm，平均偏差为-1.7 cm，标准差小于2.5 cm。PP 路径跟踪结果如图8 所示。

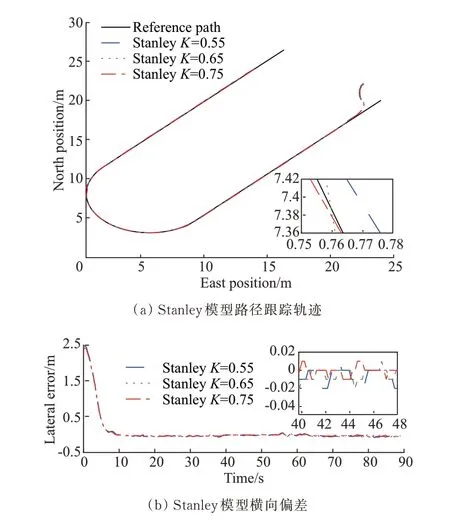
图7 Stanley 模型路径跟踪Figure 7 Path tracking result of Stanley model

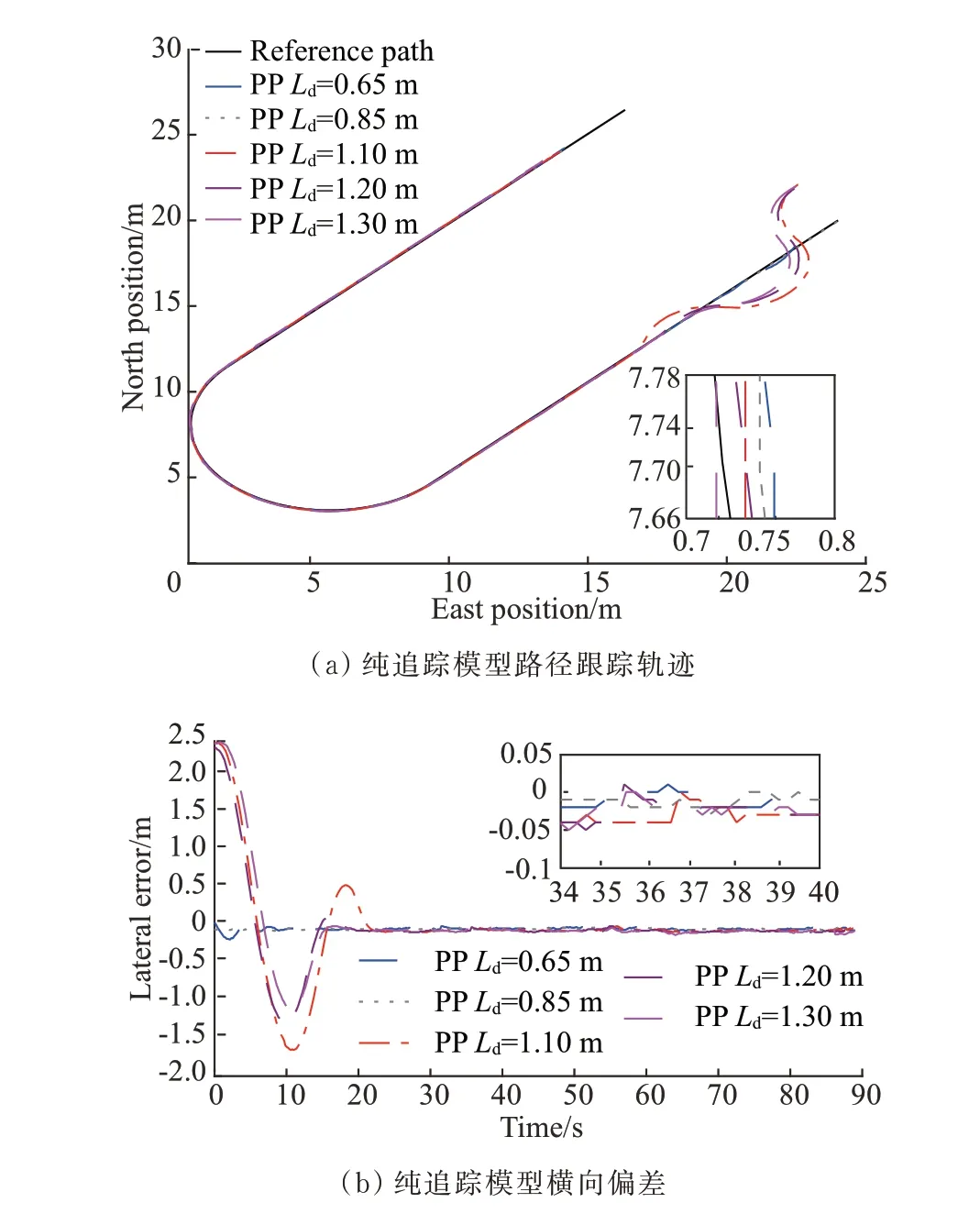
图8 纯追踪模型路径跟踪Figure 8 Path tracking result of pure pursuit model

Ld较小时其上线距离较长且存在较大震荡，设置初始横向偏差为较小值进行误差分析，当Ld=0.85 m时，最大偏差为6.0 cm，平均偏差为-1.9 cm，标准差小于2.0 cm。Ld较大时设置初始横向偏差为2.5 m，当Ld=1.3 m 其跟踪效果较好，具体跟踪误差如表1所示。

表1 几何路径跟踪算法结果Table 1 Result of geometric-based path tracking algorithms

3.3 组合路径跟踪算法验证

由前文可知，前视距离较大导致PP 横向偏差收敛过程缓慢，曲线路径跟踪时会提前转弯不能很好跟踪路径。前视距离小可以减小路径跟踪稳态误差，但抗干扰能力较差，造成震荡。增益系数决定Stanley 模型横向偏差对车轮转角的决策量权重，大增益系数可以快速减小横向偏差，使车辆较好跟踪曲线路径，同时改善直线路径跟踪稳态精度。航向偏差和横向偏差对车轮期望转角的影响具有方向性，当偏差方向相同时前轮期望转角会很大，当偏差方向相反时前轮期望转角会较小。因此，本文提出一种组合算法即：上线过程采用Stanley 模型，直线跟踪过程中采用PP 算法，跟踪曲线路径时切换回Stanley 模型。

3.3.1 组合跟踪算法切换

组合跟踪算法流程见图9。

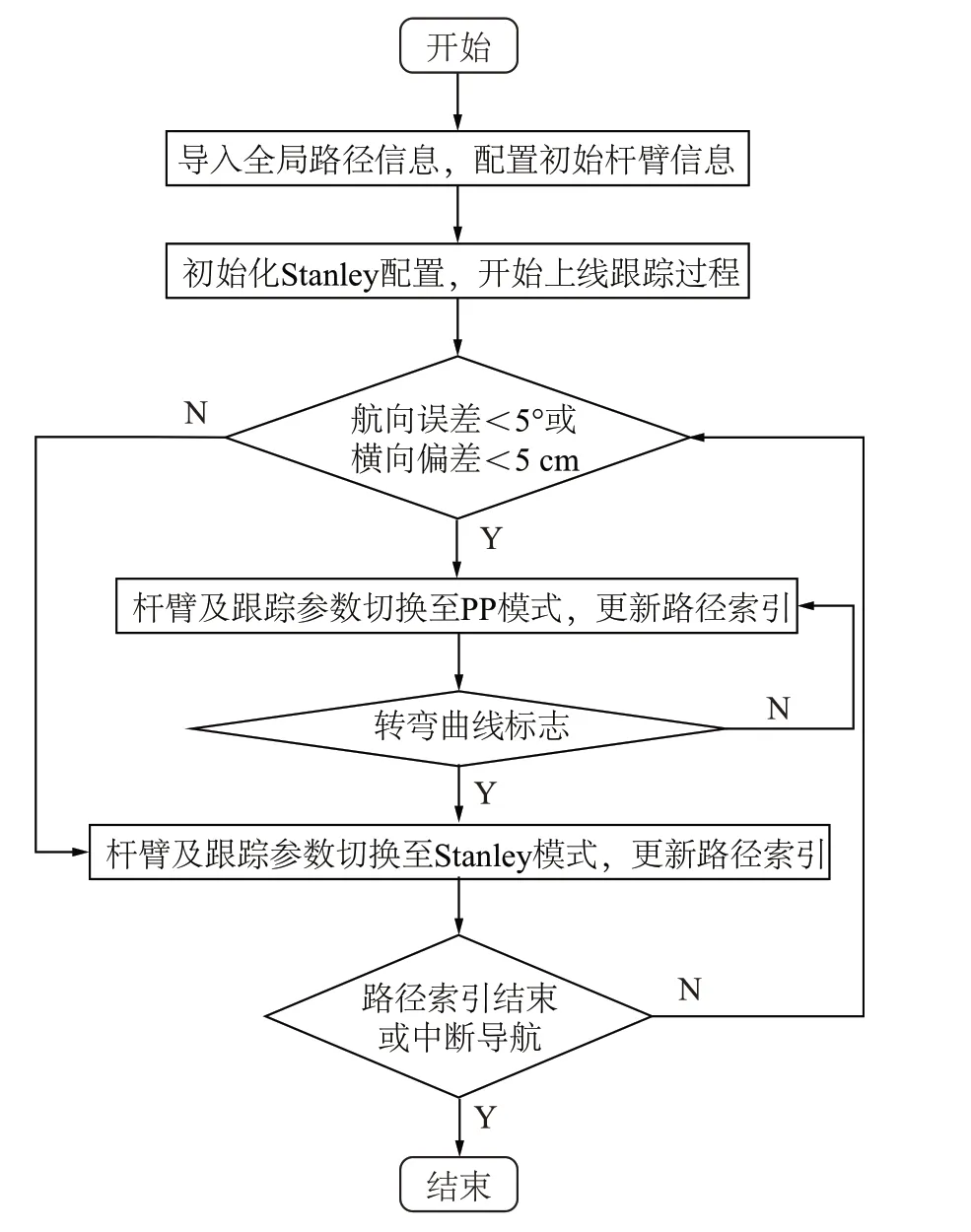
图9 组合跟踪算法流程图Figure 9 Flowchart of integration path tracking algorithm

两种路径跟踪决策模型中车辆控制参考点不同，Stanley 模型将控制中心设置在前轴中心，而PP 是将控制中心设置在后轴中心，因此上位机需要根据实时情况来调整杆臂配置控制参考点。在路径跟踪过程中，上位机同时输入Stanley 增益、PP 前视距离参数、直线/曲线标志位至下位机。在上线过程中，下位机默认跟踪算法Stanley，当横向偏差<5 cm 或航向偏差<5°时，组合算法自动切换为PP 算法。上线后下位机根据路径类型标志位进行判断，当直线路径跟踪时执行PP，当曲线跟踪时执行Stanley 模型。由于直线曲线切换，导致定位信息突变，造成组合算法跟踪偏差突然变化，后续工作中加入卡尔曼滤波可以解决此问题。

3.3.2 U 型路径组合算法验证

为验证算法准确性，在江苏大学进行试验。小车初始横向偏差2.5 m，直线跟踪平均速度为1.0 m/s，曲线路径跟踪平均速度为0.7 m/s，试验结果如图10和表2 所示。

表2 不同算法U 型路径跟踪结果Table 2 U-shaped path tracking results of different algorithms

图10 不同算法路径跟踪Figure 10 Path tracking result of different algorithms

组合算法相对于PP 上线距离减小40.6%，最大横向偏差与Stanley 和PP 分别减少12.5% 和30.0%。组合算法平均偏差相对于Stanley 和PP，分别减少28.6%和57.4%。图11 为组合算法上线后横向偏差频次分布图，其横向偏差87.3%稳定在±5.0 cm。

图11 U 型路径组合跟踪横向偏差频次分布图Figure 11 Error frequency histogram of integration path tracking for U-shaped path

3.3.3 梭行路径组合跟踪算法验证

为模拟农机田间全田块作业轨迹，以自动导航小车为测试平台，采用梭行路径方式进行轨迹跟踪试验。转弯半径约5.0 m，初始横向偏差约2.5 m，直线跟踪平均速度约1.0 m/s，曲线跟踪平均速度约0.7 m/s。梭行路径跟踪轨迹图与横向偏差结果如图13～图14及表3 所示。

表3 不同算法往复式梭行路径跟踪结果Table 3 Result of different algorithms for boustrophedon path tracking

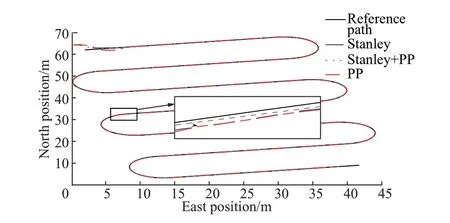
图13 往复式梭行路径跟踪轨迹Figure 13 Path tracking result of boustrophedon path

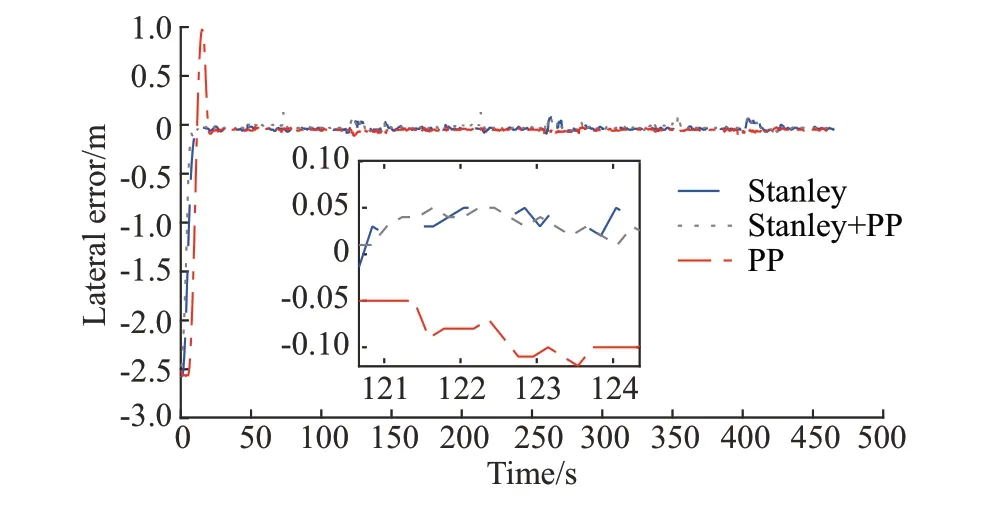
图14 往复式梭行路径跟踪横向偏差Figure 14 Lateral error of boustrophedon path tracking

组合算法平均偏差相对于Stanley 和PP，分别减少36.8% 和54.7%，最大偏差分别减少18.2% 和25%。图15 为组合算法上线后横向偏差频次分布图，可知横向偏差91.7%稳定在±5.0 cm。

4 结论

为改善农业机械路径跟踪算法的适应性，采用模型无关的几何路径跟踪组合算法来实现不同路径曲率和初始误差条件下农机路径跟踪。通过对比分析纯追踪算法和Stanley 模型在U 型路径跟踪中的优缺点，以跟踪误差和路径曲率为变量设计路径跟踪组合算法切换逻辑。通过搭建自动导航系统，并以农机作业常用的往复式梭行路径对算法进行验证，相关结论如下。

1）U 型路径跟踪试验结果显示PP 模型在直线路径跟踪过程中跟踪精度较高，Stanley 模型在初始横向偏差较大场合具有更短上线距离，且转弯曲线跟踪过程稳态误差较小。往复式梭行路径跟踪结果表明，几何路径跟踪组合算法最大偏差较纯追踪和Stanley 分别减小25.0%和18.2%，并在整个路径跟踪过程中有91.7%的跟踪误差小于5.0 cm，满足农业机械全田块路径跟踪精度与稳定性需求。

2）试验结果表明，根据路径跟踪算法误差特征设计组合算法切换逻辑切实可行，其有效减少几何路径跟踪算法参数在线优化运算量和复杂度。本文对单一农机作业场景中速度和路径曲率变化进行试验，结果表明其能够改善农机路径跟踪适应性和稳定性。由于农机自动导航场景中路径曲率和作业速度可以事先定义或枚举，采用几何路径跟踪组合算法为复杂场景中自适应路径跟踪算法设计提供了工程实现参考。

3）本文通过对比分析纯追踪和Stanley 模型的误差特征，基于模型无关路径跟踪控制算法提出几何路径跟踪组合算法。该算法有效地提高了农业机械路径跟踪精度和稳定性，满足农业机械全田块路径跟踪实际需求。本文组合算法路径跟踪结果未考虑切换瞬间参考点突变影响，且受移动小车转向执行机构加工误差影响，路径跟踪组合算法存在稳态误差，下一步将围绕车身位姿信息抗差估计和转向系统参数辨识开展研究，进一步提升农机自动导航系统适应性。