基于CRITIC-熵权法的桥梁地震风险多尺度评估

谢皓宇, 牛松山, 郑万山, 唐光武, 仉文岗

(1. 招商局重庆交通科研设计院有限公司 桥梁工程安全与韧性全国重点实验室,重庆 400067;2. 重庆大学 土木工程学院,重庆 400045)

0 引 言

交通系统是城市居民日常生活与经济活动的重要的生命线。近年来,由于交通技术发展以及城市区域的不断扩张,道路系统与桥梁网络正变得愈加复杂,而桥梁结构通常被认为是交通系统基础设施运营维护安全中最脆弱的一环。20世纪以来全球发生的诸多地震灾害显示,由于桥梁工程遭到严重破坏而切断了震区交通生命线,造成救灾工作的巨大困难并使次生灾害加重,导致巨大的经济损失[1]。因此,评估桥梁网络的震灾防御性能,并制定相应加固优先级策略显得十分关键。

我国早期的桥梁抗震设计规范由于要求偏低或规定不够细致等原因,1990年以前修建的桥梁在抗震设计方面可能存在不同程度的问题,现行的CJJ 166—2011《城市桥梁抗震设计规范》和JTG/T 231-01—20《公路桥梁抗震设计规范》,同《AASHTO LFRD桥梁抗震设计细则》[2]等国外标准类似,对桥梁抗震设计的要求提高。21世纪以来,学者对既有桥梁网络地震风险的决策评估有持续的研究,M.LIU等[3]提出了一个基于概率的综合数学模型,用于评估桥梁网络关键节点连通性和桥梁抗震性能的概率分析;Y.C.YUE等[4]对HAZUS系统[5]进行了二次开发,建立了意大利特伦蒂诺省的桥梁网络地震风险的健康曲线;M.M.MESSORE等[6]针对既有桥梁网络地震风险,提出了一个基于全生命周期成本的概率框架,用以评估不同空间分布的在役桥梁的地震风险,研究中地震风险根据基于成本目标阈值的年度超越概率制定;J.WANG等[7]使用改进的Order-Ⅱ-Dijkstra算法,为大型的国家级公路桥梁网络建立了一个贝叶斯网络地震风险评估系统;邢云斐[8]制定了一个城市桥梁抗震性能评估方法,针对合肥地区城市桥梁的地震危险性级别做出了研究;刘振亮等[9]考虑灾后救援决策,基于图论和结构易损性分析提出了一个桥梁网络的抗震加固优先级决策方法;董优等[10]基于抗震韧性理论给出了城市桥梁网络抗震脆弱程度的分析方法。

综上,既有桥梁网络的地震风险评估与分级是近年桥梁工程及防灾工程领域的一个热点,但现有的研究中存在缺陷,包括桥梁网络中社会属性重要程度在综合评估体系中的体现不够明确,过于依赖于经验判断以及桥梁结构易损性分析改进优化等问题。笔者提出一个多尺度的既有桥梁网络地震风险综合评估方法,并改进桥梁结构抗震性能分析手段,最后基于CRITIC-熵的客观赋权法解决不同的评估标准的加权统一的问题。

1 多尺度评估桥梁网络地震风险

单一桥梁节点或路段在区域桥梁网络中的地震风险评估需要考虑的重要性因素至少包括3个方面:①桥梁在社会属性层面上的重要程度;②桥梁节点在桥梁网络中几何属性的重要程度;③桥梁结构自身的抗震性能的强弱程度。桥梁几何属性重要度可以根据基于图论的网络模型和路段拓扑特性来表征,桥梁结构的抗震性能则通常使用易损性分析结果来表征,而桥梁社会属性重要度与前两者相比更抽象、难以量化。有鉴于此,笔者提出多尺度的桥梁网络地震风险评估,将定性描述的桥梁社会属性重要度作为第一尺度,将桥梁拓扑重要度和易损性分析作为第二尺度。

在地震风险评估的第一尺度中,采用定性的方法,提出评估区域内的特殊路段并将路段上的关键桥梁定义为特定等级的地震风险以及抗震加固优先级。特殊路段定义为:经过党政军部门、能源化工、医院、学校等重要部门及重要基础设施的主要道路。第一尺度具体的定性划分原则参考表1,实际工程评估可根据对象的特定情况做出相应调整。经过第一尺度的地震风险评估,可以得到桥梁网络中不同社会属性等级的桥梁分类,对于同等级桥梁则需要进行第二尺度的地震风险分析,进一步获取目标区域桥梁网络的地震风险等级、抗震加固的优先顺序。

表1 地震风险综合评估方法第一尺度重要度划分原则Table 1 Principles for the first scale importance classification of comprehensive seismic hazard assessment method

第二尺度的风险分析包括基于图论得到的拓扑特性以及基于易损性分析得到的结构抗震性能2个部分。由于是不同的量纲,因此选择合适的客观赋权法将两个因素加权统一。

笔者提出的多尺度分析方法步骤如图1。

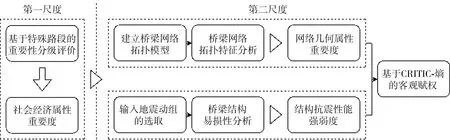
图1 多尺度评估桥梁网络地震风险流程Fig. 1 Flow chart of multi-scale assessment of bridge network’s seismic hazard

2 抗震性能分析及拓扑特征选取

2.1 既有桥梁抗震重要性系数衰减

对于既有桥梁结构抗震性能的评估,需要考虑既有桥梁的抗震设防标准。在桥梁网络抗震风险评估与分级研究中,因为已服役一定年限的桥梁拥有更短的剩余使用寿命,其地震风险评估所使用的抗震设防标准应低于新建桥梁的标准。根据风险一致性原则,可以推导出不同剩余使用寿命的桥梁衰减过后的抗震重要性系数[11]。

根据重要性系数C及基本烈度Ie计算出对应的极值Ⅲ型概率分布pⅢ,a,如式(1):

(1)

式中:ω为最大地震烈度;ε为基本烈度值减去1.55。

根据极值Ⅲ型概率分布计算出设计基准期内的超越概率p,如式(2):

(2)

式中:tL为设计基准期。

根据风险一致性原则,将式(2)计算得到的p用作一定剩余使用寿命t内的超越概率计算,最终得到衰减后的抗震重要性系数Cr,如式(3):

Cr=10(Ib-Ie)·log102

(3)

式中:Ib为对应的地震烈度,Ib=ω-(ω-ε)·[-ln(1-pⅢ,b)]1/k;υb、pⅢ,b分别为在剩余使用寿命t下,超越概率为p所对应的年超越概率及极值Ⅲ型概率分布,νb=1-(1-p)1/t,pⅢ,b=1-(1-νb)50。

2.2 改进的易损性分析输入地震动选取

通过目标结构有限元模型的大量的非线性动力时程分析,并选取特定的结构破坏状态限值,计算结构的地震响应超出限值的条件概率,可以评估地震风险。

多自由度体系非线性结构的动力分析具有极高的不可预测性,包括刚度的本构模型、阻尼模型等结构参数的不确定性,设计地震动选取的不确定性及不同的微分方程组,计算求解方法带来的结果不确定性。对于现有的桥梁结构易损性分析输入地震动的选取,主要存在2个问题:①选取输入地震波组过程中鲜有考虑多样性程度,只有输入能够激励目标模型不同动力响应特性的地震波组,才能降低易损性分析过程的不确定性;②需要大量的输入地震波,极大提升了设计和研究成本。

地震动强度指标可用来直观判断地震波可能激励结构的响应大小,如峰值加速度或结构特征周期对应的谱加速度等,但强度指标很难反映目标结构的非线性动力特性。因此,考虑简化目标结构,利用具有相似非线性动力特性的简化模型的损伤指标来体现输入地震动的特性。R.HONDA等[12]提出一个以三折线本构的10自由度框架体系,模拟了10层的钢筋混凝土框架结构,并选取了Park-Ang损伤指标评估地震动特性,但该简化模型动力学参数的规定方法并没有给出,通过10阶模态参数推导10自由度弹簧体系的刚度取值也十分困难。笔者根据规则梁桥顺桥向的动力特性,建立一个二折线非弹性本构的二自由度弹簧体系[13],通过求解模态方程得到非弹性本构的参数,模拟出目标桥梁结构在顺桥向的动力特性,该模型示意如图2。

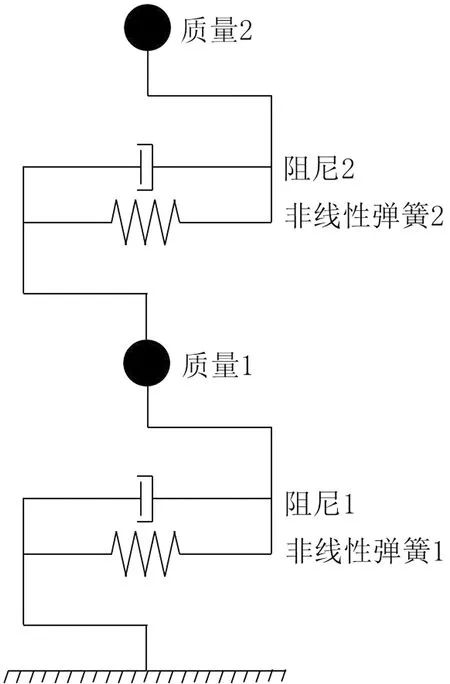
图2 二自由度简化模型示意Fig. 2 Sketch of the simplified two-degree-of-freedom model

假设质量1与质量2均取m,可以建立关于2个非线性弹簧的初始刚度k1及k2关于顺桥向前2阶频率ω1和ω2的模态方程:

(4)

求解式(4),可得:

(5)

根据式(5),通过目标桥梁结构的有限元模型模态分析,得到顺桥向前2阶振型频率,即可求解简化模型的非线性弹簧初始刚度。而基于减隔震梁式桥的动力特性,一般认为减隔震梁式桥顺桥向的前两阶振型为主梁振动以及下部结构振动,因此在目标结构为一般减隔震梁式桥的情况下,笔者提出的二自由度简化模型的参数,可直接根据桥梁设计参数计算得到。

对简化模型进行动力时程分析,将质量2的最大响应位移作为损伤指标,可在较短时间内计算出作为地震波组中每条地震波所对应的强度指标。针对特定地震波组对应的离散数据,将极值间等比例划分区间,从而得到损伤指标的概率密度函数(PDF),使用信息熵作为工具以衡量PDF中多样性的尺度。

作为信息论中,量化度量信源不确定度的常用工具,通过使用信息熵对输入地震波组的PDF进行评估,选取信息熵最高的候选地震波组作为目标桥梁结构的易损性分析输入地震波组,使输入地震波激励下的目标结构的响应尽量发散,以概括实际可能发生的全部地震响应状况,算法如式(6):

(6)

式中:H(P)为概率密度函数P对应的信息熵;pn为PDF中第n个损伤指标区间的概率。

2.3 桥梁网络拓扑特征选取

城市交通网络是典型的复杂网络,忽略网络中节点的大小、位置、形状、功能及节点间作用关系后,可抽象为由点和线组成的空间几何图形,称为网络拓扑结构图。选取桥梁网络拓扑结构图中待评估关键节点或边的度中心性、接近中心性、中介中心性作为评价指标,3项指标均衡量节点及边的网络局部特性,既为独立指标又互相关联。基于这个特点,利用灰色关联度理论[14]描述3项指标间的相对变换和关联性,作为评估桥梁的拓扑特性的综合评价指标。方法如下:

根据图论中的定义,求出拓扑网络中待评价的关键节点或边的度中心性、接近中心性、中介中心性3项指标。确定节点的比较数列以及参考数列:

Y(j)={Xi(j)}max

(7)

式中:Xi(j)为第i个节点对应的第j个评价指标;Y(j)为第j个评价指标在所有节点中的最优值。

采用均值法对3项指标进行无量纲化处理,再求出无量纲化后,比较数列与参考数列差值绝对值的最大值和最小值:

(8)

式中:Pi(j)为无量纲化后比较数列与参考数列差值。

令Pi(j)最大值为Δmax,最小值为Δmin。进一步计算出关联系数ξi(j):

(9)

式中:ρ为分辨系数,笔者研究中取0.5。

最后,将每个目标节点的3项指标对应的关联系数求和,即得到路网中每座桥梁的关联度γi:

(10)

3 基于CRITIC-熵权法的地震风险综合评价

针对组合测算模型,熵权法及CRITIC法均为目前学术界常用的客观赋权方法,其中CRITIC法可兼顾考虑各指标间的对比强度和冲突性,并由此综合确定指标的客观权数。然而单一的CRITIC法未能虑及指标间的离散性,熵权法则可有效弥补这一不足[15]。笔者使用CRITIC-熵权法客观赋权,综合评价桥梁网络中关键节点基于拓扑特性以及结构抗震性能的地震风险分级。

对熵权法以及CRITIC法2项指标标准化之后,使用CRITIC法计算客观权重Rn:

(11)

(12)

(13)

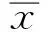
使用熵权法计算客观权重En:

(14)

(15)

(16)

式中,η′i,n为第i座桥的第n个评价指标;η′n为第n个指标序列;ηi,n为η′i,n对应的临界标准化值;en为第n个评价评价指标的信息熵。

Rn与En的算数平均就是桥梁网络地震风险评估指标的综合权重。

4 算 例

选取某市主要城区的道路桥梁网络作为研究对象,对14座跨江桥梁进行地震风险多尺度评估分析,形成了桥梁道路网络拓扑特征提取以及综合赋权法地震风险评估的算例。图3为选定区域主要道路的平面网络模型,空心圆圈代表主要道路上的交叉节点,实心圆圈代表14座需要地震风险评估和分级的关键节点桥梁。

基于多尺度的风险评估方法,第一尺度中以特殊路段的标准将14座桥梁分为3组,第1组包含2座桥梁(6号、11号),依据为该路段通过市政府;第2组包含3座桥梁(4号、9号、10号),依据为相应路段有通过次级的重要基础设施;剩下的9座桥梁为一组,具有相对最低的优先级。

计算出道路网络中重要桥梁所在的边的度中心性、接近中心性、中介中心性,并对14座桥梁做抗震易损性分析,易损性分析中输入地震波的选择遵循了2.1节中基于桥梁服役剩余寿命的重要性系数衰减,以及2.2节中考虑了相对较高信息熵的输入地震波组。选取抗震易损性分析中8度对应的地震动峰值加速度(PGA)对应的中等损伤超越概率,根据CJJ 166—2011《城市桥梁抗震设计规范》有:

A=C·a

(17)

式中:a为设防烈度的加速度,8度对应取0.3g;C为抗震重要性系数,根据《城市桥梁抗震设计规范》中0.3g抗震设防分类对应取值1.7,并根据每座桥梁的剩余使用寿命对抗震重要性系数按式(3)进行折减;A为易损性分析所取的时程峰值加速度,按式(17)计算得到为0.51g。

相应累计对数概率密度分布的易损性曲线如图4,拓扑特性及损伤概率计算结果如表2。

表2 桥梁中等破坏易损性概率及拓扑特性Table 2 Vulnerability probability and topological characteristics of moderate damage in bridges

将表2中的数据代入式(12)～式(14),得到地震易损性和拓扑特性对应的CRITIC权重R1、R2分别为0.380、0.620;将数据代入式(15)～式(17),得到易损性和拓扑特性对应的熵权法权重E1、E2分别为0.420、0.580。计算2种权重的算数平均值,得到综合权重S1、S2分别取0.400、0.600。将表2数据归一化后再代入综合权重则能计算出14座桥梁的综合地震风险,结果见表3。

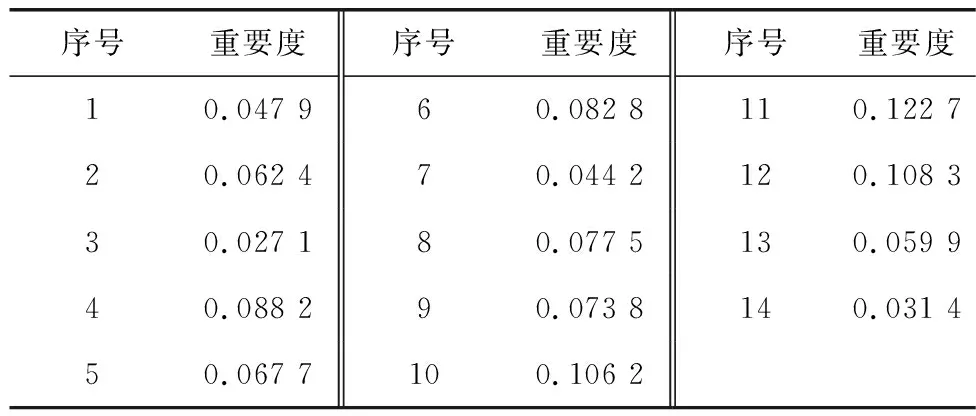
表3 14座桥梁抗震风险重要度Table 3 Importance of anti-seismic hazard for 14 bridges

将表3中的计算结果结合第一尺度的评估结果,即可得到14座桥梁的抗震风险等级,由高到低排列为:11号>6号>10号>4号>9号>8号>12号>5号>2号>13号>1号>7号>14号>3号。可作为城市桥梁网络抗震加固优先级的决策依据。

5 结 论

1)针对城市道路网络中桥梁地震风险评估的问题提出了一个多尺度的评估方法,考虑了既有桥梁抗震设防标准的修正,并改进了传统的地震易损性分析,对输入地震波组的选择提出了以信息熵恒量地震波组多样性的方法;提出了一个基于灰色关联度理论的桥梁网络拓扑特性的计算方法;综合考虑了桥梁的结构抗震性能、拓扑特性以及对于城市社会属性的影响,多尺度地将桥梁的地震风险进行分级,并基于CRITIC-熵权法客观赋权计算出桥梁的综合重要度。

2)从算例中可以看到,笔者方法实现了决策过程的量化,可以作为评估道路网络中桥梁地震风险、判断城市桥梁抗震加固优先级的可靠的依据。