云边端环境下可验证的轻量化可搜索加密

杜瑞忠　蒋浩宇　李明月

摘要： 传统公钥可搜索加密方案中，大多采用分布式双陷门公钥密码系统分发密钥，通过子集决策机制实现密文检索，但是系统之间通信开销较大。本文提出了1种新的可验证的云边端环境下的公钥可搜索加密方案VSE－EPOMFC（Verifiable Searchable Encryption- Efficient Privacy－preserving Outsourced calculation framework with Multiple keys Filtering Computing， VSE－EPOMFC）。方案VSE－EPOMFC设计了1种基于部分同态加密的能在密文下计算的过滤算法筛选无意义任务来降低通信开销。针对客户端设备资源受限的缺点，采用阈值签名机制，将客户端签名、验证的任务委托给边缘结点，轻量化了客户端的验证开销与存储开销。仿真实验结果表明，方案VSE－EPOMFC在任务集匹配度II的情况下通信时间节省了25.46%，在任务集匹配度I的情况下通信时间节省了62.21%。

关键词：公钥可搜索加密；可验证；轻量化；云边端

中图分类号：中图分类号TP309.7文献标志码：A文献标识码

Verifiable lightweight searchable encryption in cloud edge environment

DU  Ruizhong1，2，JIANG  Haoyu1，2，LI  Mingyue1，2

（1 School of Cyber Security and Computer， Hebei University， Baoding，Hebei 071002， China; 2 Hebei Key Laboratory

of Highly Trusted Information System， Baoding，Hebei 071002， China）

Abstract：  In the traditional public key searchable encryption schemes， the distributed two－trapdoor public key cryptosystem is mostly used to distribute the key， and the ciphertext retrieval is realized through the subset decision mechanism， but the communication overhead between systems is relatively large. This paper proposes a new verifiable public key searchable encryption scheme on cloud－edge －end environment （Verifiable Searchable Encryption Efficient Privacy－preserving Outsourced calculation framework with Multiple keys Filtering Computing， VSE－EPOMFC）. Scheme VSE－EPOMFC designs a filtering algorithm based on partial homomorphic encryption that can be calculated under ciphertext to filter meaningless tasks to reduce communication overhead. In view of the limitation of client device resources， the threshold signature mechanism is used to entrust the task of client signature and verification to the edge node， which lightens the verification and storage overhead of the client. The simulation results show that the communication time of VSE－EPOMFC is saved by 25.46% in the case of task set matching degree II and 62.21% in the case of task set matching degree I.

Key words： PEKS;verifiable;lightweight;cloud－edge－end environment

近些年，隨着物联网和大数据的迅速发展，据GSMA预测，2025年全球物联网终端连接数量将达到250亿，物联网设备数量将爆发式增长① https：//m.thepaper.cn/baijiahao_17826588。由于物联网设备计算能力较弱，只能处理轻量级的任务，并且需要将复杂任务外包，因此逐渐形成了云边端模型。在云边端模型中，各方实体都是半可信的，边缘节点能够在数据所有者不知道的情况下窃取他们的信息并执行恶意操作。为了保护数据隐私，数据持有人需要在敏感数据外包之前对其加密。一种方法是用户可以下载全部数据并解密，但是这种方法下载了大量不必要的数据，显然不具备可用性［2］。

为了解决上述问题，提出了云边端环境下的可搜索加密方案，轻量化客户端的存储与计算开销，解决了客户端设备资源受限的问题。另一方面，由于半可信的云端可能返回不正确的搜索结果，设计基于可验证的可搜索加密方案是近年来的另一个目标。

本文提出了可验证的轻量化VSE－EPOMFC方案，设计了1种过滤算法来降低系统开销。贡献主要体现在以下3个方面：

（1） 引入了边缘结点代替客户端执行计算签名及验证的任务，轻量化了客户端验证与存储开销。边缘结点解决了客户端计算、存储资源匮乏的问题。

（2） 利用分布式双陷門公钥密码系统 （Distributed Two－Trapdoor Public－Key Cryptosystem，DT－PKC）、子集决策机制、部分同态加密3种技术，本研究设计了1种搜索前过滤搜索任务的算法，整个过程在密文下计算，保障用户隐私，能在任务集有较多的无意义任务的情况下，减少系统的通信开销。

（3） 仿真实验评估了方案VSE－EPOMFC与SE－EPOM在搜索时的通信开销，与方案CP－ABKS比较了客户端的验证开销。实验结果表明方案VSE－EPOMFC在搜索性能与验证性能方面都有一定程度的提升。

对称可搜索加密（Symmetric Searchable Encryption， SSE）计算速度快，但是存在严重的密钥管理问题。为了解决以上问题，Boneh等［3］首先提出了基于公钥的可搜索加密方案（Public Key Encryption with Keyword Search，PEKS），减少了多用户场景下的密钥数量。为了保证搜索结果的正确性，Zhang等［4］提出了1种可验证的无证书的公钥可搜索加密方案，解决了密钥托管和证书管理问题。Liu等［5］设计了1种在多用户环境下的可验证的动态SSE方案，云服务器使用RSA累加器返回验证信息给用户。文献［4-5］方案需要用户或者数据持有人执行一定的验证操作，对于多用户下资源受限的客户端设备是1个挑战。Chen等［6］在车载社交网络的背景下，使用智能合约代替云服务器进行搜索和验证，降低了客户端的验证开销。从安全角度出发，Du等［7］通过引入区块链实现了数据持有人与用户之间的双向认证，同时满足前向和后向安全。Song等［8］通过利用重加密密码系统和索引洗牌协议保护搜索模式和访问模式。为了降低客户端的压力，Wang等［9］提出了1种基于工业物联网环境下的轻量级PEKS方案，将复杂的任务委托给边缘结点，消除了大部分方案由于双线性配对运算带来的沉重的计算开销。He等［10］提出了1种新颖的鱼骨链结构，保证了客户端的存储开销与关键字数量无关。

PEKS面临KGA（Keyword Guess Attack）这一固有问题，主要原因是关键字空间远远小于密文空间，在实际搜索过程中，恶意用户通常会选择一些使用频率较高的热词进行搜索。Chen等［11］提出了1种新的服务器辅助的PEKS方案SA－PEKS。使用辅助的服务器作为中介，数据持有人和用户在生成可搜索密文和搜索陷门之前必须向关键字服务器（Keyword Server，KS）验证身份并运行交互协议才能返回二次处理的可搜索密文、陷门。通过这种方法，将可搜索密文、陷门的生成过程变成了1种在线的方式，从而防止了恶意的内部服务器的攻击。Chen等［12］紧接着提出了1种双服务器测试的DS－PEKS方案，与前者设计思路类似，使用前端服务器预处理并发送状态信息、密文，后端服务器产生最终的陷门、可搜索密文并测试。2019年，Hwang等［13］提出了基于ElGamal密码系统的无通道安全PEKS方案，同时防止了内部、外部的攻击。文献［14］中，利用2个非共谋的服务器抵抗内部KGA，免双线性对运算的结构轻量化了客户端的开销。

Huang等［15］构建了1个具有多关键字搜索的PEKS方案PE－MKS，但是没有支持恒定大小的搜索陷门、可搜索密文，它们的大小与关键字数量呈线性关系。Wu等［16］提出了1种多用户环境下基于同态加密的可验证的PEKS方案。对于现有的公钥可搜索加密方案，构建主要依赖于双线性配对。但是，PEKS在客户端的计算较为复杂［17］。因此，常见的设计轻量级PEKS方案的思路就是用某些操作替换昂贵的双线性配对。我们还可以像Liu等［18］提出的方案一样，设计1种在线、离线加密，将完整的过程划分成2部分，离线部分可以预先计算，从而减少了复杂的客户端加密开销。2020年，Liu等［19］提出了在分布式系统中执行搜索的多关键字PEKS方案，攻击者想要执行KGA需要获取多个服务器的密钥，因此方案SE－EPOM成功抵抗了来自内部、外部攻击者的攻击。但是该方案在半可信云服务器环境下构建，缺乏对搜索结果的验证。此外，还存在系统之间通信开销过大的问题。Zhang等［20］提出了1种双向的公钥可搜索加密方案。文献［21-22］构建了基于密文策略的可搜索加密方案，提供了细粒度的访问控制，在文献［23］中，客户端需要计算额外的验证过程，对于资源受限的设备是1个很大的挑战。针对以上问题，本文提出了云边端环境下可验证的轻量化可搜索加密方案。

1 资料与方法

1.1 预备知识

1.1.1 DT－PKC

分布式双陷门公钥密码系统（DT－PKC）可以将1个强私钥SK=λ分成2部分，使得方案不仅支持弱私钥ski解密，还可以通过分解强私钥SKi=λi进行分布式解密，本文工作主要用到以下算法［24］：

1.2 模型构建

1.2.1 系统模型

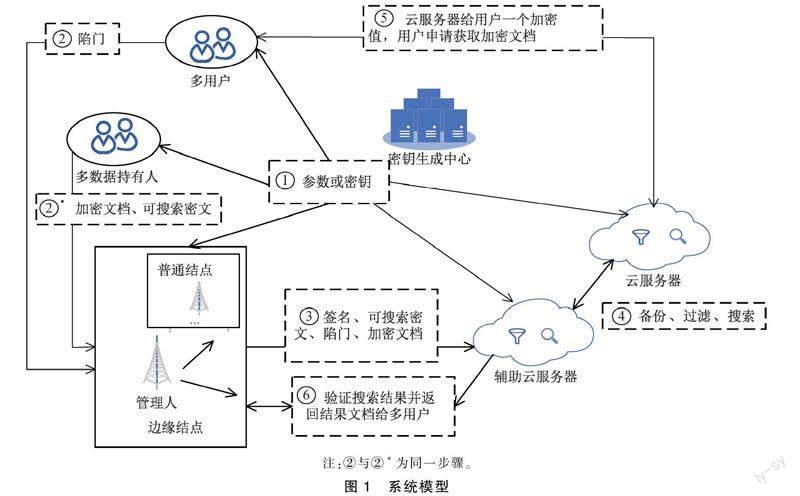
在方案VSE－EPOMFC中，系统由6部分实体组成，包括密钥生成中心KGC（Key Generate Center， KGC）、多数据持有人MDO（Multi Data Owners， MDO）、边缘结点EN（Edge Node， EN）、多用户MDU（Multi Data Users， MDU）、云服务器CP（Cloud Platform， CP）和提供辅助计算服务的CSP（Cloud Service Provider， CSP）。图1描述了系统模型，例如，企业将敏感数据外包给云服务器CP，方便授权的公司员工能够随时随地访问这些数据。在外包存储到云服务器之前，应当选择一部分结点作为管理人ENM （Edge Node Manger， ENM），为上传的密文数据签名，避免了以往方案中必须全部数据持有人同时在线签名的限制。

（1）密钥生成中心KGC负责产生并分发公共参数给多用户MDU和多数据持有人MDO，分发部强私钥给CP和CSP（实际生活中可以由政府等公信力强的机构担任），为边缘结点管理人ENM产生密钥对。

（2）多用户MDU和多数据持有人MDO依靠从KGC产生的公共参数产生属于自己的密钥对，使用各自的公鑰产生可搜索密文SC和陷门TD，使用对称密钥加密文件，分别将加密文档、可搜索密文和搜索陷门上传至边缘结点。

（3）边缘结点主要由两部分组成：代理边缘结点ENM和普通边缘结点EN。签名由EN和ENM完成，ENM将多个边缘结点产生的签名进行整合，缩短了签名长度。边缘结点将加密文档、可搜索密文和搜索陷门以及签名上传至CP。

（4）CP将加密文档、可搜索密文、搜索陷门以及签名在CSP备份。CP和CSP交互式的执行子集决策机制、跨域安全计算协议，完成过滤和搜索，计算一个加密值。

（5）CP将加密值交给MDU。由MDU判断对应的加密文档是否属于最终的搜索结果。MDU向CP申请获取满足条件的加密文档。

（6）CSP收到MDU获取加密文档的请求之后，通过与ENM交互对相关加密文档进行结果验证，删除其中被半可信云服务器增加的恶意文档。CSP返回经过搜索和验证的加密文档给MDU，MDU通过以上步骤获取与感兴趣关键字相关结果文档。

1.2.2 威胁模型

在方案VSE－EPOMFC中，密钥生成中心KGC被假设为是完全可信的，诚实的遵循协议去产生公共参数或者分发密钥到各个实体。CP和CSP以及EN被假设为半可信的，即会诚实的遵循协议完成工作，但是会尝试从加密的信息中推断敏感信息。CP和CSP在过滤和搜索2个阶段被假设为非共谋的2个实体。

多用户MDU和多数据持有人MDO同样是半可信的实体，会诚实的遵循协议完成工作。但是MDO可能会窃听其他实体之间的通信，或者尝试了解陷门信息。MDU可能会尝试了解可搜索密文的信息或者由其他MDU上传的陷门信息。

1.2.3 安全性定义

安全多方计算的安全定义

Kamara等［26］表示处在多方协议计算之间的共谋攻击是1种有用信息的交换。这种有用信息指的是可信实体在整个协议计算过程中未规定过的输入信息。只要多方参与者（敌手）能了解到这部分信息，那么共谋攻击成立。方案SE－EPOMFC假设处在非共谋敌手攻击模型下。

安全多方计算的安全性通过1种理想/现实世界模型来定义的。在当前模型中，必须首先设置集合P=（PMDO，PMDU，PCSP，PCP）表示各方执行协议的实体对象，各方实体之间只能交互非协议信息。这里的各方实体主要包含4部分，包括MDO，MDU，还有负责过滤和搜索的CP和CSP。相应的会有敌手A=（AMDO，AMDU，ACSP，ACP）负责攻击各个实体。

在现实世界中，执行各种协议发生在各个实体P=（PMDO，PMDU，PCSP，PCP）之间，我们让H∈P表示实体中完全可信的实体集合，让J∈P-H表示实体中受到非共谋敌手攻击并被破坏的实体集合。

再执行过程的初始阶段，P=（PMDO，PMDU，PCSP，PCP）中的实体PMDO或PMDU会收到输入xMDO和xi，以及辅助输入ZMDO和Zi，CP和CSP仅仅收到辅助输入ZCP和ZCSP。当P是可信实体时，P∈H，outp是实体Pi的输出。当P属于被破坏的实体时，P∈I，outp输出产生的是P执行协议之后产生的新的输出（被破坏的实体可能产生攻击者伪造的输出）。

某一部分实体Pi在现实世界中多方实体P=（PMDO，PMDU，PCSP，PCP）之间，同时存在敌手A=（AMDO，AMDU，ACSP，ACP）的情况下，执行协议Π所产生的结果定义为：

IDEALPiΠ，，，z（k，x）={outp：P∈I}∪outpi。（1）

在理想世界中，所有的实体都会与完全可信的评估实体交互，在模拟器S=（SMDO，SMDU，SCSP，SCP）存在的情况下产生评估实体，我们用表示完全可信的评估实体。挑战者会发送xi给。如果xi是⊥，那么返回⊥。否则，返回（x1，…，xi）给挑战者。当P是可信实体时，P∈H，outp是完全可信实体返回给实体Pi的输出。当P是属于被破坏的实

密文不可区分性指的是上传到CP和CSP的加密的可搜索密文不会泄露隐藏的关键字信息。同理，陷门隐私与密文不可区分性具有相似的概念，指的是产生的搜索陷门不会泄露隐藏的关键字信息。不可区分性游戏模型可以这样定义：敌手选择2个不同的关键字集发送给挑战者，挑战者随机选择一个计算可搜索密文并返回给敌手，此时，敌手尝试猜测哪一个关键字集与挑战者返回的密文对应。

假如不存在敌手A能在概率多项式时间内从可搜索密文和搜索陷门中推断出敏感的关键字信息，则关键字隐私能够得到保障。定义的安全隐私游戏如下：

（1）初始化。通过输入指定的k，挑战者运行KeyGen算法产生SKCP，SKCSP，PKMDO，PKMDU，SKMDO，将SKCP，PKMDO，PKMDU发送给敌手A，私钥SKCSP，SKMDO自己保留。

（2）挑战。 敌手A选择了两对不同的关键字集合W0和W1，发送给挑战者C。挑战者从r∈0，1中随机选择一个值，运行算法Searchcp产生可搜索密文SC，发送给敌手A。

（1）初始化。通过输入指定的k，挑战者运行KeyGen算法产生SKCP，SKCSP，PKMDO，PKMDU，SKMDO，将SKCP，PKMDO，PKMDU发送给敌手A，私钥SKCSP，SKMDO自己保留。

1.3 VSE－EPOMFC

本节从验证轻量化、任务过滤2个小节简单介绍了创新之处，首先将客户端签名和验证的任务委托给边缘结点降低客户端的计算和存储开销，然后在搜索之前对任务进行过滤，筛选一部分不匹配的任务，降低系统之间的通信开销。最后，具体方案构造描述了算法细节。在表1中定义了论文使用的符号。

1.3.1 验证轻量化

SE－EPOM通过引入通用关键字集W，将多关键字用二进制串形式加密，保证可搜索密文和陷门的大小与关键字数量无关。但是考虑到恶意的多数据持有人MDO、云服务器CP、CSP可能上传错误的密文或者返回错误的搜索结果，通常是由MDO对密文进行签名，MDU负责对搜索结果验签，此时客户端将承担计算密文、签名、验证签名的任务，对于资源受限的客户端设备，显然是不可取的。因此，引入了边缘结点代替MDO对密文执行签名，代替MDU验证签名，轻量化客户端的验证开销。使用1种阈值签名机制，先由边缘结点EN1，EN2，…，ENi代替阈值数量的MDO对密文分别签名，设置1个管理人ENM，根据多个签名为每个文档生成唯一的阈值签名，缩短了签名长度。

1.3.2 任务过滤

由于实际搜索过程中，需要用到大量的交互式算法，通信较为复杂，为了解决通信过程中由于大量不匹配的任务产生的不必要的通信开销的问题，在子集决策机制的基础上设计了1个过滤算法用于过滤完全不匹配的任务。

方案在搜索过程中用到了SE－EPOM中的子集决策机制，在密文的基础上使用CP和CSP进行搜索。但是，当任务集中存在大量完全不匹配的加密二进制串时，方案SE－EPOM会产生多余的通信开销。VSE－EPOMFC在搜索过程中增加了1个过滤算法，负责筛选完全不匹配的二进制串，如图2所示。

只有当2个二进制串完全不匹配时，过滤算法生效。对密文进行计算，只能使用安全位加法和安全位乘法运算。为了便于理解，本文使用明文下的例子进行说明，实际情况下则需要在加密的二进制串上运行各种复杂的通信协议。过滤算法用于判断两个二进制串是否完全不匹配。首先当每个对应的加密位都不相同时，运用安全位乘法协议必定产生全为0的加密二进制串，接着使用安全位加法协议，对所有位累加，最后将结果交给多用户MDU解密，如果结果为零表示2个二进制串必定完全不匹配，将其从任务集中删除。

1.3.3 具体方案构造

（1）初始化。 （SK，SK1，SK2，PP，H0，H1）←Setup（k）。

KGC首先执行KeyGen得到强私钥SK=λ，N=pq，s=-a2N（其中a∈Z*N2是随机选取的）。然后KGC执行SKeys对强私钥λ进行拆分，得到2个部分强私钥SK1=λ1，SK2=λ2。G和GT是2个大素数p阶循环群，g是循环群G的生成元，e：G×G→GT是1个双线性映射，选择双线性对参数BP={G，GT，e，p，g}，选择2个抗碰撞哈希函数，H0：{0，1}*→Zp，H1：{0，1}*→G。最后，KGC将产生的参数PP={N，s，BP}，发送给多用户MDU和多数据持有人MDO。将部分强私钥SK1=λ1，SK2=λ2分发给CP和CSP，强私钥λ秘密保存。

（2）生成密钥。（pkMDU，skMDU，pkMDO，skMDO，pkm，skm）←KeyGen（SK，SK1，SK2，PP，ENi，ENM）。

MDU和MDO拿到公共参数PP=（N，s，BP）后执行KeyGen产生属于自己的密钥对pkMDU，skMDU，pkMDO，skMDO。将ENM管理的边缘结点小组设为EN=EN1，EN2，…，ENi，KGC会为ENM产生密钥对（pkm=gb，skm=b），b∈Zp，管理人会输出1个ξ-1次的多项式f（x）=cξ-1xξ-1+…+c1x+c0，这里cj∈Zp（j∈［1，ξ-1］），c0=b，i≤2ξ-1。管理人选择i个满足多项式的元素对{（x1，y1），（x2，y2），…，（xi，yi）}，y1，…，yi 值发送给剩余边缘结点EN1，EN2，…，ENi用于签名。

（3）加密并签名。（Cm，SCm，τ）←Searchcp（Did，W，WT，pkMDO，pkm）。

执行表2算法1，分别使用AES和DT－PKC计算加密文档和可搜索密文，然后计算至少阈值数量的签名，管理人ENM将全部的签名整合成唯一阈值签名，从而缩短了签名长度。

如表3算法2所示，最后得到了2个所有位都被加密的二进制串SC′m，TD′m。在这2组子串中，使用SMD协议相乘得到ftimpkMDU，使用SAD协议对ftimpkMDU中的每一位进行累加，结果记为ftmpkMDU，交给用户使用弱私鑰skMDU解密得到fmt，若fmt=0，则用户返回“需要过滤”，否则返回“不需要过滤”。

执行搜索需要获取公钥pkMDU，pkMDO，CP和CSP提供部分强私钥SK1，SK2以及经过过滤的可搜索密文SC′m和陷门TD′m，CP和CSP执行表4算法3，用户最终获得fmpkMDU后使用弱私钥skMDU解密。若结果输出0，表示陷门与可搜索密文不匹配；若结果输出1，表示陷门与可搜索密文匹配，用户向CP申请获取相关的文档C*m。

2 结果与分析

2.1 安全性分析

本节是安全性证明，需要证明2个部分：首先，证明方案VSE－EPOMFC能被安全实现。然后证明如果方案能安全实现（各方之间的协议是安全的），那么方案满足密文不可区分性以及陷门隐私性。

定理1 方案VSE－EPOMFC在满足敌手A=（AMDO，AMDU，ACSP，ACP）存在的情况下能被安全的实现。

证明  SimMDO收到输入x，通过执行以下的算法模拟敌手AMDO：首先计算TpkMDO←Enc（T，pkMDO），将结果返回给AMDO。因为DP－PKC满足语义安全（在VI－A定理1有详细描述），所以敌手AMDO在现实世界和理想世界输出的结果是难以区分的。

SimCP通过执行以下算法模拟敌手ACP：首先随机的从（0，…，2n-1）中选择T^，t^，加密产生（T^pkMDO，t^pkMDU）←Enc（T^，t^，pkMDO，pkMDU），计算t^pkMDU，T^pkMDO，-T^pkMDO，2个加密二进制串中对应的位使用SMD协议相乘得到f^tipkMDU。使用SAD协议对f^tipkMDU中的每一位进行累加，结果记为f^tpkMDU。SMD和SAD的安全性在VI－C定理2中有详细证明。

SimMDO与SimCP交互后确定过滤的任务，接下来使用与VI－C定理3证明过程相同的方法计算搜索过程中用到的加密中间值c^ipkMDU，d^ipkMDU，R^ipkMDU，f^ipkMDU。最后SimCP发送全部的加密中间值给ACP，如果ACP返回⊥，那么SimCP同样返回⊥。因为DT－PKC是满足语义安全的，MDO是诚实的，敌手ACP在现实世界和理想世界输出的结果是难以区分的。

SimCSP通过执行以下的算法模拟敌手ACSP：随机选择一些数字，使用与VI－C定理3证明过程相同的方法计算加密中间值。SimCSP发送全部的加密中间值给ACSP，如果ACSP返回⊥，那么SimCSP同样返回⊥。因为DT－PKC是满足语义安全的，MDO是诚实的，敌手ACP在理想世界和现实世界中输出的结果是难以区分的。

因此，方案VSE－EPOMFC能被安全实现得到证明。

定理2 如果方案VSE－EPOMFC能在满足敌手A=（AMDO，AMDU，ACSP，ACP）存在的情况下被安全的实现，那么该方案同时也满足密文不可区分性和陷门隐私。

证明 假设方案VSE－EPOMFC不满足密文不可区分性或者陷门隐私，那么该方案不能被安全的实现。

设置1个实体Z，它的目标是想方设法区分出现实世界和理想世界。

假设方案VSE－EPOMFC不满足定义1中的密文不可区分性，即存在一个敌手B使得等式（1）中的优势不可忽略。实体Z会要求A或者S破坏PCP，以便PCP将从PMDO收到的消息传输给Z。在整个过程中，PCP对外表现诚实可信，敌手B从Z内部执行攻击。如果B发送WT0，WT1∈W给挑战者C，那么：

（1） Z输入（Searchcp，sid，WT，b）给PMDO，b随机的从0，1中选择，sid表示文档id。

（2） 在现实世界中，PMDO计算SC并发送SC给PCP，PCP发送给实体Z。

（3） 在理想世界中，MDO发送（Searchcp，sid，WT，b）给f，f发送|WT，b|给S。S计算SC′发送给Z。

当且仅当B输出1时，Z输出1。输出1表示敌手B能区分出可搜索密文，即满足挑战者-敌手游戏。如果Z与协议∏交互，因为现实世界敌手A扮演ACP的角色，此时B模拟SC。如果Z与SCP交互，因为理想世界敌手S扮演SCP的角色，此时B模拟SC′。

根据我们的假设，存在1个敌手B，在现实世界中，它能以不可忽略的优势区分可搜索密文，输出1。而在理想世界中，输出1的概率为50%。显然，将B作为子程序运行的实体Z可以将现实世界中PCP执行的结果与理想世界中PCP执行的结果区分开来。协议∏不能安全地实现VSE－EPOMEC得到证明。

假设方案VSE－EPOMFC不满足定义2中的陷门不可区分性，即存在一个敌手B′使得等式（2）中的优势不可忽略。实体Z会要求A或者S破坏PCP，以便PCP将从PMDU收到的消息传输给Z。在整个过程中，PCP对外表现诚实可信，敌手B′从Z内部执行攻击。如果B′发送Wt0，Wt1∈W给挑战者，那么：

（1） Z输入（Trapdoor，sid，Wt，b）给PMDU，b随机的从0，1中选择，sid表示文档id。

（2） 在现实世界中，PMDU计算TD并发送TD给PCP，PCP发送给实体Z。

（3） 在理想世界中，MDU发送（Trapdoor，sid，Wt，b）给f，f发送|Wt，b|给S。S计算TD′发送给Z。

当且仅当B′输出1时，Z输出1。输出1表示敌手B′能区分出搜索陷门，即满足挑战者-敌手游戏。如果Z与协议∏交互，因为现实世界敌手A扮演ACP的角色，此时B′模拟TD。如果Z与SCP交互，因为理想世界敌手S扮演SCP的角色，此时B′模拟TD′。

根据我们的假设，存在1个敌手B′，在现实世界中，它能以不可忽略的优势区分搜索陷门，输出1。而在理想世界中，输出1的概率为50%。显然，将B′作为子程序运行的实体Z可以将现实世界中PCP执行的结果与理想世界中PCP执行的结果区分开来。证明协议∏不能安全地实现VSE－EPOMEC。综上，方案VSE－EPOMFC同时满足密文不可区分性和陷门隐私。

2.2 性能评估

2.2.1 理论评估

表5从性能和安全性2个方面出发，对不同方案实现的功能进行比较。其中MDU和MDO表示多用户、多数据持有人，LW表示轻量化，MK表示多关键字，IKGA和OKGA分别表示内部、外部关键字猜测攻击，CS表示可搜索密文大小，TS表示陷门大小，V表示搜索结果可验证。文献［3］是最早提出的公钥可搜索加密方案，支持单用户上传数据、多数据持有人查询，它的可搜索密文以及陷门大小必须随关键字数量|Wid|线性增长。在安全性方面，文献［13］基于1种密码系统，同时满足了IKGA与OKGA，文献［14］通过使用双服务器抵抗IKGA，设计了免双线性对的算法，轻量化了客户端的开销。文献［19］实现了大部分功能，但是客户端不具备验证搜索结果这一功能。文献［20］提出了1种支持双向关键字搜索的PEKS方案，允许数据持有人检索上传的数据。文献［23］支持轻量化和可验证性，但是其可搜索密文长度与属性数量|Ai|有关。方案VSE－EPOMFC讓边缘结点代替客户端实现签名并且验证搜索结果，轻量化了客户端的存储和计算开销。

2.2.2 实验评估

为了评估方案VSE－EPOMFC的实际性能，进行了实验。本实验使用python语言，通信过程使用socket编程建立TCP可靠连接。设置了2台虚拟机，将KGC，CP和MDO部署在具有6GB RAM和Intel（R） Core（TM） i5－10400F 2.90GHz处理器的Ubantu 20.04操作系统上，同时ENM（包括EN），CSP和MDU部署在具有4GB RAM和Intel（R） Core（TM） i5－10400F 2.90GHz处理器的Ubantu 20.04操作系统上。为了与方案SE－EPOM对比，实验设置80位安全级别，参数N选择1024位长。

實验主要选择了2种参数，一种是任务集完全不匹配任务所占的比例（搜索任务完全不匹配意味着对应的2个二进制串中所有的位均不匹配），我们用匹配度IV，III，II，I表示。当任务集完全不匹配的任务数为0时，匹配度为IV，表示不存在完全不匹配的任务。当任务集中有25%的任务完全不匹配，匹配度为III，以此类推。另一种参数选择关键字数量，分别为5、10、15、20。

图3比较了方案PEBKS，方案SE－EPOM以及VSE－EPOMFC方案在不同匹配度条件下，执行搜索的时间开销。PEBKS方案在单个服务器场景下执行搜索，所以搜索时间开销远远小于多台服务器环境下执行搜索的方案。SE－EPOM没有使用过滤算法，直接对任务集进行搜索，可以看出它的时间开销在11s上下波动，不受匹配度变化的影响。而方案VSE－EPOMFC由于使用了过滤算法，在匹配度为IV和III的条件下，过滤算法产生的时间开销更多，当匹配度在II以下时，过滤算法能显著降低SE－EPOM的时间开销。

图4和图5比较了方案LFGS，方案CP－ABKS，方案VSE－EPOMFC在客户端产生的验证时间开销与验证存储开销，方案VSE－EPOMFC将客户端执行签名和验证的任务委托给边缘结点，因此在客户端的开销与关键字数量无关。验证使用了阈值签名机制，边缘结点管理人ENM通过整合签名缩短了签名长度，也降低了验证的时间开销和存储开销。CP－ABKS同样支持搜索结果验证，但是需要用户执行部分解密和验证，给客户端的设备带来了额外开销。

LFGS方案能准确的验证搜索结果，但是它需要用户和数据持有人之间的交互，当返回大量搜索结果时，会产生更多通信开销。此外，LFGS方案只能支持单关键字搜索，不能部署在多关键字设置中执行搜索结果验证。LGFS方案使用的搜索结果验证机制主要依赖于本地存储的文件-关键字哈希表，如图6所示，当本地存储的文件-关键字哈希表较大时，会产生很高的计算开销，它的计算复杂度为O（|F||W|），而VSE－EPOMFC采用的搜索结果验证机制与文件数量有关，计算复杂度为O（|F|）。

过滤算法节省时间需要任务集一半以上的任务不完全匹配，更适用于特殊的场景，比如在某个医疗系统中，需要对病人的隐私实现高度的保密，医生只能了解其身体状况，其余信息一无所知，只能使用少量关键字去查询病人以获取病例信息。在当前场景下，病人作为数据持有人上传加密的病例信息、可搜索密文到云中心，医生作为用户，可以借助边缘设备签名并验证搜索结果的正确性。病人的隐私信息保密程度越高，医生搜索到完全不匹配任务的可能性越大，最终必定会产生大量不匹配任务。方案VSE－EPOMFC节省了医生与病人的时间，使其不用执行复杂的验证。

3 讨论与结论

本文设计了1个在云边端环境下可验证的轻量化可搜索加密方案，说明了其关于理想现实模型、关键字隐私模型的定义并给予证明。与先前的工作相比，轻量化客户端复杂的签名与验证开销。通过引入边缘结点，借助边缘结点的缓存，减少了主干网络上的流量负载。设计了1种过滤算法来降低搜索带来的通信开销。实验表明VSE－EPOMFC适用于任务集不完全匹配任务较多的情况。通过对比了几种方案在离线关键字猜测攻击、多关键字、多用户、多数据持有人、可验证性等方面的差异，表明了VSE－EPOMFC在整体的功能性、安全性、计算存储开销等方面具有一定的优势。未来工作考虑在当前方案基础上增加动态更新功能，同时对动态更新中关键字泄露问题做进一步研究。

参考文献（References）

［1］MAO Y， YOU C， ZHANG J， et al. A survey on mobile edge computing： the communication perspective［J］. IEEE Communications Surveys & Tutorials， 2017， 19（4）： 2322-2358.

［2］CUI M M， FEI Y M， LIU Y. A survey on secure deployment of mobile services in edge computing［J］. Security and Communication Networks， 2021（5）： 1-8.

［3］BONEH D， DI CRESCENZO G D， OSTROVSKY R， et al. Public key encryption with keyword search［C］//Advances in Cryptology－EUROCRYPT 2004： International Conference on the Theory and Applications of Cryptographic Techniques. Interlaken， Switzerland： Springer， 2004： 506-522.

［4］ZHANG L， JIANG F， TANG X. Verifiable conjunctive keyword search with certificateless searchable［C］//2021 IEEE 20th International Conference on Trust， Security and Privacy in Computing and Communications （TrustCom）. IEEE， 2021： 9-16.

［5］LIU X Q， YANG G M， MU Y， et al. Multi－user verifiable searchable symmetric encryption for cloud storage［J］. IEEE Transactions on Dependable and Secure Computing， 2020， 17（6）： 1322-1332.

［6］CHEN B， WU L， WANG H， et al. A blockchain－based searchable public－key encryption with forward and backward privacy for cloud－assisted vehicular social networks［J］. IEEE Transactions on Vehicular Technology， 2019， 69（6）： 5813-5825.

［7］DU R， WANG Y. Verifiable blockchain－based searchable encryption with forward and backward privacy［C］//2020 16th International Conference on Mobility， Sensing and Networking （MSN）. 2020： 630-635.

［8］SONG Q Y， LIU Z T， CAO J H， et al. SAP－SSE： Protecting search patterns and access patterns in searchable symmetric encryption［J］. IEEE Transactions on Information Forensics and Security， 2020， 16： 1795-1809.

［9］WANG W， XU P， LIU D L， et al. Lightweighted secure searching over public－key ciphertexts for edge－cloud－assisted industrial IoT devices［J］. IEEE Transactions on Industrial Informatics， 2020， 16（6）： 4221-4230.

［10］HE K， CHEN J， ZHOU Q X， et al. Secure dynamic searchable symmetric encryption with constant client storage cost［J］. IEEE Transactions on Information Forensics and Security， 2020， 16： 1538-1549.

［11］CHEN R M， MU Y， YANG G M， et al. Server－aided public key encryption with keyword search［J］. IEEE Transactions on Information Forensics and Security， 2016， 11（12）： 2833-2842.

［12］CHEN R M， MU Y， YANG G M， et al. Dual－server public－key encryption with keyword search for secure cloud storage［J］. IEEE Transactions on Information Forensics and Security， 2016， 11（4）： 789-798.

［13］HWANG M S， LEE C C， HSU S T. An ElGamal－like secure channel free public key encryption with keyword search scheme［J］. International Journal of Foundations of Computer Science， 2019， 30（2）： 255-273.

［14］CHEN B W， WU L B， ZEADALLY S， et al. Dual－server public－key authenticated encryption with keyword search［J］. IEEE Transactions on Cloud Computing， 2019， 10（1）： 322-333.

［15］HUANG K B， TSO R， CHEN Y C. Somewhat semantic secure public key encryption with filtered－equality－test in the standard model and its extension to searchable encryption［J］. Journal of Computer and System Sciences， 2017， 89： 400-409.

［16］WU D N， GAN Q Q， WANG X M. Verifiable public key encryption with keyword search based on homomorphic encryption in multi－user setting［J］. IEEE Access， 2018， 6： 42445-42453.

［17］SHAO J， CAO Z. CCA－secure proxy re－encryption without pairings［C］//Public Key Cryptography－PKC 2009： 12th International Conference on Practice and Theory in Public Key Cryptography， Irvine， CA， USA： Springer， 2009： 357-376.

［18］LIU W R， LIU J W， WU Q H， et al. Online/offline public－index predicate encryption for fine－grained mobile access control［C］//Computer Security－ESORICS 2016： 21st European Symposium on Research in Computer Security， Heraklion， Greece： Springer， 2016： 588-605.

［19］LIU X， YANG G， SUSILO W， et al. Privacy－preserving multi－keyword searchable encryption for distributed systems［J］. IEEE Transactions on Parallel and Distributed Systems， 2020， 32（3）： 561-574.

［20］ZHANG W， QIN B， DONG X， et al. Public－key encryption with bidirectional keyword search and its application to encrypted emails［J］. Computer Standards & Interfaces， 2021， 78： 103542.

［21］MIAO Y， MA J， LIU X， et al. Lightweight fine－grained search over encrypted data in fog computing［J］. IEEE Transactions on Services Computing， 2018， 12（5）： 772-785.

［22］CAO M S， WANG L H， QIN Z G， et al. A lightweight fine－grained search scheme over encrypted data in cloud－assisted wireless body area networks［J］. Wireless Communications and Mobile Computing， 2019， 2019： 9340808.

［23］MIAO Y， DENG R H， CHOO K K R， et al. Optimized verifiable fine－grained keyword search in dynamic multi－owner settings［J］. IEEE Transactions on Dependable and Secure Computing， 2019， 18（4）： 1804-1820.

［24］LIU X M， DENG R H， CHOO K K R， et al. An efficient privacy－preserving outsourced calculation toolkit with multiple keys［J］. IEEE Transactions on Information Forensics and Security， 2016， 11（11）： 2401-2414.

［25］SAMANTHULA B K， CHUN H， JIANG W. An efficient and probabilistic secure bit－decomposition［C］//Proceedings of the 8th ACM SIGSAC symposium on Information， computer and communications security， 2013： 541-546.

［26］KAMARA S， MOHASSEL P， RAYKOVA M. Outsourcing multi－party computation［J］. Cryptology ePrint Archive， 2011， 78： 103542.

（責任编辑：编辑郭芸婕）

收稿日期：2023-02-23

基金项目：河北省重点研发计划项目（22340701D），河北省自然科学基金项目（F2022201005）

作者简介：杜瑞忠（1975—）男，教授，从事可信计算与信息安全方向的研究，e－mail：durz@hbu.edu.cn。

*通信作者：杜瑞忠（1975—）男，河北大学教授、硕士生导师，从事可信计算与信息安全方向的研究，