四维不可压缩Navier-Stokes方程的能量守恒
王 斌, 周艳平, 别群益
(三峡大学 理学院, 湖北 宜昌 443002)
1 引言与预备知识
本文研究如下四维不可压缩Navier-Stokes方程的能量守恒:
(1)
其中,u表示速度场,π表示压力,ν表示黏性系数.Navier-Stokes方程描述的是黏性不可压缩流体动量守恒的运动方程,该方程解的存在性、稳定性、唯一性和解的非线性动力学特性等问题[1-6]是流体力学家近几十年来关注的热点.
1.1 能量弱解的定义
Leray[7]和Hopf[8]证明了在能量有限的初始条件下,Navier-Stokes方程存在弱解,可记为Leray-Hopf弱解.接着,Masuda[9]证明了在Ω⊂N中Navier-Stokes方程弱解的存在性.以下给出其定义.
定义1 对于初始值u0∈L2(N)和一个特定时间T,方程(1)中存在一个弱解使得


(2)

(3)
Foias[10]引入了函数空间Lq([0,T];Lp(N)),其中1≤p,q≤∞,证明了若Lq([0,T];Lp(N))中存在一个弱解u,满足
则u是Navier-Stokes方程的唯一弱解;Serrin[11]在N(2≤N≤4)的情况下也得到了一个类似的定理:对于1≤p,q≤∞,满足
则u是Navier-Stokes方程的唯一弱解.
1.2 适当弱解和部分正则性
在文献[12-14]中,Scheffer引入了Navier-Stokes方程的适当弱解和广义能量不等式的概念,并得到了这类弱解的各种部分正则性结果.随后,Wu[15]证明了四维空间中Navier-Stokes方程也存在适当弱解且满足局部能量不等式.以下给出适当弱解的定义(见文献[15]).
定义2 设(u,π)是Navier-Stokes方程在Q⊂4上的适当弱解,对于t∈[-1,0]使得
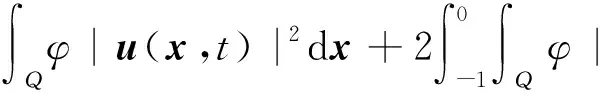
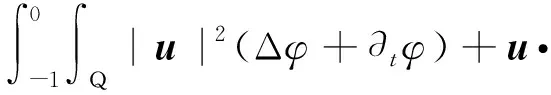
关于四维Navier-Stokes方程弱解的部分正则性研究已经取得了很多成果.Scheffer[13]证明了在4的局部闭集外存在弱解u是连续的,且该局部闭集的三维Hausdorff测度有限;Dong和Du[16]、Wang和Wu[17]均证明了奇异集的二维抛物型Hausdorff测度为0;接着,Wu[15]证明了在4×[0,∞]中Navier-Stokes方程存在部分正则性弱解满足局部能量不等式,且奇异集具有有限的二维抛物型Hausdorff测度.以下给出弱解的奇异集定义(可参考文献 [15]).
定义3 设u是Navier-Stokes方程在4×[0,T]上的弱解,若存在r>0,有u∈L∞(Qr(x),t),其中Qr(x,t)是以(x,t)为中心的时空柱面,则点(x,t)∈4×[0,∞]为正则点.否则(x,t)为奇异点,这里用S表示所有奇异点的闭集.
1.3 能量等式
若u是方程(1)的强解,则对所有t∈[0,T],方程(1)满足能量等式:
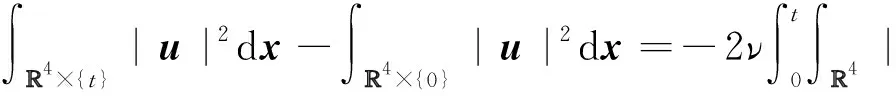
(4)
在Onsager猜想[18]下,等式(4)排除了由非线性项导致的异常能量耗散,该能量耗散与无黏性(ν=0)Euler方程的弱解有关.对于能量等式(4)的讨论,这里利用弱解的奇异集可能局限在一个低维时空子集的事实,通过Caffarelli-Kohn-Nirenberg定理[19]构建适当的覆盖奇异集的试验函数来建立能量等式.
关于Navier-Stokes方程的能量守恒已有很多研究结果,在三维空间中,Lions[20]证明了当u∈L4([0,T];L4(3))时等式(4)成立;Ladyženskaja、Solonnikov和Ural’ceva在文献[21]中也得到了这个结果;随后Kukavica[22]假设压力π∈L2([0,T];L2(3)),得到了能量守恒;在N维空间中,Serrin[11]证明了在u∈Lq([0,T];Lp(N))和2/q+N/p≤1的条件下能量守恒;Shinbrot[23]改进了这一结论,证明了当2/p+2/q≤1,p≥4时,该方程能量守恒.
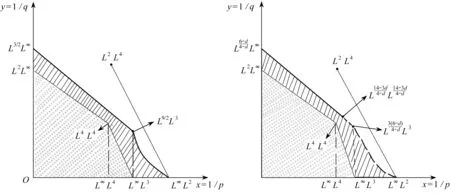
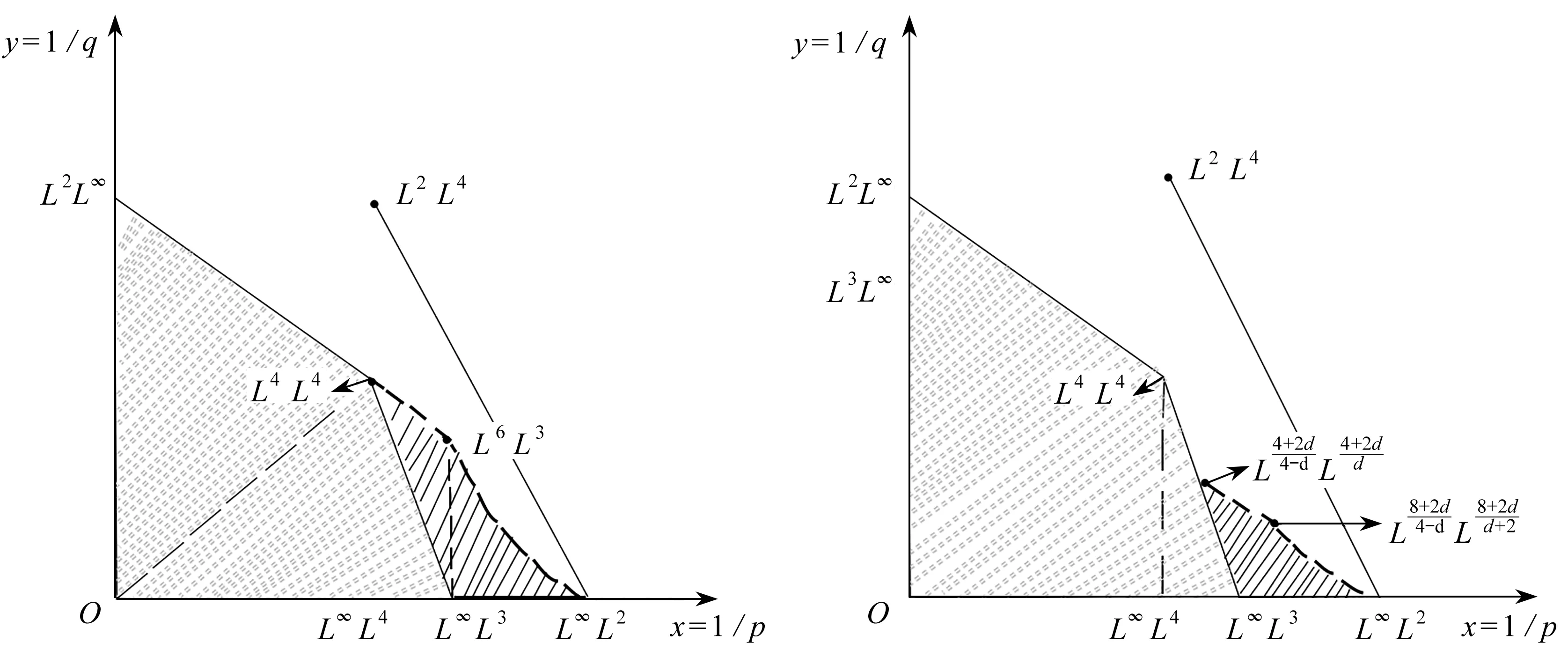
本文利用Wu[15]研究的四维不可压缩Navier-Stokes方程的部分正则性结果,得到了四维空间中新的Lq([0,T];Lp(4))条件,保证该方程的能量守恒.以x=1/p为横坐标,y=1/q为纵坐标绘图(见图1—4),图中虚线表示不包含边界,实线表示包含边界.
1.4 主要结果
定理1 假设u∈Cw([0,T];L2(4))∩L2([0,T];H1(4))是方程(1)在[0,T]上的适当弱解且在[0,T)上是正则的.若u∈Lq([0,T];Lp(4))满足下列条件:
(5)
(6)
(7)
则u在[0,T]上满足能量等式(4).
注1 定理1为奇异集的Hausdorff维数d=2时的情况(见后文中图3).
注2 若p<3,和文献[24]中三维情形时的结果比较可知: 在四维空间中, 当奇异集的Hausdorff维数d=2时, 式(7)为双曲线, 2xy+4x-4x2=1; 而在三维空间中, 其对应的曲线为抛物线, 6x2-7x-2y+2=0(此时d=1), 其中x=1/p,y=1/q.
2 证 明 思 路
下文中的Lq([0,T];Lp(4))均简记为Lq(Lp).假设(u,π)是Navier-Stokes方程在4×[0,T]上的一个Leray-Hopf弱解,类似文献[25],当0≤s (8) A-B-C=D+2P-2νE-2νF. (9) 本节主要目的是在试验函数φ中找出一个序列{φδ}δ>0,使得当δ→0时,A,B和E分别收敛到式(4)各项;C,F和D+2P趋于0,从而得到p和q的取值范围使得能量等式(4)成立. 给定一个Leray-Hopf弱解u和奇异集S,在试验函数中找到一个序列{φδ}δ>0,满足如下两个条件: (10) (11) 对于A,B和E的极限,若u∈L∞L2∩L2H1,由控制收敛定理,得 下文用 [-1,0] 来代替区间[0,T],0是临界点,假设S⊂4×{0}.为使C,D+2P和F趋于0,记Br(x)表示开球{y∈4:|y-x| (12) 因此,对任意的a>0,有 (13) 通过构建上面的试验函数φ,可得以下引理(其证明见文献[19]). (14) 其中,常数s不依赖于δ.另外,当d=0时,若sσ≤α,则式(14)仍成立. 如第2节所述,用 [-1,0] 来代替区间 [0,T].下面利用式(13)和引理1来分别估计C,F和D+2P.首先,对于C,由Hölder不等式,对任意的p,q≥2,有 (15) 有界.为此,令 根据引理1,当s≥1时,p和q须满足 (16) 另一方面,当s<1时,则p和q须满足 (17) 结合式(16)和(17),得C趋于0. 对于F,有 (18) 已知u∈L2H1,当δ→0时,|Q*|趋于0,可得式(18)最后一项趋于0.由Hölder不等式,对任意的p,q≥2,有 类似于C的估计,由引理1,得 (19) (20) 其中 结合式(19)和(20),得F趋于0. 对于D+2P,下面就p≥3和p<3两种情形分别讨论. (21) 类似于C的估计,由引理1,得 (22) (23) 其中 结合式(22)和(23),得D+2P趋于0. 当p<3时,由插值不等式,若 (24) (25) 得 (26) 其中 (27) 将式(25)代入式(27),得 (28) 上面的约束条件(16)和(17)、(19)和(20)、(22)和(23)分别表示三组平行线:线C、线F和线DP.线C围绕点L∞L2(即点(1/2,0), 后面类似)旋转, 线F围绕点L2L(8-2d)/(2-d)旋转, 且都随着α增大而逆时针旋转.当d≤2时,有α=(6-d)/2,此时线C和线DP重合;当d>2时,得α=2,此时线C和线F重合.因此,为保证能量守恒,p和q须满足如下条件: (29) (30) (31) 当p≥3时,若0≤d<2,考虑线C存在分离点L(14-3d)/(4-d)L(14-3d)/(4-d),若3≤p<(14-3d)/(4-d),线C为虚线,若p>(14-3d)/(4-d),线C为实线;当d=2时,线C、线F和线DP均为直线,2/p+2/q=1; 若2 当p<3时,线C和线F的约束条件不变,此时线DP为条件(28).联立式(16)、(17)和(28),并消去α,得到曲线: (32) 若d=2,代入式(32),得 此式为定理1的式(7)(见图3). 当2 图1—4分别表示奇异集Hausdorff维数d=0,0 图1 d=0图2 0 图3 d=2图4 2 具黏性不可压缩Navier-Stokes方程是流体运动的基本模型方程,有着重要的实际应用背景.Wu在文献[15]中研究了四维不可压缩Navier-Stokes方程的部分正则性,当该方程的Leray-Hopf弱解存在Hausdorff维数小于4的奇异集时,我们利用Wu[15]的结果,找到了四维空间中新的Lq([0,T];Lp(4))条件,从而解决了四维空间中紧性不足问题.关于Navier-Stokes方程适当弱解的能量守恒在三维和四维空间中已经有了很多研究,对于更高维空间里Navier-Stokes方程适当弱解的能量守恒的情形有待进一步研究.
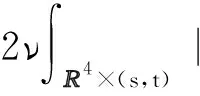
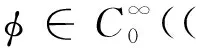
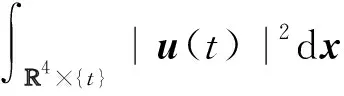

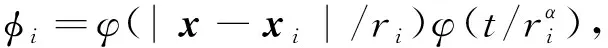

3 主要结果的证明
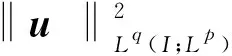


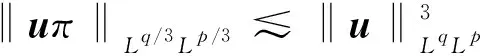
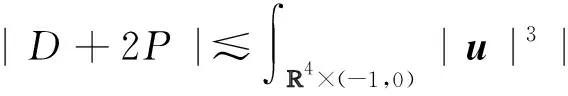
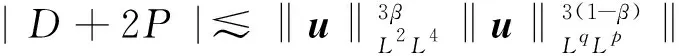
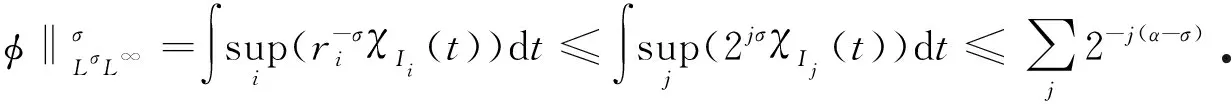
4 结 论

