无摩擦弹性接触问题的自适应交替方向乘子法

袁 欣, 张守贵

(重庆师范大学 数学科学学院, 重庆 401331)

0 引 言

弹性接触问题广泛存在于机械工程、土木工程等领域,比如堤坝的结合[1-3]等．弹性接触问题最大的特点就是具有很强的非线性性,这就使得理论分析和数值计算难以进行,一般只能通过一些适当的数值方法求得近似解,如常用的Uzawa算法[4-5]、交替方向乘子法[6-8]、 增广Lagrange法[9-10]和投影算法[11-12]等．这些方法利用变分不等式理论,将非线性弹性接触问题转化为一个对应的线性变分形式进行迭代求解．本文研究的是一个由区域Ω代表的线性弹性体和一个刚性基础支撑的弹性接触问题,其中Ω∈R2．区域Ω的边界Γ(Γ=ΓD∪ΓN∪ΓC)是光滑的．假设弹性体固定在ΓD上,且mean(ΓD)>0．边界ΓC是Γ的一部分,它也是Ω和基础支撑的接触面．ΓC和刚性基础支撑之间的障碍函数用g表示．在本文中考虑很小的形变,应变张量为(u)=(∇u+∇uT)/2,其中u=(u1(x),…,ud(x))为位移场．根据Hooke定律可知,应力张量和位移场的线性关系为

σ(u)=C(u),

其中C=(Cijkl)是(四阶)弹性模张量,它是对称正定的．设n表示Ω在Γ上的单位外法向量,t表示Ω在Γ上的单位切向量,则

un=u·n,ut=u-unn,

σn(u)=(σn(u)n)·n,σt(u)=σ(u)n-σn(u)n．

考虑弹性接触问题[7-8],即寻找位移场u满足以下条件:

(1)

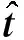
1 增广Lagrange乘子法

为了方便后面叙述,先引入以下记号:

V={v∈H1(Ω)2,v=0, onΓD},

K={v∈V,vn-g≤0, onΓC},

双线性形式为

根据文献[7]可知,弹性接触问题(1)可以转化为限制性极小值问题,寻找u∈K满足不等式:

J(u)≤J(v), ∀v∈K．

(2)

由文献[1,9]可引入Lagrange乘子λ∈L2(Ω),得问题(1)的变分形式:

a(u,v)=l(v)-(λ,vn),

(3)

其中双线性形式在V×V上满足以下条件:

α的选取不依赖于u的选取,且均大于零．

为了通过交替方向乘子法解决问题(2),需要构造一个用增广Lagrange函数表示的鞍点问题．根据文献[13],定义集合

所以问题(2)就等价于下面的限制性极小值问题,寻找(u,p)∈V×L2(ΓC)满足

(4)

un-p=0．

(5)

根据式(4)和(5)可以得到增广Lagrange函数:

(6)

其中ρ>0为罚参数．考虑由式(6)表示如下鞍点问题:

Lρ(u,p;μ)≤Lρ(u,p;λ)≤Lρ(v,q;λ), ∀{v,q;λ}∈V×L2(ΓC)×L2(ΓC),

(7)

然后可以求解问题(2)和(7)．

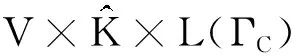
由引理1和文献[6-8]中的交替方向乘子法(ADMM1)可知,要想求解问题(2),只需要求解增广Lagrange函数Lρ的鞍点{u,p;λ}．即先由给定的初始值和迭代公式计算位移,再计算辅助变量,最后更新Lagrange乘子,以此顺序迭代直至达到终止条件．

由文献[13-14]知,可以通过改变辅助变量和位移场的计算顺序对算法进行优化,并采用交替方向乘子法计算该鞍点问题．算法过程如下:

第1步 给定初始值{u0,λ0}∈V×L2(ΓC),ρ>0,置k=0．

第2步 求辅助变量pk+1∈L2(ΓC):

Lρ(uk,pk+1;λk)≤Lρ(uk,q;λk), ∀q∈L2(ΓC)．

(8)

第3步 求解位移uk+1∈V:

Lρ(uk+1,pk+1;λk)≤Lρ(v,pk+1;λk), ∀v∈V．

(9)

第4步 更新Lagrange乘子:

(10)

算法1 交替方向乘子法(ADMM2)

第1步 给定初始值λ0,u0,ρ>0,置k=0．

第2步 计算辅助变量pk+1∈L2(ΓC):

(11)

第3步 计算位移uk+1∈V:

(12)

第4步 计算Lagrange乘子:

(13)

第5步 给定某种判定条件,若满足则停止迭代得到数值解uk+1; 否则,置k=k+1,返回第2 步．

2 自适应交替方向乘子法

我们注意到算法1对任何固定的罚参数ρ>0都是无条件收敛的[14]．但是,如果罚参数过大或者过小,都会影响算法的收敛速度．为了改善算法的性能,我们对罚参数应用了自适应法,则得到可变罚参数ρk．接下来我们假设一个非负序列{sk},满足

在算法1中让罚参数在迭代过程中自动选取,可以得到如下罚参数自适应交替方向乘子法(SADMM),由此得到变参数序列{ρk},以此序列代替固定参数ρ．

算法2 自适应交替方向乘子法(SADMM)

第1步 给定初始值λ0,u0,ρ>0,罚参数ρ0=ρ,置k=0．

第2步 计算辅助变量pk+1∈L2(ΓC):

(14)

第3步 计算位移uk+1∈V:

(15)

第4步 计算Lagrange乘子:

(16)

第5步 选取罚参数ρk+1,使得

(17)

第6步 给定某种判定条件,若满足则停止迭代得到数值解uk+1; 否则,置k=k+1,返回第2步．

为了证明算法2的收敛性,先给出以下引理和定理．

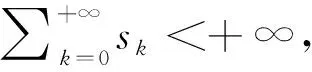
定义以下符号:

由算法2的第5步可知,罚参数ρk∈[ρ0/Cs,Csρ0]是有界的,设

根据算法的原理和问题的性质,可得算法2的收敛结果．

定理1 设{(uk,pk),λk}是由算法2产生的序列,则有

其中{u,λ}是问题(3)的解．

证明令δuk=uk-u,δpk=pk-p,δλk=λk-λ,根据式(3)和(15)可得

两式相减可得

即

(18)

在式(18)中取v=δuk+1,则

(19)

由于p=un在ΓC上成立,则代入式(19)得到

(20)

而且由式(16)有

因此由以上两式,并根据双线性形式a(·,·)的性质可知

(21)

因为在边界ΓC上有λ≥0,un-g≤0,(un-g,λ)ΓC=0成立,由此可得到以下两个不等式:

(22)

(23)

由式(22)、(23)可得

(24)

由式(14)有

代入式(24)可以得到

化简可得

变换化简得到

(25)

由式(16)和p=un在ΓC上成立,可得

即

整理等式两边后得到

两边同时取范数并由式(25)可得

即定理得证．

定理2 设{uk,pk,λk}是算法2产生的序列,则在V上uk→u,在L2(ΓC)上pk→p,在L2(ΓC)上λk⇀λ．证明由于sk≥0, 0<ρk+1≤(1+sk)ρk,可得

(26)

由定理1可知

从而由式(26)有

(27)

由式(21)和(27)可得

(28)

即存在一个常数C>0使得下面不等式成立:

(29)

根据式(27)可得

(30)

由式(21)、(27)和(30),结合式(21),我们可以得到

(31)

由级数收敛的必要条件可知

所以在V上,uk→u．因为在边界ΓC上有p=un,则

所以在L2(ΓC)上有pk+1→p．

对于任意k≥1,由于

所以可以得到

结合式(21)可得序列{λk}是有界序列,可证λk⇀λ[14]．从而定理得证．

综上,算法2的收敛性得证．

注1 若在算法2的第5步中令sk=0,则ρk=ρ0．因此算法2为固定罚参数情形,即为算法1,故同理可证算法1也是收敛的．

3 罚参数的自适应法则

利用自适应交替方向乘子法求解无摩擦单侧弹性接触问题,迭代过程中通过迭代函数自动调整罚参数,用变参数ρk代替固定参数ρ[10-11,14-15],从而达到提高算法效率的目的．下面具体考虑算法2中选取罚参数ρk的自适应法则．由定理1 的结论可知序列{uk,pk,λk}满足以下不等式:

为了提高算法的收敛速度,利用如下平衡原理:

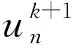
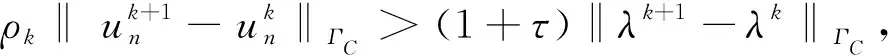
其中

即序列ρk满足

序列{sk}按照如下方式得到:

其中cmax是一个正常数,ck表示ρk改变的次数,即

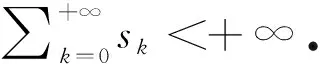
4 算 例 分 析

本文使用FreeFEM++软件求解算例的位移场、迭代次数和CPU运行时间．该软件可以对二维和三维偏微分问题自动建立有限元模型,我们只需要在此基础上定义网格和问题即可进行求解．

为了验证算法的有效性,我们给出两个数值算例．在数值算例中,我们取τ=2和cmax=100．对所有数值结算都采用迭代终止条件‖uk+1-uk‖≤10-5‖uk+1‖．

算例1 设Ω=(0,2)×(0,1)是一个矩形的弹性体,边界由ΓD={0}×(0,1),ΓN1=(0,2)×{1},ΓN2={2}×(0,1)和ΓC=(0,2)×{0}四部分组成．弹性体在ΓD上固定不动,即u=0,在ΓN1上满足Riemann边界条件σ(u)n=(0,-10)T,在ΓN2上满足σ(u)n=0．在ΓC上,弹性体Ω和刚性基础支撑之间的障碍函数g(x)=0.01．材料常数即弹性模量和Poisson比分别为2 000和0.3．

图1 形变后的弹性体及障碍函数(算例1)图2 g=0.01时的算法迭代次数Fig. 1 The deformed configuration and the Fig. 2 The number of iterations for each obstacle function (example 1)method with g=0.01

表1 g=0.01时3种算法的CPU运行时间

用算法2求解此算例得到弹性体形变图,如图1所示(数据扩大为原来的10倍)．为了展示算法的性能,对3种算法(ADMM1(文献[8]中的算法1),ADMM2(本文中的算法1),SADMM(本文中的算法2))取相同的初始罚参数和步长h=20,考察了迭代收敛速度,如图2所示．显然,固定罚参数的交替方向乘子法(ADMM1、ADMM2)对参数的取值非常敏感,数值过大或过小都会减缓算法的收敛速度．而SADMM的罚参数自动选取,在很大程度上解决了算法对参数取值的依赖性．

取不同的初始罚参数ρ和步长h, 采用3种算法对问题进行数值计算, 所需的CPU运行时间如表1所示．图1和表1中数值结果均表明,自适应交替方向乘子法收敛速度及运行速度明显优于固定罚参数交替方向乘子法,并且对所有的罚参数具有较好的稳定性．

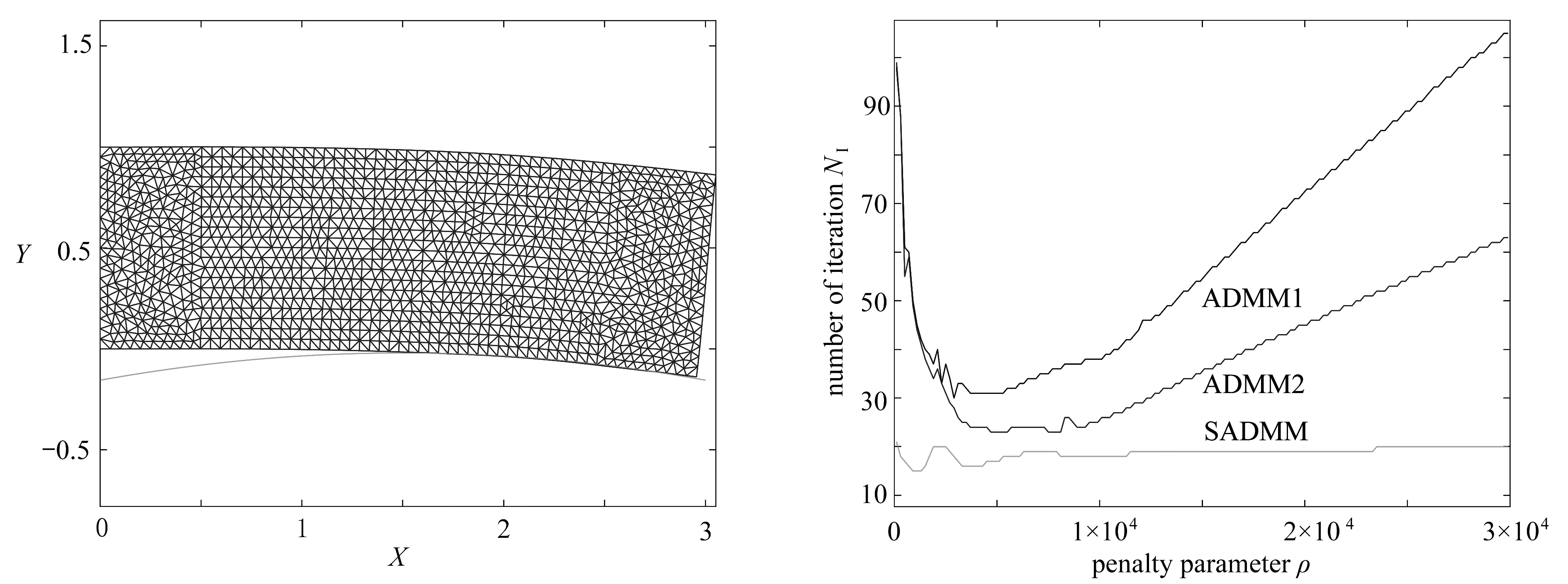
图3 形变后的弹性体及障碍函数(算例2)图4 各算法的迭代次数Fig. 3 The deformed configuration and the obstacle Fig. 4 The number of iterations for each method function (example 2)

表2 3种算法的CPU运行时间

对此算例应用算法2得到形变后的弹性体,如图3所示(数据扩大为原来的20倍)．对3种算法(ADMM1、ADMM2、SADMM) 取不同的初始罚参数ρ和步长h=20,考察算法收敛速度,数值结果如图4所示．从数值结果可以看出,ADMM2比ADMM1的迭代次数更少,但是还是没有摆脱对罚参数的依赖性．而SADMM相对比较稳定,不会因为罚参数的过大或者过小而显著增加迭代次数．为了更全面展示SADMM的性能,分别取不同的初始罚参数ρ和步长h,考察3种算法的CPU运行时间,如表2所示．结果表明自适应交替方向乘子法具有较好的性能．

5 结 论

本文提出了求解弹性接触问题的自适应交替方向乘子法,该算法不仅计算简单,并且给出的自适应法则利用边界迭代函数自动选择合适的罚参数,能有效解决交替方向乘子法的迭代次数高度依赖于罚参数ρ的问题,从而显著提高算法性能．数值结果表明了该算法的有效性．