直齿锥齿轮分岔脱啮特性参数解域界结构

田亚平, 杨江辉, 王瑞邦

(兰州交通大学 机电工程学院, 兰州 730070)

0 引 言

锥齿轮传动广泛应用于机车、航空、机床等行业传动装置中．含间隙和时变因素的锥齿轮传动系统的非线性振动对系统运动的稳定性提出了严峻挑战,成为学者们研究的热点．王三民等[1]建立了正交锥齿轮系统动力学模型并分析了系统分岔和幅值跳跃特性．黄康等[2]考虑随机因素探索了间隙的合理范围．Wang等[3]考虑含齿面混合润滑研究了表面粗糙度对齿面冲击的影响．Hua等[4]建立了轴承-锥齿轮转子有限元模型,分析了轴承支承刚度对动态啮合力的影响．Cao等[5]分析了不同润滑状态下锥齿轮传动系统的非线性动态特性．李飞等[6]研究了摩擦和重合度对系统振动幅值和啮合力的影响．

小波法[7]、数值法[8]是求解非线性系统分岔特性的常用方法,但在全局分岔特性转迁特性分析上适用性较差．胞映射理论是研究非线性动态特性转迁的常见方法．在参数域平面内,Gou等[9]采用胞映射研究了齿轮副模型的周期吸引子分形结构,Liu等[10]通过对齿轮解域界分析实现了混沌控制,林何等[11]分析了弧齿锥齿轮传动系统中周期运动的解域界结构．因伪不动点周期求解及追踪CPNF法求解效率高,在含间隙的行星轮系[12]和单级齿轮系统[13]的周期求解中获得了成功应用．田亚平等[14]用CPNF法研究了单级齿轮系统的动态特性解域界结构．多参耦合下的解域界结构能有效揭示其动态特性间的耦合及转迁规律．目前,针对含间隙直齿锥齿轮动态特性参数解域界结构的研究还鲜有报道．

据统计,间隙和时变参数是导致动车齿轮传递装置(图1)故障和车辆振动超标的主要因素．本文以该锥齿轮传动系统为研究对象,建立了7自由度锥齿轮系统动力学模型,采用CPNF法求解周期、脱啮、齿面冲击、动载特性的转迁规律,探索参数组合下系统的周期分岔与齿面冲击及脱啮、动载间的耦合关系,为锥齿轮结构设计参数选择提供理论依据．

1 动力学模型

含弹性支承的直齿锥齿轮传动系统动力学模型如图2所示[1]．两齿轮轴线正交于原点O,建立坐标系∑:{Oxyz}．两轮支承等效在齿宽中点O1,O2,沿坐标轴的支承刚度和阻尼为kij,cij(i=x,y,z;j=1,2)．ch,kh(t)和bh分别为齿轮副啮合的阻尼、时变刚度和齿侧间隙．设主动轮1受到的驱动力矩Tp由常量Tpm和变量Tpv构成;从动轮2受到稳定的阻抗力矩Tgm．忽略齿轮的摆动与弯曲,两个刚性锥盘的振动是分别以O1,O2为中心,沿坐标轴的移动和轴线的转动,即8个自由度{X1,Y1,Z1,X2,Y2,Z2,θ1,θ2}．

考虑振动和误差,两齿轮沿啮合线的动态综合传递误差Λn为

Λn=(X1-X2)a1-(Y1-Y2)a2-(Z1+r1θ1-Z2-r2θ2)a3-en(t),

(1)

式中,a1=cosδ1sinαn,a2=cosδ1cosαn,a3=cosαn,δ1为主动轮节锥角,αn为法面压力角,r1,r2为两轮的节圆半径．齿轮副的静态综合误差en(t)展开成级数形式为

(2)

式中,Ωh,Al和Φl为啮合频率、l阶谐波幅值和初相位．

齿轮副的啮合力Fn及其沿坐标轴的分力Fx,Fy和Fz分别为

(3)

用文献[15]计算kh(t)并用级数展开为

(4)

式中,km,kkl和Φkl为啮合刚度的均值、l阶谐波幅值和初相位．结合动车齿轮箱工程计算精度要求,本文选取一阶级数进行数值仿真计算．

间隙函数f(Λn)为

(5)

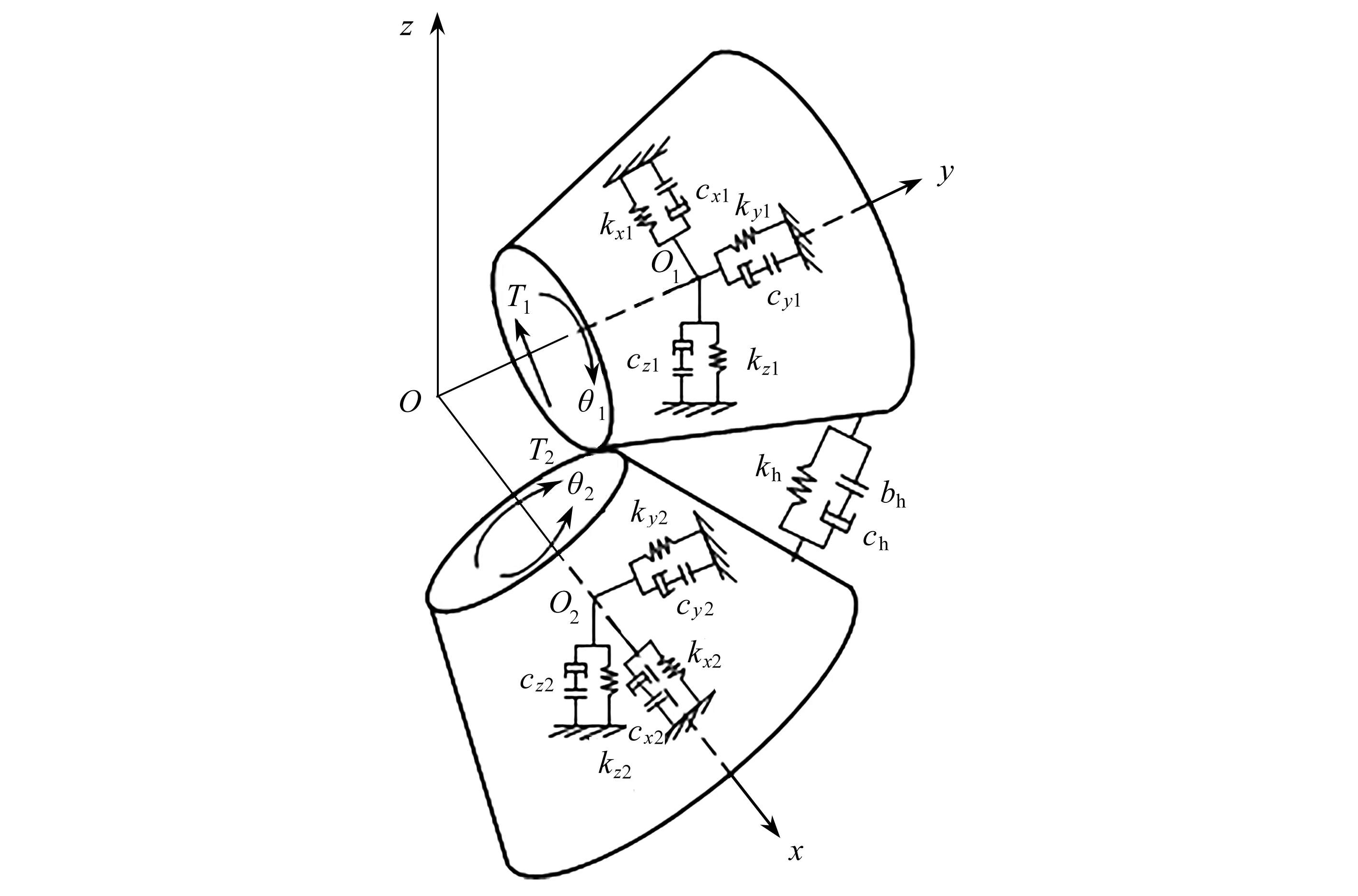
图2 动力学模型Fig. 2 The nonlinear dynamic model for a spiral bevel gear set

根据Newton第二定律,图2所示的锥齿轮传动系统振动方程为

(6)

式中,m1,m2,J1,J2为两轮的质量和转动惯量．

用沿啮合线的动态综合传递误差Λn作为新自由度,将式(6)中两齿轮扭振方程合并得

(7)

将上述方程整理并量纲一化处理得

(8)

式中

xj=Xj/bn,yj=Yj/bn,zj=Zj/bn,λ=Λn/bn,Ωn=(km/me)1/2,

Ωij=(kij/mj)1/2,ξij=cij/(2mjΩn),kij= (Ωj/Ωn)2,i=x,y,z,j=1,2,

(9)

bn为标称间隙．

2 系统动态特性仿真指标

2.1 脱啮占空比和齿背啮合比

轮齿脱啮和齿背接触行为是引起齿面拍击和附加动载荷的主要因素．由文献[16]知,齿轮啮合的冲击和脱啮(I=0,1,2)状态可由运动周期中的最小啮合综合误差λmin与齿侧间隙b判断,其判断式为

(10)

脱啮占空比(non-meshing duty coefficient,δNMDC)和齿背啮合比(back-meshing duty coefficient,δBMDC)是量化系统脱啮冲击严重性的主要指标,设在一个运动周期T内脱啮时间为t1,齿背啮合时间为t2,则δNMDC和δBMDC为

(11)

2.2 动载系数

齿轮强度设计中考虑齿轮振动导致动态啮合力瞬态增大的因数称为动载系数(dynamic load coefficient,δDLC)．受支承刚度、箱体结构和重合度等因素影响动载系数计算十分复杂,为突出间隙和时变刚度对动载系数的影响,定义运动周期内最大啮合力|fn(τ)|max与平均值fpm之比的平方根为动载系数:

(12)

3 参数解域结构求解

参数解域结构求解是基于胞映射原理将参数平面进行胞元离散,在胞元内对周期运动采用CPNF法延续追踪判稳获得其周期运动的参数域界结构．在追踪过程中伴随有脱啮、冲击和动载特性的参数解域结构求解．其基本思想及实施过程如下．

3.1 参数域胞元化

对多参γi控制的非自治动力学系统可描述为

(13)

式中,X为n维状态向量,τ为量纲一时间,γi∈RK为系统的k个控制参数,f为映射法则．

为分析激励参数γi与响应间的关联机制,在[xl,xu]×[yl,yu]二维参数域Θ内对参数离散化为n×m个胞元,参数胞为cij(i=1,2,…,n;j=1,2,…,m)．其中,xl,yl和xu,yu分别表示x,y方向的起点和终点,hi,hj为离散胞在x,y方向的胞元尺度．x,y方向的胞尺度hi,hj为

(14)

在参数域Θ内,从xl,yl开始得到x,y方向上参数的递推关系xi,yj为

(15)

则域Θ内离散后的各胞元(xi,yj)赋值为

(16)

3.2 动力学行为延拓追踪步骤

参数域Θ内各胞元的动力学行为采用CPNF法追踪求解．首先沿x方向对初始胞元(x0,yj)用伪不动点PNF法[10-11]进行系统运动周期求解并判稳; 然后沿x方向按步长hi进行延拓追踪、用Floquet乘子|λ|max判断周期运动的稳定性．当|λ|max>1时周期运动失稳,在该胞元(xi,yj)处终止周期追踪判断分岔类型,并用PNF法重新求解新周期,若求解周期数超过设定值时认定该胞元为混沌或拟周期状态(可用Floquet乘子和Lyapunov指数判定),在(xi+1,yj)胞元处重新求解周期数并追踪直至xu结束;当完成x方向追踪后,沿y方向递进一层继续追踪求解,直至遍历全域结束．

3.3 胞元周期解求解过程

CPNF法周期求解判稳的关键是求方程组(17)的稳定解

(17)

式中,Φ=DP(X)为系统的转迁矩阵[12], 其状态方程的Jacobi矩阵∂f(X,τ)/∂X在λ≠±b的分段光滑区内为

(18)

式中

A1=[-a1[kx12ξx1],a2[ky12ξy1],a3[kz12ξz1],

a4[kx22ξx2],-a5[ky22ξy2],-a3[kz22ξz2]],

(19)

因在λ=±b处Jacobi矩阵不存在,故结合计算精度选取合理步长的有限差分法替代为

(20)

方程(17)以(Xk,I)为初值积分一个周期T获得系统迭代点Xk+1和转迁矩阵DP(Xk)．令Xk=Xk+1作为下次迭代的初始值,迭代到满足精度要求的不动点XF,就是式(13)的m倍周期运动X(τ)的不动点．找到稳定周期解后,引入分岔参数Ω,采用延续追踪法进行周期追踪．设已求得Ω=Ωk(k=0, 1, 2, …)时,周期T的不动点为Xk,用Euler积分法得Ω=Ωk+1点对应不动点Xk+1的初始不动点Xk+1,0的预测公式[14]:

(21)

式中,ΔΩ为追踪步长,GX(Ωk,Xk)=I-DP(Ωk,Xk),GΩ(Ωk,Xk)=PΩ(Ωk,Xk)．PΩ(Ωk,Xk)由打靶法建立的微分方程组(22)求得

(22)

式中

fΩ(X,Ω,τ)=feΩ{2cos(Ωτ)+Ωsin(Ωτ)}[01×131]T+

αsin(Ωτ)[0 -1 0 1 0 1 0 1 0 -1 0 -1 0 -4]T/4．

(23)

以(Xk,Ωk)为初值积分一个映射周期T获得以(Xk,PΩ(Ωk,Xk))为追踪参数下的新不动点．

4 系统动态特性综合分析与解域界

不失一般性,取量纲一仿真参数:

ξi1=ξi2=0.01 (i=x,y,z),ξh1=ξh2=0.012 5,ξh=0.05,

ki1=ki2=1.0,kh1=kh2= 0.5,kh=1+αcos(Ωτ),

fpm=0.5,fav=0.0,fe= 0.2,b=1.0．

在参数解域界平面内,齿面冲击/运动周期(I/P)类型用特定的颜色表示,其分岔曲线为解域界．齿轮系统常常稳定运行于短周期状态下,为突出低周期(P<64)分岔特性,在I/P分岔图中对周期数P≥65的长周期、拟周期(quasi-P)和混沌(chaos)运动均用“I/N”表示．系统的倍化(PD bif)、鞍结(NS bif)、檫切[17](G bif)分岔定义参见文献[14],不再赘述．当系统从I/P向I/(3P)状态转迁时,系统发生了齿轮系统典型的周期3分岔(3T bif),依次类推．

时变啮合刚度系数α表征齿轮啮合重合度,其值表征单双对齿啮合不均匀性程度．频率比Ω表征系统转速,其值表征系统转速高低．故构建Ω×α∈[1.2, 1.7]×[0.05, 0.55]参数平面(图3),在平面内均匀地选取501×501个胞元构建I/P及相应的δNMDC,δBMDC,δDLC解域界结构．

I/P解域界结构(图3(a))表明:在参数平面内,以周期1(P=1,下同)运动为主,存在P=2,3,9,10,18,32和quasi-P、chaos等运动状态;3种齿面冲击共存,以单边冲击为主．在α<0.15区域内,随Ω递增系统发生了SN bif和3T bif,使系统处于0/1,1/1,1/3运动状态．在0.15<α<0.3区域内,系统通过PD bif、3T bif、HP bif等分岔方式进入混沌运动．在0.3<α<0.55区域内,随Ω递增系统发生了G bif、3T bif、3T chaos和CIC bif 等分岔．在Ω=1.6附近表现出复杂的动力学行为转迁,即在该胞元内动力学行为极其不稳定．沿α方向在Ω<1.25区间内,系统以P=1运动的3种冲击转迁为主．在1.25<Ω<1.5区间,系统的动力学行为较为稳定．当Ω>1.5时,系统通过HP bif、3T bif和CIC bif的形式使系处于周期-混沌-周期运动状态．参数解域界结构表明齿轮啮合重合度是影响齿轮冲击的主要因素,随α递增齿面脱啮、齿背接触的概率增大．在系统的共振频率附近多周期、混沌现象加剧,并出现了齿轮传动系统典型的周期3分岔行为．

系统I/P解域界结构对应的齿面脱啮、齿背接触和动载特性如图3(b)—3(d)所示．图3(b)表明,齿轮脱啮程度随周期分岔和齿面冲击的转迁而阶跃突变,在1/1解域内其脱啮程度并不一致,在G bif分岔线附近δNMDC达到极值0.55左右．随α增大其脱啮程度加剧,而在1/N和2/N解域内δNMDC值并未达到极值,即多周期或混沌运动下齿面脱啮未必最严重．图3(c)表明,在双边冲击的2/1域界内其齿背接触最为严重达到极值0.38左右,在2/3、2/N域界内其齿背接触状态随α递增而加剧但没有达到极值,即齿轮啮合的双边冲击程度与系统混沌现象并无必然联系．图3(d)表明,系统的δDLC随齿面冲击和周期运动分岔出现了突变,在同一解域内其动载系数随α递增而增大,在无冲击的0/1解域内其值较小、在双边冲击的2/1、2/N域界内达到极值2.8．

(a) I/P(b) δNMDC

(c) δBMDC(d) δDLC图3 Ω×α平面动态特性解域界结构Fig. 3 Dynamic properties solution domain boundary structures in the Ω×α 2-parameter plane

为验证CPNF法求解的正确性,沿α方向以0.05等距选取截面,用Runge-Kutta法对Ω参数分岔进行数值计算获得三维I/P分岔图(图4)．

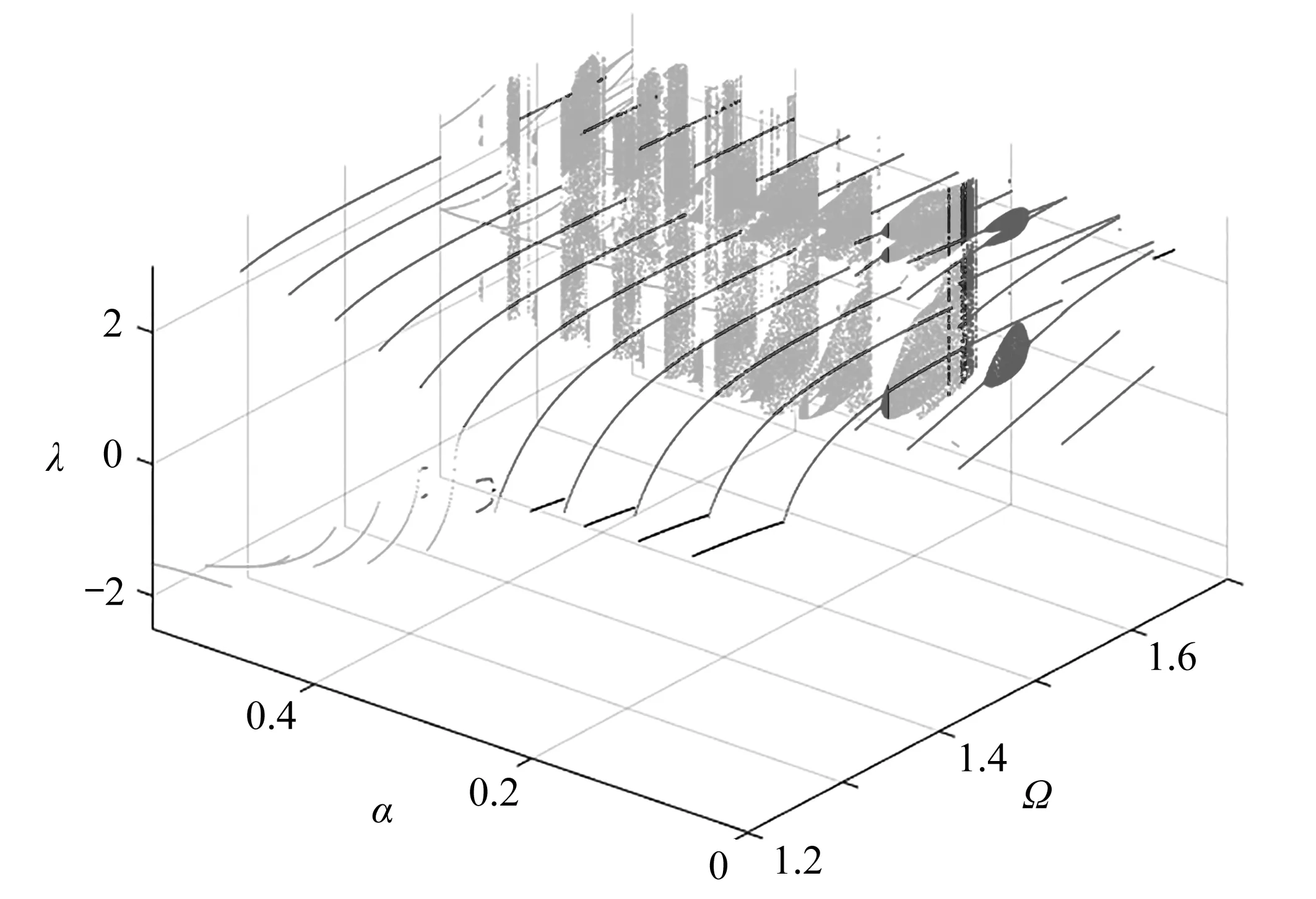
图4 Ω×α双参分岔图Fig. 4 The bifurcation diagram in the Ω×α 2-parameter plane

图4中,黑、红、蓝色映射点分别对应无冲击、单边冲击和双边冲击,其I/P分岔过程与图3(a)相匹配验证了解界域结构的正确性．因CPNF法对周期运动求解追踪过程不用计算瞬态,故较Runge-Kutta法求解效率高．

为更清晰地展示周期分岔与齿面脱啮的关联关系,取α=0.20,0.40的分岔图如图5所示．图5(a)中的系统通过SN bif、3T bif、HP bif和激变(CIC bif)分岔方式使系统处于0/1, 1/1, 2/3, 1/3, quasi-P,2/chaos,1/chaos,1/1运动．图5(b)中系统通过SN bif、3T bif、PD bif和C bif分岔使系统处于2/1,1/1,2/3,2/chaos运动状态．HP bif和SN bif可通过CPNF追踪中Floquet乘子|λ|max来判定,而G bif与SN bif是通过齿面冲击类型和Floquet乘子共同判别,若穿越λ=±b截面时Floquet乘子从实数轴方向穿越单位圆则发生了鞍结分岔,否则为擦切分岔．

取α=0.20截面(图5(a))的部分Poincaré映射和相图(图6)验证CPNF求解的分岔过程．Ω=1.531时系统为1/1运动(图6(a))经3T分岔为2/3运动(图6(b)),P=3转迁为3个焦点(图6(c))、Hopf圈(图6(d))、扭曲锁相(图6(e))直至形成混沌运动(图6(f))．即图5验证了通过周期3分岔和Hopf分岔使系统处于1/1,2/3,1/1,拟周期和混沌运动．

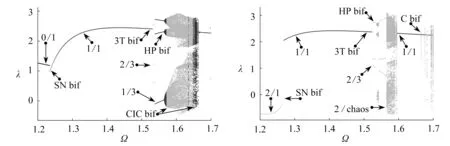
(a) α=0.20(b) α=0.40图5 分岔图Fig. 5 The bifurcation diagram via α

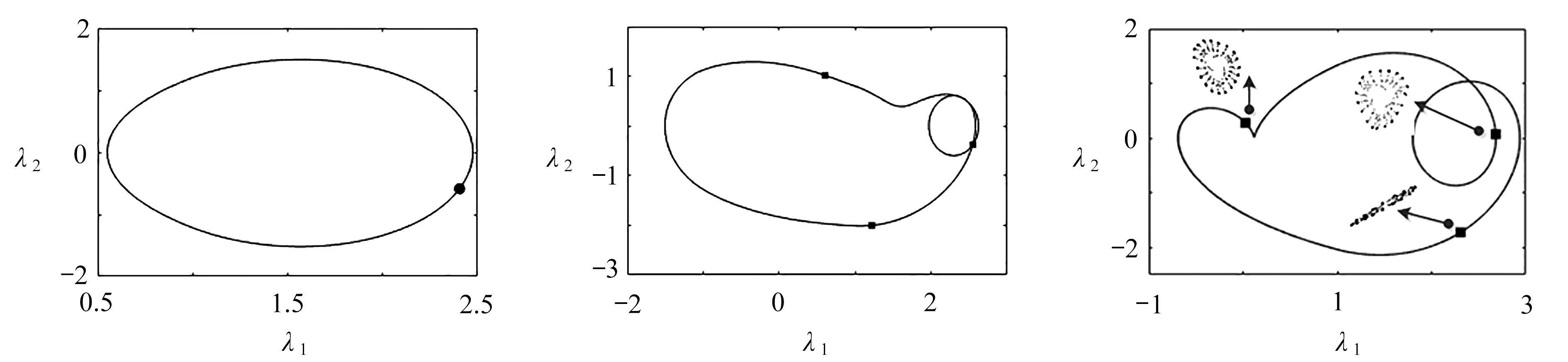
(a) Ω=1.531(b) Ω=1.535(c) Ω=1.563

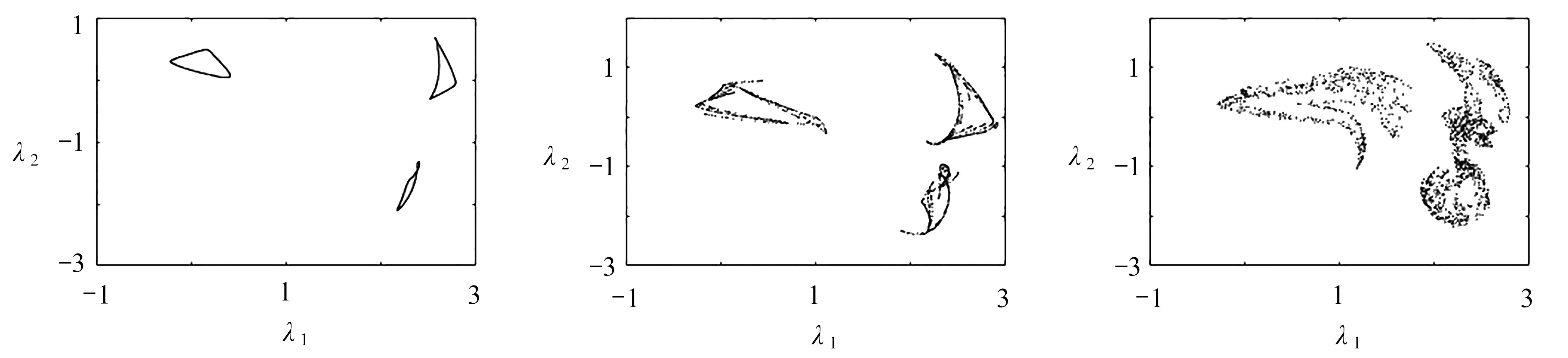
(d) Ω=1.575(e) Ω=1.600(f) Ω=1.650图6 Poincaré映射图和相图Fig. 6 Poincaré and phase maps

图7为图5(b)中α=0.40时I/P部分的Poincaré映射和相图．Ω=1.523时系统处于0/1运动(图7(a))经周期3分岔为2/3运动(图7(b)),P=3再经周期3分岔为P=9(图7(c))、P=18(图7(d))、……、混沌运动(图7(e))．图7验证了系统经周期3分岔进入混沌的过程．

取α=0.40截面(图5(b))对应的齿面脱啮比、齿背接触比和动载系数分布图(图8)．齿面脱啮在齿面冲击转迁截面发生了突变,在1/1周期区间其脱啮程度随Ω递增而减弱(图8(a))．齿背接触在双边冲击区域随Ω递增而加剧,在阵发性混沌区域存在突变现象(图8(b))．动载系数随齿面冲击和周期分岔产生了突变,随齿面冲击加剧其动载系数俱增(图8(c)),在单边冲击区其δDLC随Ω递增而递减,在双边冲击区随Ω递增而递增．即齿面冲击和周期分岔是影响齿面脱啮、齿背接触及动载特性的主要因素．

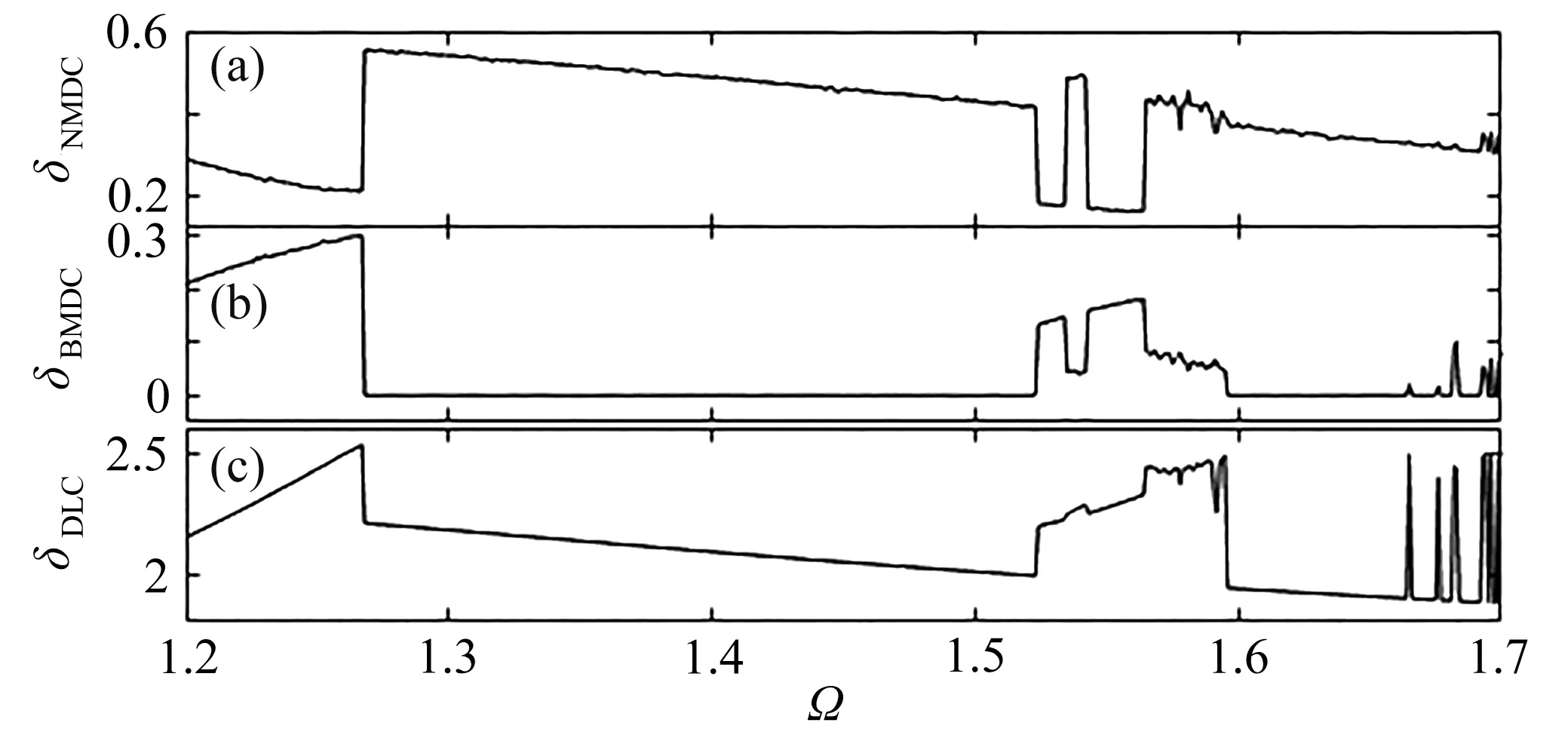
图8 脱啮比、动载系数分布图Fig. 8 The δNMDC, δBMDC and δDLC distribution diagrams

时变啮合刚度和频率比平面内的I/P,δDLC,δBMDC和δNMDC解域界结构揭示了系统随参数分岔、脱啮、冲击、动载荷的转迁规律及其关联关系．针对不同速度车型要求,依据解域界结构对转速和重合度参数进行匹配优化．选取参数时尽量避开混沌、双边冲击和动载较大的参数区域,尽可能在0/1区域选择合理的重合度或转速参数能有效地降低啮合冲击、脱啮和动载对齿轮箱的影响,可延长齿轮箱的服役周期、降低设备维护费用．

5 结 论

本文针对7自由度直齿锥齿轮传动系统的周期分岔、齿面冲击、脱啮和动载特性问题,采用胞映射理论构建了重合度和转速激励参数平面,用CPNF法进行了数值求解获得了I/P,δNMDC,δBMDC和δDLC解界域结构,得到了如下结论:

1) 参数平面内基于胞映射理论的CPNF法解域界结构求解方法是一种高效的数值求解方法．

2) 含间隙的锥齿轮系统存在鞍结、倍化、Hopf、激变、擦切和周期3等分岔现象,随时变啮合刚度系数增加其齿面冲击加剧,在啮频附近系统的周期运动和齿面冲击最为严重．

3) 系统分岔和齿面冲击转迁导致其齿面脱啮和齿背接触及动载行为产生了突变,在各I/P区域内其值也随参数波动．随时变啮合刚度系数增大其动态特性加剧．在1/1和2/N区域其脱啮最为严重,在2/1区域内齿背接触最为严重,其动载系数最大．