一种改进的PSO算法在含高比例风电系统中的应用

唐京瑞　陈勇

关键词： 高比例风电 HCSN-PSO 算法 条件风险价值 多目标 机组组合

中图分类号： TM614 文献标识码： A 文章编号： 1672-3791（2023）15-0010-06

21 世纪以来，能源与环境问题已成为全世界共同关注的话题，面对传统能源对自然环境引起的气候变化，发展高比例可再生资源越来越备受青睐。中国能源发展相关报告指出，到2040 年可再生能源發电量将占到新增发电量的50％， 但可再生能源存在能量密度低、间歇性明显、分布分散等特点，在接入传统能源电力网络中很难适应现有机制[1]。随着系统内联合运行的机组也在不断扩大，加之可再生能源的冲击和不同的机组具有不同的能量转换特性等因素，传统的单目标机组组合优化模型和算法已经难以适用。

高比例风电机组的优化组合是指系统在满足功率平衡、机组安全、开停机时间和风电场的出力等各种约束条件下，根据负荷要求，对一个调度周期内各个时段上的运行状态进行优化，确定出某一时段内给定负荷下机组的最优出力，使周期内的总成本（包括发电成本和弃风成本）为最小。它是一个高维数、非线性、多约束的混合整数规划问题。当系统的规模扩大时，尤其是计及可再生能源后，传统优化算法已很难从理论上求得最优解，如备用准则法、随机优化法、混合整数规划法、鲁棒优化法等，这些算法往往存在“维数灾”和计算精度差的特点，难以考虑大量的约束条件和解决多目标优化问题[2]。因此面对这类问题时，现代智能优化算法在运算速度和精度上都体现出了极大的优越性。但到目前为止，仍不存在一种既能全面考虑各种约束条件，又能获得比较理想的运算速度和精度的实用算法。因此，不断改进和探索新的求解算法对电力系统的经济运行具有重要的意义。

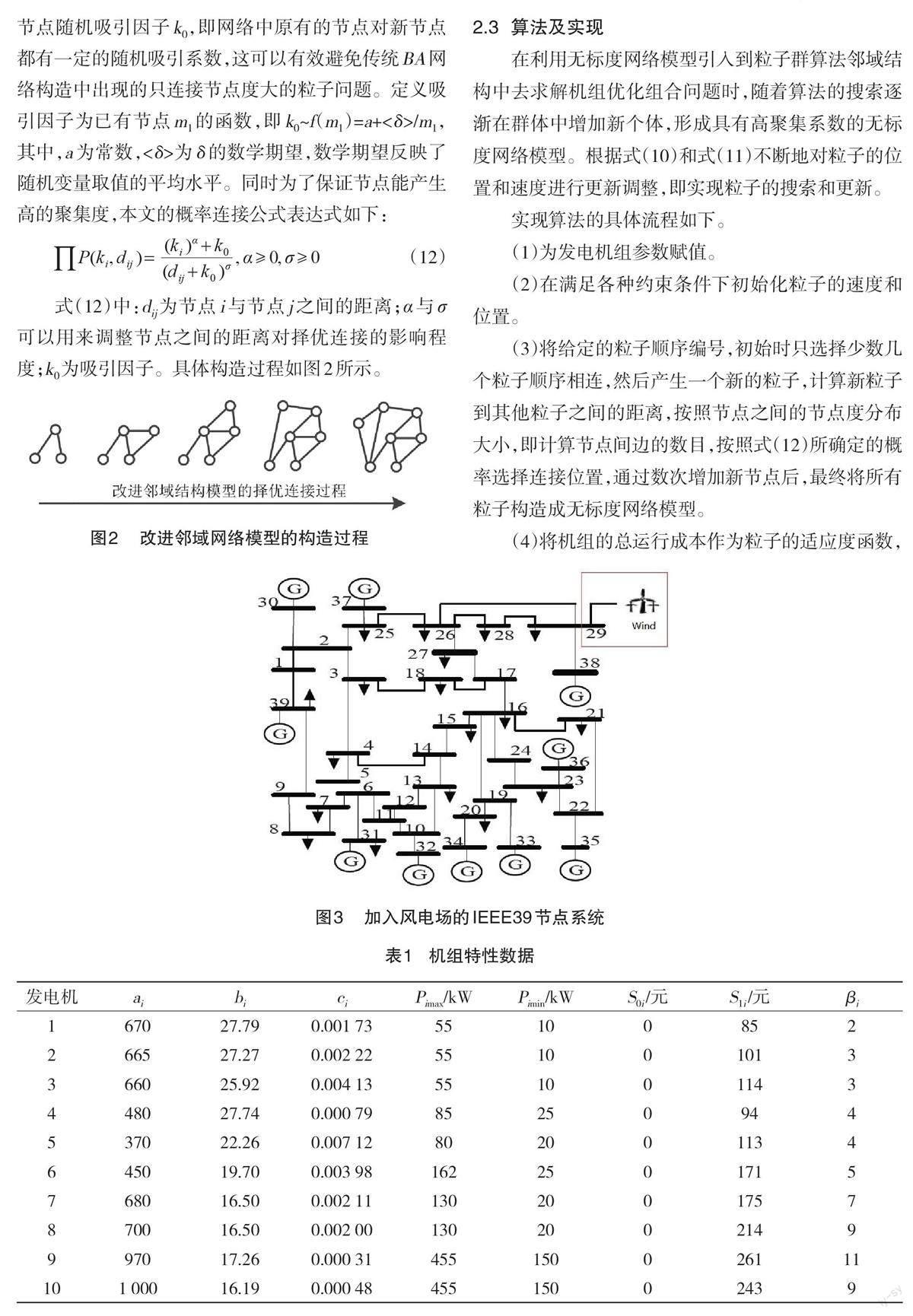
基于上述背景，本文在基本粒子群算法的基础上，改进了无标度网络生成过程中的择优与增长连接机制，提出了一种基于高聚集度的无标度网络邻域结构的粒子群算法，并采用条件风险价值对风电不确定性带来的风险损失进行了描述。通过建立以发电成本和弃风成本最小为目标函数的数学模型，并根据修改的IEEE39 节点系统对所提模型和算法的正确性和有效性进行了验证。

1 风险模型与数学模型描述

1.1 风险价值模型

随着风电接入容量的增多，系统有功功率失衡引起的失负荷与弃风风险概率随之增大[3]，为了有效降低发生事故带来的高损失，本文采用了风险价值管理模型，以S（e_t^w）表示t 时刻失负荷损失函数。