电池储能系统充放电控制策略仿真研究

禹淼源, 陈 燕, 窦银科, 秦金涛, 毛轻扬

(太原理工大学 电气与动力工程学院, 山西 太原 030024)

随着环境问题的愈发突出和传统化石能源的日渐短缺,全球范围内都在加快对新型绿色能源的开发与利用。其中较为典型的新型能源,如风能、太阳能等,在利用方面受到气象条件的制约,呈现出随机性与波动性等特点,对新能源发电系统的稳定运行造成不利影响[1]。在新能源发电系统中,部署电池储能系统可以平抑新能源带来的波动,提高能源利用率,提升整个电力系统运行的经济性和可靠性[2]。对储能电池充放电过程进行良好的控制既可以延长储能电池的使用寿命,又可以提高系统运行的安全性和稳定性。因此,研究储能电池充放电过程的特性、控制算法等显得尤为重要。对储能电池充放电控制的研究是能源领域当下热门的研究方向之一,其中对充放电控制的研究主要集中在最大充放电功率的控制、充放电策略的优化、充放电优先级的控制以及电池荷电状态的管理等方面。

针对储能电池充放电过程中的控制问题,本文搭建了电池储能系统的整体电气模型,以双向半桥DC/DC变换器为能量传输通道,在储能电池充放电过程中采用以PI控制为基础的双闭环控制,以保证控制过程的动态响应速度快和良好的控制性能。

1 电池储能系统结构

利用双向半桥DC/DC变换器可以实现对电源端以及电池端的充放电控制,在控制算法合理有效的情况下,可以提高系统整体的能量利用率。双向DC/DC变换器可分为含变压器的隔离型和不含变压器的非隔离型。隔离型由于引入了变压器,可以实现输入与输出端的电气隔离,并可以实现多级输出,使运行方式变得更加丰富灵活[3]。但由于变压器的存在,亦使得系统的整体结构与控制方式变得更加复杂,故对于小型的储能系统,多选用不含变压器的非隔离型。

电池储能系统结构如图1所示,主要的电路元件为电容、电感和绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor,IGBT)。

图1 电池储能系统结构

图1中,U1为电源电压,U2为电池端电压,V1、V2为IGBT。图1所示的电路可分别工作于Buck/Boost模式:当V2作为主功率管、V1停止工作时,电路工作于Buck模式,此时电池处于充电状态;当V1作为主功率管、V2停止工作时,电路工作于Boost模式,此时电池为放电状态[4]。

本文所搭建的双向半桥DC/DC变换器电路如图2所示,由储能电池、双向半桥DC/DC变换器和控制系统组成,储能电池以双向半桥DC/DC变换器为能量传输通道。

图2 双向半桥DC/DC变换器电路

图2中,S1、S2分别为双向半桥DC/DC变换器中IGBT的脉冲宽度调制(Pulse Width Modulation,PWM)脉冲信号输入。在储能电池充放电过程中采用以PI控制为基础的双闭环控制,控制系统对储能系统运行过程中相关参数进行采集之后,将直流侧输出电压与参考电压进行比较,根据比较的结果决定对哪一个开关器件施加触发脉冲,从而决定储能电池是处于充电或放电状态,与此同时,通过对储能电池充放电过程的控制,来维持直流侧电压的恒定。

2 双闭环控制原理

目前,各种类型的控制方法不断涌现,但PID控制仍作为主要的控制方法被广泛应用于工程实践当中。PID控制的参数调试方法成熟且简单,根据经典的调试方法得到的参数即可起到优秀的控制效果,且在实际应用中仅需要少量的代码就可以完成对PID控制器的编程[5]。尽管PID控制器存在着诸多优点,但在电机调速控制以及电力电子技术领域,为避免微分环节可能导致的高频振荡,更多的还是采用PI控制,PI控制的校正环节更容易进行建模,并且省去了微分项参数的调试整定,实现起来将更为方便[6]。其表达式为

(1)

式中:KP——比例增益系数;

KI——积分增益系数;

τ——积分时间常数;

s——微分因子。

为实现对储能电池充放电过程良好、快速控制,本文所采用的双闭环控制框图如图3所示。控制流程分别采用了电压环与电流环双闭环控制,并且在电压环与电流环的双闭环控制过程中,均采用了PI调节器[7]。对于电压环的控制而言,将输入电压与参考电压进行比较,将比较结果作为PI调节器的输入,其目的是当系统受到扰动时,可以稳定输出电压;对于电流环的控制而言,使输入电流对参考电流进行追踪,其目的是提高系统动态响应速度。

图3 双闭环控制框图

图3中,U1ref、iLref分别为参考电压与参考电流;U1为储能电池的端电压;iL为储能电池的输出电流;UN为馈电压;d为占空比;Gid(s)、Z(s)分别为电流环和电压环的开环传递函数。

3 系统仿真建模

为了验证本文所提出的控制算法对电池储能系统充放电过程中的控制性能,在MATLAB/Simulink中,以双向半桥DC/DC电路为桥梁,搭建电池储能系统的整体电气模型,并对模型进行仿真实验。

3.1 储能电池模块的建模与参数设置

储能电池模块选择Simulink元件库中自带的“Battey”模型,电池的类型选择锂电池,对电池的标称电压、额定容量、初始的荷电状态以及响应时间等参数进行合理的设置,其他参数则采用系统默认值,具体的参数设置如表1所示。

表1 储能电池模块参数设置

3.2 双向半桥DC/DC变换器的建模与参数设置

根据DC/DC变换器的电路原理图在Simulink中搭建电池与其相连接的仿真模型。为了后续储能系统整体的管理与调试,对所搭建的模型采取子系统封装的措施,具体如图4所示。图4(b)中,ISC与SOC分别为电池电流与电池的荷电状态。

图4 储能电池与双向半桥 DC/DC 变换器连接模型

3.3 双闭环控制的仿真建模

根据图3所示的控制框图,在Simulink中搭建相应的仿真模型,为便于后续的调试与管理,同样对双闭环控制仿真模型进行子系统封装,具体如图5所示。

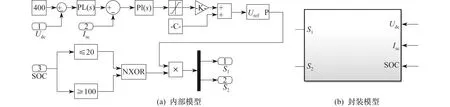
图5 双闭环控制仿真模型

考虑到电池可能存在过充或过放的问题,当电池的SOC≥100%或者≤20%时,控制算法将会对PWM控制信号进行闭锁,使双向DC/DC变换器停止工作。在封装模型图5(b)中,Udc为直流母线电压。

3.4 电池储能系统整体的仿真建模

为模拟电池的充放电过程,仿真所采用的负载模型既要具备负载特性来消耗电池的电能,又要具备电源特性来对电池进行充电。为实现这个功能,本文采用Simulink元件库中的受控电压源元件与电阻串联作为系统的负载,当受控电压源的输入为正时,其代表充电电源;输入为负时,其代表放电电源。将负载模型与上文封装的两个子系统进行连接,得到的电池储能系统的整体仿真模型如图6所示。

图6 电池储能系统整体仿真模型

此外,为达到较好的控制效果,通过多次的仿真实验,从系统整体的仿真速度、仿真精度等方面比较之后,最终所采用的仿真算法为ODE23TB。

4 仿真结果分析

根据上述的系统整体仿真模型,对所提出的控制算法的可行性与有效性进行实验验证。根据文献[8]的推导和仿真实验过程中的调试,设计电压环PI控制器参数KP为0.55、KI为13;设计电流环PI控制器参数KP为1.2、KI为25。为模拟电池的充放电过程,使受控电压源与电阻串联的部分在0～1.2 s时为负载性质,消耗电能,其中在0.4 s时增大负载;在1.2～2 s时为电源性质,为电池充电。

电池端电压的仿真波形与电池荷电状态的仿真波形如图7所示。在0～1.2 s时,电池端电压逐渐减小的同时,电池荷电状态在下降,表示电池正在进行放电;在1.2～2 s时,电池端电压逐渐增加的同时,电池荷电状态在上升,表示电池正在进行充电。实验结果与理论设定相一致,验证了所搭建仿真模型的正确性。

图7 模型正确性验证仿真波形

直流母线电压和电池电流的仿真波形如图8所示。

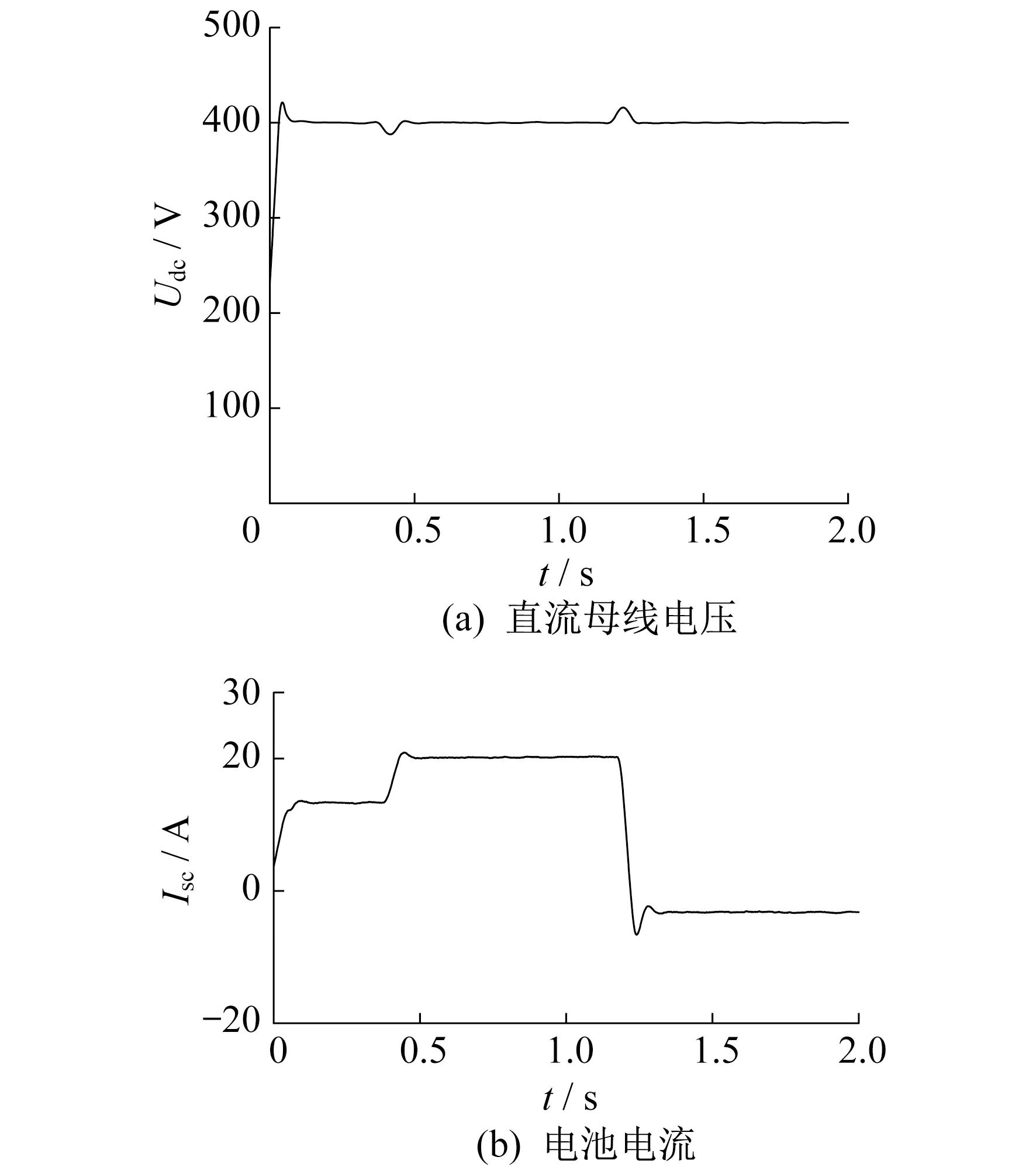
图8 控制算法性能验证仿真波形

由图8(a)可知,当负载发生变化时,直流母线电压经过小幅度的波动后能够迅速恢复至稳定值,全程基本保持在400 V。图8(b)中电流大于零的部分表示电池处于放电状态,电流小于零的部分表示电池处于充电状态。由图8(b)可以看到,当外界发生变化时,系统所采用的双闭环控制能够迅速做出反应,使电池的输出电流趋于稳定。实验仿真结果验证了所提出的控制算法的正确性与可行性。该算法跟踪速度快、稳态精度高,保证了电池充放电控制过程的快速性与稳定性。

5 结 论

(1) 电池端电压与电池荷电状态的仿真波形变化与理论设定相一致,验证了本文所构建模型的正确性。

(2) 仿真实验结果表明,当负载发生变化时,电池储能系统相关参数经过短暂波动后能迅速恢复至稳定值,表明了本文所提出的控制算法动态响应速度快、控制性能好。

(3) 本文所采用的控制策略能够满足储能电池充放电过程中对控制系统性能的需求。