基于K-Means聚类与灰色关联分析对玻璃文物成分的研究

徐 惠，胡 珊，姚旭敏，储昭顺

（安徽财经大学统计与应用数学学院，安徽 蚌埠 233030）

针对古代玻璃制品的成分分析与鉴别，李青会等人于2006年对战国时期的玻璃珠进行研究，利用现代技术，得出战国时期中国境内同时存在三种硅酸盐玻璃，中国古代的PbO、BaO、SiO2和K2O、SiO2玻璃在技术发展上应该具有密切联系的结论［1］；又于2007年利用相关技术对中国古代玻璃的化学成分进行分析，指出应加强对西周到战国时期中国出土的釉砂、玻砂、镶嵌玻璃珠，以及伴随古代玻璃同时出土的绿松石等文物的科技研究［2］。

对于近代玻璃的研究，赵娟等人于2002年在相关组分制造硒硫化镉颜色玻璃中的作用研究中，指出在制造硒硫化镉颜色玻璃时，除了加入玻璃的基本组成SiO2和着色剂CdS、Se 外，还必须加入ZnO、碱金属氧化物、冰晶石、B2O3和重金属硫化物等次要组分［3］；王承遇等人于2003年综述了影响浮法玻璃等的耐风化性因素，风化产物的形貌和风化过程，得出了玻璃表面风化析碱量随风化温度、湿度和时间而增加的结论［4］。

文章针对古代玻璃制品的研究，借鉴近代玻璃的研究成果，立足于新的数据，从成分分析与鉴别方面进行研究，拟运用K-均值聚类、灰色关联分析、BP神经网络等方法建立模型，研究高钾类型与铅钡类型玻璃的分类依据，以及两类玻璃文物风化的难易程度。

1 数据来源和假设

文章数据来源于2022年全国大学生数学建模竞赛。为便于解决问题，研究过程和结论均建立在以下假设成立的基础上：（1）颜色空白数据的划分整合对关系判断无影响；（2）剔除风化玻璃选出未风化（未风化玻璃选出风化）数据对结论无影响；（3）含量预测时单一变量预测不会影响最终预测结果；（4）预测值不真实，为考虑真实性，使用原始数据进行BP神经网络模型对化学成分分析无影响。

2 基于随机森林插补的K-Means聚类分析模型

2.1 随机森林插补法数据处理

根据玻璃制品的相关数据，分析表面风化与其他三个变量的关系，比较其出现频率，进行四个变量之间的卡方检验，分析变量之间的差异性。研究玻璃文物表面有无风化以及其化学成分含量的统计规律。首先，根据表单数据将玻璃类型分为高钾和铅钡类，控制变量分析其他数据，改变前几个变量，分析元素的平均值，多个控制变量比较分析。其次，使用缺失森林插补法进行模拟预测，预测风化前化学成分含量［5］，发现未风化的高钾与铅钡玻璃数量相同，而风化的高钾玻璃明显少于铅钡玻璃；所以高钾类型玻璃相对较难风化，铅钡类型玻璃相对易于风化。对所有数据按照风化、无风化进行划分，统计不同类型、纹饰、颜色的成分总含量。对类型、纹饰与表面风化进行分类，计算均值，发现SnO2只存在于铅钡风化纹饰C 中，无风化玻璃中含量较多的都是活泼型较低的成分（K2O 除外），含量相似玻璃中铅钡纹饰A 和C 所含的氧化物种类与数量大致相同；高钾纹饰B 型不含有的氧化物（等于0）较多，说明在风化过程中高钾玻璃与环境元素交换时，交换的元素较少，较稳定。高钾玻璃在风化后的主要化学成分含量减少；铅钡玻璃在风化后主要化学成分含量增加（SiO2的含量变化相反）。最后，将总体数据分为高钾和铅钡类型，视高钾和铅钡风化时期的数据为缺失，根据随机森林算法对缺失值进行填充，得到补充完整的数据。利用补充的高钾和铅钡风化数据预测未风化的数据。

2.2 K-Means聚类研究

分析高钾和铅钡玻璃的分类规律，使用K-Means分析方法显现分类标准。对高钾和铅钡玻璃亚类进行划分，建立了分层聚类模型。检查两类数据的缺失值情况，初步判断聚类的可信率；根据聚类树状图进行分析，对聚类情况和数据进行探测，进行亚类划分。

依据单因素方差进行合理性分析，分析高钾与铅钡类的氧化物，将标准差较大数值的氧化物与亚分类的氧化物进行比较，观察是否都存在；改变其中一项氧化物的数值重新分层聚类，划分亚类与之前的比较，若改变数值的氧化物不出现在亚类中，说明检验的敏感性。

分析表单数据，确定类别1为高钾，类别2为铅钡；对数据进行K-Means聚类分析，得到字段差异分析和聚类中心点坐标，以聚类1 的中心点坐标作为横坐标，建立成分中心散点图，如图1所示。总体与y=x进行对比，形成成分比较分析散点图，取出与y=x的斜率相差较大的点进行分析。

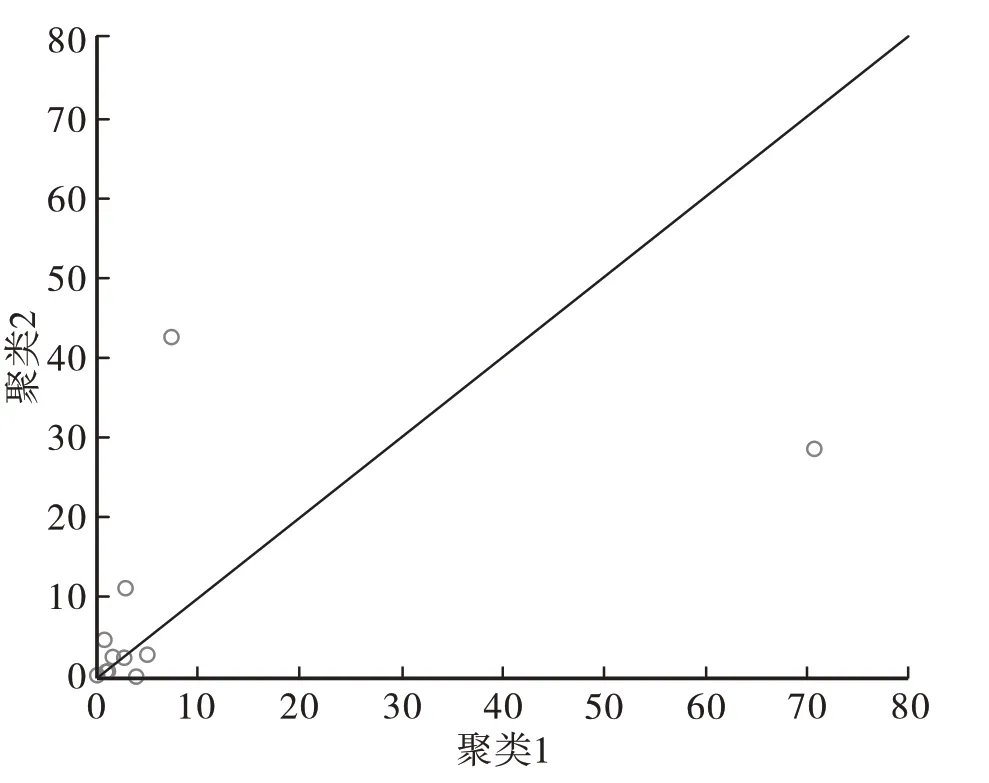
图1 成分中心散点图

利用单因素方差分析得出分析图，如图2所示。分析含量较大的成分，二氧化硅（SiO2）、氧化钾（K2O）的含量在高钾类含量较多，氧化铅（PbO）、氧化钡（BaO）在铅钡中含量较多。这四种氧化物的标准差较大，数据较为分散。

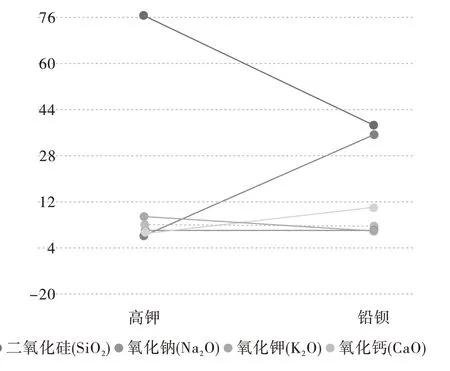
图2 单因素方差分析图

2.3 分层聚类分析

采用欧氏距离作为指标，对关联度较大的前k种气象因素进行分层K-Means 聚类（k的值取决于样本的多少以及精度的需求），聚类完成后得到多个化学成分样本子集。在确定了该相似性距离为聚类指标后，采用结合欧氏距离和ρ(X,Y)为标准的多重聚类方法［6］。

在X和Y归一化之后，其之间的协方差ρ(X,Y)表示为

建立分层聚类模型为

其中，yi代表在一系列观测变量中的个体值，K代表群的个数，πk表示一个个体值属于k群（或k群的大小）的先验概率，θ表示模型的参数，f(yi|θ)是指当特定集群的混合密度θ作为模型参数时，yi的分布情况。

同样地，弗莱利和拉夫特里提出可以将上式中的模型表现为下述的相似形式：

其中，f(yi|θ)符合多元正态（高斯）分布φk，参数包括平均值μk和方差矩阵∑k.

总体数据分为高钾和铅钡类型，分别运用Matlab 对其进行分层聚类；检查数据的缺失值情况，初步判断聚类的可信率；根据聚类表了解样本之间的距离和聚类情况；高钾和铅钡类型的聚类树状图如图3 所示，分析聚类树状图，对聚类情况和数据进行探测，发现各类之间的层次关系，对数据进行亚类划分。

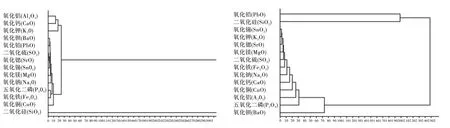
图3 高钾（左）和铅钡（右）类型的聚类树状图

根据聚类系数与树状图进行亚类划分，高钾类型：高钾主要分为二氧化硅（SiO2）与类别1，类别1分为氧化铜（CuO）与类别2，类别2 分为氧化钾（K2O）与类别3，类别3 分为氧化钙（CaO）与氧化铝（Al2O3）。铅钡类型：铅钡主要分为二氧化硅（SiO2）、氧化铅（PbO）与类别1，类别1分为氧化钡（BaO）与类别2，类别2分为氧化铝（Al2O3）与类别3，类别3分为氧化铜（CuO）与氧化钙（CaO）。

2.4 基于单因素方差分析的模型检验

将分类数据进行单因素方差分析，得到方差齐性检验，如表1所示。观测变量标准差，如果标准差较大，说明观测变量的变动主要是由控制变量引起的，可以主要对观测变量进行解释，控制变量给观测变量带来了显著影响，即控制变量对于观测变量具有敏感性。

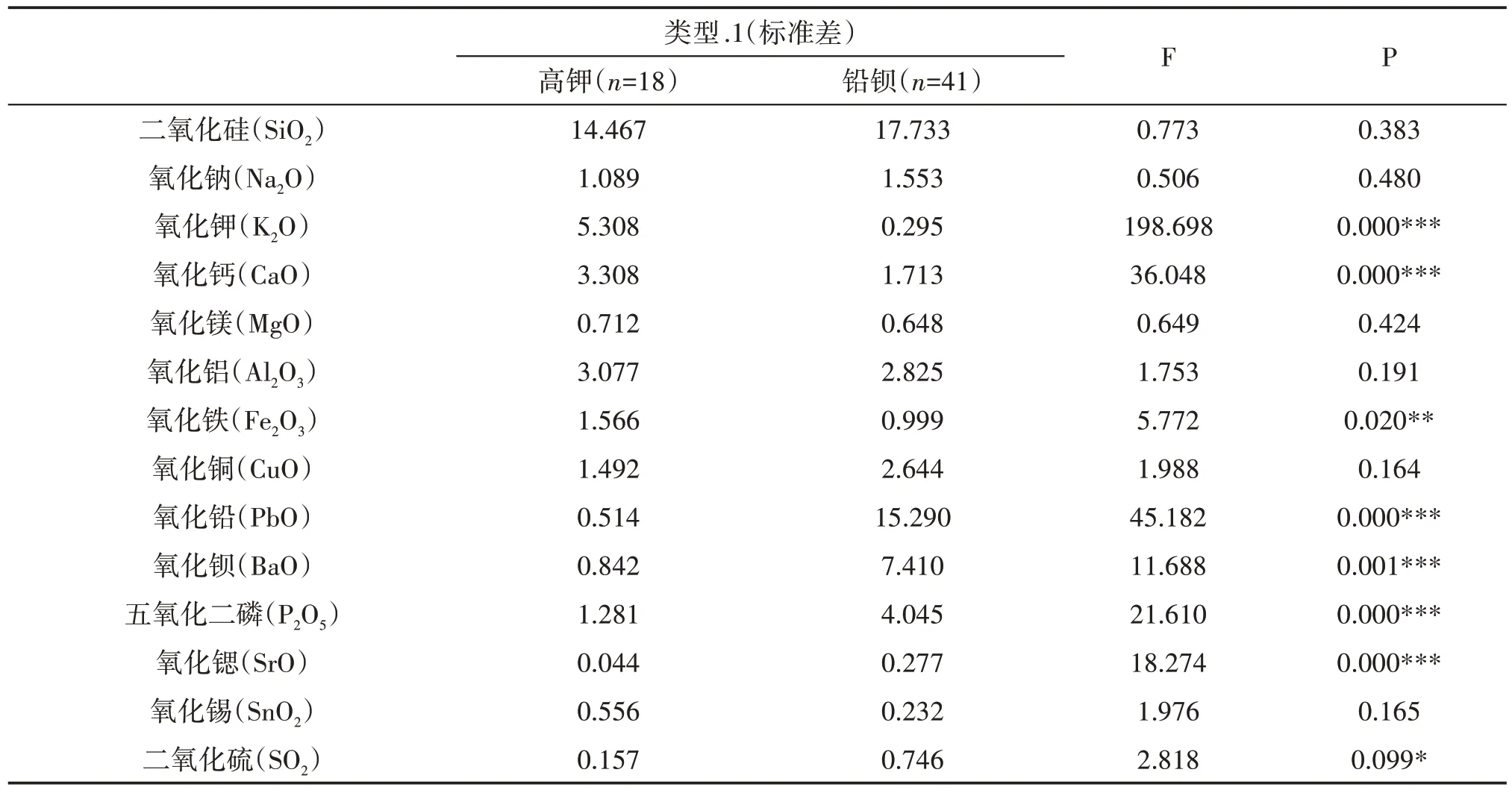
表1 方差齐性检验

由表1 可知，高钾类标准差较大的有二氧化硅（SiO2）、氧化钾（K2O）、氧化钙（CaO）、氧化铝（Al2O3）、氧化铁（Fe2O3），相对于高钾分类主要结果多出氧化铁（Fe2O3）；铅钡类标准差较大的有二氧化硅（SiO2）、氧化钙（CaO）、氧化铝（Al2O3）、氧化铜（CuO）、氧化铅（PbO）、氧化钡（BaO）、五氧化二磷（P2O5），相对于铅钡分类主要结果多出五氧化二磷（P2O5），但所有分类结果都完整，展示出分类结果的合理性。

3 基于主成分分析的玻璃文物成分分析

3.1 研究思路

为便于分析，将数据表单分为风化与未风化两个部分，通过主成分分析提取主成分，得出所有主成分贡献率均小于30%，除第一主成分大于20%外，其余主成分均小于20%，剔除其他成分形成数据表，利用BP 神经网络模型进行二次鉴别；在BP 神经网络模型中，去除变量氧化钠的影响，研究其他变量的特征，得到鉴别玻璃类别结果。

3.2 研究方法

3.2.1 主成分分析模型

对表单三数据进行主成分分析，提取主成分。使用主成分分析法计算各个主成分的贡献率，得到特征值、贡献率和累计贡献率，得出所有主成分贡献率均小于30%，除第一主成分大于20%外，其余主成分均小于20%，如表2所示。

重点研究第一主成分各个变量的特征向量。通过对第一主成分表达式的分析，可以得出氧化钠变量的系数，相较于其他变量，小于1个数量级；同时氧化钠的数值大多数为空，故剔除变量氧化钠的数据。

3.2.2 BP神经网络模型

在BP 神经网络中，相邻层的神经元进行全连接，每层各个神经元之间无连接，网络按照有监督方式学习，当一对学习模式提供网络后，各神经元获得网络的输入响应产生连接权值。然后按减少希望输出与实际输出误差的方向，从输出层经各中间层逐层修正各连接权值，回到输入层［7］。

在BP神经网络模型中，基于Python去除变量氧化钠的影响［8］，研究其他变量的特征，从而达到鉴别玻璃类别的目的。为便于推断玻璃类别，将数据分为风化、未风化两个部分数据，分别进行BP 神经网络模型检验；得到鉴别结果，其中A1、A6、A7为高钾玻璃，A2、A3、A4、A5、A8为铅钡玻璃。

3.3 模型检验

对于表中数据运用SPSS 进行量化分析，分别判断样本所属大类（类别1：高钾；类别2：铅钡），得到效应量化分析表，如表3所示。进而对不同氧化物类别进行单因素方差分析，用于检验高钾和铅钡类别数据是否存在显著性差异。

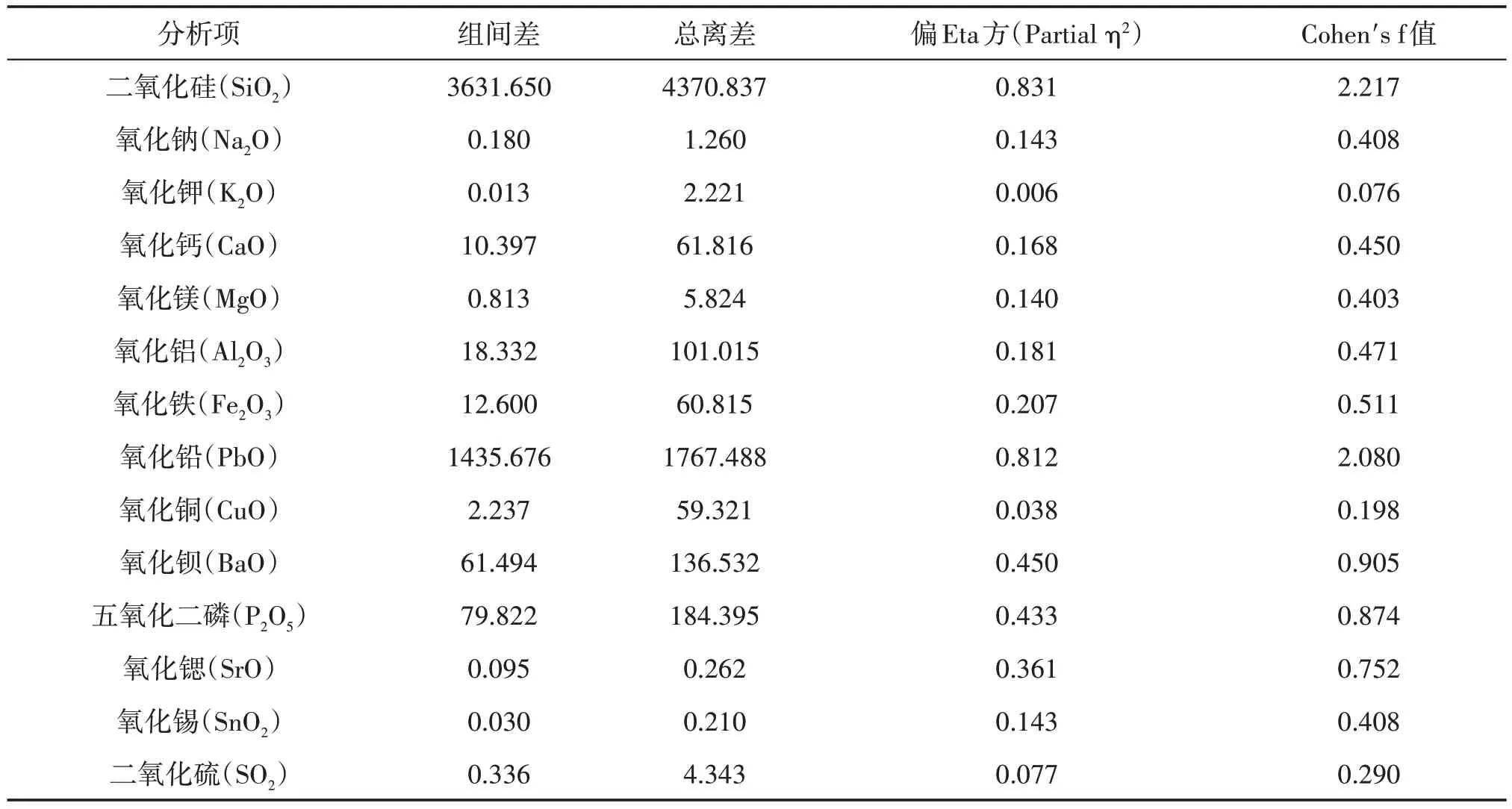
表3 效应量化分析表

效应量化分析的结果显示，基于二氧化硅（SiO2）、氧化钠（Na2O）、氧化钙（CaO）、氧化镁（MgO）、氧化铝（Al2O3）、氧化铁（Fe2O3）、氧化铅（PbO）、氧化钡（BaO）、五氧化二磷（P2O5）、氧化锶（SrO）、氧化锡（SnO2），对于Eta方（η²值）较大，数据的差异来源于不同组别间的差异；Cohen´s f值较大，即数据的效应量化的差异程度为大程度差异，分析效应量化数据Eta方（η²值），与Cohen´s f值，对于分类结果氧化物的敏感程度较高。

4 灰色关联分析模型

4.1 研究思路

通过建立灰色关联度模型，代入亚类划分出的高钾和铅钡3个类别中的氧化物数值，进行灰色关联性分析，得到氧化物与高钾、铅钡之间的关联度；然后对两种类型的化学成分进行多配对样本Friedman 检验，具有显著性的使用Friedman 检验，不具有显著性的使用正态性检验直方图，得到氧化物之间的关联与差异幅度；最后进行灰色关联分析，得到氧化物之间的灰色系数表，分析高钾与铅钡类型中氧化物之间的线性与非线性关系。对得到的关联关系进行高钾类型与铅钡类型的比较，得出差异性。

4.2 研究方法

4.2.1 灰色关联分析模型

针对数据进行无量纲化处理（均值化、初值化），求解母序列（对比序列）和特征序列之间的灰色关联系数值和灰色关联度值，对灰色关联度值进行排序，得出结论，即设系统特征行为序列为

系统的相关因素行为序列为

记折线

为(Xi)°

令

则灰色绝对关联度为

计算关联系数为

则关联度为

灰色系统理论着重考虑点点之间的距离远近对关联度的影响。其中，ρ称为分辨系数，一般情况下，取ρ= 0.5.对于ρ取值的一般原则，避免了系统因子观测序列的异常值支配整个系统关联度取值的情况，能够使关联度更好地体现系统的整体性［9］。根据观测值动态变化选取分辨系数ρ的值，使其取值具有一定的客观基础，具体取值规律如下：

记∇v为所有差值绝对值的均值，即

记ε∇=，则ρ的取值为

当∇max > 3∇v时，ε∇≤ρ≤1.5ε∇；

当∇max ≤3∇v时，1.5ε∇≤ρ≤2ε∇.

注：分辨系数ρ∈（0，∞），ρ越小，分辨力越大，一般ρ的取值区间为（0，1），具体取值可视情况而定。当ρ≤0.5463时，分辨力最好，通常取ρ=0.5.

关联度表示各评价项与“参考值”（母序列）之间的相似关联程度，其是由关联系数进行计算平均值得出，关联度值介于0～1之间，该值越大表示评价项与“参考值”（母序列）相关性越强，关联度越高，意味着评价项与“参考值”（母序列）之间关系越紧密，因而其评价越高。结合关联度值，针对所有评价项进行排序，得到各评价项排名［10］。

结合上述关联系数结果进行加权处理，最终得出关联度值，使用关联度值针对14 个评价对象进行评价排序，如表4所示。

表4 灰色关联度分析

从高钾关联度表可以看出：针对高钾类别内部氧化物本次5个评价项，分析可得评价氧化铅（PbO）最高（关联度为：0.807），其次是二氧化硅（SiO2）（关联度为：0.614）；从铅钡关联度表可以看出：针对铅钡类别内部氧化物本次6 个评价项，分析可得二氧化硅（SiO2）评价最高（关联度为：0.868），其次是氧化铝（Al2O3）（关联度为：0.860）。

4.2.2 多配对样本Friedman检验模型

高钾类型二氧化硅（SiO2）、氧化钾（K2O）、氧化钙（CaO）显著性P 值<0.05，水平上呈现显著性，拒绝原假设，因此数据不满足正态分布，可以进行Friedman 检验［11］，如表5 所示。氧化铝（Al2O3）、氧化铜（CuO）显著性P值>0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足正态分布，建议采用方差分析［12］。

表5 高钾Friedman检验分析结果表

通过分析可知，显著性P 值为0.000***，因此统计结果显著，说明二氧化硅（SiO2）、氧化钾（K2O）、氧化钙（CaO）之间存在显著差异；其差异幅度Cohen´s f值为：4.13，差异幅度非常大。

铅钡类型二氧化硅（SiO2）、氧化钙（CaO）、氧化铝（Al2O3）、氧化铜（CuO）、氧化钡（BaO）显著性P值<0.05，水平上呈现显著性，拒绝原假设，因此数据不满足正态分布，可以进行Friedman 检验，如表6 所示。氧化铅（PbO）显著性P值>0.05，水平上不呈现显著性，不能拒绝原假设，因此数据满足正态分布，建议采用方差分析。

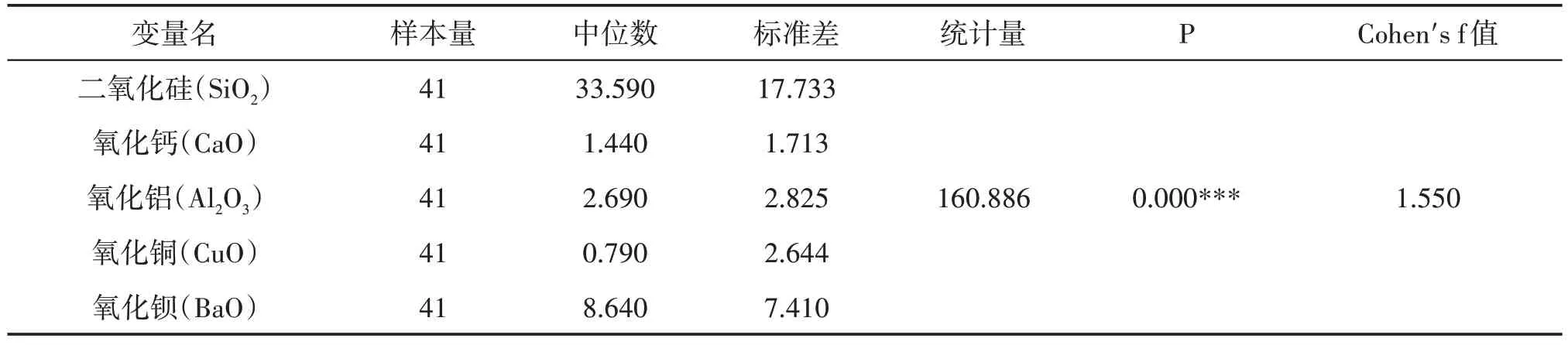
表6 铅钡Friedman检验分析结果表

显著性P值为0.000***，因此统计结果显著，说明二氧化硅（SiO2）、氧化钙（CaO）、氧化铝（Al2O3）、氧化铜（CuO）、氧化钡（BaO）之间存在显著差异；其差异幅度Cohen´s f值为：1.55，差异幅度较大。

铅钡类型氧化铅（PbO）正态图基本上呈现中型，数据基本可接受为正态，所以与其他化学成分之间差异性较小。

4.2.3 结果分析

根据高钾玻璃和铅钡玻璃亚类划分后的氧化物数据，进行灰色关联度相关性分析，得到高钾和铅钡相关系数，如表7所示。

表7 高钾和铅钡相关系数

根据高钾关联度相关性分析，得到氧化物二氧化硅（SiO2）与氧化钾（K2O）、氧化钙（CaO）、氧化铝（Al2O3）、氧化铜（CuO）呈负指数相关；氧化物氧化钾（K2O）与氧化钙（CaO）、氧化铝（Al2O3）、氧化铜（CuO）呈正指数相关；氧化物氧化钙（CaO）与氧化铝（Al2O3）、氧化铜（CuO）呈正指数相关；氧化物氧化铝（Al2O3）与氧化铜（CuO）呈正指数相关。

根据铅钡关联度相关性分析，得到氧化物二氧化硅（SiO2）与氧化钙（CaO）、氧化铅（PbO）、氧化钡（BaO）、氧化铜（CuO）呈负指数相关，与氧化铝（Al2O3）呈正指数相关；氧化物氧化钙（CaO）与氧化钡（BaO）、氧化铜（CuO）呈负指数相关，与氧化铝（Al2O3）、氧化铅（PbO）呈正指数相关；氧化物氧化铝（Al2O3）与氧化铅（PbO）、氧化钡（BaO）、氧化铜（CuO）呈负指数相关；氧化物氧化铅（PbO）与氧化钡（BaO）、氧化铜（CuO）呈负指数相关；氧化物氧化钡（BaO）与氧化铜（CuO）呈正指数相关。

5 结论

通过分析得到高钾与铅钡的灰色关联度，进行相关性分析得到各类氧化物的正负相关指数，分析得到高钾与铅钡大类的氧化物之间正负相关指数交替出现。对于高钾玻璃类别氧化物正相关指数偏多，一类氧化物往往会带动另类氧化物的同向含量变化，氧化物总体呈现方骖并路趋势；对于铅钡玻璃类别氧化物负指数相关偏多，一类氧化物往往会带动另类氧化物的异向含量变化，氧化物总体呈现此消彼长趋势。