基于样本可靠性的时空正则化自适应相关滤波目标跟踪

陈中意,陶 洋

(重庆邮电大学 通信与信息工程学院,重庆 400065)

1 引 言

目标跟踪是计算机视觉领域中一个基础性问题,在无人驾驶、人机交互、视频监控等领域具有广泛的应用[1].目标跟踪的任务是通过给定第1帧的初始化边界框来估计目标物在下一帧的边界框[2].一般来说,影响目标跟踪性能的问题有很多,如快速运动、旋转、物体遮挡、光照变化以及图像分辨率低等挑战.近十几年来,目标跟踪算法的研究不断深入,出现了大量优秀的算法,目标跟踪的性能得到了显著的提升,面临的困难也得到了进一步的解决,但实现一种在复杂场景下跟踪准确、快速和稳健的目标跟踪算法依然是一项艰巨的任务[3].

基于相关滤波的目标跟踪算法借助循环矩阵和频域计算与传统方法相比,其性能更好、速度更快,得到广泛应用.但循环位移会导致边界效应,引入背景杂波而导致模型学习到错误样本降低模型的准确性.在2010年,Bolme[4]等提出了平方误差最小输出相关滤波器(MOSSE),MOSSE相关滤波器首次将相关滤波引入到目标跟踪领域,在各大主流数据集上表现优秀,研究基于相关滤波的目标跟踪算法的潮流开始兴起.Henriques[5]等提出了循环核相关滤波算法(CSK),该算法是基于MOSSE进行改进的,引入核函数和循环密集采样提高目标跟踪算法的稳健性,但CSK利用的仅是样本的灰度特征,对目标的外观特征表达能力较弱.Danelljan[6]等提出了核相关滤波算法(KCF),为增强跟踪模型的目标特征表达能力,使用具有31个通道的方向梯度直方图(HOG)特征替代原来单一通道的灰度特征.为缓解边界效应,Danelljan[7]等提出了一种基于空间正则项的相关滤波目标跟踪(SRDCF)算法,该算法引入空间权重矩阵对滤波器进行抑制,对远离目标中心的特征抑制较强,能较好的解决边界效应问题,但引入空间权重矩阵以后,目标函数的封闭解被破坏,跟踪速度只能达到4 frame/s,同时其预设的是固定的负高斯形状的空间权重矩阵,在快速运动、遮挡等场景下,无法自适应目标的变化,导致跟踪漂移.Galoogahi等人[8]提出了基于背景感知的相关滤波跟踪(BACF)算法,为获取真实的负样本,对其搜索的范围进行扩张,同时对样本进行循环位移采样,增加样本数量,提高了模型对于背景和目标的辨别能力.但较大的搜索范围会引入较多的背景杂波,容易造成跟踪漂移.Huang等人[9]在BACF的基础上提出了基于异常响应抑制的相关滤波(ARCF)跟踪算法,其利用前后两帧响应图的全局变化情况检测跟踪过程中的异常情况,避免滤波器错误学习过多的背景信息,能有效的解决边界效应以及抑制畸变.Li等人[10]以SRDCF为基础,提出了基于时空正则化的相关滤波目标跟踪(STRCF)算法,将前后两帧滤波器的信息充分利用,避免跟踪模型发生退化.但时间正则项的超参数是一个固定值,在跟踪的过程中对时间正则项的惩罚力度固定,在发生相似背景干扰的时候无法自适应增强对时间正则项的约束,容易导致跟踪漂移.

以上方法虽然在一定程度上减轻了边界效应对目标跟踪的影响,但还是存在诸多问题.本文在STRCF算法的基础上提出一种基于样本可靠性的时空正则化自适应相关滤波目标跟踪算法,该算法通过样本可靠性构建空间参考权重矩阵,利用自适应空间正则项缓解边界效应,同时使用前后两帧响应图的全局变化程度确定时间正则项的超参数,适应复杂背景防止模型发生突变,缓解跟踪漂移.

2 时空正则化相关滤波算法

基于相关滤波的跟踪算法借鉴了信号处理当中互相关的思想[11],提出了模板匹配的跟踪方法,其将目标与搜索区域进行相关性匹配,其中匹配度最高的区域即为目标预测结果.

基于时空正则化相关滤波(STRCF)目标跟踪算法以相关滤波理论为基础,提取目标的多维特征,通过循环位移矩阵增加样本数量,采用岭回归的思想训练相关滤波器,引入了空间正则项与时间正则项,能够有效降低边界效应的影响,提升基于相关滤波目标跟踪算法的性能与鲁棒性.STRCF算法的目标函数如下:

(1)

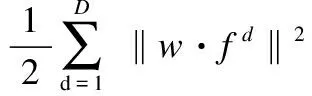
由STRCF算法的目标函数可知,其在目标函数中引入了固定的空间权重矩阵,减少了边界效应的影响.但在目标形变、遮挡、旋转等场景下,空间权重矩阵不能自适应目标的外观变化,无法获取可信任的空间权重矩阵,容易导致跟踪漂移.空间权重矩阵应是动态的,与目标的变化建立相关的联系,使得滤波器可较好避免学习到背景信息,提升模型对目标和背景的辨别能力.STRCF算法为防止滤波器突变,引入了时间正则项.其固定的时间正则项超参数,使得对每一帧的滤波器进行了相同的抑制,在一定程度上避免了滤波器的突变,但无法适应一些复杂的目标跟踪场景.

3 本文算法

3.1 空间可靠性

在STRCF算法中引入空间正则项在一定程度上减轻了边界效应对目标跟踪模型的影响,但在跟踪的过程中其空间权重矩阵是固定的,空间权重矩阵未与目标物建立联系,对于不同场景下的目标惩罚约束力度相同不免会惩罚有效样本,在后续目标跟踪过程中无法自适应更新.故本文提出基于样本可靠性的自适应空间正则项,建立与目标之间的联系.

本文利用前后两帧响应图的局部变化作为空间参考权重矩阵,当前后两帧响应图的局部变化较激烈时,该部分的可靠性较低,对不可靠部分执行较高的约束,反之亦然.其空间参考权重矩阵wr定义为:

(2)

公式中:Rt[ψΔ]为当前样本生成的响应图,Rt-1为上一帧样本生成的响应图.η为学习率,设置为1000;wr-1为上一帧的空间权重矩阵,w初始化为STRCF算法中固定的空间权重矩阵,即为负高斯形状的空间权重矩阵.

3.2 自适应时间正则化

STRCF算法中的时间正则项的超参数是固定的,无法自适应复杂的跟踪场景,当目标物由于快速运动、遮挡、形变、旋转等因数造成目标发生外观变化,模型因鲁棒性较差易导致跟踪漂移.故提出自适应时间正则项,根据前后两帧的异常情况获取时间正则项超参数的参考值,在跟踪的过程中利用时间正则项超参数的参考值调整时间正则项对模型的约束程度,提高模型的鲁棒性,对快速运动、遮挡、形变、旋转等场景下的目标跟踪性能有较大的提高.其参考值设置如下:

(3)

公式中:Rt[ψΔ]为当前样本生成的响应图,Rt-1为上一帧样本生成的响应图.在目标物的外观模型前后两帧变化不明显时,相应的响应图较为相似,参考值ur较大,使得时间正则项对模型的约束能力较强,能较好的避免模型发生突变.相反的,在目标物的外观模型前后两帧变化较明显时,如遮挡、目标形变或旋转、背景杂波等富有挑战性的场景,前后两帧的响应图相似程度较低,参考值ur较小,使得时间正则项对模型的约束能力较弱,目标跟踪模型需发生较大的变化以适应后续的复杂场景.为合理使用时间正则项对模型的约束能力,参数α、β分别设置为10、10.本文设置参考值ur对于时间正则项的超参数具有一定的指导意义,提高模型对复杂场景的适应能力.

3.3 目标函数及优化

本文以STRCF为基准算法,引入了基于样本可靠性的自适应时空正则项,其目标函数定义如式(4)所示:

(4)

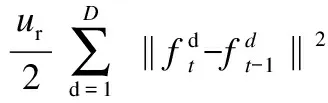
为求解公式(4),可使用交替方法乘子法(ADMM)[12]进行迭代求解,加快求解效率,提升本文目标跟踪算法的运行速度.引入辅助变量g=f,可将式(4)写出增广拉格朗日公式,即:

(5)

(6)

采用ADMM可将式(6)分解为4个子问题,其表达式为:

(7)

(8)

(9)

mi+1=mi+fi+1-gi+1

(10)

对上述4个子问题分别进行求解得最优值.

1)子问题f

子问题f计算复杂度较高,根据帕塞瓦尔定理[13]将式(7)从时域转换到频域,可显著降低算法复杂度,公式(7)转换后如下:

(11)

(12)

(13)

由于公式(13)中矩阵求逆耗时长,根据Sherman-Morrsion 公式[14]可得:

(14)

2)子问题g

对于公式(8)未存在相关性计算,因此不必引入离散傅里叶变换,可直接在时域进行求解,对公式(8)求导可得:

gi+1=(WTW+γI)-1γ(ft+mt)

(15)

式中,W=diag(w)∈RT×T为空间权重矩阵w的对角矩阵,推导可得w·h=Wh.

3)子问题w

子问题w的求解与子问题g类似,可直接在时域上对公式(9)进行求导,可得:

(16)

式中,G=diag(g)∈RT×T为辅助矩阵g的对角矩阵,推导可得g·w=Gw.

4)更新惩罚参数γ

惩罚参数γ的更新公式如下:

γi+1=min(γmax,ργ(i))

(17)

式中,γmax为γ的最大值,ρ为γ为的固定参数.

3.4 算法流程

本文算法将空间可靠性与自适应时间正则化融入到STRCF算法中实现目标跟踪,其流程如下:

1)第1帧初始化:根据视频序列初始第1帧的目标框,在目标区域提取目标的灰度、颜色属性(CN)和方向梯度直方图(HOG)特征,建立特征模型.以负高斯模型作为本文算法的空间参考权重矩阵进行初始化,自适应时间正则项超参数初始化为8,进而初始化位置滤波器和尺度滤波器.

2)目标定位及尺度估计:在下一帧输入时,在目标搜索区域内提取不同尺度的目标特征并与位置滤波器和尺度滤波器进行相关性计算,得到相应的响应图,获得目标的位置与尺度.

3)参数更新及模型训练:通过公式(2)更新空间参考权重矩阵,通过公式(3)更新时间正则项超参数,在最后根据公式(14)可对位置滤波器进行训练.

4)模型更新:采用STRCF算法中的固定更新速率对位置滤波器和尺度滤波器进行更新,以适应跟踪环境的多样性和复杂性.

5)循环跟踪:若视频序列未结束,则执行步骤2);若视频序列结束,则算法结束.

4 实验与结果分析

4.1 实验环境与参数设置

为验证本文算法的有效性,本文使用MATLAB R2019b软件以及MatConvNet工具箱在Windows操作系统下编程实现.其实验硬件平台的CPU为Intel i5-9400F,运行内存为32G.本文算法的基准算法为STRCF,尺度估计阶段,本文利用DSST[15]算法中的 33 个尺度的图像金字塔与尺度相关滤波器确定目标尺度信息,尺度个数为33,尺度因子为1.01.由于本文算法引入自适应空间正则项,其自适应空间正则项权重参数a设置为10.其余参数设置与STRCF相同.本文选用近几年优秀算法在OTB-2013[16]、OTB-2015[17]数据集进行实验和质量评估,以凸显本文算法的鲁棒性和优越性,选用的对比算法有KCF[6]、DSST[15]、SRDCF[7]、BACF[8]、STRCF[10]、ARCF[9]和AutoTracker[18].

4.2 数据集和评估标准

OTB数据集是目标跟踪领域主流的测试数据集,其包含常用跟踪场景下收集的100个视频序列,将视频序列一帧一帧分割成图片的形式,其共58897帧图片.覆盖了现实中常见的跟踪场景,如低分辨率、光照变化、平面外旋转、出视野、尺度变化、形变、遮挡、快速运动、运动模糊、平面内旋转以及背景杂乱共11种跟踪挑战,满足本文的对比试验需求.OTB2013数据集是从OTB数据集中选取了更具有挑战性的51个视频序列,大部分视频序列为灰度序列.OTB2015数据集是OTB2013数据集的扩展,具有100个视频序列,更能全面的评估算法的整体性能.在对比实验中,比较重要的两个指标是:成功率(SR)与距离精度(DP),采用一次通过评估标准(OPE).成功率(SR)表示为跟踪序列中标注目标框和跟踪目标框重叠得分大于给定阈值(td=20pixel)的帧数占比,能有效评估跟踪算法的位置与尺度的精度.距离精度(DP)为跟踪序列中目标中心定位误差小于给定阈值(t0=0.5)的帧数占比,能有效评估跟踪算法的目标定位精度.

4.3 定量分析

为检验本文目标跟踪算法的跟踪性能,选取了近几年优秀的基于相关滤波的目标跟踪算法在数据集OTB-2013与OTB-2015进行了对比实验,包含KCF、DSST、SRDCF、BACF、STRCF、ARCF和AutoTracker.图1展示了8种对比算法在OTB-2013数据集上的距离精度和成功率.图2展示了8种对比算法在OTB-2015数据集上的距离精度和成功率.由结果可知本文算法在数据集OTB-2013与OTB-2015上的表现相对于近几年的优秀算法都是较优的.本文算法在数据集OTB-2013的距离精度和成功率分别达到了87.9%和68.1%,相对于基准算法STRCF,其距离精度和成功率分别提升了1.2%和1.8%.同时本文算法在在数据集OTB-2015也取得了不错的表现,其距离精度和成功率分别达到了86.8%和66.4%,相对于基准算法STRCF,其距离精度和成功率分别提升了1.5%和1.9%.实验结果表明,本文算法根据图像的可靠性对空间正则项进行自适应更新,及时适应目标形变或遮挡情况,同时根据前后两帧的相应图的变化情况对时间正则项的超参数进行自适应的跟踪,减少模型漂移对性能的影响,提升了目标跟踪算法的性能.

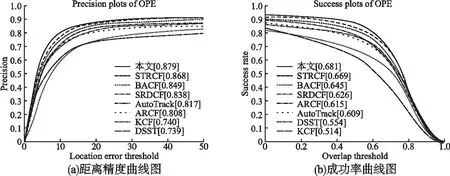
图1 OTB-2013数据集上的距离精度和成功率Fig.1 Distance accuracy and success rate on OTB-2013 dataset

图2 OTB-2015数据集上的距离精度和成功率Fig.2 Distance accuracy and success rate on OTB-2015 dataset

由于本文算法借助频域计算与ADMM算法极大的降低了本文算法目标函数的求解过程,但相对基准算法STRCF的求解,其增加了子问题W的求解以及相关参考值的计算,额外增加求解的难度,故在跟踪速度方面相对于STRCF较慢,但与同类型解决边界效应的SRDCF相比较,其跟踪速度较快.如表1所示为本文算法与DSST、SRDCF、BACF、STRCF、ARCF和AutoTracker在OTB-2015数据集上的平均跟踪速度对比情况,本文算法在数据集OTB-2015上的平均跟踪速度为23.6 frame/s,相对于STRCF仅下降了4.7 frame/s.

表1 7种算法在数据集OTB-2015上的平均跟踪速度对比Table 1 Comparison of tracking speed of seven algorithms on data set OTB-2015

本文算法相对于STRCF的成功率在数据集OTB-2015提升仅仅只有1.5%,但本文算法在STRCF的基础上加入了自适应时空正则项机制,在遮挡、形变、出视野和旋转等复杂场景下相对于STRCF具有不错的性能提升.如图3所示为本文算法与7种对比算法在数据集OTB-2015中遮挡、形变、出视野和旋转4种属性场景下的成功率曲线图.由实验结果可知:本文算法在遮挡、形变、出视野和旋转属性的视频序列上均表现良好,优于其他7种对比算法.本文算法在遮挡、形变、出视野和旋转属性的视频序列上的成功率分别为64.1%、64.2%、62.5%和64.2%,相对于STRCF分别提升了6.5%、6.3%、5.6%和3.9%.在形变和旋转属性场景下,目标会发生显著的外观变化,固定的空间权重矩阵无法自适应目标轮廓变化,使得滤波器学习到错误的样本信息以及无法充分利用正确样本信息,本文引入基于样本可靠性的自适应空间正则项,可根据目标外观变化自适应调节空间权重矩阵,提高模型在形变和旋转等属性场景下跟踪性能.在遮挡和出视野属性场景下,目标的部分有用信息丢失,容易造成跟踪漂移现象,本文算法利用前后两帧响应图的变化情况得到时间正则项超参数,对不同帧采用不同程度的时间正则项约束,避免滤波器发生突变,有效控制滤波器的更新,克服遮挡、出视野等场景对模型的干扰,提升跟踪算法的性能.

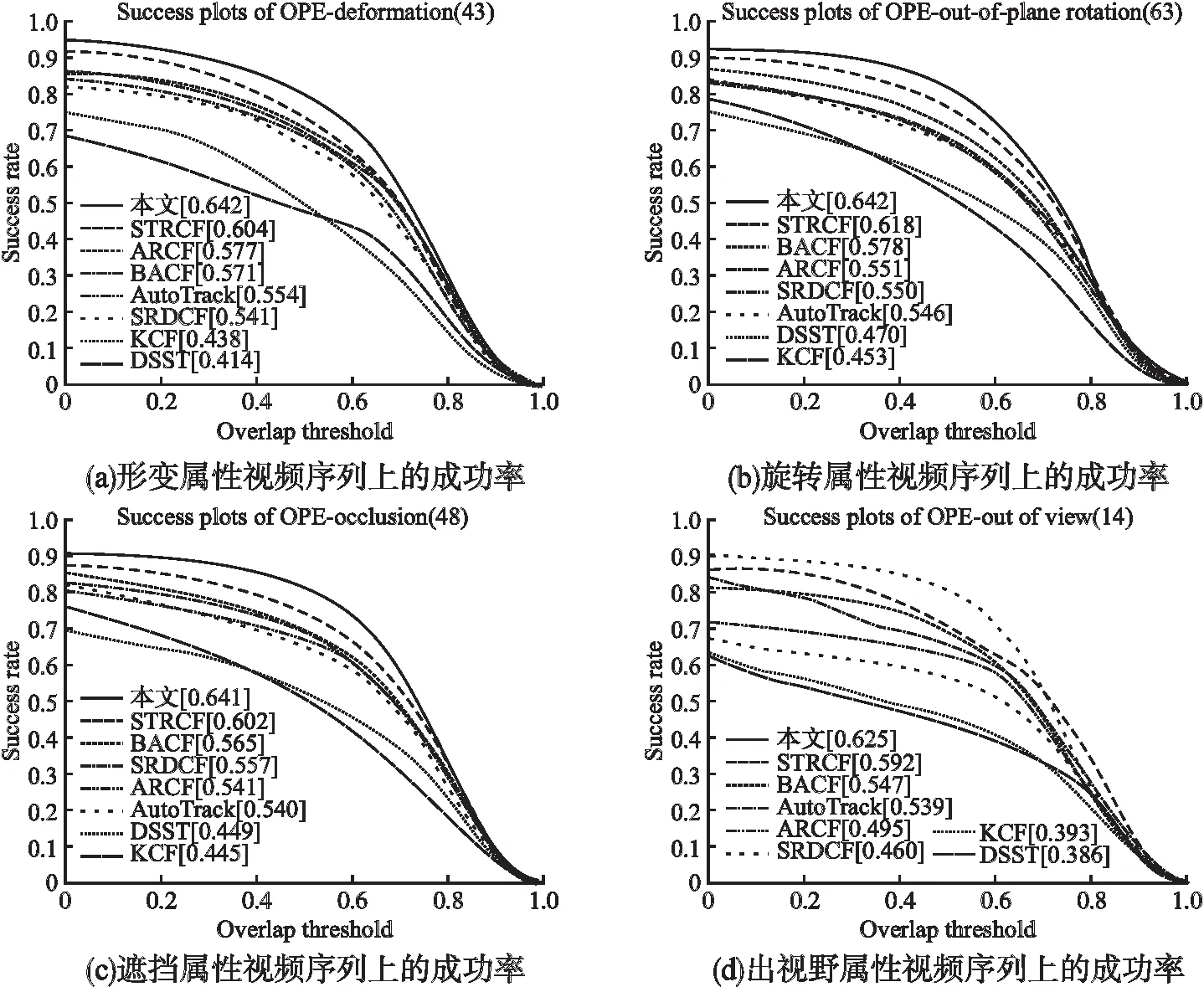
图3 OTB-2015数据集中遮挡、形变、出视野和旋转属性视频序列上的成功率Fig.3 Success rate of occlusion、 deformation、out of view and rotation attribute video sequences in OTB-2015 dataset

4.4 定性分析

为更加直观的分析评估本文算法的跟踪性能,本文利用本文算法与6种对比算法(DSST、BACF、STRCF、SRDCF、AutoTrack、ARCF)在数据集OTB-2015的4个具有挑战性属性的视频序列(Board、DragonBaby、Girl2、Shaking)进行定性分析.跟踪结果如图4所示,本文通过不同灰度和虚实线型的选框标识出各算法当前序列所跟踪到的目标位置.这4种不同属性的视频序列几乎包含了全部挑战.

图4 7种算法在4个视频序列上的跟踪结果Fig.4 Tracking results of seven algorithms on four video sequences

Board视频序列具有出视野、运动模糊、快速运动等属性.由图4(a)可知:在第103帧之前,所以算法均能较好的跟踪上目标,在第261～371帧之间发现了较大了尺度变化,DSST、AutoTrack和ARCF算法无法适应其较大的尺度变化,导致跟踪变大,将学习到过多的背景信息,后续模型的跟踪精度降低.在第585帧时,目标发生了运动模糊,导致目标外观剧烈变化,DSST、SRDCF、AutoTrack和ARCF算法无法准确的提前目标特征,从而导致跟踪漂移.到第669帧时,由于误差累计和跟踪漂移,DSST、SRDCF、AutoTrack和ARCF算法已经跟踪不上目标,只有本文算法、BACF和STRCF跟踪到目标,背景感知和空间正则项可以较好的处理出视野与运动模糊等问题.

DragonBaby视频序列具有旋转、遮挡、快速运动等属性.由图4(b)可知:由于快速运动,从第34帧开始,DSST、SRDCF和BACF算法开始出现跟踪漂移问题,其余算法由于引入了时间正则项或异常抑制机制,能较好的减少跟踪漂移.在第51帧时,只有本文算法和AutoTrack算法较好的跟踪到了目标,其余算法都未跟踪上目标,由此可见自适应时间正则项可较好的克服目标模糊、旋转、快速运行等挑战性问题.在第68～79帧时,目标发生了遮挡问题,本文算法依然可以较好的跟踪到目标,本文利用样本可靠性学习到了可靠的空间权重矩阵参考值,有效了避免了学习到错误的样本信息,避免由于目标遮挡发生漂移或跟丢现象.在第113帧时,DSST、SRDCF和BACF由于跟踪漂移误差累计不能跟踪上目标,而本文算法依然可以稳定跟上目标.

Girl2视频序列具有目标变形、遮挡、运动模糊等属性.由图4(c)可知:在第110帧时,目标发生了完全遮挡,样本可靠性较低,导致所有算法无法跟踪到正确的目标,而是跟踪到了遮挡物.在第202帧时,遮挡物离开视野范围,跟踪框停留在原地.在第344帧时,本文算法与STRCF算法重新跟踪上目标物,这是由于目标走进了目标搜索范围,滤波器在搜索范围内找到了响应最大值处.在第950～1050帧之间,镜头开始向目标物拉近,发生了较大的尺度变化,但本文算法与STRCF算法依然稳定跟踪到目标.其他算法与第110帧时跟踪情况相同,无法跟踪到目标.Shaking视频序列具有光照变化、旋转等属性.由图4(d)可知:在第15帧时,本文算法、STRCF和DSST可以稳定的跟踪到目标,其他算法都跟踪失败.在第60帧时发生了较大的光照变化,影响目标物的特征提取,此时本文算法、STRCF和DSST依然可以很好的跟踪到目标,而其他算法的偏移程度加大,未能跟踪到目标,这表明本文算法提取的HOG特征可以较好的克服光照变化.在90～160帧之间,目标物发生了较大了旋转、尺度变化,除本文算法、STRCF和DSST可以一直稳定跟踪目标外,其余算法均跟踪失败.

5 结 论

本文算法针对现有基于时空正则化相关滤波的目标跟踪算法在解决边界效应时引入的空间权重矩阵无法自适应目标变化和时间正则项超参数固定的问题,提出了基于样本可靠性的时空正则化自适应相关滤波目标跟踪算法.该算法利用响应图的局部变化和上一帧的空间权重矩阵,判断样本的空间可靠性,使滤波器充分学习到正确的目标信息.同时引入相邻两帧的响应图全局变化作为时间正则项超参数,用于约束模型的突变.采用交替方向乘子法(ADMM)进行算法的优化,迭代求解多个子问题,保证算法的运行效率.实验结果验证了本文算法的优越性,对遮挡、形变、出视野和旋转等场景提升较大,在一定程度上解决了边界效应对跟踪的影响.但本文算法在低分辨率和背景杂波场景下性能较弱,接下来的工作将以本文算法为基础,尝试把手工特征和深度特征进行自适应融合,同时利用多个相关滤波器来提升跟踪性能.