基于重加权二阶正则项的图像修复算法

郑建炜,练义欣,蒋嘉伟

(浙江工业大学 计算机科学与技术学院,杭州 310023)

1 引 言

图像作为信息传递的主要载体之一,由于其简易的表达方式而在日常生活中得到了广泛的应用.但是,在图像传输过程中,由于传感器以及存储设备的故障极易导致图像信息损坏,由于存储不当而导致图像出现划痕,由于图像分辨率降低而导致图像模糊,以上种种均会大大影响图像的后续使用.因此,图像修复(image inpainting)是一项重要的研究工作,是一种建立已知像素和未知像素之间关系的技术.在现实世界中,数据通常存在一些潜在的相关因素,如连续性、对称性、重复性等,图像修复技术基于上述特性,通过已知像素提供的信息补全未知像素,使图像信息完整,满足人类的视觉感知要求[1].图像修复作为底层视觉任务,是后续下游任务(如检测)顺利应用的基础.该项工作最早可追溯到中世纪,计算机技术与图像处理技术齐头并进,不断发展,如今,图像修复技术已经成为计算机视觉(computer vision)和计算机图形学(computer graphic)领域的重要研究方向,结合现有应用,修复的作用体现在许多科学和工程领域中,例如上下文信息识别[2]、推荐系统[3]、X射线CT中金属伪影的去除[4]以及退化图像的恢复等,也被广泛应用于影视、生活、安防等领域.

依计算技术而言,图像修复有两种主流的方法,即数据驱动法和知识驱动法.数据驱动法即以大量数据为基础的分析方法,如经典的基于深度学习的方法.在实践中,一些基于深度网络的方法,如卷积神经网络[5]和生成对抗网络[6,7],已在图像重建领域获得成功应用.然而,虽然深度学习拥有良好的性能,在分层非线性图像表示方面表现出色,但其固有缺陷仍严重阻碍了在小尺寸单张图像修复中的应用.首先,神经网络参数优化需要大量的训练时间和训练数据,进一步提升了高性能硬件需求,导致无法大规模应用于非商用家庭电脑.另一方面,尤其在图像修复领域,大多数基于深度神经网络的参数对于图像丢失区域的类型和丢失率的敏感度较高,导致扩展性能弱化.因此,本文采用基于知识驱动的单例图像修复方法,不依靠任何辅助图像或者预训练模型,只使用待测图像的先验知识引导修复问题和缩小解空间.

图像修复问题可以公式化为从一组有噪声的线性测量中恢复图像f∈m×n.

y=Φf+ε

(1)

其中ε指噪声,操作算子Φ指造成图像损坏的具体形式,如模糊、像素丢失或下采样,因此测量数据y仅捕获原始图像f的一部分.公式(1)是各类典型问题的一般化数学表达,包括去噪、去模糊、修复、超分辨率、压缩传感以及更高级的线性计算成像方式.众所周知,从部分信息中恢复原始图像是一个不适定问题.为获得可解的适定问题,需要利用图像的一些先验知识,如稀疏性、相似性、平滑性等.通常,先验知识以不同的正则项给出.在正则项约束下,图像处理问题可转化为以下优化问题:

(2)

基于扩散的方法通常以传播机制为核心,通过不同的传播策略将已知区域的信息传播到待修复区域以实现图像修复,如基于偏微分(Partial Differential Equation,PDE)的修复技术和基于几何图像模型的变分修复技术.前者将待修复区域周围的信息传播到修复区域中,典型方法包括C.Tian等[8]提出的基于偏微分方程的高效局部无纹理图像修复模型和Z.Liu等[9]提出的利用曲率扩散强度CDD(Curvature-Driven-Diffusions)的图像修复模型.后者通过建立图像的先验模型和数据模型,利用泛函和全变分知识,将图像修复问题转化为一个泛函求极值的变分问题.这类算法主要包括全变分(Total Variation,TV)模型[10]、Euler′s elastica模型[11]、Mumford-Shah模型[12]等.此类基于扩散的修复方法在处理小尺度图像破损时效果较好,但在缺失区域较大或缺失区域及周围纹理复杂时,修复效果趋于模糊.

基于样本的修复技术更加适用于大区域损坏图像的修复,可以取得较好的视觉感知效果,通过已知样本数据推测计算缺失区域信息,不但可以灵活应对缺失范围大小不一的问题,还可以修复损坏的细节纹理.此类方法一种简单经典的思路是将图像分解为结构和纹理两部分,并分别进行修复.另一种更常用、效果更佳的策略则是以设计匹配为基本原则,从全局搜索出与待修复区域相似度最高的图像块来填充缺失区域.例如Ram等人[13]提出在最短路径上对图像块进行排序,然后进行协同过滤修复.Jin和Ye等人[14]提出使用低秩Hankel结构化矩阵完成修复算法.非局部算法(如GSR[15])在每组相似图像块中应用字典学习,并以稀疏表示改善修复效果.最近,图像块低维特征被引入图像修复,有研究提出低维流形约束(Low Dimensional Manifold Model,LDMM)[16]并在修复任务中取得不错效果.但是,LDMM仅采用了拉普拉斯一阶梯度算子,难以保证重构图像的平滑性及对颜色变化的约束性.Dong等人提出一种二阶低维流形(nonlocal second order,NSR)提升了图像的平滑度[17],Zheng等人提出一种加权非局部二阶流形约束[18](weighted nonlocal second order,WNSR),在修复高光谱图像上取得了优秀的效果.在上述研究的基础上,本文将低维流形模型重新推导并理解为图像分解系数的加权正则项,并提出一种重加权的二阶低维流形正则项,进一步提升了修复效果.

2 相关工作

为更好理解所提算法,本节介绍能量集中特性、基于图像块的流形结构定义和非局部二阶低维流形算法.

2.1 能量集中特性

图像作为一种二维信号,其能量集中在少数低频分量,这是图像压缩、去噪、修复等算法的基础.图像变换是将N×N维空间图像数据变换为一组基向量空间的坐标参数,使这些离散图像信号坐标参数更集中,就意味着能够更好的利用图像中的有效信息,以达成更好的图像修复效果.通常可以根据奇异值的分布特点来判断能量是否集中,当非零元素位于矩阵对角线中,即遵循能量集中特性.非零元素集中在左上角的程度越高,即能量集中性越强.在实践中,特定域中信号表示的能量集中模式已被广泛利用,以设计更强大的正则化方案,以便从噪声测量中重建信号.局部基与非局部基本身的优势对于特定的信号处理任务具有很好的效果.已知常见的局部基如傅里叶、小波基或相关函数都具有“能量紧致”特性.非局部基一般从非线性降维或核PCA获得,被看作是定义数据集嵌入的坐标函数,通过用相对较少的基函数捕获数据中尽可能多的“奇异值”.因此数据集的大部分可变性主要在基函数中编码.流形模型具备很好的能量集中特性,在流形学习的上下文中,假设数据点是从平滑流形中采样的,对应于协方差矩阵“相对较大”特征值的特征向量的数量被视为对底层平滑流形的维数估计.为合理利用图像有效信息,保证图像修复效果,本文采用流形模型作为算法模型的基础.

2.2 块流形结构

给定图像f∈m×n,m,n分别表示图像的长度和宽度.在原始图像f上的任何坐标x∈(i,j),可定义大小为s1×s2的2D图像块pij(f).其中坐标(i,j)位于大小为s1×s2的矩形左上角,且(i,j)满足(i,j)∈{1,2,…,m}×{1,2,…,n}.令所有图像块的集合为F,定义如下:

F={pij(f):(i,j)}∈N×l,l=s1×s2

(3)

其中,N=m×n,图像块是嵌入在N×l中的低维平滑流形M(f)子样本[16],即F为f的块流形.对F做奇异值分解,可得:

F=ΦΣVT,F,Σ∈N×l,Φ∈N×N,V∈l×l

(4)

其中,ΦTΦ=IN,VTV=Il,Φ可视为F的非局部基,V为局部基.根据奇异值的分布特点,系数矩阵C=ΦTFV=Σ中的非零元素位于l×l上端的对角线中,即遵循能量集中特性.

2.3 非局部二阶低维流形

图像块所在流形维度[19]可用以下公式计算:

(5)

其中,u代表流形M上的坐标函数,梯度▽u(x,y)通常用离散设置下的非局部梯度表示:

(6)

(7)

(8)

3 重加权二阶正则项模型

本文将NSR解释为基于分解系数的正则化形式,分析得出其有效性源自将系数矩阵能量集中在上侧.在此基础上,本文算法将通过施加更强的约束项将能量集中区域向系数矩阵的左上方推动,提升了修复效果.

3.1 加权l2形式下的NSR

(9)

(10)

其中L是归一化图扩散拉普拉斯算子.因此,求解式(10)等于最小化以下目标函数:

(11)

(12)

(13)

(14)

类似于式(13)有:

(15)

(16)

3.2 重加权二阶正则模型

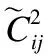
(17)

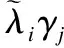
(18)

将该二次能量项代替式(11)和式(16)中的原始约束,得到以下优化问题:

(19)

使用点积分法PIM[22],式(19)的欧拉-拉格朗日方程可转化为相应的线性方程:

((γj(D-W)+λγj(D-W)T(D-W))+μW)Fvj=μWEvj,j=1,…,l

(20)

在实践中,观察到仅惩罚前几列中的系数就足以满足需求,即仅需γj,1≤j≤r,r≼l,得到:

(21)

其中Vr∈l×r由V的左r列组成,由E的其余列组成.只对式(21)右侧求和中的第1项进行加权,即替换式(18)为:

(22)

相应线性系统式(20)改为:

((γj(D-W)+λγj(D-W)T(D-W))+μW)Fvj=μWEvj,j=1,…,r(D-W+λ(D-W)T(D-W))+μW)Fvj=μWEvj,j=r+1,…,l

(23)

在本文数值实验中,令r≈0.2l,仅对前20%的列系数进行加权.采用这种加权策略,可在不影响算法性能的同时,提升计算效率.很明显,相较式(15)使用完整的SVD分解,式(16)使用局部SVD分解,可避免计算vr+1,…,vl.

(24)

总结上述过程,re-NSM模型求解过程如算法1所示.依此算法模型思路,本文进行了大量数值实验,所有结果均体现了所提re-NSM算法的优越性.

算法1.re-NSM模型

初始化：不完整的观测图像b∈N.图像块大小l,重加权前r项,r=0.2l.块矩阵F∈N×l,f(0)→F,0∈N×l→d(0).

while not converge do

1.通过SVD将F(n)进行分解获得[s1,…,sr],[v1,…,vr]

4.F(n)-d(n)→E(n)

forj=1:rdo

end for

5.解决以下线性方程获得U(n)

((D(n)-W(n))+λ(D(n)-W(n))T(D(n)-W(n)))+

8.将索引像素值重置为其已知值获得f(n+1)

9.将f(n+1)重建为F(n+1)

11.n=n+1

end while

返回f(n)

结束算法

4 算法模型实验结果与分析

为验证所提re-NSM方法在图像修复任务上的有效性,选取4种最近提出的修复算法作为对比,含NSR、加速近似梯度算法APG[23]、低维流形模算法LDMM[16],以及奇异值偏和法PSSV[24],APG利用图像的低秩性近似缺失像素.其中本文方法re-NSM、NSR、LDMM是以流形模型为基础的,算法中利用了流形结构的能量集中特性,APG、PSSV算法中不涉及能量集中体现.LDMM将图像映射在低维空间上进行模型构造和修复.NSR在LDMM基础上引入了二阶低维流形,以流形的曲率作为正则项约束修复模型.PSSV则通过优化奇异值分布重建图像.所有的对比算法均采用作者推荐的最优参数.此外,为了彻底地评价不同算法的表现,本文通过定性评价标准和定量评价标准来多方面比较各种模型的修复效果.定量评价标准包括峰值信噪比(Peak Signal to Noise Ratio,PSNR)和结构相似度(Structural Similarity Indices,SSIM).两者均是衡量图像修复质量最常用的指标,PSNR定义为:

(25)

其中MSE是均方差,可由如下公式获得:

(26)

SSIM则定义为:

(27)

4.1 实验设置

使用经典的图像处理数据集Set12,BSD68,RN16进行实验,在图1中仅展示了其中6张图片的实验效果.选取不同形式的像素丢失率和条纹设置于图像中,具体实验如下:

图1 实验所用图像Fig.1 Original image used in the experiment

实验1.5种不同的随机丢失率:60%、65%、70%、75%、80%,被独立地添加到图像中.

实验2.在50%丢失率的基础上,20条宽度为1的噪声线被随机添加到图像中.

4.2 实验结果

在实验1设置下,分别对数据集Set12、BSD68、RN16进行修复实验,论文中仅罗列出针对图像anges、hill、house、smoker、barbara、man进行修复实验的图像和数据.针对图1的6幅图像,表1详细记录了其在不同程度像素点丢失情况下的数值评价结果,其中加粗数据为最优值,次优数据用下划线表示.表2详细记录了几个数据集在不同程度像素点丢失情况下的数值评价结果的平均值,其中加粗数据为最优值,次优数据用下划线表示.图2与图3分别是实验1和实验2的可视化对比结果.

表1 实验1的定量数值评价表Table 1 Quantitative Results of Experiment 1

图3 实验2恢复结果的可视化对比,括号内为对应算法的PSNR值Fig.3 Visual comparison of the results from experiment 2,the PSNR values are also given in parentheses

从表1可以看出,在不同丢失率情况下,所提re-NSM在PSNR和SSIM上均表现最优,LDMM次之,APG和NSR的数值表现相近.不难发现,利用能量集中特性的算法都表现出较强的修复效果,可以得出能量集中在图像修复效果方面的优势.就SSIM而言,NSR和APG的数值较低,PSSV稍高一些,但与re-NSM和LDMM有一定差距,re-NSM和LDMM在数值上相差不多,但随着丢失率的降低PSNR数值差异愈加明显.对比表格中其他数据可得,6组实验中本文方法均具有最高的平均修复结果.

表2为丢失率不同的情况下,测试数据集通过各算法修复的数值结果的平均值汇总表.从表2可以看出,所提方法re-NSM较稳定,在PSNR和SSIM上均表现最优,LDMM次之.APG和NSR的数值表现相近,在PSNR和SSIM上均与本文方法存在较大差距.在像素点丢失80%的情况下,re-NSM的平均PSNR值达到32.26dB,高于次优方法LDMM 0.99dB.对比表格中其他数据,不难看出,在大量图像实验中,本文修复方法效果较稳定,均优于对比实验.

为进一步验证不同算法的视觉修复效果,图2展示了不同图像在实验1中的修复效果.由于图像数据过多,文中仅展示在像素丢失率为80%的情况下6组图像的视觉修复效果.以agnes图像实验为例,即图2中的a系列,能够明显看出APG算法修复后的图像存在一些模糊点和伪影,视觉感官较差.通过LDMM算法修复的图像有清晰的轮廓和较完整的细节,但是整体色调偏亮,与原图差异较大.通过NSR算法修复后的图像在色调上与原图较接近,但是由于二阶正则项的约束,图像修复效果偏向于平滑,损失较多图像细节.通过PSSV算法修复的图像除恢复效果一般外,额外会产生一些条纹,使得图像条纹感明显,恢复效果不佳.本文提出算法re-NSM恢复后的图像在保持平滑性的同时,保存较多精准细节,且与原图无明显色差,视觉感受上效果更佳.

从6组图像的视觉效果中可看出,APG和PSSV的修复结果会产生一些模糊点和伪影,其中PSSV会产生额外的细条纹,这可能是由于PSSV采用的低秩逼近算法将修复过程中产生的条纹视为低秩分量.而NSR算法会产生过度平滑的现象,在高丢失率的情况下,由于二阶正则项的约束,NSR的修复效果更偏向于光滑从而损失一些图像细节.LDMM算法在保存细节方面表现较好,但是图像的色彩明显偏亮,与原图存在色差.所提re-NSM同样采用了二阶正则项技术,但是所涉及的重加权策略更好地分配了能量流动,在保持平滑性的同时仍能保留更精准的细节.综合所有图像,所提方法在视觉感受上效果更佳,细节修复较好,且与原图无明显色差,证明了该方法的优越性.

实验2在6张图像上分别加入了20条噪声干扰线,图3为相应视觉修改结果以及PSNR值.可以从图3中看出,PSSV对修复条纹失效,从图像中(如图3(a)-5)可以明显看出边界清晰的条纹竖线,这说明条纹图像低秩分量有等效性,算法难以区分条纹和干净图像,即条纹被误认为干净图像的组成部分之一.APG能大致修复条纹,但仍能在数据中(如图3(a)-2,(c)-2,(e)-2)看到明显的线条痕迹和一些异常点.LDMM,NSR和re-NSM均能修复条纹和缺失像素,图像轮廓修复较好,相比之下,LDMM修复结果较模糊,放大后能看到明显的异常点,缺少细节元素.NSR的修复图像过于光滑,缺少细节元素.从数值指标PSNR和视觉效果均能看出,re-NSM表现最佳,恢复图像中看不到线条痕迹,且能较好的恢复原图内容,细节保留较多,再一次证明了所提重加权策略的有效性.

4.3 参数分析

本节对所提算法的两个重要参数进行敏感度分析,即图像补丁大小p和权重参数γ,实验在50%采样率且无条纹情况下的smoker图像进行.所有结果取自10次试验的平均值.

1)图像大小p:通过将从1调整到10,图4给出了相应的PSNR变化曲线.由图可知,本文方法在p从1调整到10的过程中,数值逐渐增大.当p>4时,数值趋于平稳.为精细化对比,图5进一步给出了p>4时的结果曲线,从中可见,PSNR获得最佳数值效果时 的大小设置为7,当p>7后PSNR呈下降趋势.因此在本文实验中,图像块大小(patch size)的默认数值设置为7.

图5 参数patch大小对PSNR的影响(P>4细节图)Fig.5 Influence of patch size on PSNR(P>4)

2)权重参数γ:参数γ是二阶正则项权重.如图6所示,随着权重参数γ的增加,所提方法的PSNR先增后减.当γ=0.01时,re-NSM取得最佳值.当γ>0.01时,数值呈下降趋势.因此γ=0.01是本文实验所用图像的推荐设置.然而,由于不同图像的特征差异,实际应用中γ的合适取值可在0.01～0.05范围内调优选择.

图6 权重参数γ大小对PSNR的影响Fig.6 Influence of weight parameter γ on PSNR

5 结 语

本文提出一种重加权的二阶低维流形正则项用于自然图像缺失像素修复.所提方法结合了图像处理的局部和非局部基,并展示了其在线性变换框架下的能量集中特性.基于此,将该特性通过图像块的局部基形式纳入之前的正则化机制,能更好地分配修复过程中的能量流动,保留更多非规则化纹理细节.所提模型使用广义最小残差分(GMRES)求解.在与多种经典和新颖算法的比较实验中证明了所提正则项的优越性.当前算法版本中,将图像块大小作为超参数且按经验设值.然而,已有分形图像压缩和深度卷积网络的工作表明同一图像中感知不同大小图像块的重要性.在之后的工作中,可以结合不同图像块尺度构建多分辨率的修复模型.此外,所提算法需要消耗较多的运行时间,后续将进一步简化二阶优化算法,提升模型应用的实时性并使之能用于自然彩图、遥感影像等更丰富的实际场景.