利用深度学习的高速网络流基数估计算法
杨东阳,韩轶凡,孙玉娥,李 姝,杜 扬,黄 河
1(苏州大学 计算机科学与技术学院,江苏 苏州 215006)
2(苏州大学 轨道交通学院,江苏 苏州 215131)
3(沈阳理工大学 装备工程学院,沈阳 110159)
1 引 言
在高速网络中实时准确地估计每条流的流量[1-21]可以为流量工程、异常检测和网络安全等提供可靠的基础数据,对大量网络应用来说至关重要.随着大网络数据时代的演化和发展,网络流速和规模日益增长.据Cisco发布的白皮书《Cisco Visual Networking Index:Forecast and Trends》[22]预测,到2022年全球的IP流量将达到每年4.8泽字节,是2017年的3.7倍.而要实时处理如此高速海量的网络数据需要消耗大量的高速存储和计算资源,这为高速处理资源极度紧缺环境下的高精度流量测量提出了严峻的挑战.
高速网络流量测量主要包括流大小测量和流基数测量,其中流大小测量主要是计算流中数据包的个数或字节数,而流基数的测量则是估计流中不同元素的数量.在这里,流和元素是可以根据应用的实际需求定义,例如将发送至同一个目的地址的所有数据包抽象为一条目的地址流,而将流中每个源地址抽象为一个元素.显然,流基数的测量由于需要去除流中的重复元素,因此比流大小测量更具挑战性.为了保证数据包能够被实时处理,目前大多数流基数测量方法利用紧凑型数据摘要(Sketch),把整个流基数记录模块全部放置在能够匹配流速的网络处理器芯片的片上存储空间.例如,文献[6]为每条流分配一个虚拟位图(virtual Bitmap),而所有的虚拟位图共享同一段实际物理内存来实现存储资源受限下的流基数估计.文献[7]则为每条流分配了一组虚拟寄存器,而让不同的流通过所有虚拟寄存器共享同一段物理内存来实现流基数估计.上述解决方案利用哈希技术将实时到达的元素随机映射到所分配实际物理空间的一个或多个比特位,并以一定概率将其置1,最终根据置位概率推导出置位结果与实际元素数量之间的关系式,从而得到流基数估计器.然后,这些机制为了尽可能地降低片上存储资源的占用,均使用比特级或寄存器级的存储资源共享技术,让多条流共享同一段物理存储空间,使得不同流的信息混杂在一起,从而为后面的流基数估计引入了噪声.为了进一步降低噪声的影响,已有机制大都通过概率分析的方式,分析出每条流引入的平均噪声,并在估计时将平均噪声滤除,进而得到一个相对准确的估计结果.
上述去除噪声的方法并不总是高效的,当实际引入的噪声与期望的平均噪声偏差较大时,会严重影响流基数的估计精度.要进一步提高流基数估计的精度,就需要设计新的方法来降低流之间存储共享所带来的噪声影响.
针对上述问题,本文在流基数估计中引入了深度学习技术,致力于降低由于存储资源共享所带来的噪声影响,进而提高流基数估计的精度.为此,本文首先借鉴已有的虚拟寄存器技术,改进了已有的数据包实时处理和记录存储方法,提出了一种更高效的寄存器数值编码技术,以尽可能地降低虚拟寄存器中的噪声并降低流基数估计的复杂度.然后,进一步引入深度学习技术,用于学习和提取置位结果与引入噪声之间的潜在模式,并依此来更好地去除噪声,提高估计精度,所提出的基于深度学习的流基数估计算法EvHLL(Enhanced virtual HyperLogLog)主要包含为每条流分配虚拟寄存器组、对元素进行哈希并根据哈希结果决定是否更新相关寄存器中的数值、对每条流所对应的寄存器组中的数值进行编码以提高流基数估计效率以及利用每条流的编码结果和训练好的深度学习模型来估计流基数4个阶段.与已有研究相比,本文的主要贡献在于:
1)改进了流元素的置位和几率存储方式,进一步增大了紧凑型数据结构的估计范围,进而减低了所需的片上存储空间.
2)设计了一种基于累进递增的寄存器更新规则,大幅降低了由概率随机性所带来的噪声,使得实际噪声更趋向于期望值.
3)提出了一种高效的数据编码方式来编码每条流的虚拟寄存器中的结果,并引入深度学习模型提取每条流编码的数据中的潜在的模式来提高基数估计的精度.
4)本文基于真实世界的数据集(CAIDA)[23]在不同的片上存储空间中进行了仿真实验.实验结果显示,相较于vHLL算法,本文提出的EvHLL算法具有更高的估计精度和更低的内存开销.
2 相关工作
为了在高速处理资源极度紧缺的环境下进行精准的流基数估计,研究者们在过去的几十年提出了大量的流基数估计算法[1-13].其中,大部分现有的算法都是利用紧凑型数据摘要(Sketch)来处理流元素并记录流基数信息,最终根据Sketch中的置位结果及置位概率推导出流基数.
例如,Bitmap算法[4]需要在网络处理器芯片的片上存储空间为每条流维护一个固定长度的位数组,对每个到达的数据包,首先提取其流标签和流元素,然后根据流标签找到记录该流信息的位数组,接着对其元素进行哈希,根据哈希结果对该位数组进行置位操作,最终根据位数组的长度及其置位结果估计每条流的基数.不同于Bitmap算法,HyperLogLog算法[5]在网络处理器芯片的片上存储空间为每条流维护了一组寄存器,对于每个数据包,同样首先提取其流标签和流元素,然后根据流标签查找其对应的寄存器组,接着将流元素哈希为一个特定长度的比特串(通常为32位),根据哈希结果的前若干位来计算该元素在该流的寄存器组中对应的寄存器,然后计算其余比特位的rank值(即其余比特位中最左边0的位置),当且仅当rank值大于寄存器中的数值时,用rank值替换掉寄存器中保存的数值,最终根据每条流寄存器组中保存的数值来估计每条流的基数.
上述方法的共同点是都需要为每条流保存单独的Sketch数据,即每条流对应单独的物理存储空间,这在仅需估计少量流的情况下具有一定的可行性.然后,在大网络数据时代,网络流量中包含了海量的流数据,极度紧缺的高速处理资源无法满足处理海量流数据所需的存储空间.为了解决Bitmap算法和HyperLogLog算法需要为每条流保存单独的Sketch数据,并单独占用一定物理存储空间造成昂贵的资源消耗的问题,Li等人[6]在Bitmap算法的基础上,通过让所有流共享网络处理器芯片中的同一段物理存储空间提出了virtual Bitmap(vBitmap)算法,其中每条流和其他流共用同一段物理存储空间(即同一个大的位图),而每条流逻辑上占用的位图称为虚拟位图;Xiao等人[7]提出了让所有流数据共享同一组寄存器的virtual HyperLogLog(vHLL)算法,其中每条流与其他流共享同一段物理存储空间,每条流逻辑上占用的寄存器组称为虚拟寄存器组.然而,让多条流共享同一段网络处理器芯片的片上存储空间会使得多条流的信息混杂在一起,从而在基数估计阶段引入大量的噪声,显著降低基数估计的精确度.
最近,利用机器学习技术(尤其是深度学习技术)来提高传统算法的性能层出不穷.例如,Hsu等人[19]利用深度学习算法基于历史数据训练了一个预言机(Oracle),通过学习数据包中五元组(源IP地址、目的IP地址、源端口、目的端口和网络协议类型)的特征来区分大小流,并用单独的片上存储空间来保存大流的信息,从而提高了每条流的频率估计的精度.Yang等人[21]利用一种通用的机器学习框架来减少Sketch的精度对网络流量特征的依赖性,并且在网络流大小、top-k流以及流的数量等任务上证明了提出的方法具有更高的性能.Cohen等人[24]利用在线机器学习算法来自适应地学习流的大小分布信息,并设计了良好的数据特征来执行网络数据流的基数估计.上述方法证明了机器学习技术可以有效的改进传统算法,并具有良好的性能.
这些工作促使思考是否可以设计一个简单有效的深度学习模型来学习每条流虚拟寄存器组存储的数据中的潜在的模式,来进一步改进具有大量噪声的vHLL基数估计算法的性能,在不增加计算复杂度的前提下提高每条流基数估计的性能,减少网络处理器片上存储空间的消耗.
3 相关方法
本章首先给出了本文所研究的问题,然后介绍了已有相关研究virtual HyperLogLog(vHLL)算法的设计思想.表1列出了本文主要使用的一些符号.

表1 主要符号及其含义Table 1 Main symbols and their meanings
3.1 问题定义
高速网络环境下的流基数估计是指在某个测量周期内估计每条流中不同元素的数量,其中流标签和元素标签可以是源IP地址、目的IP地址、源端口、目的端口或者其他特定的数据包头部字段.例如,估计发往某个特定目的IP的不同元素的数量可以有效的检测分布式拒绝服务(DDoS)攻击;测量从某个特定源IP地址发出的不同元素的数量可以检测超级传播者(Superspread)和扫描者攻击(Scanner).

3.2 vHLL基数估计算法
vHLL算法的主要思想是在HyperLogLog算法的基础上通过虚拟寄存器组的共享,从而实现利用少量的片上存储空间估计某个测量周期内所有流的基数的目标.在详细阐述vHLL算法之前,首先介绍一下物理寄存器和虚拟寄存器的区别和联系:物理寄存器是指网络处理器的片上存储空间中实际分配给基数估计算法的寄存器,而虚拟寄存器是指每条流逻辑上占用的物理寄存器,因为这些寄存器是共享的,不是单独占用的,因此称为虚拟寄存器.通过虚拟寄存器间的共享,可以大量减少片上存储空间的消耗,为其他更加重要的网络应用留下更多宝贵的片上存储资源.vHLL算法的具体过程如下所述:
假设网络处理器芯片的片上存储空间包含了m个物理寄存器,测量每条流所需的虚拟寄存器的个数为s.对于每个到达的数据包P,网络处理器会首先提取P中包含的流标签f和元素标签e,并根据流标签f来计算测量该流基数所需要的s个虚拟寄存器,将测量该流基数的s个虚拟寄存器记为:Rf={Rf1,Rf2,…,Rfs}.然后,对e执行哈希计算h′=H′(e),其中H′的哈希范围为[0,232-1),并将其表示为32位的二进制符号.接着,根据其二进制符号串中前q位的数值来计算(即将其前q位的二进制转换为十进制)该元素对应的虚拟寄存器Rfi,其中q=log2s,并计算该元素二进制符号串的后(32-q)位的rank值.最终根据式(1)来更新虚拟寄存器Rfi中存储的数值vRfi:
vRfi=max{vRfi,rank}
(1)
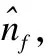
(2)
其中,αs是偏差修正常量,在实践中αs通常使用的数值是α16=0.673,α32=0.697,α64=0.709,当大于等于128时,αs=0.7213/(1+1.079/s).
公式(2)在对大流的估计上性能良好,但在小流的基数估计上往往具有严重的偏差.因此,需要对小流的估计值进行偏差修正.对于基数较小的流,将Rf视为一个具有s个比特的位数组,即将Rf中的每个虚拟寄存器Rfi转化为一个比特,当且仅当VRfi>0时,将其转换为1,否则将其转换为0,然后根据估计公式(3)估计该流的基数:
(3)
其中,V表示转换后位数组中0的个数.公式(3)仅在公式(2)的估计结果小于2.5s的时候使用以对小流基数估计结果进行偏差修正从而提高其估计精度.
4 基于深度学习的流基数估计算法
本章详细介绍了基于深度学习的流基数估计算法EvHLL.首先,从较高的角度概述了系统模型;然后,详细讨论了EvHLL算法中包含的4个主要阶段;最后,对提出的算法进行了总结.
4.1 系统模型
本文提出了一种基于深度学习的流基数估计算法EvHLL,同vHLL一样,网络处理器芯片的片上存储空间包含了由m个寄存器组成的物理寄存器组R,其中每条流仅占用s个虚拟寄存器,不同的流共享虚拟寄存器组.
网络处理器的片下存储空间包含一个基于历史数据训练好的深度学习模型M,用来根据每条流的编码结果预测其基数.在每个测量周期结束后,网络处理器芯片的片上存储空间中寄存器的数据会被离线下载到片下存储空间.每条流的虚拟寄存器中的数值会被进一步编码,从而减少输入数据的维度,并将编码结果作为输入传递给神经网络模型用于估计每条流的基数.详细的系统模型如图1所示.
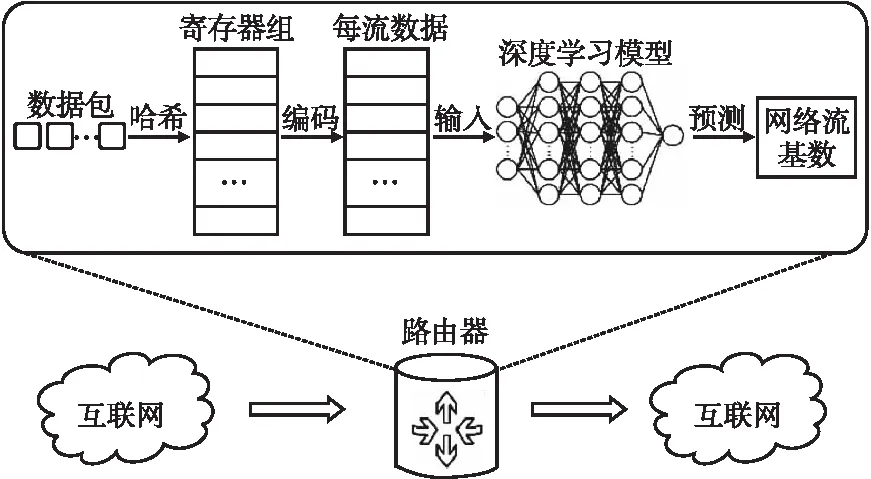
图1 系统模型Fig.1 System model
4.2 寄存器更新过程
EvHLL算法具有和vHLL算法完全不同的哈希策略和寄存器的更新规则.通过新的哈希策略,可以大幅减少网络处理器芯片的片上存储空间的损耗,通过新的寄存器更新规则,可以减少基数估计过程中由于寄存器更新过程中的噪声对估计精度带来的影响.
哈希映射策略:对于持续到达的每个数据包P,网络处理器会首先从P中提取其流标签f和元素标签e.然后,它会对e执行一个哈希运算:h″=H″(e),其中H″的取值范围是[0,2128-1).h″用128位的二进制符号串来表示.值得提前注意的是,每条流元素的最终哈希结果是一个32位的二进制比特串,将其记为B.由于每条流共享的虚拟寄存器的个数为s,用B中的前log2s位的取值决定每个元素对应的寄存器,后面32-log2s位的取值决定是否更新该寄存器中的数值.为了将h″映射到32位的比特串,将其以4比特为单位划分位32个二进制字段,每个字段与B中的每个比特位按次序一一对应.
为了使每个元素被映射到每个寄存器的概率保持一致,对于h″的前log2s个字段,当且仅当该字段对应的数值小于8(由于每个字段的取值范围为[0,16))的时候,将B中相应的比特位置1,否则该位为0.为了减少内存空间的消耗和数值噪声,对h″的后32-log2s个字段执行不一样的操作,当且仅当这些字段对应的数值小于11的时候(11在实验中具有最优的估计精度),将B中相应的比特位置1,否则该位为0.通过上述两阶段的计算,每个元素经过新的哈希策略,会被映射到32位的二进制符号串,每一位被置0或置1的概率不尽相同.具体的哈希映射策略如图2所示.
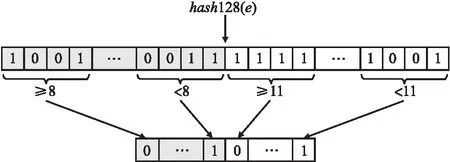
图2 哈希映射策略Fig.2 Hash map strategy
寄存器的更新:每条流的s个寄存器由预先设定的s个哈希函数{H1,H2,…,Hs}确定的,如第i个寄存器是寄存器数组R中的第Hi(f)modm个寄存器.根据每个元素e的哈希映射结果,可以计算出其对应的虚拟寄存器Rfi,即B的前log2s位对应的数值.然后计算B的后32-log2s位的rank值.当且仅当rank值满足式(4)的时候,以rank值取代寄存器中的数值:
rank=VRfi+1
(4)
通过式(4),可以消除寄存器更新过程中由于概率随机性导致的大量噪声,寄存器中的数值只会以累进加1的方式进行更新,当某个元素的哈希结果会导致出现大的偏差的时候,对应的寄存器会没有任何选择地忽略掉该异常值,并保留原先存储的数值.
通过这样的每条流元素处理方式,消除了基数估计过程中的大量随机噪声.而且实验过程中每个寄存器仅需3个比特即可满足测量要求,相比于vHLL算法,如果寄存器个数不变,内存空间将节省40%,这对于宝贵的片上空间来说是非常重要的,可以留下更多宝贵的空间给其他更加重要的应用.详细的寄存器更新过程的伪代码如算法1所示:
算法1.寄存器更新算法
输入:某测量周期内的数据包集合{P1,P2,P3,…}
输出:寄存器组中各个寄存器的值
1.for {P1,P2,P3,…}中的每个数据包P
2. 初始化B的每一个比特位的值为0
3. 提取P的流标签f和元素标签e;
4.h″=H″(e)
5. foriin {1,2,…,32}
6.ifi 7.ifh″的第i个字段的值<8 8.B[i]=1 9.else 10.ifh″的第i个字段的值<11 11.B[i]=1 12.计算其对应的寄存器Rfi,其存储的数值为VRfi 13.计算B的后32-log2s的rank值 14.ifrank=VRfi+1 15.VRfi=rank 16.returnR 对数据进行有效的编码可以在数据信息没有任何衰减的情况下有效地减少数据维度,从而提高基数估计的效率.如上所述,每个寄存器仅需3个比特即可满足测量需求,因此,每个寄存器中存储的最大数值仅能为7.在此基础上,可以利用有效的编码方式来进一步处理数据.具体的编码方式如下: 对于每条流f,令其共享的s个虚拟寄存器为{Rf1,Rf2,…,Rfs},其中Rfi=R[Hi(f)modm].然后统计该流对应的s个虚拟寄存器中包含的1,2,…,7的虚拟寄存器的个数,以一个7维数组记录每条流编码后的数据,其中第i维表示值为i的寄存器的数量.当虚拟寄存器中保留的数值为0时,不对其进行计数.最终每条流的数维度由s缩减到7,具体的编码过程如算法2所示. 算法2.数据编码 输入:流的集合{f1,f2,f3,…} 输出:每条流的编码结果 1.forfin {f1,f2,f3,…} 2.初始化7维数组rstf保存编码结果 3.foriin {1,2,…,64} 4.ifRfi不等于0 5.rstf[VRfi]=rstf[VRfi]+1 6.returnrstf 为了从每条流的编码数据中提取有效信息从而进行精确的流基数估计,本文设计了一个包含4个含参数层的全连接神经网络模型,用于进行基数估计.详细的网络模型如图3所示. 图3 神经网络模型Fig.3 Deep learning model 神经网络的输入是每条流编码的7维数组,并包含3个隐藏层,每个隐藏层的神经元的个数都是25个.所有隐藏层的神经元采用的激活函数都是ReLU(修正线性单元),它可以高效的加速神经网络的训练,避免梯度消失和梯度爆炸等问题,而且简化了网络的运算,降低了模型的复杂度.ReLU的表达式如式(5)所示: f(x)=max(0,x) (5) 模型的训练是基于历史流量数据进行的,在历史网络数据流中模拟数据处理过程,而且流的真实基数信息是可以轻易获取的,从而获得大量的训练数据.损失函数采用的是均方根误差损失,神经网络模型的优化器用的是Adam(自适应矩估计)优化方法,它经常用于解决包含很高噪声和稀疏梯度的问题. 流基数估计过程是简单且高效的,对于每条流f,仅需找到其编码后的数据rstf,然后将其作为输入传送给已经训练好的神经网络模型M,该模型会对每条流的基数进行准确的预测.具体的基数估计过程如算法3所示. 算法3.基数估计 输入:流的集合{f1,f2,f3,…} 1.forfin {f1,f2,f3,…} 2.查找rstf 本小节详细介绍了提出的基于深度学习的流基数估计算法EvHLL,该算法在vHLL的基础上重新设计了每条流元素的两阶段哈希策略及寄存器数值的更新规则,有效的减少了基于虚拟寄存器共享的vHLL基数估计算法中由于随机性而造成的大量噪声,减少了网络处理器芯片的片上存储空间的消耗,并设计了一个全连接神经网络模型来提高基数估计的性能. 本节对基于真实世界的数据集对提出的EvHLL算法进行评估.首先介绍实验采用的CAIDA数据集;其次介绍基数估计性能的评估指标;最后,展示并分析了实验结果. 在实验过程中,采用的数据集是2016年CAIDA在equinix-chicago高速监视器上被动监听的匿名流量踪迹[23].据统计,一分钟的CAIDA数据集包含了超过3千万个数据包,58万个源地址流和16万个目的地址流.用CAIDA数据集中前5分钟的数据进行相关实验,每一分钟为一个测量周期,并在目的地址流上评估了算法的性能.其中前2分钟的数据用来训练模型,第4分钟的数据作为验证集评估模型的性能,第5分钟的数据作为测试集.数据集的具体划分如表2所示. 表2 数据集Table 2 Dataset 本文采用两个常用的性能评估指标来衡量算法的精确性: 1)平均相对误差(ARE):平均相对误差的计算公式如式(6)所示: (6) 2)平均绝对误差(MAE):平均绝对误差的计算公式如式(7)所示: (7) 一般来说,相对误差往往更能反映估计的精确程度.相对于平均相对误差,平均绝对误差往往更能反映出预测值误差的实际情况. 在不同的网络处理器芯片的片上存储空间上对提出的算法和对比算法基于以上两个指标进行评估. 本文分别在128KB的片上存储空间和256KB的片上存储空间下对EvHLL算法和vHLL算法进行对比实验,并在不同的基数区间内比较两者的平均相对误差ARE.其中,基数区间在log级上进行划分.另外,在整体数据集上评估了两者的平均相对误差和平均绝对误差,实验精度如图3~图6所示. 图4和图5展示了在网络处理器芯片的片上存储空间为128KB的情况下vHLL算法和EvHLL算法的基数估计精度.通过图4可知,在片上存储空间非常有限的情况下,vHLL对小流的误差几乎没有任何修正效果,从而导致对小流的基数估计仍然具有较大的偏差,这说明vHLL的修正算法具有一定的局限性.然而,小流的基数在一些情况下是特别重要的,如隐匿的DDoS攻击[25].图5显示EvHLL算法在小流基数估计方面具有更高的估计精度. 图4 vHLL在128KB的片上存储空间下的每条网络流的基数估计结果Fig.4 Per-flow cardinality estimation results of vHLL under 128KB on-chip memory space 图5 EvHLL在128KB的片上存储空间下的每条网络流的基数估计结果Fig.5 Per-flow cardinality estimation results of EvHLL under 128KB on-chip memory space 图6和图7显示了在网络处理器芯片的片上存储空间为256KB的情况下两者的估计精度,可以看出EvHLL算法相较于vHLL无论对于小流的基数还是大流的基数都有更高的估计精度. 图6 vHLL在256KB的片上存储空间下的每条网络流的基数估计结果Fig.6 Per-flow cardinality estimation results of vHLL under 256KB on-chip memory space 图7 EvHLL在256KB的片上存储空间下的每条网络流的基数估计结果Fig.7 Per-flow cardinality estimation results of EvHLL under 256KB on-chip memory space 表3和表4分别列举了不同的基数区间内,两者的平均相对误差.从表3中知在128KB片上存储空间时,在基数区间为1到10时,EvHLL的ARE减少了99.15%;在基数区间为10到100时,EvHLL的ARE减少了92.41%;在基数区间为100到1000时,EvHLL的ARE减少了89.67%;在基数区间为1000到10000时,EvHLL的ARE减少了13.34%.同样,在表4中可以看到在内存空间为256KB的情况下,EvHLL算法同样具有更低的平均相对误差. 表3 128KB片上存储空间下不同基数区间的ARETable 3 ARE in distinct cardinality intervals under 28KB on-chip memory space 表4 256KB片上存储空间下不同基数区间的ARETable 4 ARE in distinct cardinality intervals under 128KB on-chip memory space 表5展示了整个测试集上在不同的片上存储空间下的估计精度.可以看到,在128KB的内存空间下,EvHLL的ARE减少了99.13%,MSE减少了98.37%;在256KB的内存空间下,EvHLL的ARE减少了82.39%,MSE减少了68.05%.整体看来,EvHLL算法远远优于vHLL. 表5 128KB和256KB片上存储空间下的整体估计指标Table 5 Overall estimation metrics under 128KB and 256KB on-chip memory space 本文提出的EvHLL算法在数据包处理及Sketch更新过程中仅需使用速度极高的片上存储(SRAM)并且仅需一次内存访问,可以实现以线性速度高效的处理每一个数据包.然而,由于查询过程中需要一定的内存访问和计算资源,且受限于SRAM的制造工艺和高昂价格,如同vHLL,EvHLL算法的查询过程在容量不受限的片下存储空间(DRAM)进行.在每一个测量周期结束后,所有数据被下载到片下存储空间,并对其进一步处理.训练好的深度学习模型置于片下存储空间,以响应每条流的基数查询.实验结果表明,本文提出的学习模型响应每条流的基数查询仅需29.35us,完全满足相关的测量需求. 此外,为了验证机器学习算法的适应性,我们在其他现实世界的数据集[26]上进行了相关实验,实验结果如表6所示,可以看到,在128KB的内存空间下,EvHLL的ARE减少了99.56%,MSE减少了99.18%;在256KB的内存空间下,EvHLL的ARE减少了95.34%,MSE减少了87.65%. 表6 128KB和256KB片上存储空间下的整体估计指标Table 6 Overall estimation metrics under 128KB and 256KB on-chip memory space 本文提出了一种基于深度学习的流基数估计算法EvHLL.在vHLL的基础上,重新设计了每条流元素的哈希策略,减少了内存空间的消耗,重新制定了寄存器的更新规则,减少了概率算法中由于随机性的存在而导致的大量噪声.采用了一种高效的数据编码方式,用于减少输入数据的维度.本文设计了一个深度学习模型,用于从每条流的编码数据中提取潜在的信息提高基数估计的性能.基于真实世界的CAIDA数据集的实验结果表明,EvHLL算法在相同的存储空间的条件下,具有更低的平均相对误差和更低的平均绝对误差.4.3 数据编码
4.4 深度学习模型及其训练
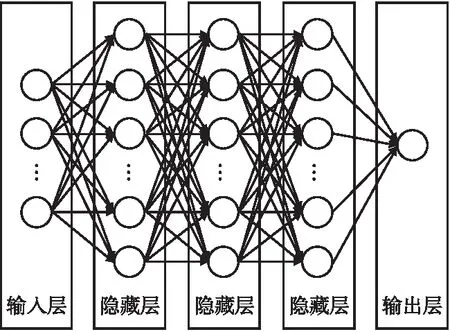
4.5 基数估计过程
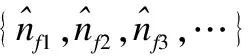
4.6 小 结
5 实验分析
5.1 数据集

5.2 性能评估指标
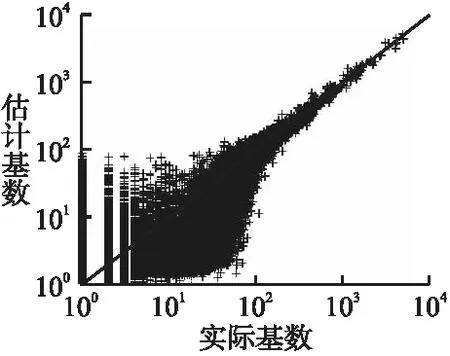
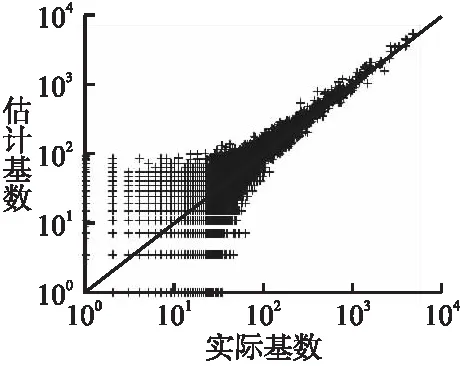
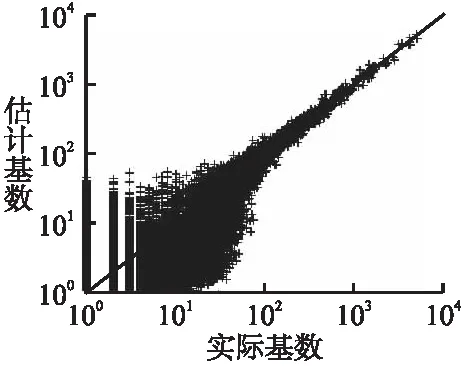
5.3 实验结果




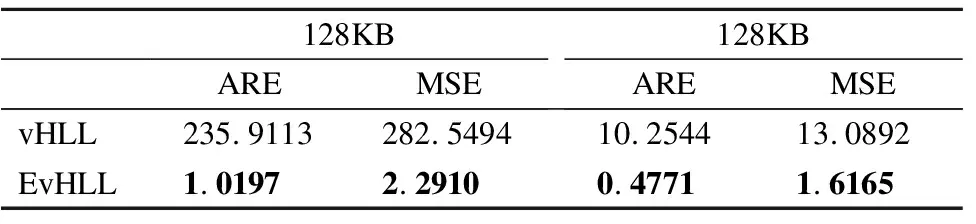
5.4 性能分析
6 结 论

