一种结合自适应近邻与密度峰值的加权模糊聚类算法

张春昊,解 滨,2,3,张喜梅,徐童童

1(河北师范大学 计算机与网络空间安全学院,石家庄 050024)

2(河北师范大学 供应链大数据分析与数据安全河北省工程研究中心,石家庄 050024)

3(河北师范大学 河北省网络与信息安全重点实验室,石家庄 050024)

1 引 言

聚类,顾名思义即“物以类聚”,其目的是将相似程度高的样本划分到同一个簇中,将相似程度低的样本划分到不同的簇中[1].聚类作为无监督机器学习领域的重要方法,在数据挖掘、模式识别、信息检索和图像识别等领域有着广泛的应用[2,3].由于其适用于无标签数据集,且能取得较好的效果,因此一直受到众多学者的关注和研究.传统的聚类方法基本可以分为基于密度的聚类方法、基于网格的聚类方法、基于层次的聚类方法、基于模型的聚类方法和基于划分的聚类方法[4].其中,以DBSCAN[5](density based spatial clustering of application with noise)和DPC[6](clustering by fast search and find of density peaks)为代表的基于密度的聚类算法泛化能力较强.DBSCAN算法在邻域半径参数和核心对象邻域包含的最少样本数设置适当时,能快速发现任意形状的类簇,但是如何设置这两个参数缺乏理论依据[7].DPC算法能快速发现任意形状数据集的密度峰值点作为聚类中心,然后将剩余样本分配给密度比它大的最近邻样本所在的簇,该算法无需迭代,适用于大规模数据的聚类分析.然而,DPC算法在样本密度度量方面没有统一的度量准则,一旦聚类中心选择错误,在剩余样本分配时容易发生连带错误[8].基于网格的聚类方法[9]用不同的网格对空间进行划分,但如何设置网格的粒度缺乏理论依据.层次聚类算法[10]可解释性较强,但是计算复杂度较高且容易聚类成链状.K-means算法[11]和FCM算法[12]是基于划分思想的聚类算法,因其算法简洁,运行速度快而吸引着众多学者的关注和研究.在传统的K-means聚类算法中,认为任意一个样本和簇的关系是属于或者不属于的关系,是对样本的硬划分,聚类效果具有局限性,而FCM算法认为任意一个样本和每一个簇之间的关系是多大程度上属于,任意一个样本隶属于所有簇的程度之和为1.该算法通过迭代来最小化目标函数,直到目标函数改变量小于阈值或迭代次数达到设定值,则停止迭代,最后,将隶属度矩阵去模糊化得到样本属于每一个簇的确切划分.因此,FCM算法是基于软划分[13]思想,相对于硬划分更为合理.然而,在传统的FCM算法中,由于初始聚类中心选取的随机性影响了聚类结果的稳定,本文将首先针对该问题对FCM聚类算法进行改进.

XI等人为了改进FCM算法对初始聚类中心敏感和易陷入局部最优的缺陷[14],将FCM算法和具有较强全局优化能力的人工鱼群算法相结合,引入自适应机制,提出了一种基于人工鱼群优化的模糊C均值聚类算法(AAFSA-FCM)[15],从而提高了收敛速度和聚类效果.然而该算法引入了大量的超参数,且未给出针对不同数据集如何调参才能达到较好的效果的方法,因此算法的泛化能力较弱.唐成华等人[16]将层次聚类和遗传算法相结合提出了一种AGFCM算法,首先通过层次聚类算法改善了FCM算法对初始聚类中心敏感的问题,再利用遗传算法的全局搜索能力克服了其在迭代时容易陷入局部最优的缺点.但是由于层次聚类本身的局限性,聚类中心的选取往往偏差较大且遗传算法同样引入了大量的超参数.张煜等人[17]提出了一种基于密度峰值的加权犹豫模糊聚类算法(WHFDP),利用密度峰值聚类算法(DPC)中的密度峰值思想来寻找初始聚类中心,用以解决FCM算法对初始聚类中心敏感的问题,但是,该算法在寻找密度峰值过程中需要主观选择截断距离,且针对不同规模数据集需采用不同的样本密度度量准则,这导致针对不同规模的数据集如何选择合适的密度度量方式没有明确定论.谢娟英等人[8]针对DPC算法中样本局部密度定义的缺陷,提出一种基于K近邻优化的密度峰值快速搜索聚类算法,算法利用样本的K近邻信息定义样本的局部密度,搜索和发现样本的密度峰值,以密度峰值点样本作为初始聚类中心.但是K近邻算法的K值仍需要人为设定,针对不同规模、不同结构的数据集如何选择合适的K值未给出有效的说明.因此,本文在现有研究基础上进一步引入了自适应近邻,根据每个样本局部的稠密程度自适应的选择该样本的近邻集合,结合密度峰值思想提出了一种自适应近邻密度峰值算法(adaptive nearest neighbors and density peaks, ANNDP),统一了不同数据集样本局部密度的度量方式,在计算局部密度时由于仅需考虑近邻样本减少了计算量,且避免了K值的人为给定,提高了模型的泛化能力.

在传统的FCM算法中忽视了每个样本对于最终聚类结果的影响程度不同.LI等人[18]提出了FWCM算法,引入了加权平均的概念重新定义了FCM算法中聚类中心的计算方式,将每个样本的重要程度按照它对聚类结果的影响分别对待.HUNG等人[19]在FWCM算法的基础上提出了NW-FCM算法,与FWCM算法相比,NW-FCM算法包含每个簇的质心以提高稳定性,该算法比FCM算法和FWCM算法具有更高的分类精度和稳定性.但这两种方法都忽略了样本不同特征的重要程度对聚类结果的影响.因此,本文在NW-FCM的基础上引入了信息熵对样本的不同特征赋予不同的权重,改进算法的迭代公式,重新定义模糊聚类中心,利用拉格朗日乘子法交替优化得到隶属度矩阵,最后将隶属度矩阵去模糊化得到最终的聚类结果.

综合初始聚类中心的选取和考虑样本特征及样本自身重要度,本文提出了一种结合自适应近邻和密度峰值思想的基于信息熵加权的模糊聚类算法(weighted fuzzy clustering algorithm combining adaptive nearest neighbors and density peaks, ANNDP-WFCM).算法的改进工作有如下3个方面:1)针对FCM算法对初始聚类中心敏感的问题,提出了一种结合自适应近邻的密度峰值算法(ANNDP)来自动搜索初始聚类中心,利用自适应邻域集合统一了DPC算法中样本局部密度的度量方式,不仅减少了计算量且针对不同规模、不同结构的数据集,可以自适应的找到每个样本的近邻集合,根据近邻信息定义样本的局部密度,搜索和发现数据集的密度峰值,以密度峰值点样本作为初始聚类中心;2)针对不同样本、同一样本不同的特征对聚类结果影响不同的问题.在NW-FCM算法的基础上引入信息熵进行特征赋权,提出了加权模糊聚类算法(WFCM).通过将ANNDP算法得到的初始聚类中心与WFCM算法相结合,重新定义目标函数中的模糊聚类中心,改进算法的目标函数,利用拉格朗日乘子法交替寻优,对最终的隶属度矩阵去模糊化得到聚类结果;3)针对输入初始聚类中心后,模糊聚类中心的求解方法不适用于包含重复样本的数据集的问题和初始隶属度矩阵无法赋值的情况,通过对初始聚类中心样本硬划分其余样本软划分来优化初始隶属度矩阵,解决了上述问题的同时减少了迭代次数.

2 相关工作

2.1 FCM算法

给定数据集X=(x1,x2,…,xN)∈RD×N,将第j个样本xj属于第i类的程度定义为隶属值μij,FCM算法[12]通过迭代使目标函数最小化,然后,将迭代后的隶属度矩阵去模糊化得到每个样本属于某个类簇的确切划分.FCM算法的目标函数为:

(1)

其中,μij∈[0,1]是样本xj隶属于第i类的程度.ci是第i簇的模糊聚类中心,N是样本个数,C是样本的类簇数,m∈(1,∞)是一个模糊值.

FCM算法过程如下:

第1步.初始化隶属度矩阵

(2)

其中,随机隶属值μij满足第j个样本隶属于所有类别的程度之和为1.

第2步.计算模糊聚类中心

(3)

第3步.更新隶属值

(4)

进而更新隶属度矩阵U.

第4步.重复执行第2步和第3步,直到隶属值在最新的两次迭代中的改变量小于给定阈值或迭代次数达到设定值时停止迭代.将最新的隶属度矩阵去模糊化,得到聚类结果.

2.2 FWCM算法

FWCM是一种根据样本之间距离的大小进行样本加权的算法[18].假设样本xj属于第i类,计算xj与其他样本的距离,利用样本之间距离的倒数作为权重对样本进行加权,引入加权平均的概念,重新定义了模糊聚类中心,使目标函数更容易收敛到最小值.若存在某样本距离样本xj很近但是和样本xj不属于同一类,隶属值μij会将其重要性弱化,改进的模糊聚类中心被重新定义为:

(5)

FWCM的目标函数为:

(6)

FWCM算法过程如下:

第1步.利用公式(2)初始化隶属度矩阵.

第2步.结合当前的隶属值,利用公式(5)计算模糊聚类中心Mij.

第3步.结合当前的模糊聚类中心Mij和隶属值μij,更新拉格朗日乘子λj为:

(7)

第4步.结合当前的模糊聚类中心Mij和拉格朗日乘子λj,更新隶属值μij为:

(8)

进而更新隶属度矩阵U.

第5步.重复执行第2步～第4步,直到隶属值在最新的两次迭代中的改变量小于给定阈值或迭代次数达到设定值时停止迭代.将最新的隶属度矩阵去模糊化,得到聚类结果.

FWCM算法由于考虑到了每个样本对于聚类中心的贡献程度不同,用样本之间距离的倒数对每个样本进行加权,距离近的样本权重大,距离远的样本权重小,进而提高了聚类效果.该算法存在两方面问题:1)由于利用样本之间距离的倒数作为权重,对于包含重复样本的数据集会出现分母为零导致改进的模糊聚类中心公式无法使用的情况;2)对于样本的特征的重要度未加区分.而在真实的数据集中,样本特征在区分样本时的作用是不同的,因此不同特征对于数据的聚类结果影响程度也不同.

2.3 NW-FCM算法

NW-FCM算法[19]与FCM算法相比,主要特点是包含加权平均值以提高精度,与FWCM算法相比,包含每个簇的质心以提高稳定性.该方法是改进FCM算法和FWCM算法.换言之,NW-FCM算法比FWCM算法更稳定,获得了比FCM算法更高的数据分类精度.在FWCM算法中,加权平均值是基于所考虑的点和其余样本计算的,而在NW-FCM算法中,加权平均值是基于聚类中心和其余样本计算的.这使得NW-FCM算法在将样本分配到特定簇时比FWCM算法更精确.由于加权平均值是结合聚类中心计算得到的,因此该算法比FWCM算法计算量更小.

NW-FCM算法过程如下:

第1步.利用公式(2)初始化隶属度矩阵.

第2步.结合当前的隶属值,利用公式(3)计算模糊聚类中心.

第3步.结合当前的隶属值μij和模糊聚类中心ci,计算改进的模糊聚类中心:

(9)

第4步.结合当前的模糊聚类中心Mij和隶属值μij,利用公式(7)更新拉格朗日乘子λj.

第5步.结合当前的模糊聚类中心Mij和拉格朗日乘子λj,利用公式(8)更新隶属值μij,进而更新隶属度矩阵U.

第6步.重复执行第2步～第5步,直到隶属值在最新的两次迭代中的改变量小于给定阈值或迭代次数达到设定值时停止迭代.将最新的隶属度矩阵去模糊化,得到聚类结果.

NW-FCM算法只是将FWCM算法中模糊聚类中心的定义进行了改进,增强了聚类结果的稳定性.但是NW-FCM算法仍然具有FWCM算法的其他缺陷.

2.4 DPC算法

基于快速搜索和发现密度峰值的聚类算法(DPC)是Rodriguez等人[6]提出的一种聚类算法,该算法能够自动地发现任意形状数据集的聚类中心,然后通过将剩余样本分配到密度比它大的最近邻样本所在的簇实现对数据集的聚类.由于操作简单,无需迭代,受到众多学者的关注和研究.该算法基于两个基本假设:1)聚类中心(密度峰值点)的局部密度大于围绕它的邻居的局部密度;2)不同聚类中心之间的距离相对较远.为了找到同时满足这两个条件的聚类中心,该算法引入了局部密度的定义.

假设样本xi的局部密度为ρi,样本xi到局部密度比它大且距离它最近的样本xj的距离为δi,对于大规模数据集,DPC算法采用截断函数定义样本的局部密度,其局部密度定义为:

(10)

其中,

距离δi定义为:

(11)

其中,dij为样本xi和样本xj之间的距离,dc为人为设定的截断距离.

对于小规模数据集,DPC算法采用高斯核函数定义样本的局部密度,其局部密度公式定义为:

(12)

DPC算法对任意两个数据点计算它们之间的距离,并依据截断距离dc计算出任意样本xi的ρi和δi.将ρi×δi相对较高的样本标记为聚类中心,将ρi相对较低但是δi相对较高的样本标记为噪声点.然后,将剩余的样本分配到距离它最近且密度比它大的样本所在的簇.该算法对于截断距离dc的选取受人为影响较大,截断距离dc的选取不合适将会导致ρi和δi计算出现较大偏差,选出错误的聚类中心,进而导致在剩余样本的分配时会发生连带错误.同时,该算法对于不同大小的数据集采用不同的密度度量方式,但是现实中对于数据集大小的界定并没有精准论断.

3 自适应加权模糊聚类算法(ANNDP-WFCM)

3.1 结合自适应近邻和密度峰值的初始聚类中心选取(ANNDP)

在基于快速搜索和发现密度峰值的聚类算法(DPC)中,聚类过程可以分为两部分:第1部分是选取密度峰值点,第2部分是剩余样本的分配.谢娟英等人针对DPC算法中样本局部密度定义的缺陷,提出一种基于K近邻优化的密度峰值快速搜索聚类算法,算法利用样本的K近邻信息定义样本的局部密度,搜索和发现样本的密度峰值,以密度峰值点样本作为聚类中心[8].但该方法中的K值仍需要人为设定,针对不同规模、不同结构的数据集如何选择合适的K值未给出有效的定论.本文提出一种结合自适应近邻与密度峰值的初始聚类中心搜索算法(ANNDP),无需设定K值,根据样本局部的稠密情况自适应选择近邻数量,结合密度峰值快速选出初始聚类中心,有效避免了模糊聚类算法中随机选择初始聚类中心导致的聚类结果不稳定性.

图1随机生成的数据集将K近邻和自适应近邻进行对比,以样本1和样本2为例,周围浅色样本分别为其近邻.在图1(a)中,由于K值的固定导致样本1必须找到距离它最近的3个样本,即使所处位置较为稀疏.而样本2即使所处位置较为稠密由于K值的限制只能将最近的3个样本作为它的近邻集合.图1(b)可以根据样本局部的稠密情况自适应的找到邻域集合.

图1Fig.1

定义1.有序距离序列.给定数据集X=(x1,x2,…,xN)∈RD×N,任意样本xi的有序距离序列为:

seq(xi)=(x(i,1),x(i,2),…,x(i,N-1))

其中,对于任意样本xi∈RD,计算除样本xi外所有样本与样本xi之间的距离,并按距离从小到大将样本排序并重新编号,形成有序距离序列.其中x(i,1)为距离样本xi最近的第1个样本,x(i,2)为距离样本xi最近的第2个样本,x(i,N-1)为距离样本xi最近的第N-1个样本,即距离样本xi最远的样本.

图2以5个样本为例展示了以样本xi为中心,其他样本的命名情况,根据距离样本xi的距离大小,其余4个样本依次被命名为x(i,1),x(i,2),x(i,3),x(i,4),则样本xi的有序距离序列为x(i,1),x(i,2),x(i,3),x(i,4).

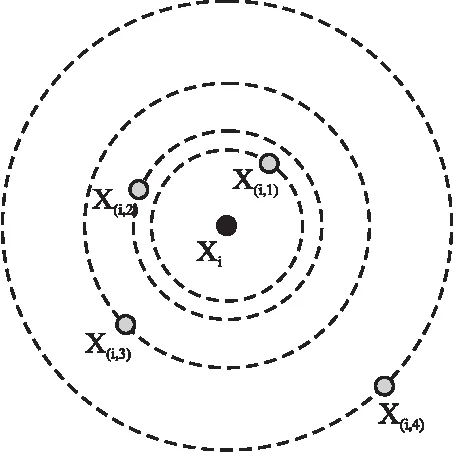
图2 有序距离序列示例Fig.2 Example of ordered distance series

定义2.自适应平均距离.给定数据集X=(x1,x2,…,xN)∈RD×N,样本xi的有序距离序列为seq(xi)=(x(i,1),x(i,2),…,x(i,N-1)).称:

(13)

为样本xi的自适应平均距离.其中,Δi(xi,x(i,N-1))为样本xi和距离样本xi最远的样本x(i,N-1)之间的距离,Δi(xi,x(i,1))为样本xi和距离样本xi最近的样本x(i,1)之间的距离.N-2为距离样本xi最远的样本x(i,N-1)和距离样本xi最近的样本x(i,1)之间的间隔数.如图2所示,距离xi最远的样本x(i,4)和距离xi最近的样本x(i,1)之间的间隔为3.

定义3.自适应截断距离.给定数据集X=(x1,x2,…,xN)∈RD×N,每个样本xi的自适应平均距离为Adapt_Dis(xi).称:

(14)

为自适应截断距离.其中κ为间隔因子,用于控制自适应邻域半径的大小.算法中以κ倍的自适应平均距离的均值作为能够接受的最大的自适应截断距离.在该截断距离内的样本集合称为样本xi的自适应近邻样本集合ANN(xi),每个样本xi根据自身的稠密情况自适应的选择其近邻个数以及近邻样本.间隔因子κ一般取大于1的常数,通过大量实验发现κ取值范围为[1.5,3]时可以更好的反映数据集局部样本的稠密情况,超出该范围容易导致自适应邻域半径超过类簇半径,使得类簇中心的定位出现偏差,影响后续模糊聚类的收敛速度和聚类精度.在本文算法中,间隔因子取1.5,具体应用中可有一定的调整.

定义4.自适应局部密度.给定数据集X=(x1,x2,…,xN)∈RD×N,称:

(15)

为样本xi的自适应局部密度.其中,ANN(xi)为样本xi的自适应近邻样本的集合,dij为样本xi和样本xj之间的距离,|ANN(xi)|为样本xi自适应近邻样本集合中样本的个数.

最后利用公式(15)计算ρi,利用公式(11)计算δi,将ρi×δi相对较高的样本标记为类簇的中心.具体流程如算法1所示.

3.2 基于信息熵加权的模糊聚类算法(WFCM)

利用信息熵[20]对数据集中每一个特征进行加权的基本思想是根据样本特征信息熵的变化程度来确定权重.若数据集的某个特征的信息熵Ej很小,说明该特征可以提供更多的信息量,在聚类分析中所能起到的作用也越大,因此该特征的权重也就越大.反之,某个特征的信息熵Ej很大,提供的信息量也越少,其权重也就越小.

首先,为了减少量纲的影响,由:

(16)

对数据进行最大最小归一化处理.其中xij表示第i个样本的第j个特征,xj表示样本的第j个特征构成的向量.

由:

(17)

计算第i个样本的第j个特征所占的比重.

由:

(18)

计算第j个特征的信息熵,若Pij=0,定义0log(0)=0.

由:

(19)

计算第j个特征的权重.

则WFCM算法的模糊聚类中心改进为:

(20)

其中,wl,l=1,2,…,L为样本第l个特征的权重.

WFCM算法的目标函数改进为:

(21)

结合约束条件引入拉格朗日乘子λj构造拉格朗日函数为:

(22)

结合当前的模糊聚类中心Mij和权重w,更新拉格朗日乘子λj为:

(23)

结合模糊聚类中心Mij和拉格朗日乘子λj,以及权重w,更新隶属度为:

(24)

其中,具体流程如算法2所示.

3.3 ANNDP-WFCM算法

由于ANNDP算法计算出来的初始聚类中心是数据集中的某一个具体样本,因此在计算改进的模糊聚类中心Mij会出现分母为零的情况,即使在FWCM算法中,若原数据集中包含重复的样本,仍会出现分母为零导致无法计算的情况,因此对Mij进一步改进,使其适用于所有数据集.

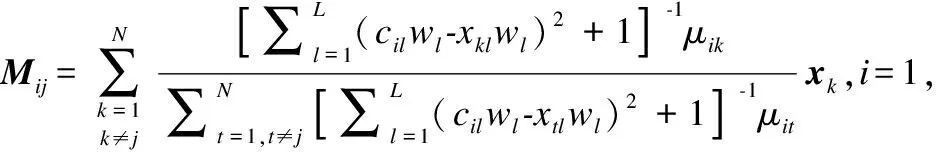
(25)

由于本算法分两步进行,在自适应近邻密度峰值算法(ANNDP)找到初始聚类中心后,将初始聚类中心输入到加权模糊聚类算法(WFCM)中.因此,首次计算Mij时需提前知道初始聚类中心ci的值以及初始隶属度矩阵U,若初始隶属度矩阵仍随机初始化,便失去了提前寻找初始聚类中心以提高迭代速度的意义.因此,本文在首次计算Mij之前仍需利用初始聚类中心ci计算出当前的初始隶属度矩阵U,该过程若用传统FCM算法中求取隶属度矩阵U的方法也会出现分母为零的情况,本文将数据集中与初始聚类中心重合的样本进行硬划分,将不与初始聚类中心重合的样本进行软划分.初始隶属值更新为:

(26)

算法1.结合自适应近邻的密度峰值算法(ANNDP)

1.fori=1,2,…,Ndo

2. 计算样本xi的有序距离序列seq(xi)

3. 根据公式(13)计算样本xi的自适应平均距离Adapt_Dis(xi)

4.end for

5.fori=1,2,…,Ndo

6. 根据公式(14)计算样本xi的自适应截断距离ΔAdapt

7. 找出以样本xi为中心包含在自适应截断距离内的自适应近邻集合ANN(xi)

8. 利用公式(15)计算样本xi的局部密度ρi

9.end for

10.fori=1,2,…,Ndo

11. 利用公式(11)计算样本xi的δi值

12.end for

13.选择ρi×δi较大的样本作为初始聚类中心

算法2.基于信息熵加权的模糊聚类算法(ANNDP-WFCM)

输出：最终聚类结果

1.根据算法1得到初始聚类中心C

2.根据公式(26)计算初始隶属度矩阵U

3.根据公式(25)计算改进的模糊聚类中心Mij

4.根据公式(21)计算目标函数JANNDP-WFCM的值

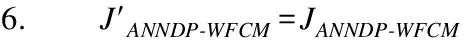
7. 根据公式(23)计算拉格朗日乘子λj

8. 根据公式(24)更新隶属度矩阵U

9. 根据公式(3)更新模糊聚类中心C

10. 根据公式(20)更新改进的模糊聚类中心Mij

11. 根据公式(21)更新目标函数JANNDP-WFCM的值

12.end while

13.将最后的隶属度矩阵去模糊化,得到样本属于某一类簇的确切划分

4 实验结果与分析

本文首先将找到的初始聚类中心在二维数据集Aggregation、Flame、4k2_far、D31、G2_2_30、Jain、R15中可视化,验证了ANNDP算法寻找初始聚类中心的有效性.然后采用真实数据集Iris、Wine、Seeds、SPECT、Haberman、Bupa、Leuk72_3k与FCM算法、FWCM算法、NW-FCM算法、FDP-FCM算法[21]、KDPC-FCM算法[22]进行对比实验,验证了本文提出的ANNDP-WFCM算法的有效性.本文所提到的算法均采用Python 3.7实现,模糊值m=2.所有实验的环境均为Windows 10 64bit操作系统,PyCharm Community 2020.3.2,12GB内存,Intel(R)Core(TM)i5-4210H CPU @ 2.90GHz.

4.1 数据集

Iris数据集、Wine数据集、Seeds数据集、Haberman数据集和Bupa数据集均来自UCI数据集(https://archive.ics.uci.edu/),SPECT和Leuk72_3k也为真实数据集[23].本文实验所用人工数据集和真实数据集如表1和表2所示.

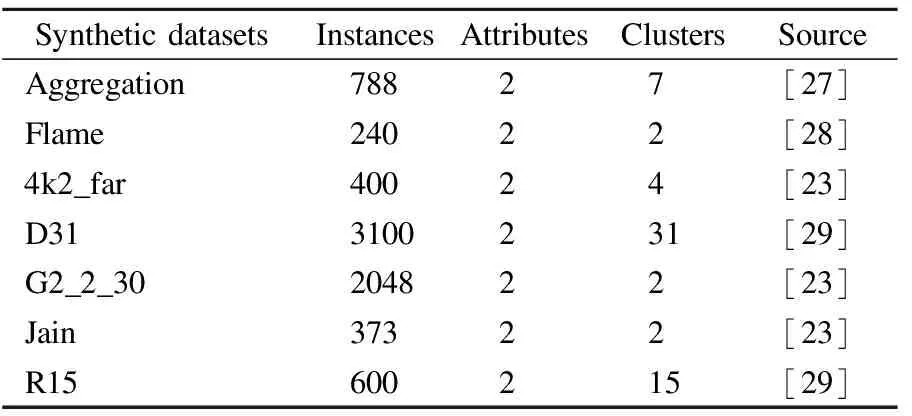
表1 人工数据集Table 1 Synthetic datasets

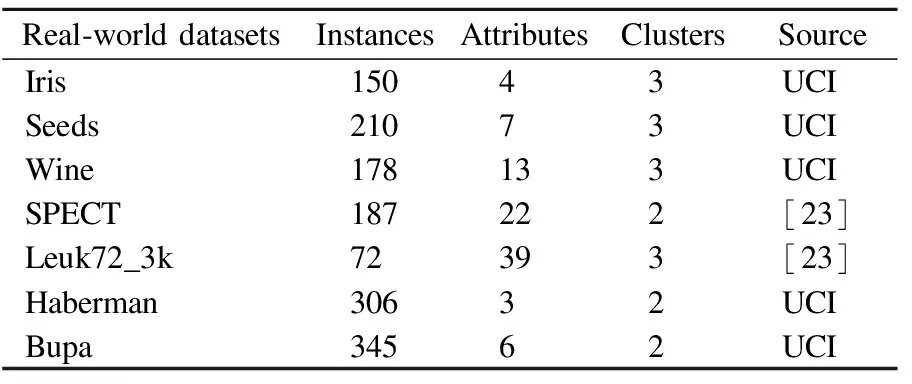
表2 真实数据集Table 2 Real-world datasets

4.2 评价指标

实验结果采用常用的聚类评价指标[24]准确率(Acc)、调整兰德指数(ARI)、调整互信息(AMI)、标准化互信息(NMI)以及迭代次数(Iterations)来进行评价.

ARI常用于聚类算法的评估,它的前身是兰德系数(Rand Index, RI).计算RI值需要数据集的真实标签信息.假设数据集的真实标签为U,聚类后的预测标签为V.则将a表示为在U和V中为同一类的数据对象的对数.b表示为在U中为同一类,在V中属于不同类的数据对象的对数.c表示为在U中为不同类,但在V中属于同类的数据对象的对数.d表示为在U和V中属于不同类的数据对象的对数.则RI的计算公式为:

(27)

其中,RI的取值范围在[0,1]区间内,RI值越大,算法的聚类效果越好.RI的问题在于对于两个随机的划分,不能保证使RI值接近于0.基于此提出ARI[25].计算公式为:

(28)

其中,ARI在[-1,1]范围内取值,ARI取值越接近1,表明算法的聚类质量越好.

AMI是对互信息(Mutual Information, MI)的一种改进.MI取值范围为[0,1],但是对于随机结果,不能保证MI值接近0.为解决这一问题,提出AMI能更好地反映数据分布,计算公式为:

(29)

其中,H(U)为样本对象的边缘熵值,E|MI|为互信息的期望值.AMI取值范围为[-1,1],AMI取值越大说明算法的聚类结果越好.

NMI[26]取值范围为[0,1],NMI取值越大说明算法的聚类结果越好.计算公式为:

(30)

4.3 实验结果分析

7个二维人工数据集选自不同形状、不同规模、不同簇数和不同稀疏程度的常用人工数据集.其中Aggregation[27]包含7个不同大小的簇,部分簇有轻微连接.Flame[28]两个簇具有不同的大小和形状,且其中一个簇被另一个簇半包围.4K2_far是一个经典的4类数据集.D31[29]具有高达31个簇,包含3100个样本.G2_2_30是一个高斯聚类数据集,具有不同的聚类重叠和维度.Jain两个簇为月牙形状,且两个簇密度不一致,上月牙较为稀疏,下月牙较为稠密,是具有不规则形状的经典数据集.R15[29]将600个样本划分为15个簇,其中一个簇位于空间中心,被7个簇紧密包围.图3展示了本文提出的ANNDP算法寻找初始类簇中心的效果.虽然在Aggregation数据集中有个别簇的聚类中心定位到了簇边缘,但是由于后续模糊聚类算法仍需继续迭代优化聚类中心,因此只要ANNDP算法能准确将初始聚类中心定位到每个簇中就会取得不错的聚类效果.由实验结果可以得知ANNDP算法在整个寻找初始聚类中心过程中根据数据集局部的稠密情况自适应的寻找近邻样本集合,且仅需让近邻样本参与计算,降低了计算量,在不同数据集中能将初始聚类中心准确的定位到每个簇中.

图3 ANNDP算法在不同数据集上搜索初始聚类中心结果Fig.3 Result of ANNDP algorithm searching the initial clustering centers on different datasets

在7个真实数据集上用上述提到的5个评价指标进行了对比实验.表3展示了ANNDP-WFCM算法和其他5种算法在每个数据集上5个评价指标的实验结果.在Seeds、SPECT、Haberman、Bupa、Leuk72_3k数据集上5个评价指标均取得了最好的效果,其中,在Iris、SPECT、Haberman和Bupa数据集上相比于其他5种算法准确率有较大幅度的提升.虽然在Wine数据集中AMI和NMI两个指标略低于KDPC-FCM算法,但是Acc、ARI和迭代次数均好于其他5种算法.在迭代次数的比较上本文提出的算法略优于同样提前获取初始聚类中心的FDP-FCM算法和KDPC-FCM算法,远远优于其他3种算法.通过实验结果可以发现,本文提出的算法,整体上优于其他5种模糊聚类算法,尤其是结合自适应近邻和密度峰值的思想引入了初始聚类中心,基于信息熵赋权区分不同特征的重要程度.不仅使聚类准确率有一个较好的提升,同时使迭代次数显著降低,加速了模糊聚类算法的收敛.使其能够更快更好的迭代到最优值.为更直观的描述本文算法和其他3种算法的比较结果.图4采用折线图直观描绘了不同的数据集、不同算法在同一评价指标上的比较结果.

5 结 论

本文针对传统FCM算法的聚类结果容易受到随机选取初始聚类中心的影响,且在聚类过程中忽视了样本的不同特征和样本本身的重要程度对聚类结果产生的影响.提出了一种结合自适应近邻与密度峰值思想的基于信息熵加权的模糊聚类算法(ANNDP-WFCM).在7个选自不同形状、不同规模、不同簇数和不同稀疏程度的常用二维人工数据集上可视化了本文提出的ANNDP算法寻找初始聚类中心的能力.在7个常用真实数据集上验证本文提出的ANNDP-WFCM算法和FCM算法、FWCM算法、NW-FCM算法、FDP-FCM算法、KDPC-FCM算法相比,在聚类准确性和减少迭代次数上具有一定的优势.但是,FCM算法通过迭代寻优,容易陷入局部最优,本文在这个问题上尚未进行优化,因此后续工作将围绕提高模糊聚类算法的全局优化能力开展研究,从而进一步提高模糊聚类算法的性能.