结合APF和改进DDQN的动态环境机器人路径规划方法

孙传禹,张 雷,辛 山,刘 悦

(北京建筑大学 电气与信息工程学院,北京 100044)

1 引 言

目前机器人开始被广泛应用于医疗、救援、军事、太空等领域.在这些领域中,机器人所处的工作环境是复杂、动态和非结构化的场景.现有经典全局路径规划算法如人工势场法、快速探索随机树法等,需要已知环境的先验信息.并存在计算量大、通用性差及无法适应动态应用场景等难题.基于反应式的局部导航方法,如神经网络、强化学习算法等,则不需要已知环境的先验信息,可以自主学习提升规划策略,与经典算法相比具有优越性[1],可以应用于复杂的、动态的、地图残缺的场景中,但存在缺乏随机探索能力,学习效率较低,收敛速度较慢等问题.

为了改善上述方法,人们采用先由全局规划算法获取初始环境信息,再由局部路径规划算法实时获取复杂场景的障碍物信息的方法,以增强算法的稳定性.Van Hasselt等人[2]提出一种深度双重Q网络的算法以解决DQN算法存在的过估计问题.董永峰等人[3]提出动态目标双深Q网络算法,将DDQN与平均DQN结合,缓解DDQN在路径规划中价值低估的问题.Oscar等人[4]提出改进人工势场法并应用于动态环境下的有源滤波器避障分析.U Orozco等人[5]将Bacterial-Potential field技术引入人工势场法,提高了人工势场法路径规划器的性能.但基于人工势场的改进算法在实时环境中移动避障依然存在性能相对较差和较容易陷入局部最优陷阱的问题.深度强化学习算法(Deep Reinforcement Learning,DRL)的提出使得强化学习技术在现实场景中的复杂问题中具有良好的性能和鲁棒性[6].Oualid等人[7]提出一种DRL改进算法,使配备激光测距仪的微型飞行器系统能够在没有GPS的环境中自主导航,缓解了DRL路径规划算法计算消耗大的问题.Huang R等人[8]提出了一种改进DQN算法,解决了动态障碍物与移动机器人之间因为相对运动引起异常奖励,导致移动机器人与动态障碍物之间的碰撞的问题,但算法的收敛速率较慢.Yao Q等人[9]将改进人工势场法与DQN结合缓解了环境中存在多个目标位置造成的势场重叠,机器人易陷入局部最优陷阱的问题,但实验在动态环境中效果没有得到验证.Chiang H等人[10]通过结合基于抽样的规划、快速探索的随机树和DRL,提出了一种动态运动规划的有效解决方案,但存在复杂环境中效率较低的问题.

DRL方法中基于DQN路径规划算法是利用不同的状态-动作对作为神经网络的输入,以Q函数值作为输出.神经网络每一次更新,目标Q网络都会采取最大化操作,这样的操作会导致动作值偏高,出现过估计的问题,移动机器人可能会陷入局部最优陷阱,收敛速度较慢.DDQN通过改进DQN神经网络结构可以有效解决DQN过估计问题[11],但它在选择动作时,是利用当前估计网络参数,而不是利用不断更新的先验知识,所以会造成价值低估的问题.在传统DQN路径规划算法中,移动机器人的状态集为当前位置相邻的四个状态,这使得算法规划的每一个步长路径之间存在直角夹角,平滑度较差.

传统人工势场方法可以快速获取路径,但存在以下3个不足之处[12]:1)当机器人距离目标位置较远时,机器人所受引力较大,斥力相对较小,容易撞上环境中的障碍物;2)当目标位置附近存在障碍物时,机器人移动至目标位置附近时,所受引力较小而斥力相对较大,容易导致机器人无法到达目标位置;3)当机器人在环境中某一位置所受引力和斥力恰好相等,例如机器人当前位置、障碍物位置与目标位置处于一条直线时,容易导致局部震荡或者陷入局部最优陷阱.

针对上述传统DQN和人工势场路径规划算法的问题,本文将DRL强大的学习能力和对未知环境的处理能力与人工势场快速获得路径的特点结合,提出了一种基于人工势场法和改进深度双重Q网络路径规划算法PF-IDDQN.将人工势场法中的势能引入到DDQN奖励模块中,缓解DDQN中奖励稀疏问题,使得学习器的探索更具目的性,减少盲目探索,降低DDQN因动态障碍物移动陷入局部最优陷阱的概率.同时人工势场法中由于引力与斥力合力为零导致局部最优陷阱时,DDQN算法的随机探索策略可以让学习器尝试不同的路径,有效缓解人工势场的不足.

本文主要工作如下:首先,对移动机器人所在环境中的静态障碍物和动态障碍物人工势场进行建模,构建势能地图.其次,将势能地图引入DDQN算法中,将不同状态的势能差作为DDQN算法的密集奖励,同时对移动机器人的状态集进行了优化,增加了4个状态;最后,移动机器人在动态环境中进行训练仿真,对比传统DRL算法,验证提出算法的性能.实验结果表明,该算法不仅可以在具有动态障碍物的环境中快速推导出路径提升算法成功率,缓解了DDQN算法收敛缓慢的问题,而且可以解决人工势场方法中存在的局部最优解的问题.

2 方法描述

2.1 人工势场法

人工势场(APF)方法是一种全局路径规划算法,通过在环境中构建虚拟势场的路径规划方法[13].势场由两种位场组成:重力场和斥力场.目标物对主体施加重力,形成重力势场,引导机器人向目标位置移动.同时,障碍物产生脉冲力,形成排斥势场,引导机器人躲避障碍物[14].在人工势场中,势能受重力场和排斥场的影响.障碍物附近位置的势能较高,而目标附近位置的势能较低,如图1所示.因此,在排斥势场和引力势场合力的驱动下,移动机器人从高势能位置移动到低势能位置,同时找到一条能够到达目标位置的无碰撞路径.地图上目标位置的引力(即重力)覆盖了整个环境地图,因此移动机器人可以从地图上的任何位置向目标位置移动[15].

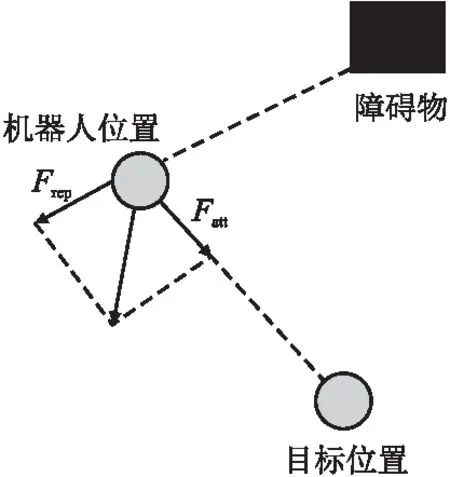
图1 人工势场中机器人受力分析Fig.1 Force analysis of robot in artificial potential field

人工势场法机器人受力分析如图1所示.2D空间的引力场示意图如图2所示.

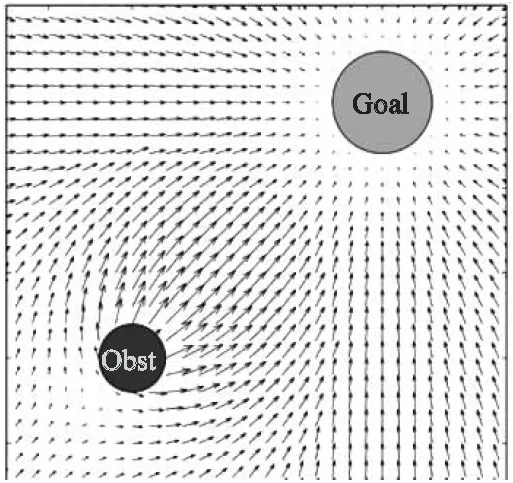
图2 2D空间引力场[16]Fig.2 Gravitational field in 2D space[16]

传统的引力场函数如下:

(1)

其中η是尺度因子,d(q,qgoal)是机器人当前位置与目标位置的距离.目标位置对机器人的引力为引力场对距离的导数:

Fatt(q)=-Uatt(q)=ζ(qgoat-q)

(2)

传统的斥力场函数如公式(3)所示:

(3)

其中η是斥力因子,d(q,qobs)是机器人到距离机器人最近的障碍物的欧几里得距离,d0是每个障碍物的影响半径.当机器人和障碍物的距离大于障碍物影响半径时,机器人不受障碍物影响.

斥力场产生的斥力为:

Frep(q)=

(4)

总势场为斥力场与引力场的叠加,机器人所受合力为对应分力的叠加.

U(q)=Uatt(q)+Urep(q)

(5)

F(q)=-U(q)

(6)

2.2 强化学习

在强化学习中,学习器在不同时间步中将与实验环境交互.在实验中,每一个时间步内学习器都将接收一个状态st,同时根据实验中的策略π如随机策略等,从动作集合A中选择一个动作at.策略π是学习器从当前状态到选择的动作的影射.学习器执行动作at并进入到下一个状态st′,得到一个奖励rt作为st的反馈.Rt是从当前位置开始到一次训练或测试结束所得到的奖励的折扣累积,Rt计算公式如公式(7)所示:

(7)

其中γ是折扣因子,设置折扣因子的目的是弱化远期状态对现在状态的影响,越近的状态对当前状态影响越大.学习器的最终目标是最大化每个状态的期望累积奖励.

动作值函数是描述学习器在不同状态一直根据策略π选择动作a,直到一次训练或测试结束得到期望奖励,如公式(8)所示:

Qπ(s,a)=E[Rt|st=s,at=a,π]

(8)

值函数定义为:

Vπ(s)=E[Rt|st]

(9)

对于环境中所有状态的集合S,如果一个策略π的期望回报大于或等于其他策略的期望回报,那么该策略为最优策略π＊,定义为:

(10)

如果当前状态的下一个状态st′已知所有动作的Q值函数,那么π*可以选择最大化期望回报的动作.

(11)

2.3 DQN算法及DDQN算法

Mnih等人[17]将卷积神经网络与传统的Q-learning算法结合,提出了DQN算法模型,该模型的提出开创了深度强化学习新的研究领域.DQN的训练更新流程如图3所示.

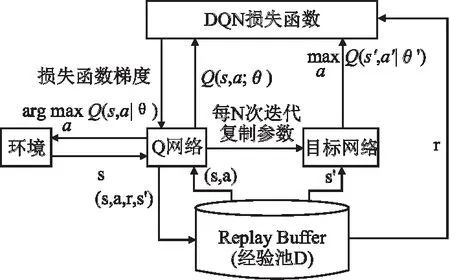
图3 DQN训练更新流程Fig.3 DQN training update process

DQN算法使用了固定Q目标的方法,即采用了两个网络,在神经网络学习时通过网络来估算Q的真实值,通过网络W对参数进行优化,当满足规定迭代次数后用网络W来更新网络W-,这样将Q的真实值和预测值区分开,减少实验结果振荡.

针对非线性神经网络表示值函数的稳定性较差等问题,DQN算法主要对传统的Q-learning算法做了2处改进[6].

1)DQN算法引入两个卷积神经网络分别用来近似表示当前的状态值函数和产生目标值函数Q值.DQN在每次迭代i中优化损失函数如公式(12)所示:

Li(θi)=Es,a,r,s′[(Yt-Q(s,a|θi))2]

(12)

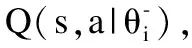
(13)

当前状态值函数网络的权值θ是实时更新的,每经过N轮迭代,算法将当前状态值函数网络的参数复制传递给目标值函数网络.初始化时,θ=θ-.DQN通过最小化当前状态Q值和目标状态Q值之间的均方误差来更新神经网络参数.如公式(14)所示:

L(θt)=Es,a,r,s′[Yt-q(s,a|θt))2]

(14)

DQN算法引入了目标函数值网络,目标Q值在N次迭代时间内是保持不变的,有效降低了当前状态Q值和目标状态Q值之间的关联性,相较于传统Q-learning算法提升了算法的稳定性.

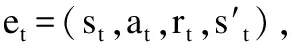
Li(θi)E(s,a,r,s′)～U(D)[(Yt-Q(s,a|θi))2]

(15)

深度学习训练神经网络时,通常要求训练样本相互独立.DQN算法通过随机采样的方式,显著降低了训练样本之间的关联性,从而提升了算法的稳定性.

DDQN算法与DQN算法相同,具有两个Q网络结构,同时也具备经验回放机制.不同点在于DDQN在传统DQN算法的基础上,通过当前正在更新的Q网络的参数选择最优动作,来缓解传统DQN算法过度估计的问题.DDQN计算目标Q值的方法如公式(16)所示:

(16)

3 基于人工势场法和改进深度Q网络路径规划算法

本文假设移动机器人在[0,90],[0,60]的长方形实验空间中,空间中有4个边长为10的静态障碍物,6个边长为1的动态随机障碍物.人工势场法是全局路径规划算法,本文首先对实验环境中的障碍物、目标位置势场进行建模构建势场地图;然后基于势场地图定义强化学习奖励模块;最后训练Agent在动态环境中躲避障碍物并移动到目标位置.

3.1 环境势场建模

基于传统人工势场方法对移动机器人实验空间中的引力势场和斥力势场进行了建模.目标位置的引力势场计算方法如公式(1)所示.

建立所有静态和动态障碍物位置的斥力势场模型,障碍物的斥力势场计算方法如公式(3)所示.

在机器人的环境中,目标位置处的势场值最小,距离目标位置较远的势场值较大.在障碍物附近的势场中,越靠近障碍物,势场值越大.

3.2 基于势场的强化学习定义

本文提出的算法根据上述势场模型定义了强化学习中的动作空间、状态空间和奖励函数.本文将强化学习中的动作定义为机器人的当前位置与下一个位置之间的距离差值.这个动作是一个二维连续矢量,其中二维分别表示机器人沿x轴和y轴的位移.针对传统DDQN算法中规划的路径平滑度较差的问题,本文将机器人的动作空间,增加左前、右前、左后及右后方向4个方向[12],机器人可以向8个方向移动.动作空间改进后,机器人可移动方向示意图如图4所示.

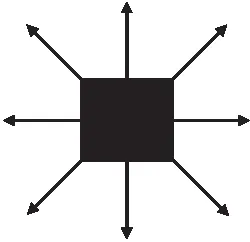
图4 改进DQN算法动作集示意图Fig.4 Schematic diagram of the action set of the improved DQN algorithm

势能地图中每一个已知点都有其对应的二维坐标,所以实验模型的状态空间S可以表示为:

S={(x,y)|0≤x≤W,0≤y≤H}

(17)

其中W为势能地图的宽度,H为势能地图的高度.

在路径规划问题中,本文希望机器人每一次移动都尽可能接近目标位置,并且尽可能远离障碍物影响范围.因此,本文将算法奖励进行如下定义:根据势能地图中每个状态的势能值,计算当前状态与下一状态的势能差值即为该动作的奖励值;目标位置的奖励应为较大值.当出现如下情况时机器人结束一次训练或测试:

1)机器人移动100个步长未到达目标位置;

2)机器人触碰障碍物或者地图边界;

3)机器人移动到目标位置

将相邻两个状态的势能差值作为RL的密集奖励,可以有效缓解DDQN算法奖励稀疏的问题,加快算法收敛的速度,减少Agent的无效探索.本文设置100个步长内到达目标位置作为算法的一个性能指标,传统离散RL算法采用随机策略探索环境空间,算法往往需要付出大量的步长去探索未知空间和移动到目标位置,本文算法在训练和测试过程中可以使用较少的步长到达目标位置,性能相比传统DRL算法有很大的提升.RL是一种试错的算法,但在实际生活中,机器人试错的成本非常高,在本文仿真中,本文设计机器人如果与障碍物或环境空间边界发生碰撞,该轮训练或测试结束,尽可能避免机器人在训练或现实测试时与障碍物发生碰撞.

3.3 算法流程

根据DDQN算法中神经网络的训练流程,本文设计了基于人工势场法和改进DDQN算法神经网络一次更新流程图,如图5所示,其中Batchsize为算法进行一次训练所需的样本数量.本文提出算法中,使用ε-greedy作为探索策略,为了算法更好更快的收敛,同时提升Agent实验后期探索效率,探索率ε初始值较大,但随着迭代次数的增加而逐渐变小.

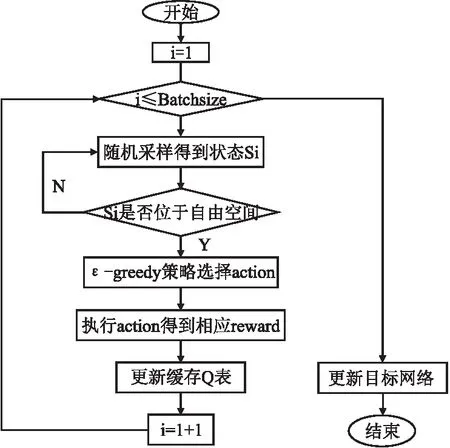
图5 算法一次训练更新流程图Fig.5 Algorithm for one-time training update flowchart

本文提出改进算法框架图如图6所示,首先,对环境地图进行采集获取State,将采集的地图转化为势能地图;其次,将获取的势能地图引入DDQN网络中;最后,通过得到的价值函数Q进行动作选择,将动作反馈给环境,得到奖励R,将R反馈给DDQN网络进行迭代更新.

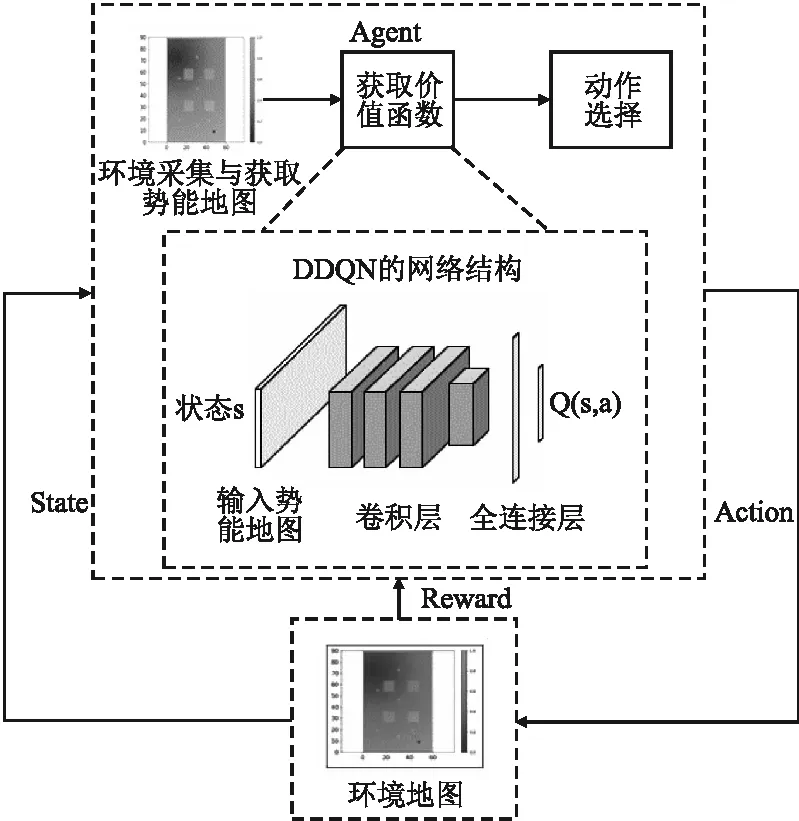
图6 本文提出算法网络框架图Fig.6 This paper proposes the algorithm network framework diagram

本文提出的算法流程如算法所示:

算法.基于人工势场和DDQN路径规划算法

输入：环境信息及算法参数

输出：Q网络参数信息

a)初始化经验池D,初始化Q目标网络参数和当前网络参数容量为N,初始化所有状态及动作的值

b)for episode=1 M T

c)初始化实验环境状态,根据环境中的机器人位置、目标位置和障碍物位置,计算环境位置势能,根据计算的势能得出总的势能地图

d)通过总的势能地图,机器人根据当前位置周围5X5的环境势能,选择势能最小的最优动作

e)得到机器人执行动作 后的奖励 和下一个网络的输入s′,同时将机器人获取的环境特征信息(s,a,r,s′)保存到经验池D中(经验池中的记忆矩阵保存着前N个时刻的状态)

f)随机从经验池D 中取出n个样本,按照公式(9)对Q值进行更新,并将更新后的Q值作为目标值,计算样本中每一个状态的目标值

g)使用均方差损失函数,通过神经网络的梯度反向传播来更新Q网络的所有参数

h)每C次迭代后更新目标网络参数

i)如果下一状态是障碍物、地图边界或目标位置,当前轮迭代完毕,否则转到步骤d)

j)end for.

4 仿真实验及结果分析

本文实验环境为CPU AMD 锐龙5 5600X,Pytorch 1.10对DDQN网络进行训练.本文移动机器人仿真实验采用全局路径规划算法与局部路径规划算法结合的方式.实验中,首先构建全局势场地图,构建的势场地图如图7所示,Agent每移动一个步长,势能地图将更新一次,定位动态障碍物的位置.

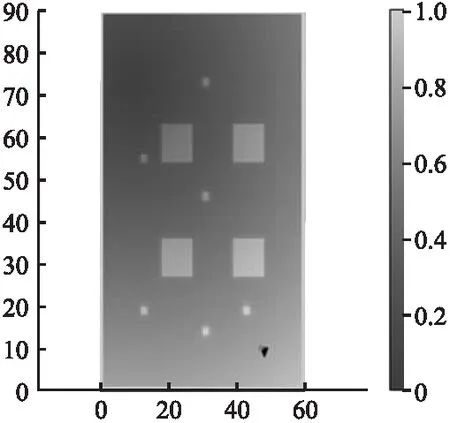
图7 实验环境势场地图Fig.7 Potential field map of the experimental environment

其中4个大正方形为静态障碍物,6个小正方形为动态障碍物,动态障碍物在20×20范围内随机移动.起始位置在地图右下角,目标位置在地图左上角,右下角黑色点为机器人当前位置,地图颜色越深势能越高.本文中势场公式参数的设定为ζ=1,η=20,d0=3.

本文中奖励模块设置参数如表1所示.

在实际实验中,可以使用激光雷达获取实验场景地图如图8所示,再将地图转化为势能地图,在像素地图中,每一个黑色像素点可视为障碍物,Agent每移动两个像素点,更新一次局部势能地图,本文实验中实时更新Agent前方60×60的势能地图,该大小的地图更新造成的延迟对Agent的实际移动的影响可以忽略不计.

图8 激光雷达获取实际环境地图Fig.8 Lidar obtains actual environment map

为验证算法在动态环境中的性能、探索效率以及收敛速度,本文限制移动机器人每次训练最多移动100个步长.实验参数如表2所示.

表2 实验参数Table 2 Experimental parameters

将本文提出的算法与基于改进DQN算法的DDQN算法在相同实验环境中进行实验对比,两种算法每轮训练的奖励值如图9～图10所示.

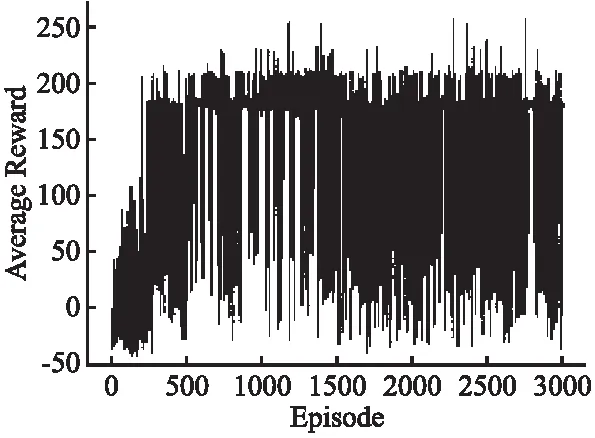
图9 本文提出算法训练中奖励值曲线图Fig.9 In this paper,the curve of reward values in algorithm training is proposed

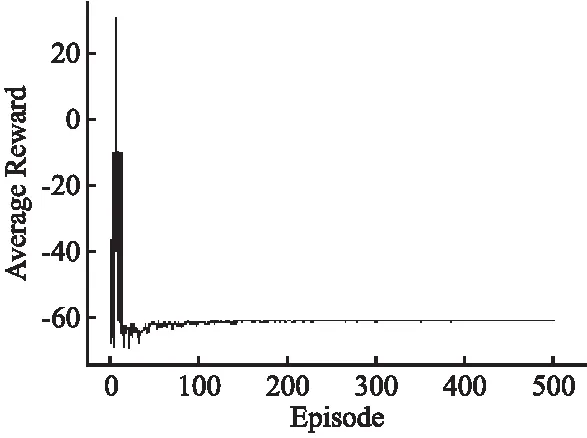
图10 传统DDQN算法训练中奖励值曲线图Fig.10 Reward value curve graph in the training of traditional DDQN algorithms

由图9可以看出本文提出的算法在迭代150次以上得到了170左右的较高的奖励值,算法奖励值集中在150～200区间;而基于传统DDQN算法在限制的探索次数下无法探索到目标位置,在迭代约40次后陷入了局部最优陷阱或无法越过动态障碍物,由图10可以看出该算法在陷入局部最优陷阱后的奖励值趋于相似值,故实验只进行了500次迭代.

本文实验中,有3条结束本次训练或测试的条件,由图11～图12可知,当移动次数小于60时机器人可能与障碍物或地图边界发生碰撞;当移动次数大于60小于100时,可认为机器人有较高概率成功到达目标位置;当移动次数为100时,可认为机器人有较高概率受到动态障碍物影响未能在规定移动次数内到达目标位置.本文提出的算法在机器人移动60～70个步长收敛.

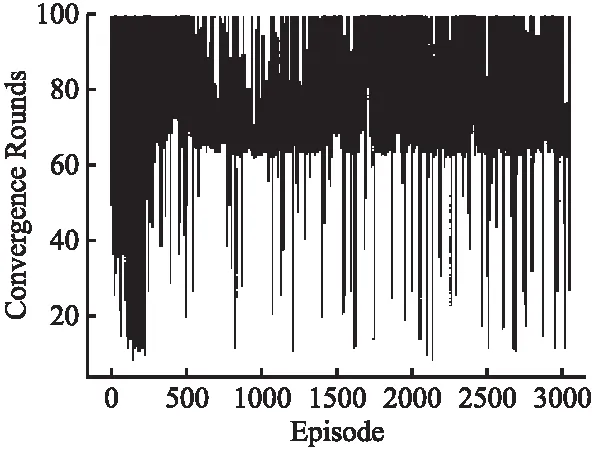
图11 基于人工势场和改进DQN算法收敛回合Fig.11 Convergence round based on artificial potential field and improved DQN algorithm

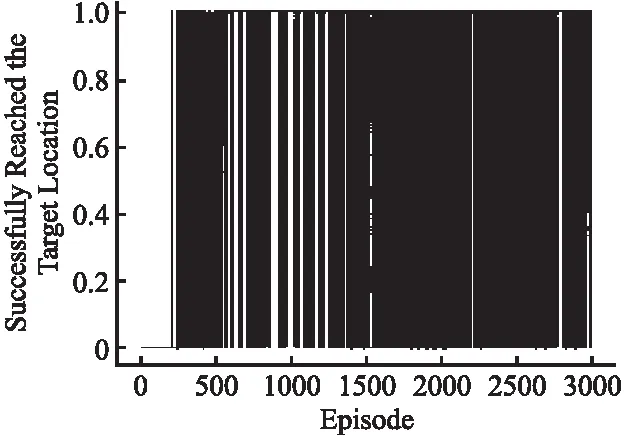
图12 训练中机器人成功到达目标位置Fig.12 Robot successfully reached the target position during training

如图11所示,基于人工势场和改进DDQN算法在3000次训练迭代中,移动机器人在约150次迭代后路径规划成功率在89%以上,基于传统DDQN算法无法规划出到达目标位置的路径.

移动机器人在实验环境中测试的效果如图13所示.可以看出,实验中移动机器人在遇到左下角静态障碍物时,出现了呈Z字型移动,这是由于奖励模块总是驱动移动机器人向目标位置移动,即总是相左上方移动,但在实验中,为降低移动机器人与障碍物的碰撞,本文设计移动机器人与障碍物保持一定距离,所以出现上述现象;虽然在实验中移动机器人在遇到动态障碍物时,会额外付出一定步长寻找通行路径,但本文提出算法依旧可以规划出通往目标位置的路径.在实验300次测试中,移动机器人在规定移动次数内路径规划成功率在97%以上.

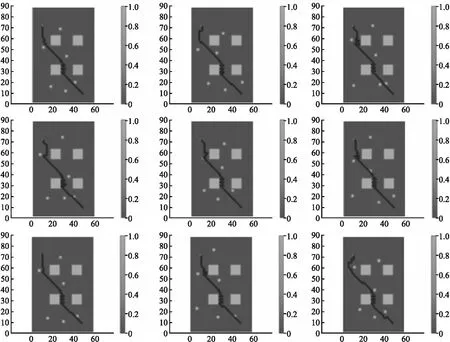
图13 机器人在静态及动态障碍物环境中测试结果Fig.13 Test results of the robot in static and dynamic obstacle environments

5 结 语

本文提出的基于人工势场法和改进DDQN算法可以应用于动态实验环境,算法中值函数的估计更加准确,移动机器人可以在有限移动次数下快速地识别出相对最优的动作,收敛速度更快.本文采用DDQN算法更新Q值,缓解了Q值估计过高的问题.引入人工势场缓解了DQN算法奖励稀疏的问题,加快了算法网络收敛的速度,提高了移动机器人在动态环境路径规划的成功率.综上所述,本文提出的算法可以利用更少的移动次数在较少迭代次数内得到更大的奖励值,从而使得移动机器人可以在更短时间内更准确的获得最优路径.