面向三维模型的尺寸标注完备性检查算法

燕 哲 董玉德 何金鑫 贵兴锋 陶高周

1.合肥工业大学机械工程学院,合肥,2300092.阳光电源有限公司中央研究院,合肥,230088

0 引言

三维标注技术日趋成熟,已逐渐被应用于零件的设计流程。现有的三维标注系统多以组合视图为基础,通过对标注进行分类管理来解决“刺猬现象”,这导致三维尺寸完备性检验更为复杂。尺寸标注的完备性检验就是检查零件模型是否存在冗余尺寸、是否缺失尺寸。零件越复杂,尺寸标注的数目越多,人工检查的难度就越大[1-4],因此,国内外众多学者对三维尺寸标注的完备性检验进行了相关研究。

尤炎炎等[5-6]对尺寸数据进行预处理,构建关于尺寸节点的邻接矩阵,再以该邻接矩阵进行尺寸冗余和缺失判断。罗磊等[7]提出一种基于参数化建模映射关系的尺寸完备性检验算法,以牛顿迭代法求解映射矩阵,以化简后的映射矩阵进行完备性分析。无论是创建邻接矩阵还是映射矩阵,当模型复杂导致特征过多时,矩阵的阶数会变大,使计算过程缓慢甚至难以实现完备性检验。

程亚龙等[8-11]引入定位元的概念,提出一种基于刚性体识别的三维尺寸完备性检验方法,将循环约束问题转化为刚性体的识别问题。刘金锋等[12-13]提出基于尺寸标注元素优先级的定形尺寸规范化处理方法和基于特征约束的定位尺寸完备性检验方法。但这两种思路均未考虑三维尺寸中可能出现的等价尺寸情况,尺寸的冗余性判断不够完整。

付超凡等[14-15]基于集合约束传播进行尺寸完备性检验,以几何要素约束模型,并以尺寸信息模型为主要数据得到尺寸冗余和尺寸缺失信息。康杰等[16]通过模糊聚类学习,对标注结果进行结构约束和完备性检测。这两种检验方法无法实现尺寸链冗余情况的判断。

综上所述,目前众多学者关于三维标注完备性检验还存在以下不足:①大部分检验算法只适用于简单零件,当模型复杂时,尤其是基于特征矩阵实现完备性检验的算法,其效率极低;②冗余性检验未能实现对等价冗余尺寸和尺寸链冗余两种情况的完全检验;③目前所有完备性检验算法均在标注完成后进行,但若在标注过程中进行冗余性检验,标注效率更高。

因此,本文提出等价尺寸集和等价节点的概念;基于自研三维标注系统,在尺寸创建过程中实现三维尺寸的冗余性检验;基于面特征的完全约束判断,将尺寸缺失检查转换为面特征约束检查。

1 等价尺寸相关概念介绍

1.1 等价尺寸与等价尺寸集

三维标注过程中会出现多个标注表示同一约束的情况,降低了三维标注的可阅读性和严谨性,因此,本文定义表示同一约束的尺寸互为等价尺寸,它构成的集合为等价尺寸集。下面分析每一种类型尺寸可能存在的等价尺寸。

1.1.1直线类型尺寸

当创建尺寸的几何元素只包含一条直线时,创建类型一定为距离尺寸。如图1所示,L1为选中的一条直线,对于以L1为参考所创建的距离尺寸,存在的等价类型(集合中所有元素应与L1相邻)包括直线-直线{L2-L3,L4-L5,…}、直线{L6,L7,…}、平面-平面{S1-S2,…}、直线-平面{L2-S2,L3-S1,…}。

(1)直线-直线:以L2-L3为例,判断L2、L3是否均垂直于L1,若满足则判断L1、L2、L3是否共面。

图1 直线

(2)直线:以L6为例,判断L6是否为L2、L3除L1以外的另一个公共邻近边,若满足则判断L6是否与L1平行且等长。

(3)平面-平面:以S1-S2为例,判断S1、S2是否均垂直于L1。

(4)直线-平面:以L2-S2为例,判断L2、S2是否均垂直于L1。

1.1.2直线-直线类型尺寸

当创建尺寸的几何元素包含两条直线时,如图2所示,创建类型可能为距离尺寸或角度尺寸(排除两直线异面的非法情况)。求解该类型尺寸的等价尺寸,需先判断两直线是否有重合的邻近面,若没有则不存在等价尺寸集。

图2 直线-直线

当直线-直线平行时,如图2中L2-L3,创建类型为距离尺寸,存在的等价类型(集合中所有元素应与L2或L3相邻)包括直线{L1,L6,L7,…}、面-面{S1-S2,…}、直线-平面{L2-S2,L3-S1,…}。

(1)直线:以L1为例,判断L1是否在S3上,若满足则判断L1与L2是否垂直。

(2)平面-平面:以S1-S2为例,判断S1、S2的法向量是否均与L2的方向向量垂直。

(3)直线-平面:以L2-S2为例,判断S1-S2是否等价于L2-L3,若满足则判断L2的方向向量与S2的法向量是否垂直。

当直线-直线相交时,如图2中L2-L6,创建类型为角度尺寸,存在的等价类型(集合中所有元素应与L2或L6相邻)包括平面-平面{S1-S5,…}、直线-平面{L2-S5,L6-S1,…}。

(1)平面-平面:以S1-S5为例,判断S1、S5的夹角是否与L2和L6的夹角相同。

(2)直线-平面:以L2-S5为例,判断S1-S5是否等价于L2-L6,若满足则判断L2、S5的夹角是否与L2、L6的夹角相同。

1.1.3直线-平面类型尺寸

当创建尺寸的几何元素包含一条直线和一个平面时,如图3所示,创建类型可能为距离尺寸或角度尺寸。

图3 直线-平面

当直线-平面平行时,如图3中L2-S2,为距离尺寸,存在的等价类型(集合中所有元素应与L2或S2相邻)包括直线-直线{L2-L3,…}、平面-平面{S1-S2,…}。

(1)直线-直线:以L2-L3为例,判断L2、L3是否平行,若满足则判断L2到L3的距离是否与L2到S2的距离相同。

(2)平面-平面:以S1-S2为例,判断S1、S2是否平行,若满足则判断S1到S2的距离是否与L2到S2的距离相同。

当直线-平面相交时,如图3中L1-S1,创建类型为角度尺寸,存在的等价类型(集合中所有元素应与L1或S1相邻)包括直线-直线{L1-L2,L1-L4,…}、平面-平面{S1-S4,…}。

(1)直线-直线:以L1-L4为例,判断L4是否属于S1,若满足则判断L1、L4的夹角是否与L1、S1的夹角相同。

(2)平面-平面:以S1-S4为例,判断S4是否包含L1,若满足则判断S1、S4的夹角是否与L1、S1的夹角相等。

1.1.4平面-平面类型尺寸

当创建尺寸的几何元素包含两个平面时,如图4所示,创建类型可能为距离尺寸或角度尺寸。

图4 平面-平面

当平面-平面平行时,如图4中S1-S2,创建类型为距离尺寸,存在的等价类型(集合中所有元素应与S1或S2相邻)包括直线-直线{L2-L3,L4-L5,…}、直线{L1,L6,…}、直线-平面{L2-S2,L3-S1,…}。

(1)直线-直线:以L2-L3为例,判断L2、L3是否有公共的邻近面S3,若满足则判断L2、L3是否平行。

(2)直线:以L1为例,判断L2-L3或L4-L5是否等价于S1-S2,若满足则判断L1是否在L2、L3的重合面S3上且L1是否垂直于L2。

(3)直线-平面:以L2-S2为例,判断L2是否与S2平行。

当平面-平面相交时,如图4中S1-S3,创建类型为角度尺寸,存在的等价类型(集合中所有元素应与S1或S3相邻)包括直线-直线{L1-L4,…}、直线-平面{L1-S1,L4-S3,…}。

(1)直线-直线:以L1-L4为例,判断L1、L4是否有公共的邻近面S4,若满足则判断L1、L4的夹角是否与S1、S3的夹角相等。

(2)直线-平面:以L1-S1为例,判断L1、S1的夹角是否与S1、S3的夹角相等。

1.1.5圆弧类型尺寸

当创建尺寸的几何元素包含圆弧时,如图5所示,可能的创建类型包含圆弧(如arc1)、圆弧-平面(如arc1-S1)、圆弧-直线(如arc1-L1)、圆弧-圆弧(如arc1-arc2),上述尺寸的等价尺寸集仅包含本身。

1.2 等价节点

三维标注的尺寸链冗余检验存在尺寸链中节点不重合的问题,因此,本文将某一等价尺寸集中所有尺寸两端元素分别抽象为两个节点,进行信息存储,并定义该节点为等价节点。

一条尺寸链由若干距离型尺寸构成,主要有直线、直线-直线、直线-平面、平面-平面、圆弧-圆弧、圆弧-直线、圆弧-平面。上述距离型尺寸均由两端几何元素进行约束,约束元素包括点、直线、平面、圆弧。如图6所示,将元素集合{P1,P2,P3,P4,L1,L2,L3,L4,S1}抽象为节点N2,集合{P′1,P′2,P′3,P′4,L′1,L′2,L′3,L′4,S′1}抽象为节点N1。

图6 等价节点

图7 尺寸冗余性检验

2 尺寸冗余性检验

尺寸冗余检验的逻辑如图7所示。首先判断该尺寸的创建是否会造成等价尺寸冗余,若不存在等价尺寸,则判断是否会导致尺寸链冗余,若尺寸创建未导致尺寸链冗余,则说明该尺寸非冗余。

2.1 基于等价尺寸集检验冗余尺寸

基于等价尺寸集进行冗余尺寸检验的逻辑如图8所示。首先获得创建尺寸所需几何元素集中所有元素的标识号,并求得对应key值。判断该key值是否已经存在,若存在则说明该尺寸为等价冗余尺寸,若不存在则进行等价尺寸集创建。

本文基于迭代思想创建等价尺寸集。首先将创建尺寸的初始几何元素集加入栈中,然后每次获得栈顶的几何元素集并出栈。以集合中所有元素的标识号获得对应key值。若key值存在则进行下一次判断,否则记录key值并判断该几何元素集是否属于直线、直线-直线、直线-平面、平面-平面中的一种,若属于则执行上述等价尺寸的判断逻辑,找出该尺寸对应的所有等价尺寸的几何元素集并压入栈中。

2.2 基于等价节点检验尺寸链冗余

图9a为一轴类零件三维标注的示意图。基于上述等价节点的概念,将图9a中的标注约束元素抽象为若干等价节点集合,并按标注间的约束关系构建图9b所示的无向图。

基于无向图进行尺寸链的冗余检验,其检验逻辑如图10所示。首先获得尺寸两端约束所属节点N1、N2,然后基于深度遍历算法查找等价节点构成的无向图中以N1为起点的所有路径,判断是否存在经过N2的路径,若存在则该尺寸的创建会导致N1与N2形成闭环,即尺寸链冗余。

3 尺寸缺失检验

尺寸标注的目的是对模型中所有面特征进行约束,因此,三维标注的尺寸缺失检验可以转换为查找模型中未能完全约束的面特征。模型中需约束的面特征包括平面、圆柱面、圆锥面。

(a)标注示意图

(b)无向图图9 等价节点构建无向图

图10 尺寸链冗余性检验

对平面而言,通过判断该平面是否属于某个等价节点来判断是否已被约束。如图11a所示,完全约束一个圆柱面,需要约束圆柱的高和半径。高为距离尺寸,可以判断是否存在某等价尺寸集包含以下尺寸:arc1-arc2、S1-S2、arc1-S2、arc2-S1。圆柱半径是否被约束只需判断是否有某等价尺寸集包含arc1或arc2。若高和半径均被约束,则该圆柱面被完全约束。如图11b所示,完全约束一个圆锥面,相比于圆柱面需再判断其是否已被标注锥度尺寸,即锥角是否被约束。

(a)圆柱面

(b)圆锥面图11 约束判断

尺寸缺失检验的逻辑如图12所示。首先,基于深度遍历算法获得模型所有面特征,然后根据每个面特征的类型逐个判断该面是否已被完全约束,若未被完全约束则将该面特征高亮显示。

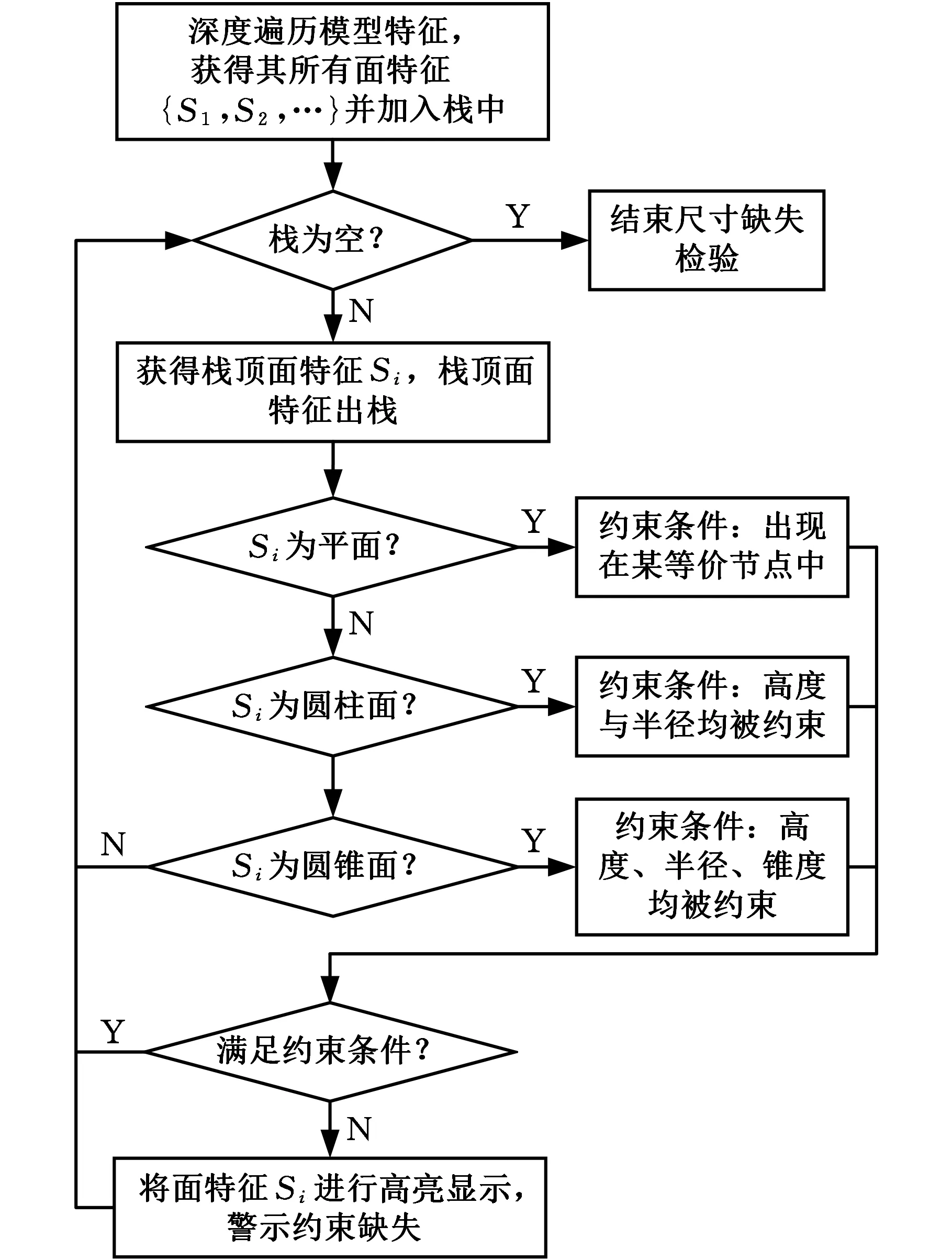
图12 尺寸缺失检验

4 实例分析

目前,国内外学者研究的三维标注系统多以对话框的嵌套调用实现,且未包含尺寸完备性检验功能,导致三维标注的效率较低[17-19]。如图13所示,本文三维标注系统以仪表盘为框架进行设计,避免了对话框的冗余嵌套带来效率损失。本文设计了两个版本的三维标注系统,如表1所示。“原系统”未包含尺寸完备性检验功能,“改进系统”中实现了本文所提出的尺寸完备性检验算法。对某装配体中具有不同特征的多个零件模型进行测试,测试结果表明,在标注过程中执行尺寸冗余性检查能够提高标注的整体效率。由表1可知,改进系统标注效率最高提高了25%,最低提高17%。因为模型越复杂在标注过程中出现尺寸冗余的可能性越大,则效率提高也就越多。

图13 标注示例

表1 标注效率对比表

如图13所示,对“8ld_287_1003_model_.prt”零件在标注系统中基于尺寸功能进行标注。为提高标注的可阅读性,以“视图1”、“视图2”两个组合视图对标注进行分类管理。“视图1”的标注效果如图13所示,“视图2”的标注效果如图14所示,此时零件的多个面特征已被约束。

(a)等价尺寸冗余

如图14所示,对该零件进行尺寸冗余创建测试,图中高亮几何元素为创建尺寸所选元素。图14a所示为等价尺寸冗余,此时创建尺寸所选元素集已存在于某等价尺寸集中,因此程序判断为等价尺寸冗余,并弹出对话框提醒。图14b所示为尺寸链冗余,此时创建尺寸所选两元素对应等价节点间已存在一条路径,因此程序判断为尺寸链冗余。

如图15所示,对该零件进行尺寸缺失检验。程序对零件中所有面特征进行约束检验,将其中未被完全约束的面特征高亮显示,并弹出对话框指出未被约束的面特征个数及其标识号。

由测试结果可看出,本文算法能够在尺寸创建过程中避免等价尺寸冗余和尺寸链冗余;在标注完成后,可进行尺寸缺失检验,对缺失约束的面特征进行高亮提示。检验结果正确,验证了该算法的正确性和有效性。

5 结语

(1)提出等价尺寸集与等价节点的概念,以等价节点构建无向图替代邻接矩阵,可实现对复杂模型的完备性检验。

(2)基于CREO软件中的自研三维标注系统实现了在尺寸标注过程中进行等价尺寸冗余和尺寸链冗余的检验,相比于标注完成后检验,效率明显提高。

(3)提出各类型面特征的约束判断条件,将尺寸缺失检验转化为面特征约束检验。实例测试结果表明,该算法能够正确检查出三维尺寸标注存在的尺寸冗余和尺寸缺失。

(4)目前,本文算法未能实现对螺纹、齿轮等由标准参数形成的特征以及样条曲面特征的尺寸缺失判断。由于各类螺纹的标注组成不同,故需对不同类型螺纹执行不同逻辑的尺寸缺失检验;齿轮特征需结合模型本身标注及齿轮参数表进行尺寸缺失的判断;样条曲面特征的尺寸缺失检验需对放样点距离约束、每段曲线的曲率以及角度约束进行综合判断。由此可见,这些方面有待进一步研究。