基于改进梯度下降算法优化的磁梯度张量组合不变量算法的管道缺陷边缘识别模型
邢海燕 弋 鸣 段成凯 王学增 刘伟男 刘 传
1.东北石油大学机械科学与工程学院,大庆,1633182.中国石油大庆石化分公司,大庆,163000
0 引言
石油和天然气在能源体系中具有战略地位,其运输总量中管道运输占80%~90%[1]。随着管道的长期运行,腐蚀、磨损等缺陷导致的管道泄漏事故频发,对经济发展和生态环境造成严重破坏[2]。在管道运行过程中早期隐性损伤往往难以精确定位,因此对管道缺陷进行边缘识别十分必要。
在役管道常用超声、涡流、漏磁等方法检测缺陷,但这些方法只能检测宏观缺陷,与之相比,金属磁记忆技术不仅能检测宏观缺陷,而且可以检测早期应力集中及隐性损伤[3-4]。ZHAO等[5]通过X80管线钢脉动冲击疲劳试验,确定磁记忆特征参数能反映疲劳损伤状态的变化;王贵生等[6]基于支持向量机方法对磁记忆信号特征进行分析,建立了管道缺陷的分类、分级识别模型;罗同顺等[7]利用模糊判据,实现了对污水管道缺陷的等级评价;陈海龙等[8-9]提出了磁梯度张量水平模量和梯度局部波数,实现了板状试件裂纹的特征提取。
目前,研究人员在管道磁记忆检测方面进行了大量研究,但检测结果受检测方向影响大、缺陷边缘识别困难的问题一直没有得到很好的解决。本文对管道试件的预制缺陷从不同检测方向进行原始磁记忆信号采集,利用所设计的磁梯度张量测量系统,通过提取磁梯度张量第二、第三不变量消除了检测方向对磁记忆信号数据的影响。进一步优化第二、第三不变量,利用改进梯度下降算法分别确定最优权值并进行叠加,建立基于磁梯度张量组合不变量算法的缺陷边缘磁记忆识别模型,实现管道缺陷边缘精准识别。
1 问题描述
实际工程中,管道的走向多种多样,当沿管道检测方向与地磁场方向的夹角不同时,磁记忆信号会发生变化,影响检测结果的可靠性[10]。
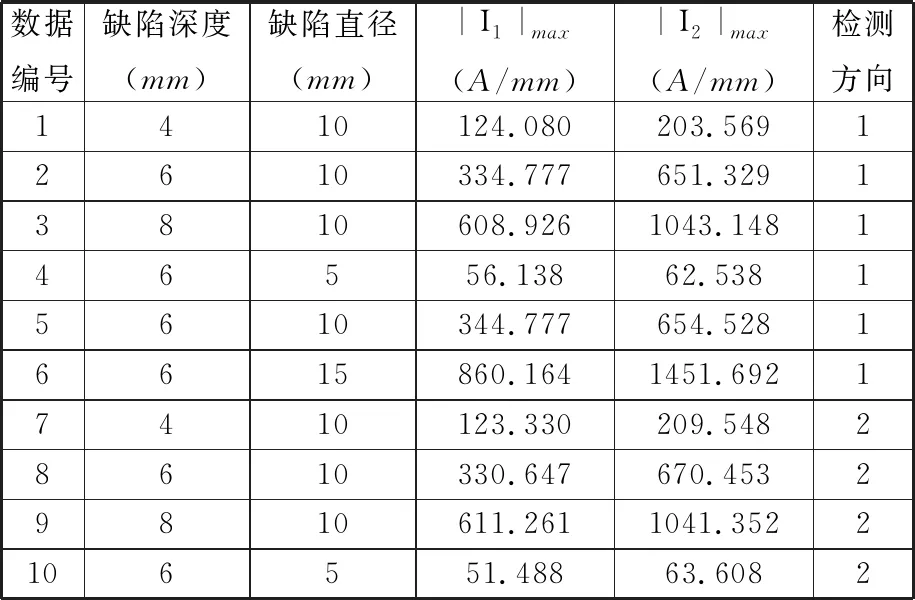
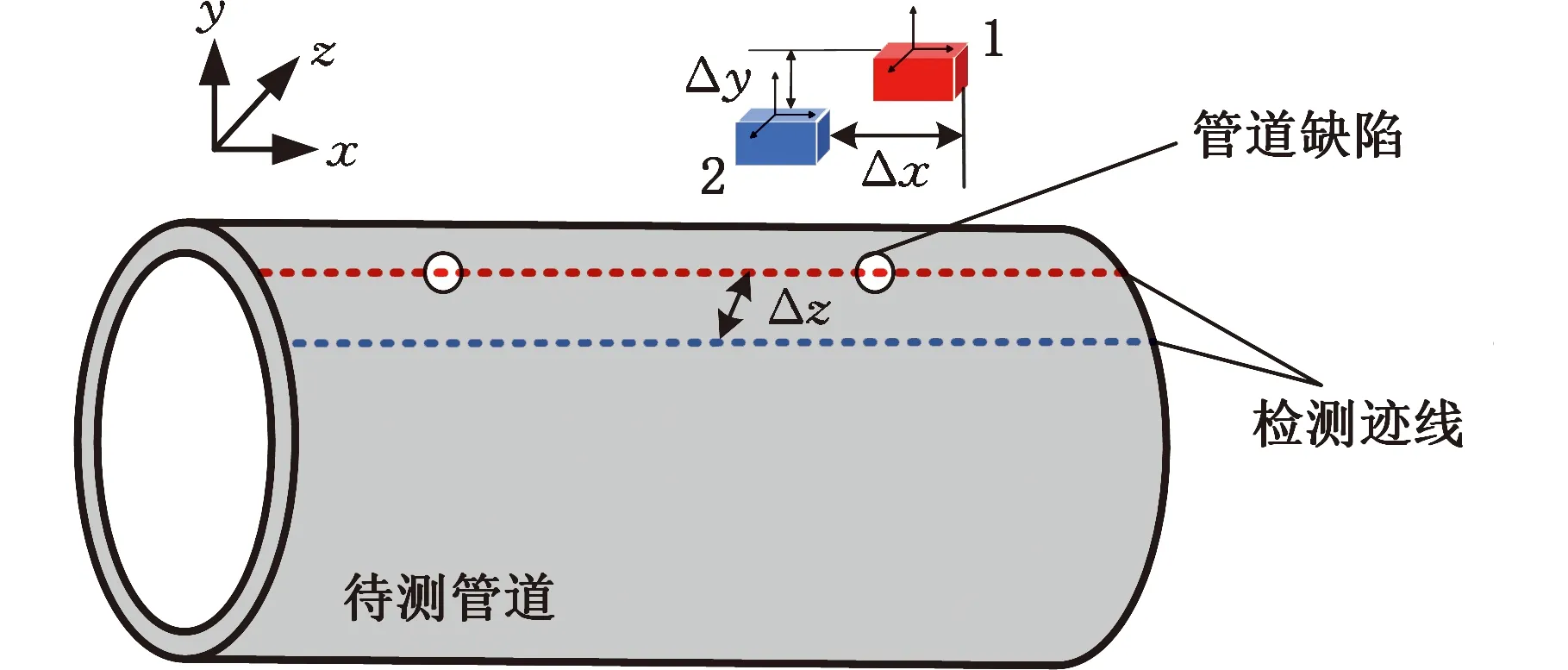
以图1所示实验管道试件为例,具体阐述检测方向不同对磁记忆信号的影响。管道试件材质为L245N管线钢,直径为340 mm,壁厚为10 mm。预制孔状缺陷以模拟管道常见的点蚀,其中:1、2、3号缺陷直径均为10 mm,深度依次为4,6,8 mm;4、5、6号缺陷深度均为6 mm,直径依次为5,10,15 mm。采用俄罗斯TSC-5M-32型应力集中磁检测仪,搭配11-6W型高灵敏度传感器,沿图1所示不同检测方向1、2、3、4分别进行磁记忆信号扫描。
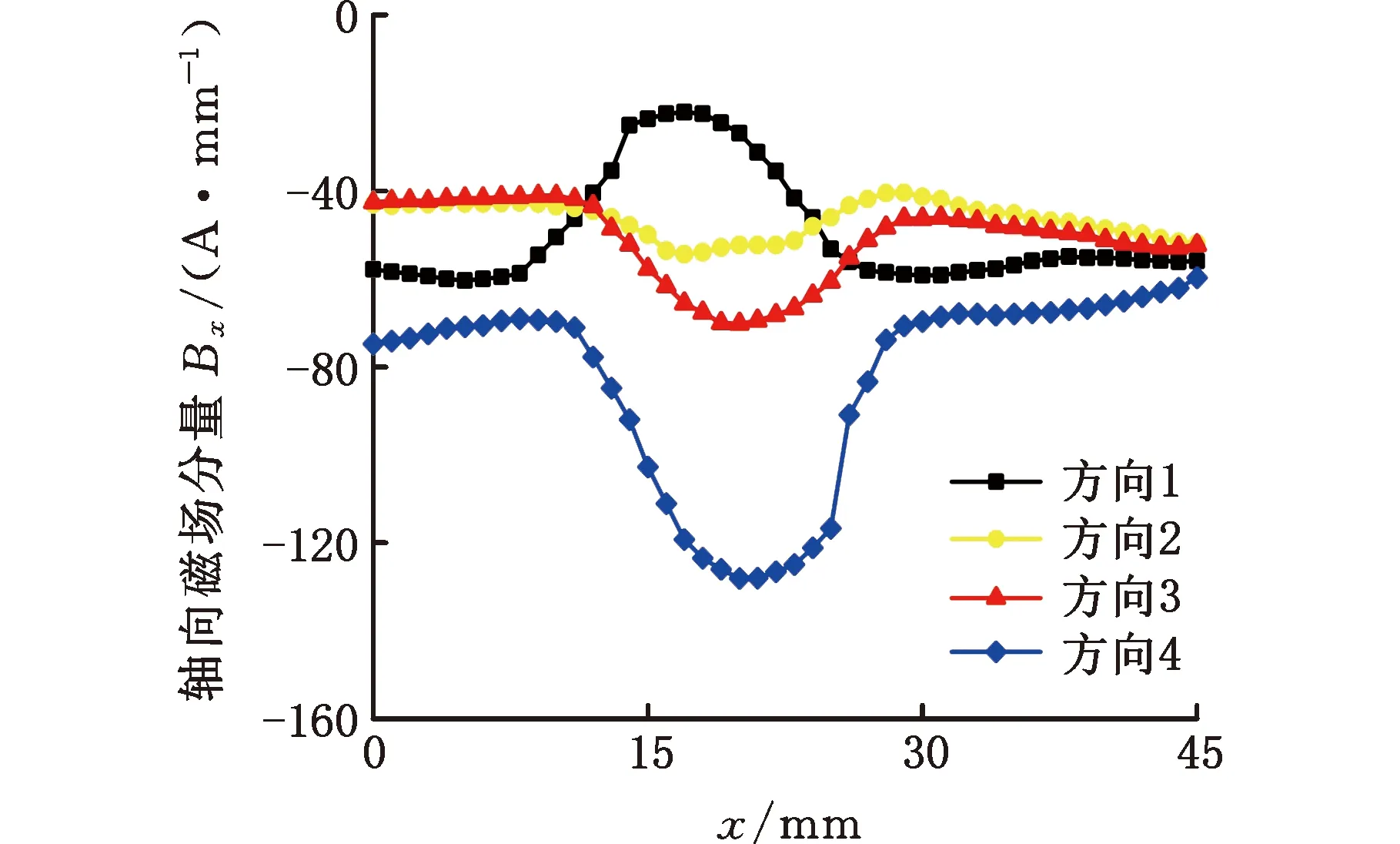
(a)轴向磁场分量Bx
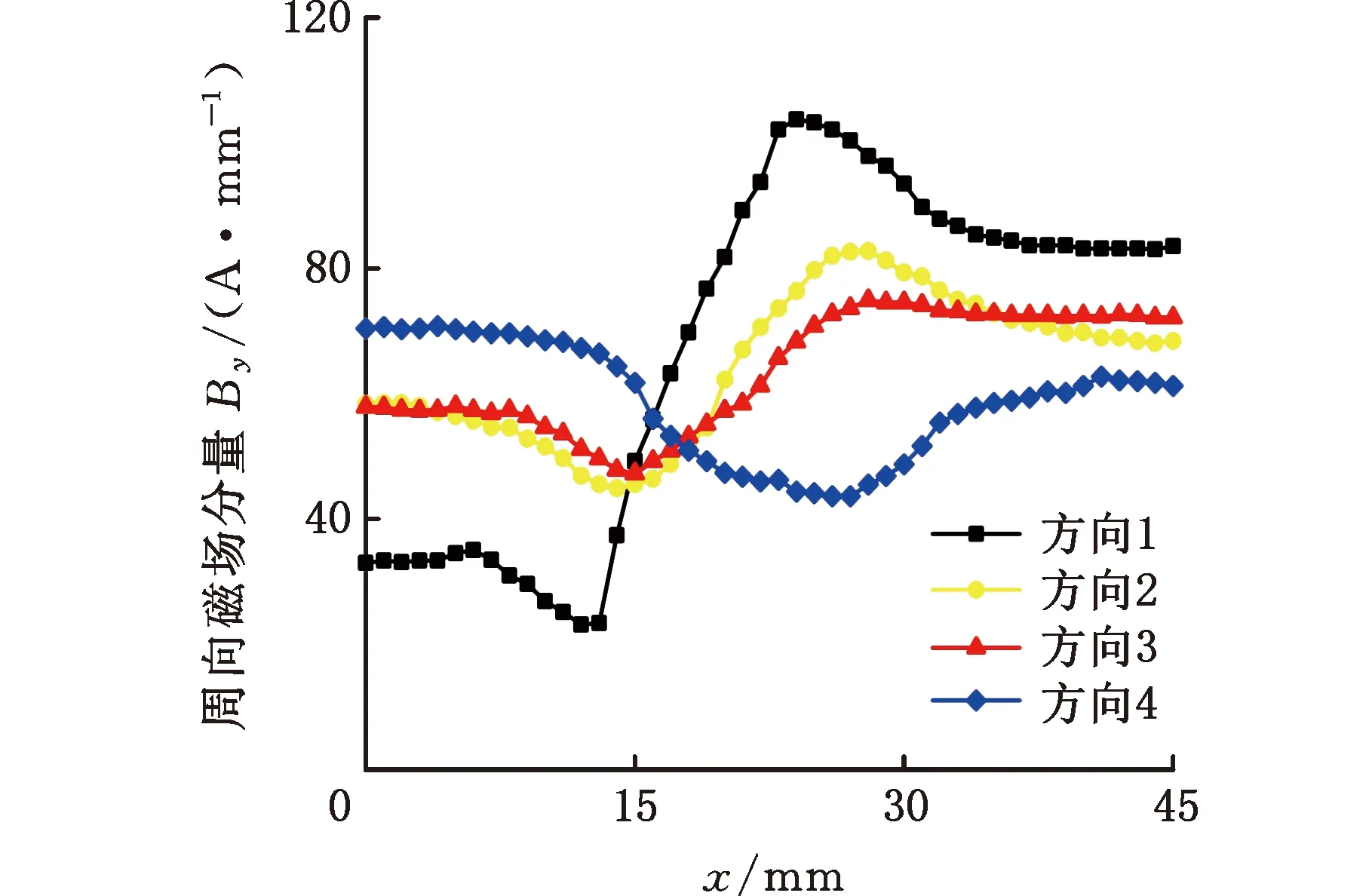
(b)周向磁场分量By
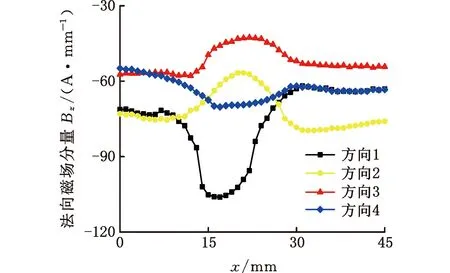
(c)法向磁场分量Bz图2 φ5 mm×6 mm缺陷不同方向的磁场分量
同一缺陷在不同检测方向上磁记忆扫描信号差别非常大,现以4号缺陷为例进行详细说明,图2为不同检测方向上磁场分量对比图,其中Bx为沿管道轴向、By为沿管道周向、Bz为沿管道法向的磁场分量。由图2a可以看出,同一缺陷的Bx在方向1上为正跳变,而方向2、3、4均为负跳变,跳变幅值、跳变点位置无规律可循,因此直接利用磁记忆原始数据无法进行缺陷边缘精准识别,且检测方向对检测结果的影响严重。
2 磁梯度张量组合不变量理论
磁梯度张量理论常应用于资源勘探、军事、环境领域[11],可以实现磁源目标的定位和边界识别。PEDERSEN等[12]提出了张量模、特征值及特征向量等磁异常表征方法;在此基础上,张恒磊等[13]等将磁梯度张量测量方法引入到地质勘探中,提出了基于磁梯度张量的边界探测方法,但对弱异常探测能力有局限性;MAJID等[14]、张朝阳等[15]基于磁梯度张量模实现了磁性物体的识别,但不能反映小尺寸物体的位置。考虑到磁梯度张量受环境磁场影响小,本文将其引入铁磁管道缺陷边缘识别,同时利用磁梯度组合不变量解决弱异常下小尺寸缺陷边缘精确识别的难题。
2.1 磁梯度张量
磁场是个矢量场,在三维空间中,磁场在x、y、z三个方向上的磁感应强度分量的变化率构成一个2阶张量,即为磁梯度张量,记为G,表示为
(1)
地球表面电磁场的传导电流密度及位移电流密度均为零,故其散度和旋度均为零,即为无旋场和无散场,根据Maxwell方程组,可得到磁梯度张量各个分量之间的关系:
Bxy=ByxBxz=BzxByz=Bzy
Bzz=-Bxx-Byy
则式(1)可化简为
(2)
2.2 磁梯度张量不变量
由于磁梯度张量不变量可以很大程度上克服地磁场等背景磁场的影响[16],且不易受测量方向误差的影响,因此本文对磁梯度张量不变量进行提取。磁梯度张量矩阵为实对称矩阵,对其进行对角化处理可得
(3)
式中,λ1、λ2、λ3为磁梯度张量G的3个特征值;v1、v2、v3为特征值对应的特征向量。
由式(3)求得
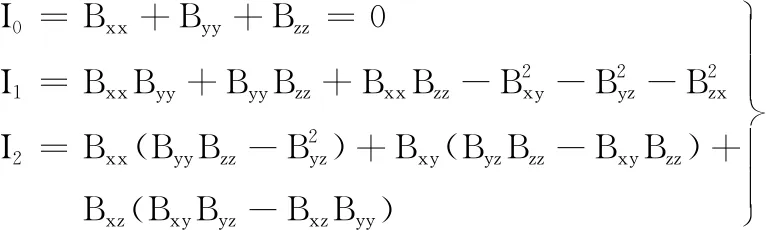
(4)
式中,I0、I1、I2分别为磁梯度张量第一、第二、第三不变量。
2.3 磁梯度张量组合不变量
由实验研究可知,I1、I2两种不变量在缺陷边缘处存在模糊性,故本文提出以张量组合不变量I对I1、I2进行改进。由磁梯度张量矩阵G的特征方程可知:
λ3-I0λ2+I1λ-I2=0
(5)
利用Cardano公式,式(5)的三个解为
(6)
得到I′1、I′2,并分别设置权值a、b,将I′1、I′2进行叠加,得到组合不变量I,公式如下:
(7)
为了对权值a、b进行最优化求解,利用改进的梯度下降(modified gradient descent, MGD)算法对a、b进行寻优。
3 基于MGD优化的磁梯度张量组合不变量的缺陷边缘识别模型
3.1 改进的梯度下降算法
考虑式(7)为无约束优化问题,选取梯度下降(gradient descent)算法进行权值寻优。该算法易于实现且结构简单[17],但它的收敛速度却不快。为提高算法收敛效率,本文根据分数阶求导思想,提出改进梯度下降法。
由式(7)得张量组合不变量缺陷边缘识别模型为
I=h(X)=θ0+θ1x1+θ2x2=θTX
(8)
式中,I为因变量;x为自变量;θ0为偏置项;θ1、θ2为权值a、b的倒数;θT为参数组合的转置向量;X为由(x1,x2)组成的特征列向量。
训练模型的过程就是求解最优化的参数θ1、θ2的过程,假设目标函数为模型的1/2均方误差(MSE),则梯度下降法公式为
(9)
式中,θi为所求的第i个参数;ρ为学习率;m为样本个数;n为数据维度。
一个定义在[c,d]上的函数f(t)的α阶Riemann-Liouville分数阶导数[18]定义为
(10)
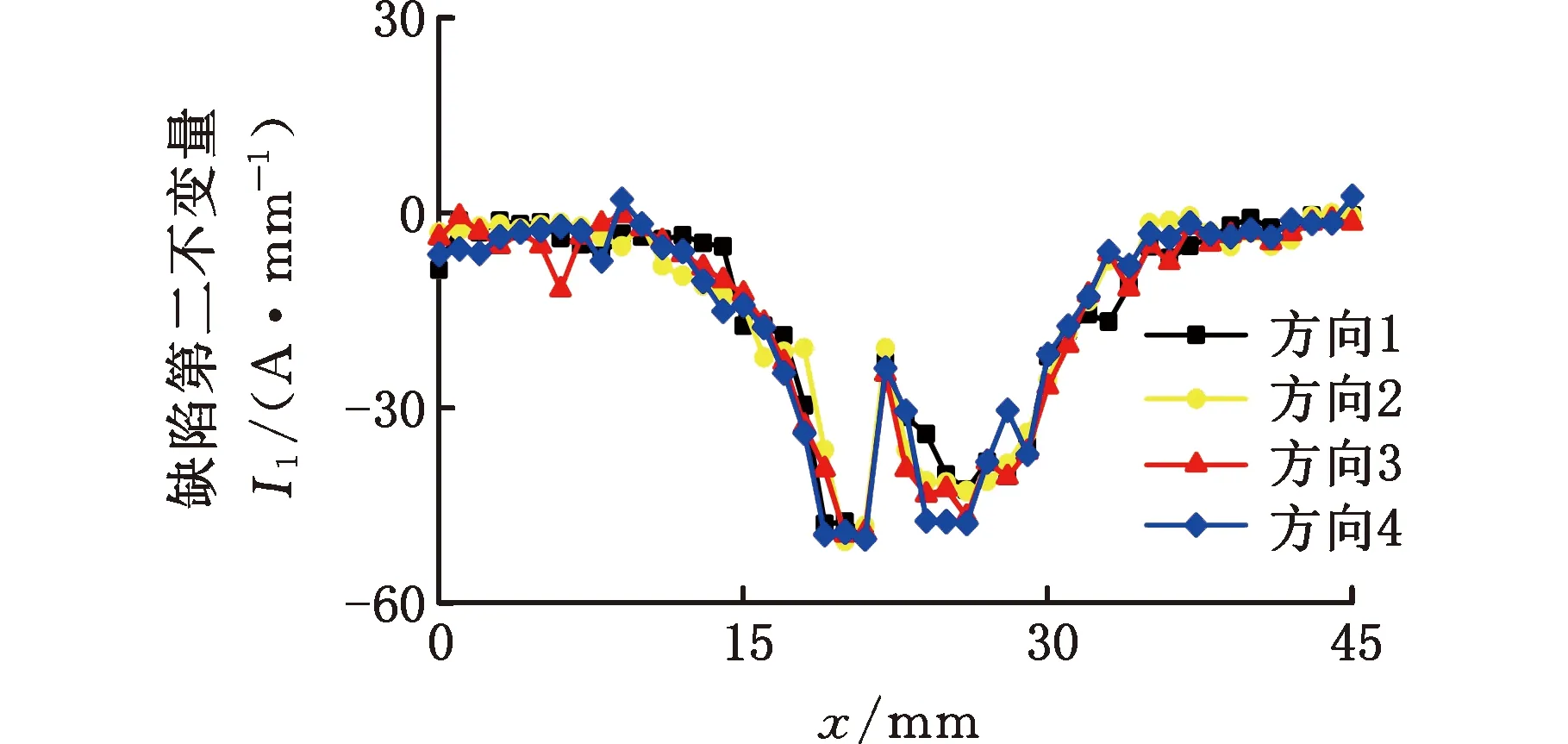
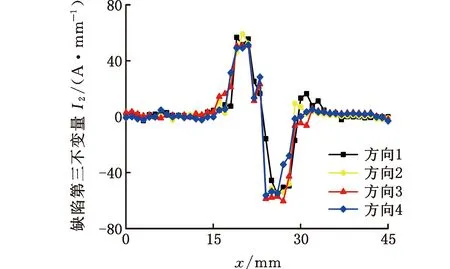
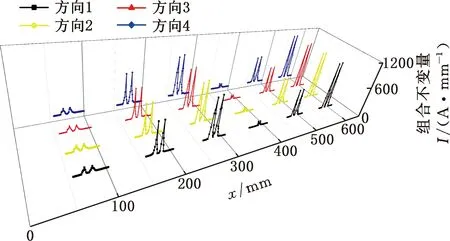
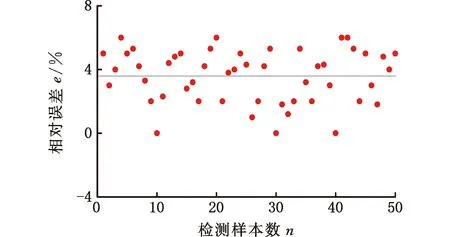
其中,α为大于0小于1的正实数,c≥0,且令g-1≤α (11) 将目标函数代入式(11)得 (12) 分数阶求导可以保证参数都沿着其负梯度的方向移动,使参数更快趋于稳定,提高收敛效率[19]。为提高迭代效率,提高数据优化性价比,根据分数阶梯度的思想对传统梯度下降算法进行改进,得 (13) 本文采用Python软件对模型进行训练和测试,部分原始数据如表1所示,样本输入为I1、I2及检测方向,对I1、I2进行标准化处理,通过梯度下降算法得到最优化权值a、b。标准化处理计算公式为 (14) 设定梯度下降相关参数,代码随机种子均取1,初始模型参数θ0,θ1,θ2=0,学习率ρ取0.001,系数α取0.5,容错ε取0.01。利用改进梯度下降算法找到最优化θ1、θ2值,得到θ1=0.125 83、θ2=0.096 57,代入张量不变量I的计算公式,完成磁梯度张量组合不变量缺陷边缘识别模型的构建。 现有金属磁记忆检测仪无法直接测量缺陷处 表1 部分原始数据 的磁梯度张量,需设计磁梯度张量测量系统来获得完整的磁梯度张量信息。根据磁记忆铁磁传感器平行等间距移动的特点,采用2个三分量磁探测传感器组成的张量测量系统获得磁场信息,传感器布局如图3所示。 图3 传感器分布示意图 图3中1、2分别为三分量磁探测传感器探头,其各敏感轴相互平行,可同时测量3个分量的磁场。假设2个传感器测量的磁场分别为B1、B2,传感器之间三维距离分别为Δx、Δy、Δz,可求得缺陷处x、y、z三个方向上的磁场分量Bx、By、Bz的变化率为 (15) i,j=x、y、z 故磁梯度张量G可表示为 G= (16) 利用4.1节中设计的磁梯度张量测量系统,沿图1所示的不同检测方向对管道不同尺寸缺陷进行磁梯度张量测量。利用式(4)与式(16)计算得到缺陷处磁记忆信号的磁梯度张量第二、第三不变量I1、I2,如图4所示,与图2磁记忆原始信号相比可以看出,不同检测方向上磁记忆信号的张量不变量I1、I2曲线重复性非常好,说明引入I1、I2两种不变量很好地克服了检测方向的影响,但在缺陷局部边缘处仍然存在着不同检测方向上极值点位置的分散性与模糊性,无法准确识别缺陷边缘。 (a)缺陷第二不变量I1 (b)缺陷第三不变量I2图4 φ5 mm×6 mm缺陷不同方向的张量第二、第三不变量 进一步将I1、I2代入式(7)得到组合不变量I,再代入3.2节建立的基于MGD优化的磁梯度张量组合不变量的缺陷边缘识别模型,得到图5a所示的不同检测方向、不同尺寸缺陷的边缘识别结果,可以看出,随着缺陷直径和深度的增加,磁记忆信号的磁梯度张量组合不变量I的极值不断增大,且极值点所在位置与缺陷实际所在位置相差不超过0.5 mm,两极值点间距离近似等于缺陷大小,平均相对误差3.59%,最大相对误差6%,误差分布如图5b所示。实验结果表明:张量组合不变量不受检测方向的影响且缺陷边缘清晰,证明磁梯度张量组合不变量缺陷识别模型具有实际应用价值,为管道缺陷边缘精确识别提供新途径。 (a)实验管道张量组合不变量示意图 (b)相对误差图5 验证结果 (1)提出了基于改进梯度下降法优化的磁梯度张量组合不变量算法的缺陷识别模型,消除了磁记忆检测方向对检测结果的影响,能够对管道缺陷边缘进行精确识别。 (2)利用设计的磁梯度张量测量系统实现了对预制缺陷管道的磁梯度张量信息的检测。 (3)实验结果表明:模型提出的磁梯度张量组合不变量不受检测方向影响,其曲线呈“双驼峰形”,极大值位置与缺陷边缘一一对应,且随着缺陷直径、缺陷深度的增加极大值增大。模型识别的缺陷边缘位置与实际相差不超过0.5mm,平均相对误差为3.59%,最大相对误差为6%,为实际工程中管道缺陷边缘识别提供了新的思路。
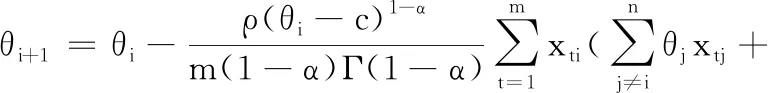
3.2 缺陷边缘识别模型
4 实验研究
4.1 磁梯度张量测量系统设计
4.2 模型的实验验证
5 结论

