滚动轴承接触疲劳裂纹建模与扩展规律研究

郭 伟 曹宏瑞 訾艳阳 尉询楷

1.西安交通大学机械制造系统工程国家重点实验室,西安,7100492.中煤科工西安研究院(集团)有限公司,西安,7100773.北京航空工程技术研究中心,北京,100076

0 引言

滚动轴承被称为“工业的关节”,被广泛应用在能源、重工、运载和国防等领域重大装备中,其工作性能和状态直接影响着设备乃至整体机构的稳定运行。滚动轴承常见的损伤失效方式有裂纹、断裂、磨损、疲劳、塑性变形和腐蚀等,其中轴承的滚动接触疲劳是失效的主要模式之一[1]。滚动接触疲劳按照起始萌生到最终失效的机理通常可分为起源于表面的点蚀和起源于次表面的剥落,次表面疲劳剥落是滚动轴承在具有光滑表面和弹性流体润滑条件下的主要失效模式。断裂力学理论常用于研究裂纹的疲劳扩展行为和扩展机理,而数值模拟方法是研究材料疲劳失效的一种强有力的手段。滚动接触疲劳的研究主要包括轮轨接触、滚动轴承接触和齿轮面接触等几种,国内外许多学者通过数值模拟方法建立滚动接触疲劳裂纹模型,研究不同载荷条件下材料内部应力应变场的变化,同时对材料疲劳损伤裂纹的扩展进行分析和仿真[2-5]。

基于断裂分析的传统有限元方法需要对网格进行重构,计算量较大,同时裂纹只能沿网格边界扩展而不能穿过单元。扩展有限元法(extended finite element method, XFEM)具有不依赖网格划分、裂纹扩展时能够穿过单元和不需要预知扩展路径等优点,可以模拟裂纹的自由扩展路径,在裂纹扩展的研究中逐渐显出了优势。BELYTSCHKO等[6]用附加函数法研究裂纹扩展问题,开启了XFEM的应用。MOЁS等[7]和BUDYN等[8]引入Heaviside跳跃函数,开始将XFEM用于解决不连续性问题。国外对扩展有限元的应用较为广泛,不仅是对各向同性材料进行研究,而且深入到各向异性材料和弹塑性问题,在裂纹扩展、夹杂、孔洞、微结构、接触和多相等不连续问题上都取得了一定的进展[9-11]。国内对扩展有限元的利用开始于2005年,李录贤等[12]第一次全面综述了XFEM的实现和应用。方修君等[13]阐述了XFEM在ABAQUS平台的应用。余天堂[14]模拟了三维裂纹并将XFEM应用到不连续岩体问题中。XFEM在岩土裂纹方面得到了广泛的应用,也证明了其可靠性[15-16]。近年来XFEM理论得到进一步完善和发展,能够满足更复杂工况条件需求,在轨道的轮-轨接触疲劳[17]、齿轮的齿根疲劳裂纹扩展[18-19]、材料裂纹演化机制[20-21]等方面也有一些应用研究,但在滚动轴承方面应用研究仍然较少。

本文建立了包含初始裂纹的滚动接触疲劳扩展有限元模型,模拟了次表面存在初始裂纹时的裂纹扩展路径,研究了初始裂纹的角度、所处深度和裂纹长度对裂纹扩展行为的影响。

1 裂纹扩展理论和XFEM的应用

1.1 裂纹扩展基础理论

载荷作用下,若裂纹尖端塑性变形区相对裂纹长度非常小,则可以采用线弹性断裂力学研究裂纹的演化和失效行为。

1.1.1裂纹尖端应力强度因子计算

对于二维线弹性平面裂纹问题,张开型(Ⅰ型)裂纹的尖端应力场为[22]

(1)

(2)

(3)

式中,KⅠ为Ⅰ型裂纹尖端应力强度因子,表征裂纹尖端的塑性变形程度并判断裂纹发展的趋势,其数值与裂纹长度和载荷有关;a、θ为点的圆柱极坐标,当a和θ趋于0时,裂纹尖端附近点的应力趋于无穷大,即应力的奇异性;f(θ)为量纲一参数。

滑开型(Ⅱ型)开裂模式的应力场方程类似上面的公式,平面无限大板中裂纹倾斜状态下,σxx不产生应力强度因子,而σyy和σxy分别产生Ⅰ型和Ⅱ型开裂模式的应力强度因子KⅠ与KⅡ,可以表示为[18]

(4)

(5)

式中,α为裂纹倾斜角。

1.1.2裂纹的失效准则

实际工程中,复合型裂纹的走向会沿着裂纹分支,而不是原有的裂纹面扩展,裂纹的失效准则目前主要有基于应力的应力强度因子准则、最大拉应力准则、基于能量的最大能量释放率准则以及最小应变能密度准则。其中,应力强度因子准则主要适用于Ⅰ型裂纹的脆性材料,最大拉应力准则的缺点在于其判定断裂只由6个独立应力分量中的1个完全决定,而最小应变能密度准则不适用于压缩情况,因此本文采用最大能量释放率准则[23]。

根据能量守恒定律,裂纹扩展中材料系统内能的增量(包括弹性应变能、新的裂纹面表面能增量和塑性变形功)与外力做功相等。裂纹扩展单位面积时材料内部释放的能量表示为能量释放率G,裂纹扩展单位面积时所消耗的能量临界值表示为GC,当能量释放率G的值大于材料的临界能量值GC时裂纹即开始扩展。

1.2 扩展有限元的应用

扩展有限元是在常规有限元的基础上利用单位分解思想发展而来的。常规有限元的形函数一般是多项式,其应用精度受限于多项式局部逼近。单位分解思想利用局部解作为形函数,使有限元形函数不再受限于多项式[24-25],可以构造自定义的形函数对特定问题进行求解。基于这种思想,扩展有限元引入不连续函数解决不连续问题,改变形函数以实现较好的局部逼近,在位移场中增加带有附加自由度的富集函数,使场变量的逼近函数独立于网格之外,裂纹和计算的网格是各自独立的,因此划分网格时不需要考虑裂纹,裂纹扩展时也不用考虑裂纹尖端变形和网格划分。裂纹可以沿着依赖解的任意路径生长,不需要预定义裂纹的方向和裂纹发展的形状,也不用进行网格重构。由于扩展有限元中的裂纹可以穿过单元,故常用水平集函数分析界面位置并进行跟踪[26-27],并构造形函数描述不连续问题。

ABAQUS软件的XFEM功能模块需要定义裂纹的开裂机制:材料的损伤起始准则用于判断能否使裂纹开裂,对应的是裂纹扩展之前的损伤积累阶段;损伤演化规律用于判断裂纹是否能够形成,对应裂纹开始扩展以后的发展阶段。

ABAQUS有限元软件包含6种材料损伤起始准则,分别为最大主应力准则、最大主应变准则、最大名义应力准则、最大名义应变准则、应力比平方和准则以及应变比平方和准则,其中只有最大主应力准则能够实现裂纹自由扩展,因此本文的计算中采用最大主应力准则,用指标值F衡量损伤是否开始,当F值为1时损伤开始,其表达式为[28]

(6)

材料中损伤积累满足损伤起始准则后,扩展有限元中材料行为即由损伤演化规律决定。损伤演化规律表示的是材料刚度衰退速率,主要有基于位移和基于断裂能这两种演化规律,其中基于断裂能的演化规律通过给出的临界断裂能和相应参数确定单元的演化,本文采用POWER(基于幂法则的断裂能损伤准则)规律。

2 滚动接触疲劳扩展有限元模型的建立

2.1 扩展有限元模型可靠性验证

采用一个简单的单边切口梁的Ⅰ型开裂过程仿真算例验证扩展有限元可以用于仿真材料的开裂。单边切口梁为路面沥青混合材料,数据参考文献[29],模型长376 mm,宽70 mm,梁中间底部预设19 mm初始裂纹。图1是Ⅰ型开裂模式下模型变形图,可以看出,随着载荷施加,在初始裂纹尖端损伤累积到一定程度后,初始裂纹从下向上一步步扩展至整个切口梁从中彻底断开。

图1 Ⅰ型开裂模式下的模型变形示意图

1.裂纹长度变化 2.实验结果 3.模拟结果图2 Ⅰ型开裂模式下P-CMOD曲线和裂纹扩展长度变化

图2所示为计算的载荷-裂纹张开位移(crack mouth opening displacement, CMOD)曲线与文献[29]实验结果的对比,曲线下方包围的面积反映断裂能大小。由图2可见,模拟的结果与实验结果的发展趋势一致,曲线的峰值和曲线包围的面积也比较接近。图中裂纹长度l随裂纹张开位移d的变化趋势与材料断裂过程的基本发展趋势相符。在裂纹尚未扩展时期,材料处于损伤累积状态,载荷峰值也出现在这个阶段;损伤累积达到临界值时,初始裂纹开始扩展;随着裂纹发展,裂纹增长的速度逐渐减慢。图中模拟结果与文献[29]中实验结果吻合较好,说明扩展有限元方法可以很好地用于裂纹扩展的计算。

2.2 滚动接触疲劳扩展有限元模型

以30311圆锥滚子轴承为研究对象,建立二维半无限区域滚动接触模型,模型尺寸为x方向长度10b,y方向深度8b,b为接触半宽,30311圆锥滚子轴承在2 GPa的最大接触应力作用下b=0.1 mm。模型尺寸相比接触半宽b足够大,可以完整体现出Hertz应力场的影响区域,同时可以忽略模型边界应力以及变形的影响。由于计算区域较小,可将滚动接触受力面近似视为一个平面,施加Hertz接触应力,其表达式为[30]

(7)

预设倾斜的、长度为0.02 mm的起始裂纹,模型局部如图3所示。模型划分单元数目8000个,单元类型为平面应变CPE4,最大接触力σmax=2 GPa,忽略摩擦力。模型材料为GCr15,相关参数如表1所示。实际材料中,萌生于次表面的微裂纹尺寸及所处的位置等是随机的,研究不同的起始微裂纹倾斜角度、在材料中的深度和尺寸对疲劳裂纹扩展行为的影响。

图3 裂纹位置示意图

表1 模型中的材料参数

3 结果分析

3.1 疲劳裂纹扩展路径分析

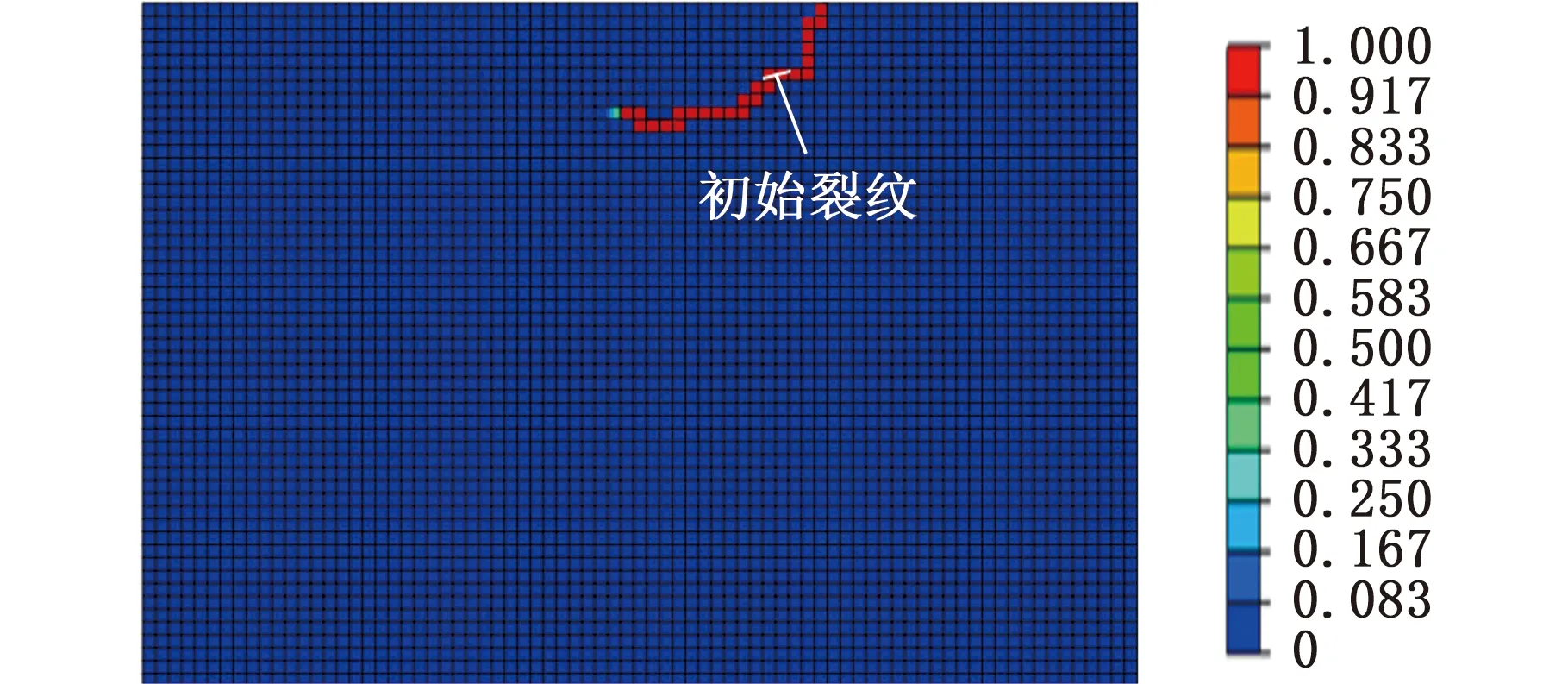
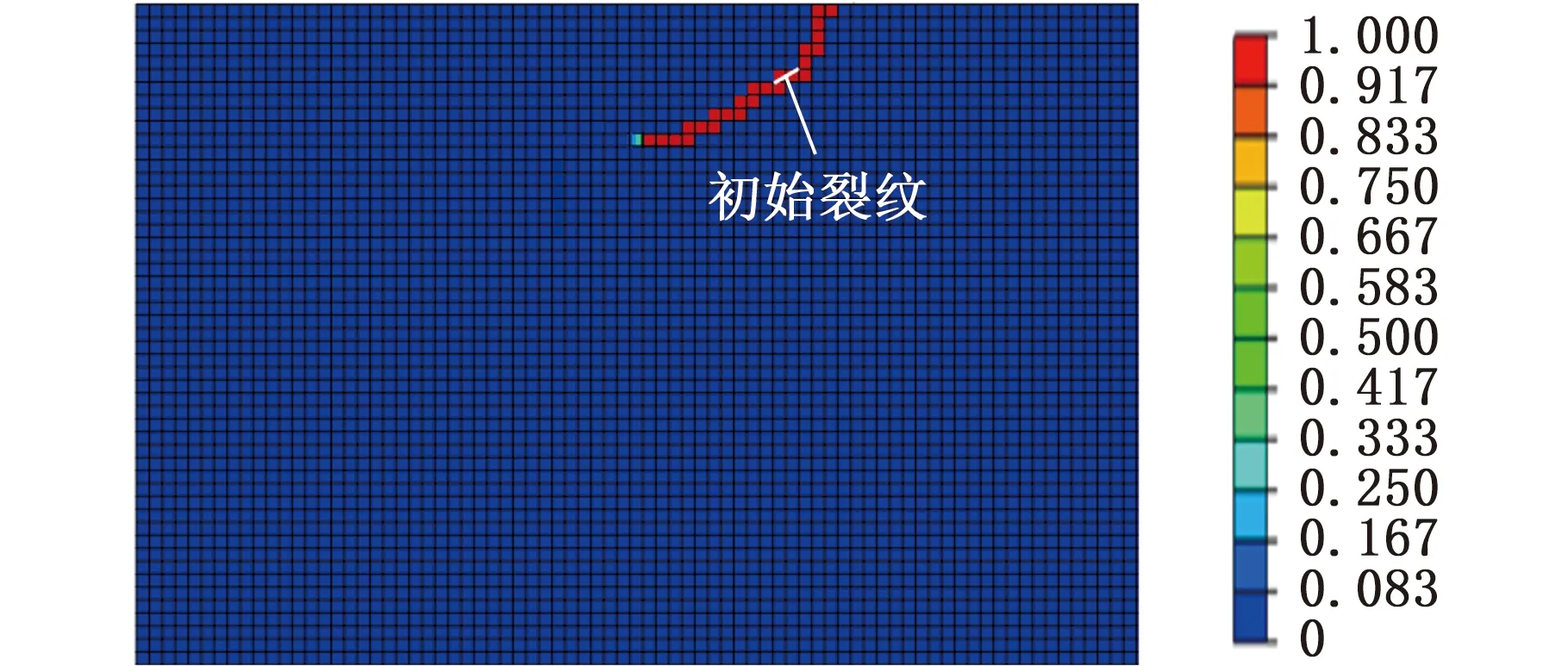
(1)初始裂纹倾斜角度对裂纹扩展路径的影响。保持起始微裂纹长度0.02 mm、所处深度0.05 mm及其余外部条件不变,改变其倾斜角度。以微裂纹靠近表面的一端从初始位置延伸到表面作为疲劳裂纹扩展行为的结束,不同倾斜角度初始裂纹的扩展路径如图4所示。图中刚度衰减结果可以用损伤参数表示,参数为0代表未损伤,1代表完全破坏,此时单元从网格中移除,裂纹向前延伸。由图4可知,不同初始裂纹倾斜角度对裂纹扩展路径的影响比较明显,进而导致最终疲劳剥落区域尺寸出现差异。随着起始裂纹倾斜角度的变大,近表面裂纹尖端的扩展路径与表面之间的夹角变小,倾斜角度在15°和30°时,近表面端扩展路径具有明显的滑开开裂模式特点;而随着角度的增大,裂纹远表面端扩展路径逐渐向材料内部延伸,裂纹倾斜角度在10°～45°时,扩展路径先向基体材料内部延伸再转向表面,但角度越大,裂纹越向材料内部扩展;到初始裂纹角度为60°时,裂纹远表面端没有表现出向表面转向的趋势。这种现象与文献[31]中滚动接触疲劳裂纹扩展路径在扫描电镜(SEM)下的观察结果相符,如图5所示。倾斜角度较小的裂纹,其扩展路径易转向表面发展,进而形成疲劳剥落;而倾斜角度较大的裂纹,倾向于向材料内部扩展而不是转向表面。

(a)裂纹倾斜角度15°

(b)裂纹倾斜角度30°

(c)裂纹倾斜角度45°

(d)裂纹倾斜角度60°图4 不同的初始裂纹倾斜角度下裂纹扩展路径

(2)初始裂纹所处深度对裂纹扩展路径的影响。疲劳裂纹萌生位置一般在次表面Hertz应力场范围内,微裂纹深度超过一定值后对疲劳裂纹萌生的作用很小[32],取4种不同初始裂纹深度,保持裂纹长度0.02 mm、倾斜角度30°及其他外部条件不变,图6所示为裂纹扩展路径计算结果。从图6中可以看出,4种不同初始裂纹深度下裂纹形状比较相似,但深度的变化导致裂纹延伸到表面的时间和最终剥落区域大小产生差异。随着初始裂纹深度的增大,最终的裂纹路径也越来越往基体材料内部生长;同时深度增加意味着Hertz应力场的影响减小,裂纹扩展速率变慢且难度增加,扩展到表面就需要更长的时间,裂纹远表面端也难以快速转向表面,这样就使得深层裂纹的长度和跨度均变大,导致较大面积的剥落。

(a)小角度裂纹扩展路径

(b)大角度裂纹扩展路径

(a)深度0.05 mm

(b)深度0.10 mm

(c)深度0.15 mm

(d)深度0.20 mm

(3)初始裂纹长度对裂纹扩展路径的影响。金属材料在损伤力学中定义的微元通常是在0.1 mm范围内[33],考察0.01 mm、0.02 mm、0.03 mm和0.04 mm等4种初始裂纹长度下疲劳裂纹扩展行为。保持初始裂纹深度0.05 mm、倾斜角度30°及其余外部条件不变,图7所示为不同初始裂纹长度的扩展路径计算结果,可以看出,4种不同初始裂纹长度下裂纹扩展路径差别较小。随初始裂纹长度的增加,裂纹近表面端的生长路线与表面的夹角逐渐变小,远表面端的扩展路径大致相同,均为先沿着初始裂纹方向往基体材料内部发展,再出现转向表面的趋势。

(a)裂纹长度0.01 mm

(b)裂纹长度0.02 mm

(c)裂纹长度0.03 mm

(d)裂纹长度0.04 mm

3.2 初始裂纹不同特征对疲劳裂纹扩展的作用机理

(1)初始裂纹倾斜角度对裂纹扩展的作用机理。采用围道积分法获得初始裂纹倾斜角度不同时的应力强度因子变化规律,如图8所示,进而分析其对裂纹扩展的影响机理。图8中曲线表示的是裂纹未发生扩展时一个滚动应力循环下应力强度因子的变化趋势,横坐标代表最大接触应力相对裂纹中心(坐标为0)的位置。

(a)张开型(Ⅰ型)

(b)滑开型(Ⅱ型)图8 不同初始裂纹倾斜角度下应力强度因子变化趋势

图8a所示为Ⅰ型开裂模式下的应力强度因子变化趋势,可见Ⅰ型开裂模式时的裂纹尖端应力强度因子均为负值,这表明在受压情况下裂纹不会张开反而会出现闭合效应,此时裂纹不会发生扩展。Ⅰ型模式下的几种不同倾斜角度的裂纹尖端应力强度因子变化趋势相同,其值从接近0逐渐减小至谷值,然后又增大到0附近。这是因为在最大接触应力由远及近逐渐到达裂纹中心的过程中,压应力作用增大,使应力强度因子减小;过了裂纹中心后,接触应力的作用变小,裂纹闭合效应随之减小,应力强度因子值复又增大。随着初始裂纹倾斜角的增大,应力强度因子的谷值与0的差距缩小,因为裂纹角度越小,裂纹面承受的压应力越大,导致应力强度因子谷值增大,裂纹以Ⅰ型开裂模式扩展的阻力也变大。

图8b为Ⅱ型开裂模式时应力强度因子随倾斜角度变化的趋势图,可知,Ⅱ型开裂模式是裂纹发生扩展的主要驱动模式,与前文仿真裂纹扩展路径表现出的特征比较吻合。当最大接触应力接近裂纹中心时,Ⅱ型开裂模式应力强度因子值先是从0增大到峰值,再从峰值减小到谷值,在这一过程中,上方裂纹面承受压应力的切向分量导致裂纹面出现正向滑动,且滑动位移逐渐增大直至峰值;然后接触应力接近裂纹中心时下方裂纹面开始滑动,两个裂纹面的相对滑动方向出现了一次改变,应力强度因子也随之减小;而接触应力远离初始裂纹中心后,作用于裂纹面的力逐渐减小,裂纹面之间的滑动方向再一次改变,又从最小值增大到0。滚动载荷作用下两次裂纹面相对滑开方向的改变,将会促进裂纹的疲劳损伤。随着初始裂纹角度的增大,Ⅱ型开裂模式的应力强度因子峰值在前半段减小,后半段又增加,即前半段倾斜角度小的初始裂纹易发生裂纹面滑移,而后半段反之。另一方面,随着初始裂纹倾斜角度的增大,峰值点和谷值点向左移动,这是由赫兹接触的位置决定的,倾斜角度不同时,裂纹顶端在接触正下方的位置不同。

(2)初始裂纹所处深度对裂纹扩展作用机理。同样考察处于不同深度的起始裂纹两端应力强度因子变化规律。图9a为一个应力循环下Ⅰ型模式应力强度因子随裂纹所处深度变化的趋势图,可以看到,Ⅰ型模式的应力强度因子变化趋势与上一节中比较相似,在载荷移动时,应力强度因子值从接近0逐渐减小,达到最小值后又增大直至趋于0。当原始裂纹所处深度变大时,应力强度因子谷值随之减小。这是因为对深度较深的裂纹来说,表面接触应力导致的应力场的影响随深度逐渐变小,所以应力强度因子值就相应地减小。Ⅰ型模式下裂纹尖端应力强度因子幅值随初始裂纹所处深度的增大会逐渐减小,这说明裂纹深度越浅,受到压应力作用形成的裂纹闭合效应越明显。

图9b为Ⅱ型模式应力强度因子随初始裂纹深度变化的趋势图。当接触应力接近初始裂纹中心位置时,Ⅱ型开裂模式应力强度因子值先是从0增大到最大值,此时裂纹面是正向滑移;再从峰值减小到谷值,裂纹面出现反向滑移,之后接触应力接近裂纹中心时,应力强度因子又从最小值增大到0,近似正弦变化规律。在初始裂纹所处的深度不同时,Ⅱ型开裂模式的应力强度因子变化曲线是不相同的,随深度的增加,峰值和谷值逐渐减小,说明裂纹面的滑动随深度增加而减少,深度增加,裂纹扩展的难度也随之增加。

(a)张开型(Ⅰ型)

(b)滑开型(Ⅱ型)图9 初始裂纹深度不同时应力强度因子变化趋势

(3)初始裂纹长度对裂纹扩展作用机理。起始裂纹的长度不同时两端应力强度因子变化规律如图10所示。图10a为一个应力循环下Ⅰ型模式应力强度因子随裂纹长度变化的趋势图,可以看到,Ⅰ型模式的应力强度因子变化趋势仍旧与前面相同,随载荷的移动,应力强度因子值从接近0逐渐减小,达到最小值后又增大直至趋于0。当原始裂纹的长度增大时,应力强度因子谷值随之减小,初始裂纹面承受压应力时,较长的裂纹意味着发生变形的面积更大,裂纹尖端变形更多,所以应力强度因子减小的速度更快。Ⅰ型模式下裂纹尖端应力强度因子幅值随初始裂纹长度的增大会逐渐增大,这说明裂纹长度越长,受到压应力作用形成的裂纹闭合效应越明显,以Ⅰ型模式进行扩展的阻力越大。

图10b为对应情况下Ⅱ型模式应力强度因子随初始裂纹长度变化的趋势图,可见,当接触应力接近初始裂纹中心位置时,Ⅱ型开裂模式应力强度因子值先是从0增大到最大值,裂纹面正向滑移;再从最大值减小到最小值,裂纹面出现反向滑移,之后接触应力接近裂纹中心时,应力强度因子又从最小值增大到0。当初始裂纹的长度不同时, Ⅱ型开裂模式的应力强度因子变化的幅度也不相同,峰值和谷值均随初始裂纹长度增加而增大,这说明裂纹面出现了反复滑移,滑移的量随着长度的增加而增大,但Ⅱ型开裂模式下的裂纹扩展更加容易。

(a)张开型(Ⅰ型)

(b)滑开型(Ⅱ型)图10 初始裂纹长度不同时应力强度因子变化趋势

对比Ⅰ型和Ⅱ型这两种开裂模式的模拟结果,在忽略摩擦力的情况下,三种初始裂纹参数不同时,张开型开裂模式中应力强度因子值总为负值,表明当初始裂纹位于次表面时,张开型模式对裂纹增长没有贡献,反而会因为裂纹闭合效应对裂纹扩展有阻碍作用,裂纹的生长主要是以滑开型开裂模式生长,由剪切应力所驱动。

4 结论

(1)当初始裂纹处于次表面时,张开型扩展模式对裂纹的扩展没有贡献,裂纹主要是在滑开型模式下生长。

(2)初始裂纹的角度对裂纹路径有一定的影响,角度小时整体裂纹跨度小,更易形成疲劳剥落;Ⅱ型应力强度因子幅值和裂纹生长率随裂纹角度增大而减小,但角度在45°之上时重又增大;改变轴承轧制工艺可以一定程度上改善微裂纹角度。

(3)初始裂纹所处的深度对裂纹扩展路径的影响比较大,裂纹越深扩展到表面所需的时间越长,形成的剥落面积越大;随裂纹深度的增大,Ⅱ型应力强度因子幅值呈递减趋势,扩展难度增大;通过热处理手段使次表面气孔减少能够提高疲劳性能。

(4)初始裂纹的长度对裂纹近表面端扩展到表面的路径有着细微的影响;初始裂纹长度越长,Ⅱ型应力强度因子幅值和裂纹生长率越大,裂纹扩展行为更加容易。