五轴曲面铣削的通用表面纹理形貌建模方法
朱思佩 付国强,2 郑 悦 李正堂 杨吉祥
1.西南交通大学机械工程学院,成都,6100312.浙江大学机械工程学院,杭州,3100583.重庆遨博智能科技研究院有限公司,重庆,4000504.华中科技大学机械科学与工程学院,武汉,430074
0 引言
当下机械制造行业产品的结构日趋复杂,对其精度和性能要求日趋提高[1-3]。在普遍的垂直铣削情况下,复杂表面不易加工[4]。五轴机床最多可以实现五轴联动[5],其高自由度在复杂曲面加工制造方面具有独特优势,被广泛应用于航天、航空、航海、汽车、国防等领域。采用五轴机床[6]可得到较好的加工质量及精度[7]并实现复杂曲面的加工。曲面纹理是反映工件表面质量的重要指标[8],曲面纹理质量及走势对工件精度及性能有着不可忽视的影响[9],对高精密零部件至关重要。如非球面反射镜、 发动机叶轮等,其曲面纹理质量直接影响到工件的物理性能、机械性能以及使用寿命等,如零件结合部的接触状态、摩擦表面的磨损、润滑状态、振动、噪声、密封、涂层质量、抗腐蚀性、导电性、导热性和反射性等。对曲面纹理进行建模仿真可以在加工前对工件表面纹理加工结果进行预测,从而降低废品率,提高工作效率[10]。
目前关于表面形貌建模仿真的研究较多,其中Z-map法[11]为常用表面形貌建模方法之一。该模型表达直观、密度可调、结构简单。范思敏等[12]采用该方法对3D环绕法和放射加工法加工的凸球面表面形貌进行了仿真建模。YANG等[13]基于该方法提出了变螺距立铣刀加工曲面表面生成模型。XU等[14]基于该方法提出了一种考虑进给速度变化的球头铣刀加工表面形貌模型。ZHANG等[15]基于该方法建立了AISI H13钢球头铣削表面形貌模拟模型,在考虑材料去除率的前提下优化表面粗糙度。GAO等[16]根据刀面磨损量对切削刃方程进行修正并结合Z-map法建立了铣削表面形貌仿真模型。传统Z-map法求解非线性方程组计算复杂,仿真效率较低,离散化较繁琐。张海[17]改进了Z-map算法并进行仿真建模,无需求解繁琐的非线性方程组。除此之外,还有较多其他建模仿真方法。LAYEGH等[18]基于牛顿迭代法提出了一种预测五轴球头铣削加工表面形貌和粗糙度的解析模型。XU等[19]基于切削刃掠面和N-buffer模型建立了球头铣刀加工表面形貌预测模型。LAVERNHE等[20]基于N-buffer模型建立了能够与进给量预测模型相耦合的加工表面形貌仿真模型。常树禹[21]利用Biharaionic样条曲面插值技术获取刀具切削刃加工扫掠包络面,通过布尔运算更新数值得到了球头铣削加工表面形貌。
表面形貌仿真建模的研究已经较成熟,但大多仅针对特定刀具。JI等[22]考虑刀具与工件多重交互作用建立了五轴球头铣削刀具动力学模型。LOTFI等[23]分析刀具与工件的接触区域,建立了多轴球端铣削加工表面形貌的仿真模型。PRAT等[24]为确定有效切削条件、铣削方式和铣刀定位点建立了五轴球头铣削表面形貌几何模型。DONG等[25]提出了球头铣削在摆线铣削模式下微表面形貌建模方法。CHEN等[26]考虑加工非线性动力学影响建立了平底铣刀微铣削三维曲面仿真模型。ZHANG等[27]提出了考虑刀具系统多阶模态特性和刀具跳动影响的平底铣刀建模仿真方法。ZHOU等[28]为探讨各切削参数对表面粗糙度的影响,建立了环形铣刀铣削表面形貌仿真模型。三种常用铣刀之间几何参数具有一定联系。在此基础上,可进一步对表面形貌仿真建模方法的通用性进行研究。另外,现有表面形貌建模仿真研究多聚焦于优化切削深度、进给量、切削力等工艺条件或者加工条件,并致力于探索刀具磨损、刀具变形等因素对表面形貌的影响,刀具姿态角对表面纹理影响的相关研究还不够完善。XU等[14]建立了一种球头铣刀铣削表面形貌模型,充分考虑了进给速度的影响。ZHANG等[29]针对微铣削建立了一种考虑刀具跳动和动态挠度的曲面形貌生成模型,以探究主轴转速、切削深度等切削参数对表面形貌的影响。ZHANG等[30]考虑刀具磨损提出了表面形貌在线仿真方法。HUANG等[31]分析了刀具跳动和主轴转速调节对高进给速度下织构轮廓的影响。
五轴铣削加工中,刀具姿态角对曲面纹理质量及走势有很大影响,因此加工前,选择一个合适的刀具姿态角范围至关重要。刀具姿态角范围的分类是加工前选择合适刀具姿态角范围的重要依据。目前关于刀具姿态角影响表面纹理形貌的研究中,对纹理形貌质量评价和分类的研究较少,故获取刀具姿态角范围分类缺乏依据。
本文为进一步提高五轴铣削加工曲面纹理形貌仿真建模方法的通用性,以及为后续刀具姿态角分类相关研究提供依据,提出一种通用曲面五轴铣削表面纹理形貌仿真建模方法。该仿真建模方法能够预测五轴铣削加工中不同种类刀具铣削不同种类曲面表面纹理形貌,且能够为曲面纹理形貌质量评价提供支持,有利于后续研究获得曲面纹理形貌质量对应的刀具姿态角范围,为加工前刀具姿态角范围的正确选择提供依据。
1 面向曲面铣削的表面纹理切削过程中刀具切点模型
工件坐标系下刀具切削刃点表达式是加工纹理形貌仿真建模的基础和关键。以具通用性的环形铣刀为例,建立适用于通用曲面的刀触点坐标系,通过坐标转换得到工件坐标系下通用刀具切削刃点表达式。基于此,可由球头铣刀几何特征得到球头铣刀切削刃任一点表达式。
1.1 工件曲面刀触点坐标系下刀具姿态角定义
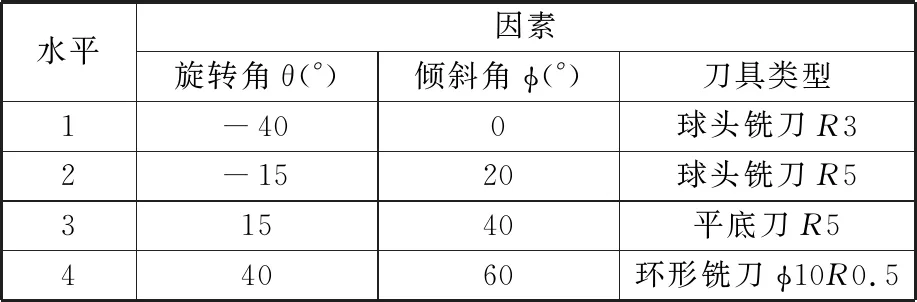
铣削加工中,常用铣刀主要有球头铣刀[30]、平底铣刀及环形铣刀,如图1所示,三者几何参数具有一定联系。球头铣刀和平底铣刀均可通过改变环形铣刀的切削刃半径R1或刀具半径R2得到,故常用铣刀中环形铣刀最具通用性及代表性,本文基于环形铣刀建立曲面工件坐标系下刀具通用切削刃点表达式。
根据五轴铣削加工中刀具绕工件做空间摆动的特点,采用刀具倾斜角φ和旋转角θ来定义刀具位姿。这相较于传统前倾角α和侧倾角β的位姿定义能够更直观形象地反映刀具与工件表面的相对位置及其运动姿态。
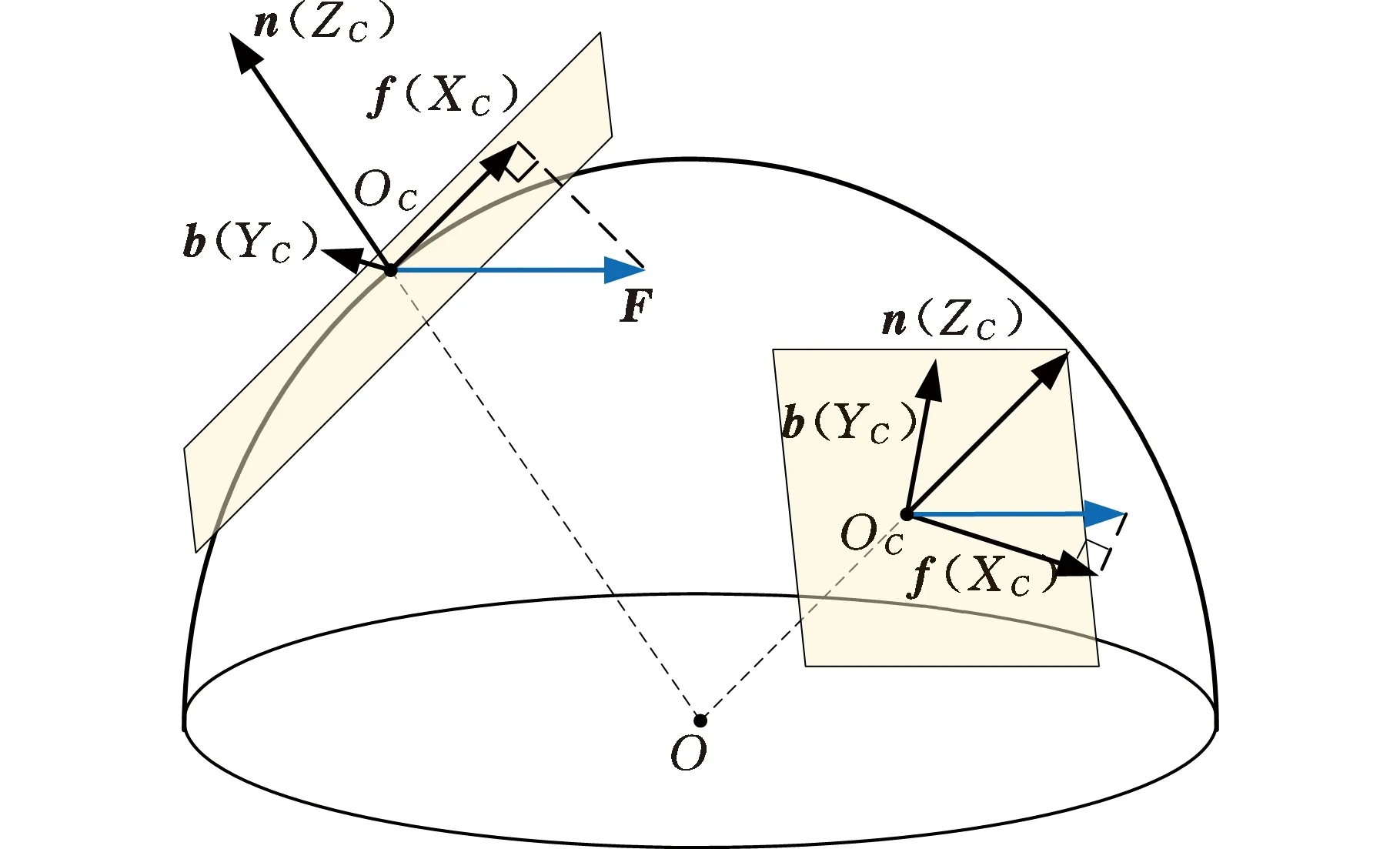
设刀具与工件表面接触点为C,设n=(nx,ny,nz)T为点C处曲面法向量,f=(fx,fy,fz)T为进给方向向量在垂直于向量n平面上的投影,最后根据右手定则求得垂直于向量n及向量f的向量b=(bx,by,bz)T。将三个向量归一化,在点C处建立刀触点坐标系OCXCYCZC,如图2所示,该坐标系适用于不同特征曲面。
刀具倾斜角φ为铣刀轴线与刀触点坐标系ZC轴之间的夹角,旋转角θ为刀具轴线在平面OCXCYC上的投影e与X轴之间的夹角。两者与传统刀具姿态角表示方法,即刀具前倾角α、侧倾角β之间的关系如图3所示,两者之间的数学表达式为
(1)

图3 不同刀具姿态表示之间的关系
环形铣刀切削刃中心相对于刀具中心偏移R1,如图4所示,以切削刃中心为原点建立刀具局部坐标系OLXLYLZL,如图5所示。由上述刀具姿态角定义可得刀具局部坐标系OL相对于刀触点坐标系OC的齐次变换矩阵:
(2)
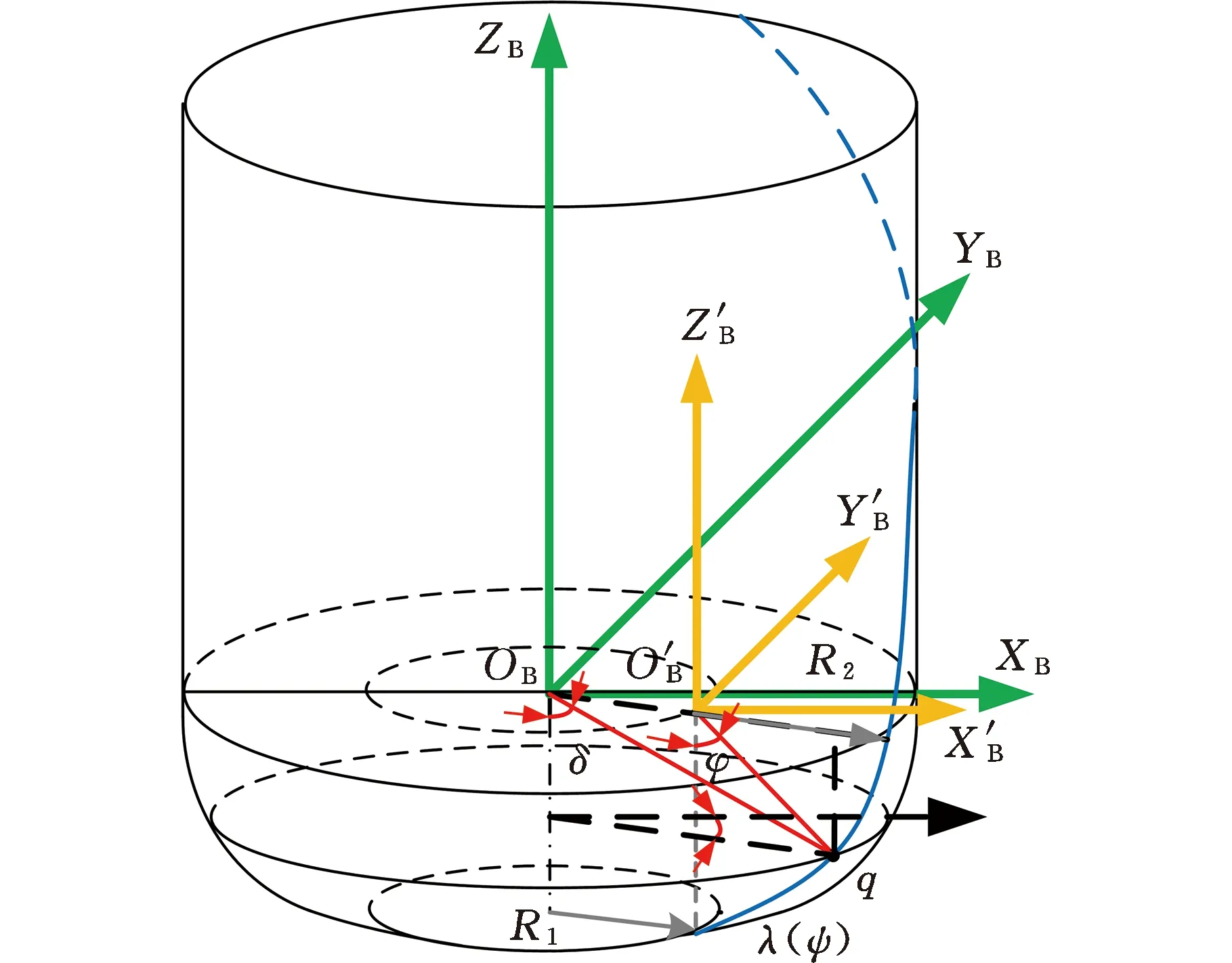
图4 刀具几何形状和刀具第一切削刃坐标系
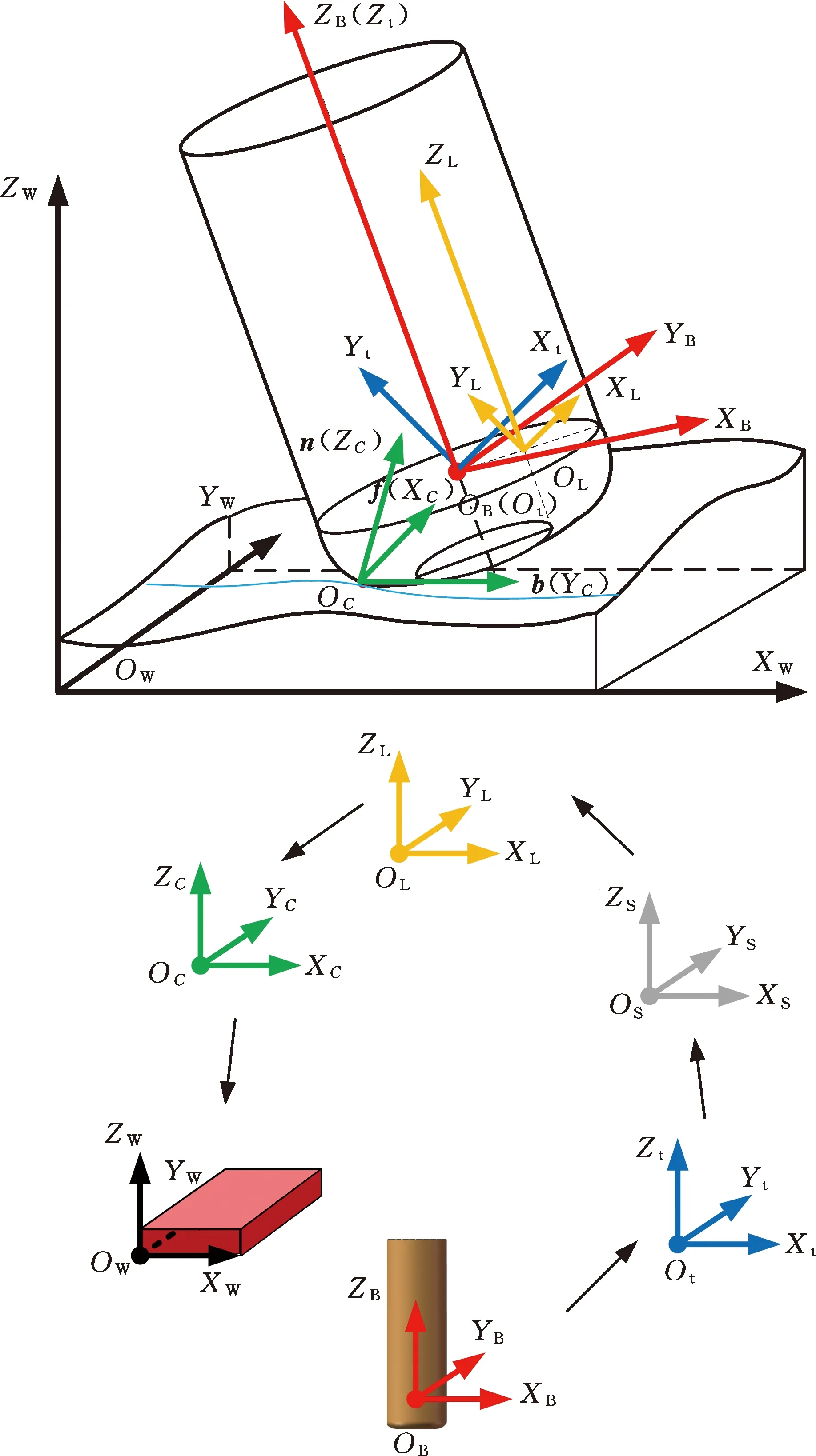
图5 刀具工件坐标转换关系图
根据上述刀触点坐标系定义可得刀触点坐标系OC相对于工件坐标系OW的齐次变换矩阵:
(3)
式中,C为刀触点C在工件原点坐标系下坐标值。
1.2 刀具通用切削刃点表达式
首先建立刀具坐标系OtXtYtZt,其原点位于刀尖点沿刀具轴线上方R2处,OtZt轴和刀具轴线重合。建立第一切削刃坐标系OBXBYBZB,其原点OB与刀具坐标系原点Ot重合,OBXB、OBYB分别与工件的进给方向和行距方向保持平行,如图5所示。
刀具切削刃常选用螺旋刃,故某条刀刃上任一点q在第一切削刃坐标系OB下的表达式为
(4)
式中,l为q与原点OB连线长度;δ为OBq与OBZB夹角;λ为OBXBYB平面上OBq投影与OBXB夹角。
设q点在Z轴上的投影点为qZ,将坐标系沿qZq方向平移R1得新坐标系O′BX′BY′BZ′B。设qO′B在坐标系O′B中与O′BZ′B轴夹角为φ,在O′BX′BY′B平面投影与O′BX′B轴夹角为ψ。根据几何关系,可得转换关系式为
(5)
式中,γ为螺旋角。
将式(5)代入式(4)可得
(6)
环形铣刀上一般有多个刀齿以保证加工效率和加工质量。设铣刀有j个刀齿,第一个刀齿与刀具坐标系OTZT轴的夹角为θ1,则第m个刀齿与OTZT轴正方向的夹角θm满足θm=θ1+2π(m-1)/j,故第一切削刃坐标系OB相对于刀具坐标系Ot的齐次变换矩阵为
(7)
五轴铣削加工中,刀具绕机床主轴以一定角速度ω做旋转运动,建立刀具旋转坐标系OSXSYSZS,其原点OS和刀具坐标系原点Ot重合,OSZS轴和刀具坐标系OtZt轴重合。刀具坐标系Ot相对于刀具旋转坐标系OS的齐次变换矩阵为
(8)
刀具旋转坐标系OS相对于刀具局部坐标系OL的齐次变换矩阵为
(9)
采用单向进给走刀方式进行加工,则刀触点C在任意时刻坐标表达式为
(10)
式中,(x0,y0,z0)为刀具进行第一次进给且t=0时刀具坐标系原点在工件坐标系中的位置坐标;vf为刀具进给速度;i为进给次数;ae为切削行距;zt为t时刻刀触点C在工件坐标系中的位置坐标,与工件表面形状有关。
结合1.1节中坐标变换,刀刃坐标系相对于工件曲面坐标系变换矩阵为
(11)

(12)
式中,X、Y、Z分别为切削刃点在工件坐标系三个坐标轴方向上的表达式。
1.3 球头铣刀切削刃点表达式
根据球头铣刀几何特征,它相对于环形铣刀,R1=0,即Rq=R2。结合式(6)、式(11)、式(12)可得球头铣刀五轴铣削加工过程中刀具切削刃点表达式:
(13)
Xq=x0+Rqnx+vft+Rqcosφ(bxsinθsinφ-
fxcosθsinφ-nxcosφ)-Rqcos(tanγln(cot(φ/2)))sinα·
[bx(cosφcos(ωt+θm)sinθ+cosθsin(ωt+θm))+
fx(-cosθcosφcos(ωt+θm)+sinθsin(ωt+θm))+
nxcos(ωt+θm)sinφ]+Rqsinφsin(tanγln(cot(φ/2)))·
[bx(cosθcos(ωt+θm)-cosφsinθsin(ωt+θm))+
fx(cosωtcosθmsinθ+cosθcosφcosθmsinωt+
cosθcosφcosωtsinθm-sinθsinωtsinθm)-
nxsinφsin(ωt+θm)]
(14)
Yq=y0+(-1+i)ae+Rqny+Rqcosφ·
(bysinθsinφ-fycosθsinφ-nycosφ)-
Rqcos(tanγln(cot(φ/2)))sinφ[by(cosφcos(ωt+
θm)sinθ+cosθsin(ωt+θm))+fy(-cosθcosφ·
cos(ωt+θm)+sinθsin(ωt+θm))+nycos(ωt+
θm)sinφ]+Rqsinφsin(tanγln(cot(φ/2)))·
[by(cosθcos(ωt+θm)-cosφsinθsin(ωt+θm))+
fy(cosωtcosθmsinθ+cosθ·
cosφcosθmsinωt+cosθcosφcosωtsinθm-sinθ·
sinωtsinθm)-nysinφsin(ωt+θm)]
(15)
Zq=z0+Rqnz+Rqcosφ(bzsinθsinφ-
fzcosθsinφ-nzcosφ)-Rqcos(tanγln(cot(φ/2)))sinφ·
[bz(cosφcos(ωt+θm)sinθ+cosθsin(ωt+θm))+
fz(-cosθcosφcos(ωt+θm)+sinθsin(ωt+θm))+
nzcos(ωt+θm)sinφ]+Rqsinφsin(tanγ·
ln(cot(φ/2)))[bz(cosθcos(ωt+θm)-
cosφsinθsin(ωt+θm))+fz(cosωtcosθmsinθ+
cosθcosφcosθmsinωt+cosθcosφcosωtsinθm-
sinθsinωtsinθm)-nzsinφsin(ωt+θm)]
(16)
式中,Xq、Yq、Zq分别为球头铣刀切削刃点在工件坐标系三个坐标轴方向上的表达式。
2 表面纹理形貌仿真
2.1 工件与切削刃离散及单位切削时间确定
将工件离散为M×N个网格微元,取微元长宽相等,即dx=dy。以两点位置角差Δθ将切削刃离散为一定数量切削刃点,相邻两刀刃离散点组成一个刀刃微元。Δθ满足如下关系:刀刃微元lΔ在XY平面上的最大投影长度小于或等于网格微元的长宽,即lΔ≤min(dx,dy)。
为得到理想仿真结果,切削时间也需进行单位离散化。设单位切削时间为Δt,则Δt需满足:Δt内刀刃离散点的扫掠轨迹曲线在XY平面上的投影长度小于等于工件网格微元宽度。单位切削时间Δt内,最大轴向位置角θmax处点扫掠轨迹曲线最长,故以该段曲线为依据。传统Z-map法取工件最小网格宽度作为切削刃离散点最长扫掠长度,由切削刃点轨迹方程得到该切削刃点速度,最后通过求解等式解得Δt。该方法中,单位时间内切削刃扫掠微元仅能扫掠一个工件网格点,仿真效率较低。本文选取仿真开始时刻t1=0,第二个时刻t2=Δt,通过积分运算求得两时刻间(即单位时间步长)切削刃位置角最大点扫掠轨迹曲线长度,根据上述条件列出相应不等式:
(17)
式中,X′、Y′分别为切削刃位置角最大处点在X轴和Y轴方向上的表达式。
最后取Δt最大值作为单位切削时间。该方法中,扫掠四边形内可以有一个以上工件网格点,仿真效率得到有效提高。
2.2 切削刃微元扫掠四边形与工件网格点关系
建立单位切削时间内切削刃微元瞬时扫掠四边形abcd,如图6所示。求得abcd的X、Y轴坐标最大值Xmax、Ymax与最小值Xmin、Ymin,以此得到矩形包围圈ABCD。计算矩形包围圈内工件网格点在X轴网格点位置数最小值ul和最大值ur以及Y轴网格点位置数最小值vu和最大值vd,从而得到落入矩形包围圈内工件网格点最大范围,表达式为
(18)
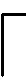
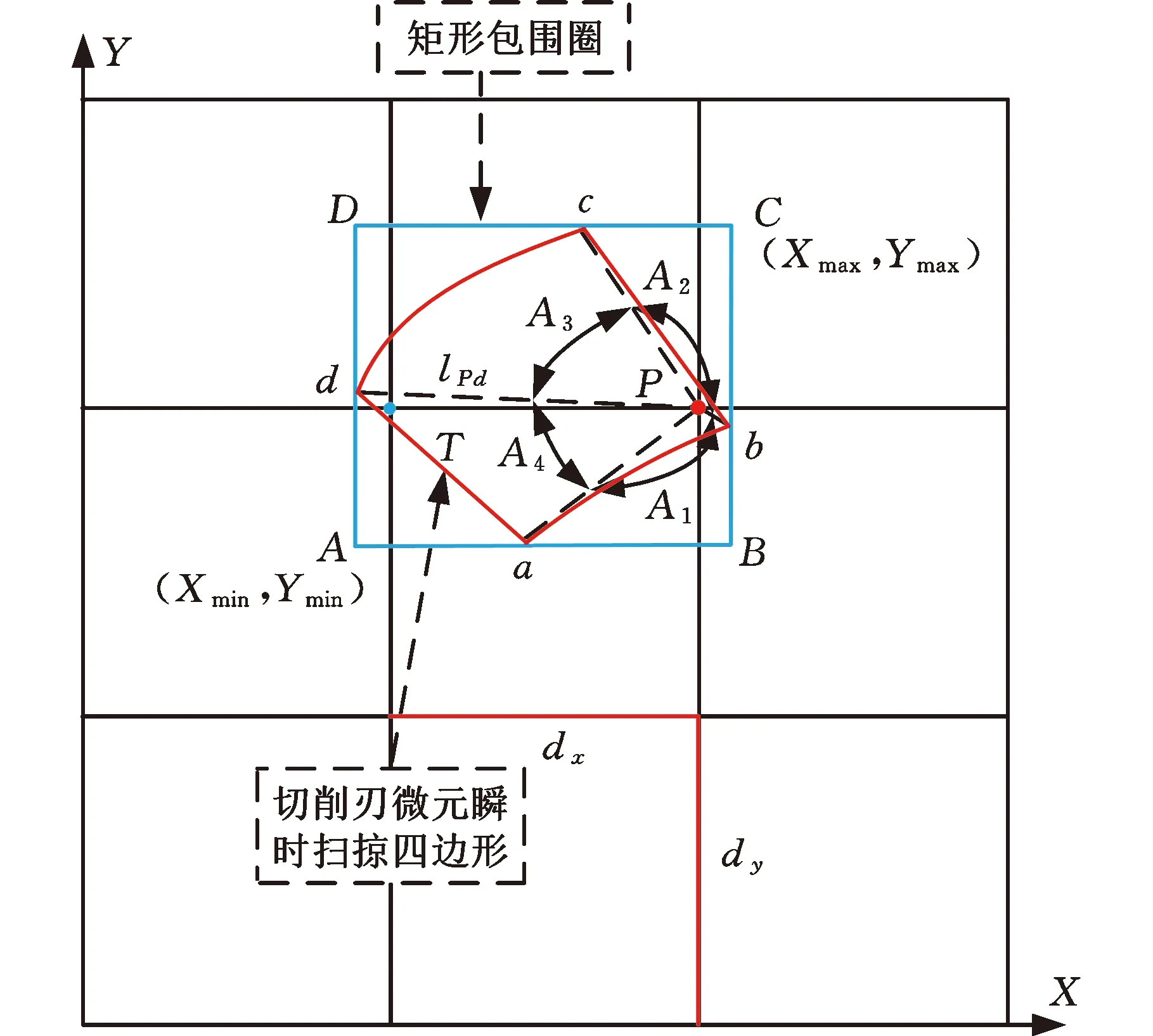
图6 单位切削时间刀刃微元扫掠投影
遍历上述网格点内所有工件网格点得到矩形包围圈ABCD内所有工件网格点。将所有工件网格点位置转换成工件坐标系下坐标(xi,yi),具体计算为
(19)
式中,ui为相应工件网格点在X轴方向网格点位置数;vi为相应工件网格点在Y轴方向网格点位置数。
传统Z-map法通常使用角度累加法判断落入切削刃扫掠四边形的工件网格点,但角度累加法判断过程冗余,效率不高。本文将瞬时扫掠四边形近似为多边形,然后由点与该多边形的几何关系来判断得到落入该四边形内的工件网格点,如图6中点T、P。以P点为例,分别计算瞬时扫掠四边形四个顶点a、b、c、d与P点之间的距离l,以l值最小的点为P点的计算顶点,图6中计算顶点为b。整个表面纹理形貌仿真具体步骤如下。
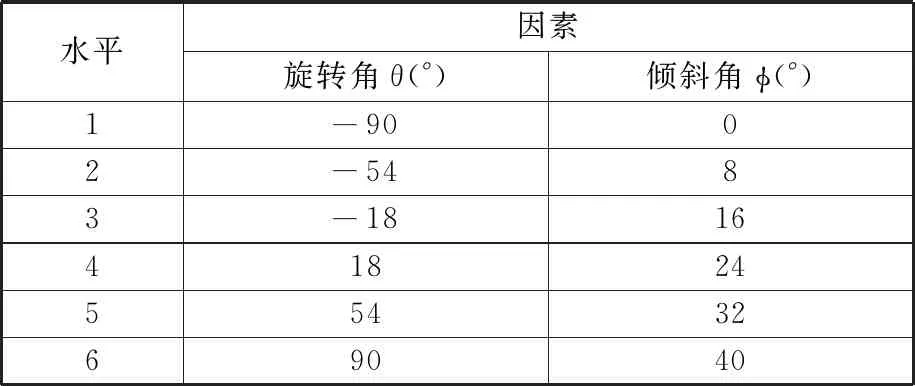
(1)初始化仿真参数:球头铣刀半径Rq、螺旋角γ、切削刃数Zn、工件尺寸M×N×Z、工件初始高度矩阵H(u,v)、主轴转速n、每齿进给量ff、切削深度ap、进给行距ae以及刀具倾斜角φ和旋转角θ。
(2)完成工件切削刃离散化及单位切削时间的确定,如2.1节所述。
(3)判断落入切削刃微元瞬时扫掠四边形的工件网格点。
(4)利用泰勒公式计算瞬时扫掠四边形内网格点对应的切削刃位置角以及扫掠时间,并代入切削刃点表达式得到对应网格点刀具扫掠后高度值并存储在矩阵V(ix,jy)中。
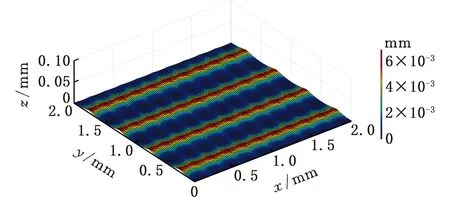
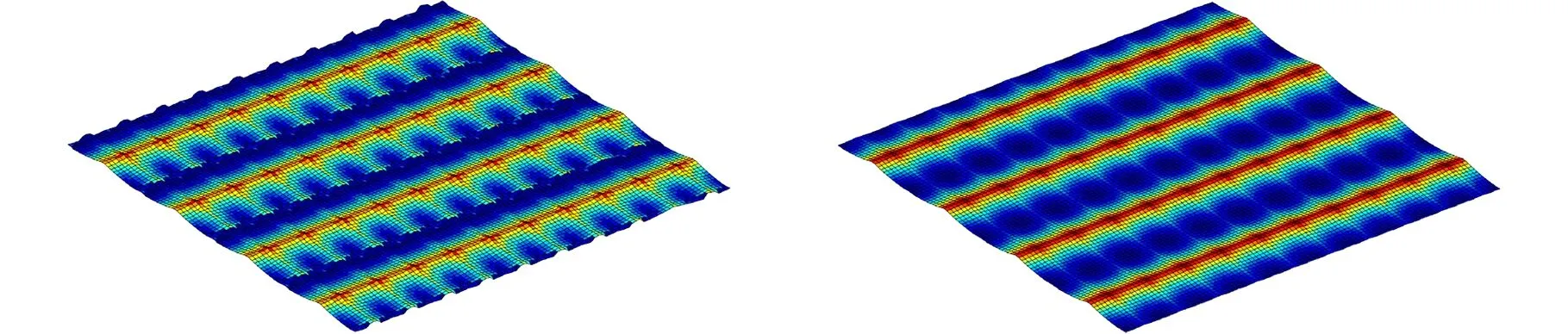
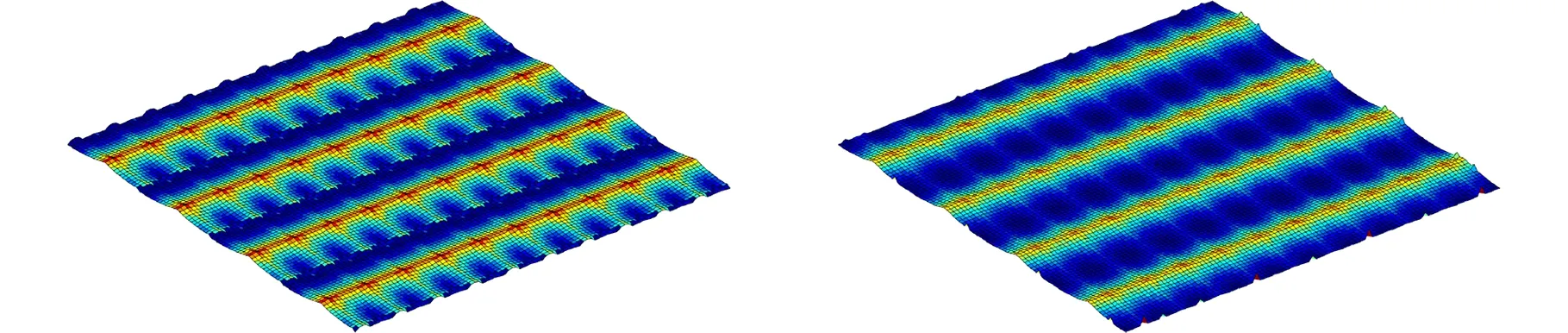
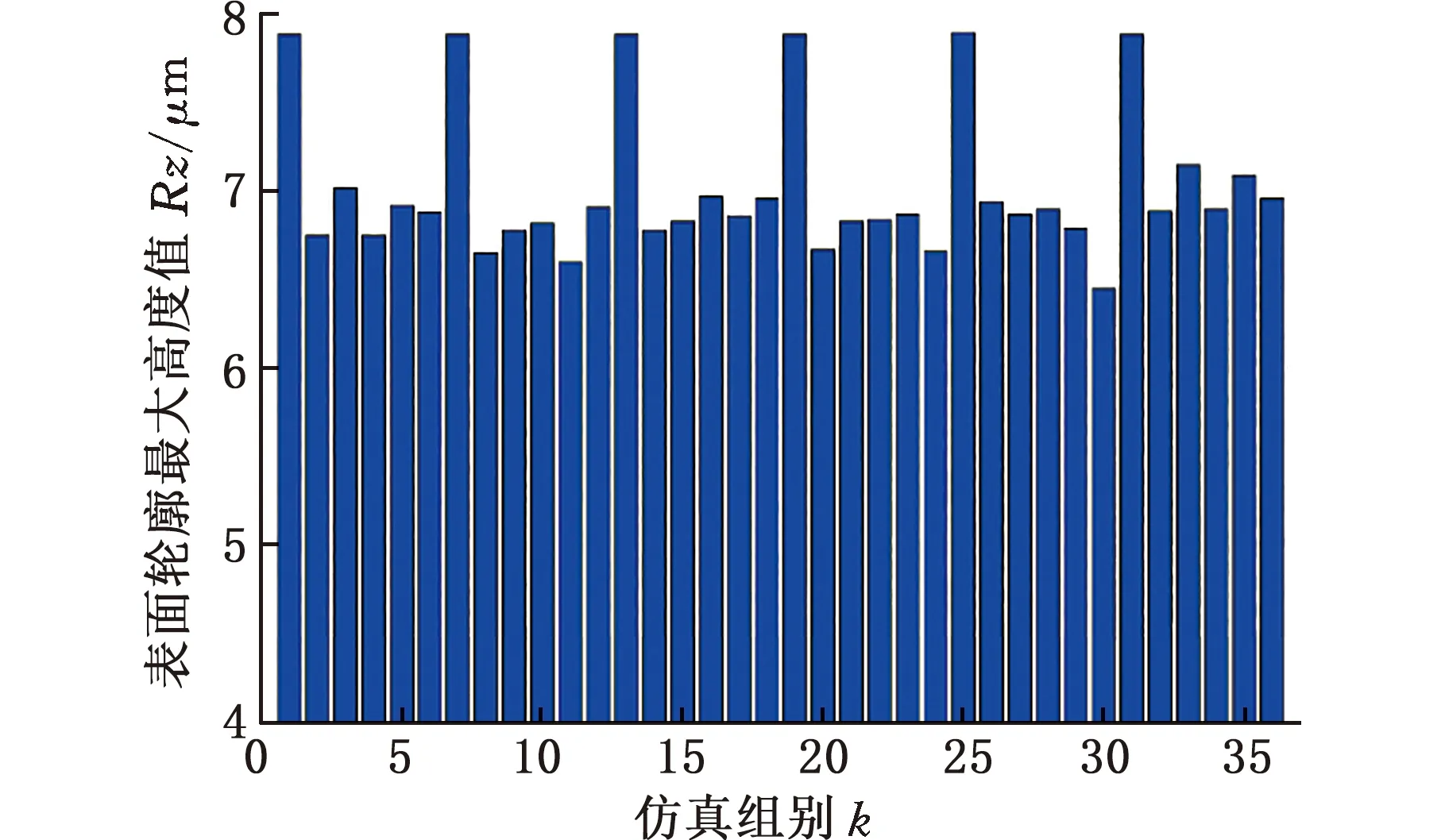
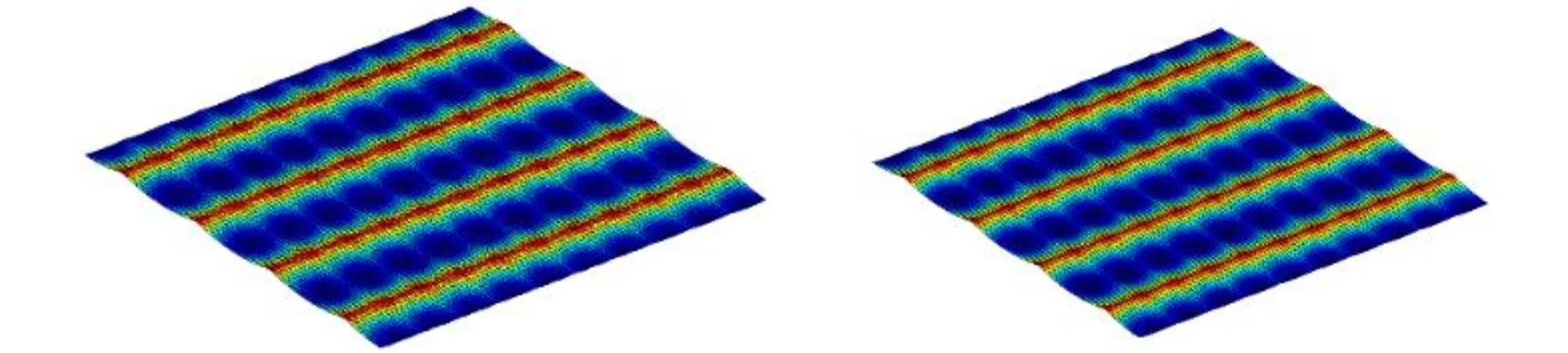
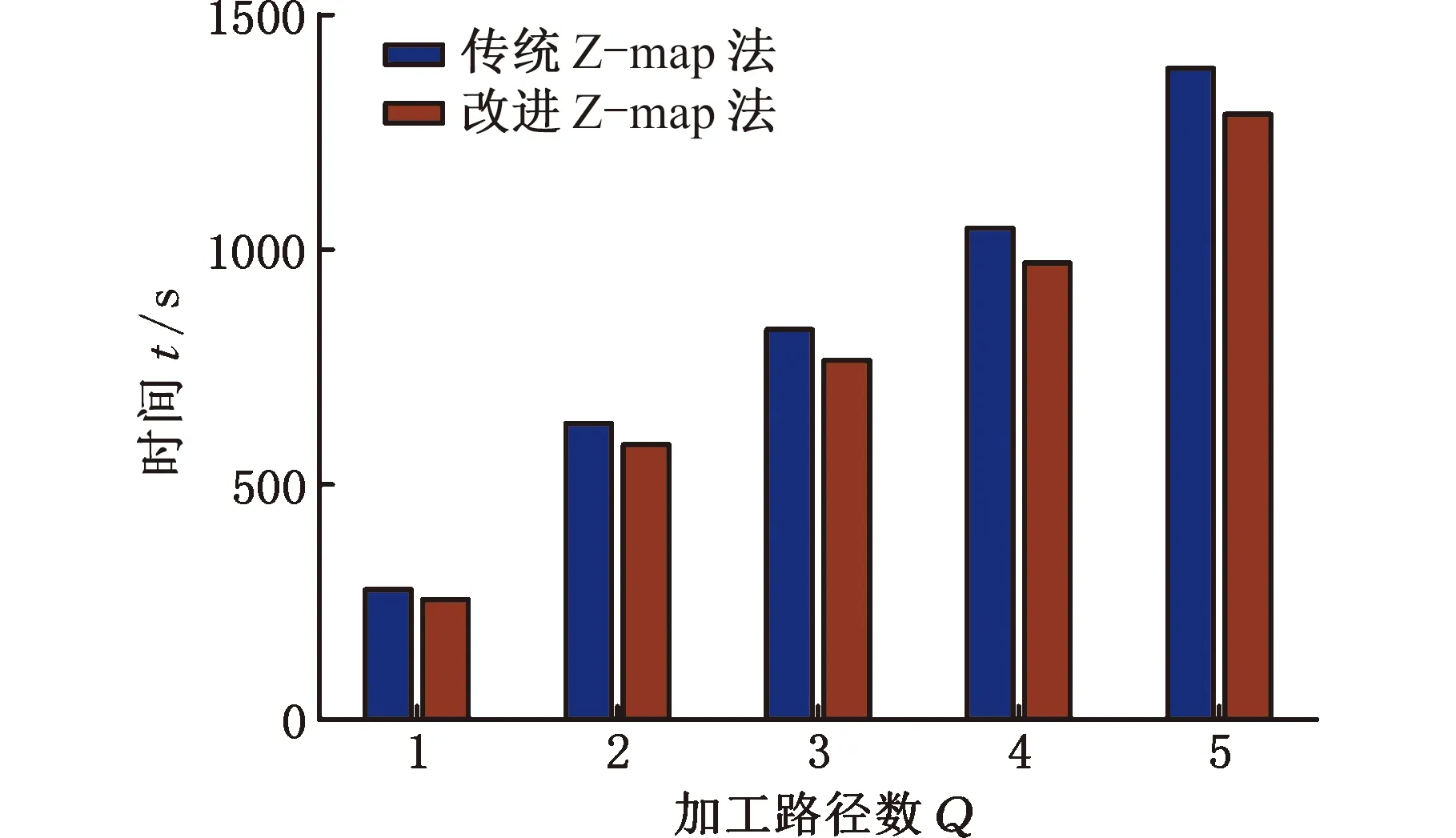
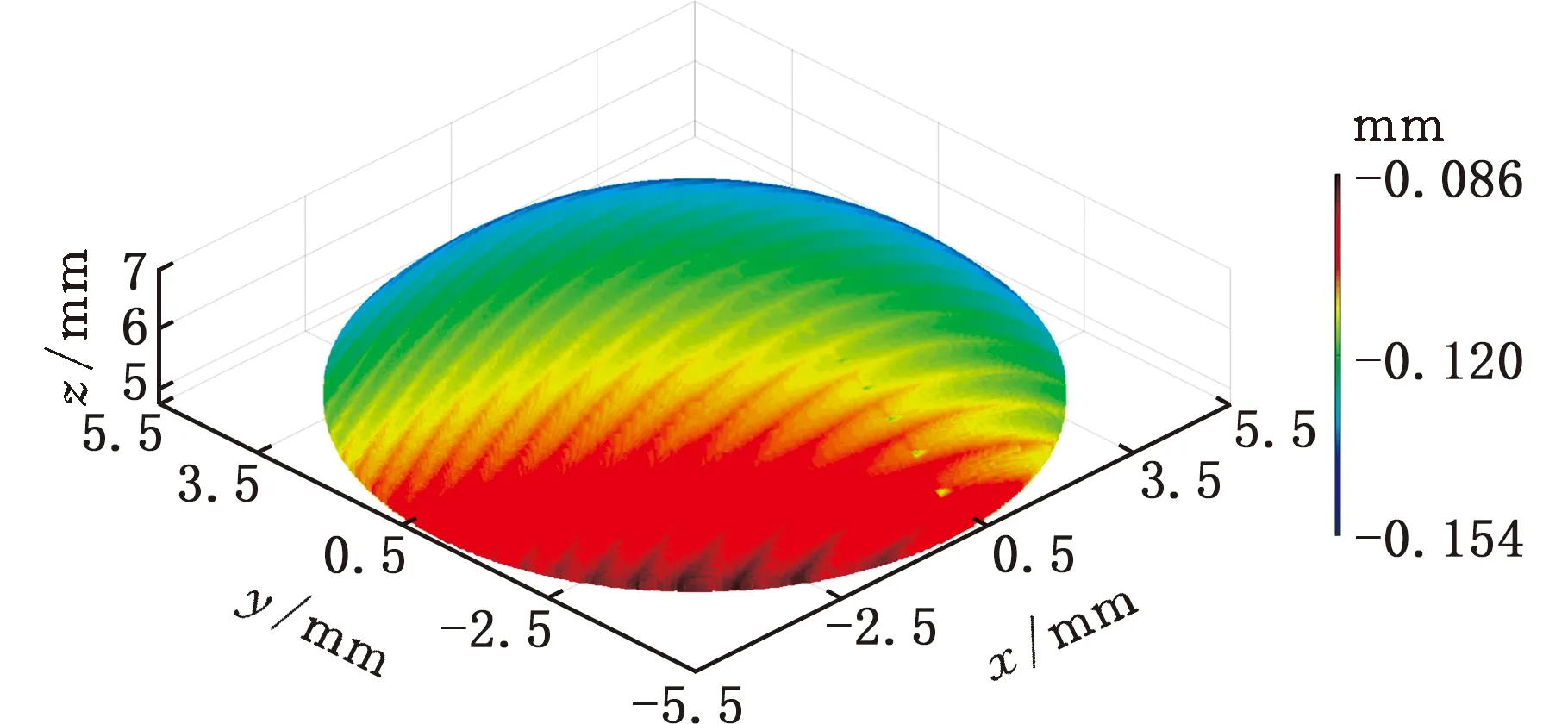
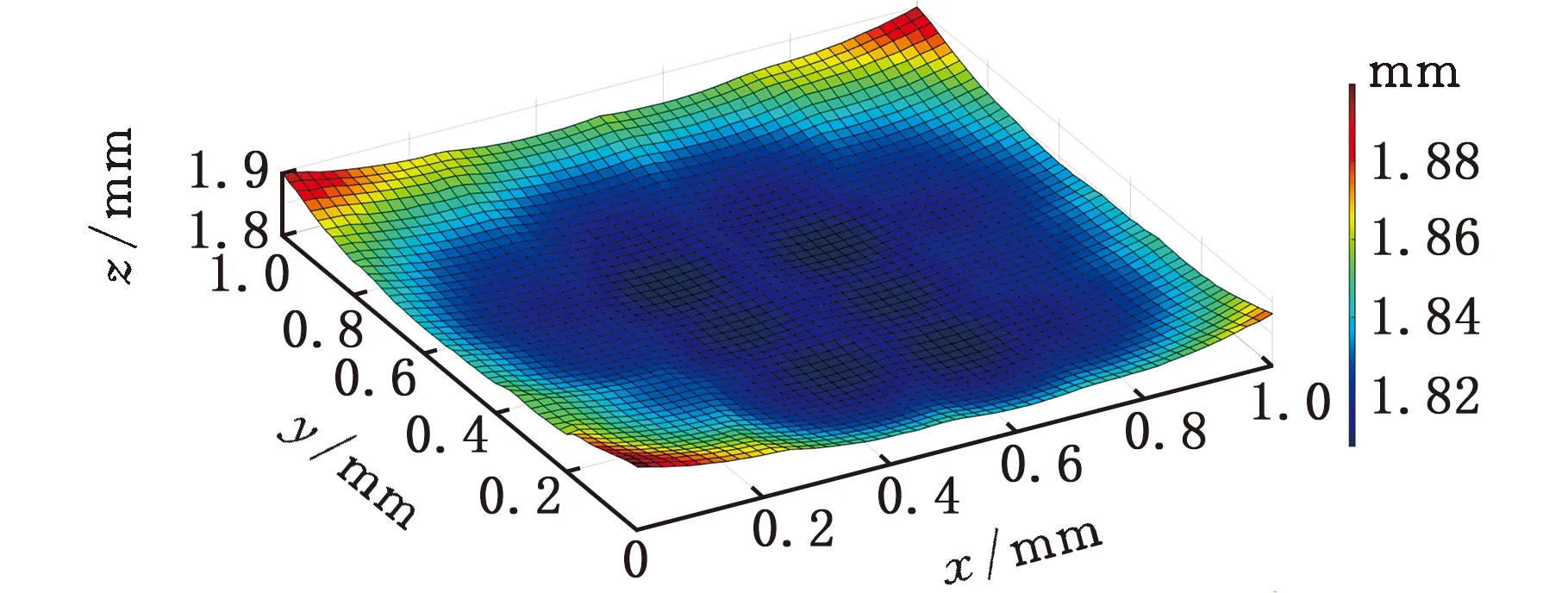
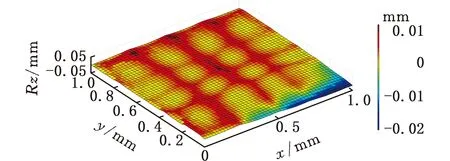
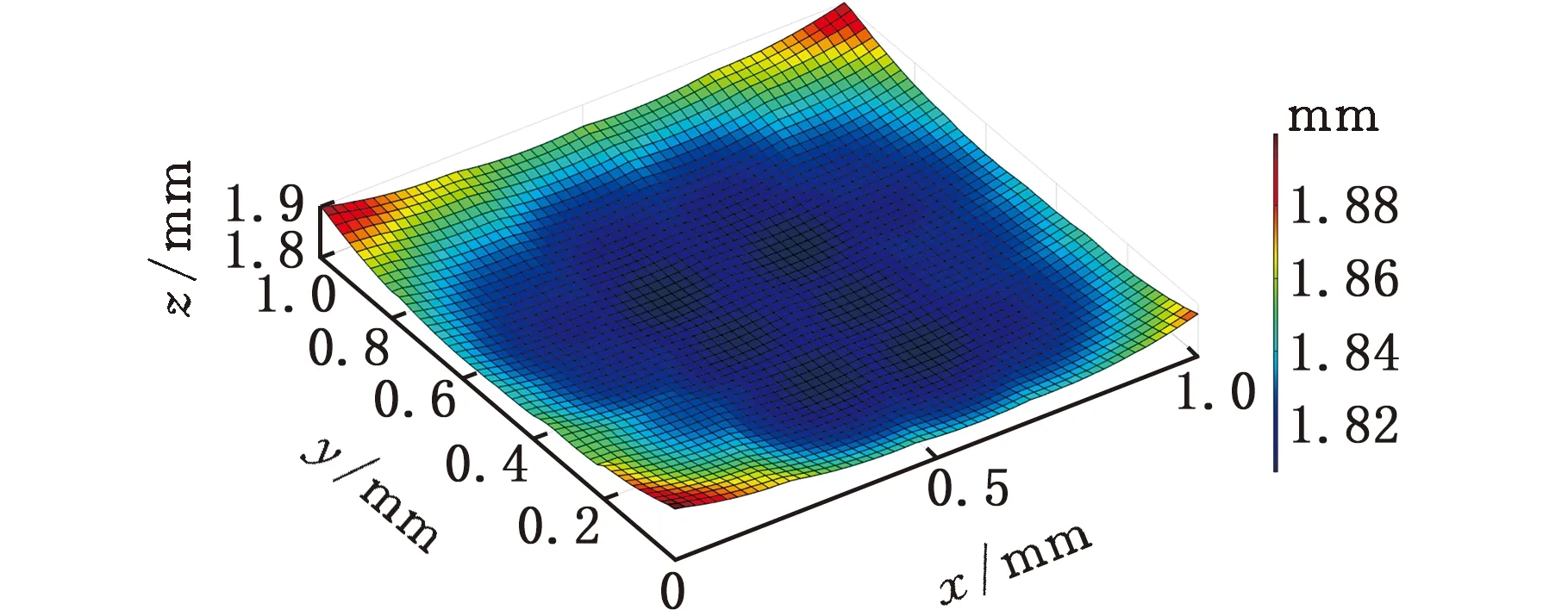
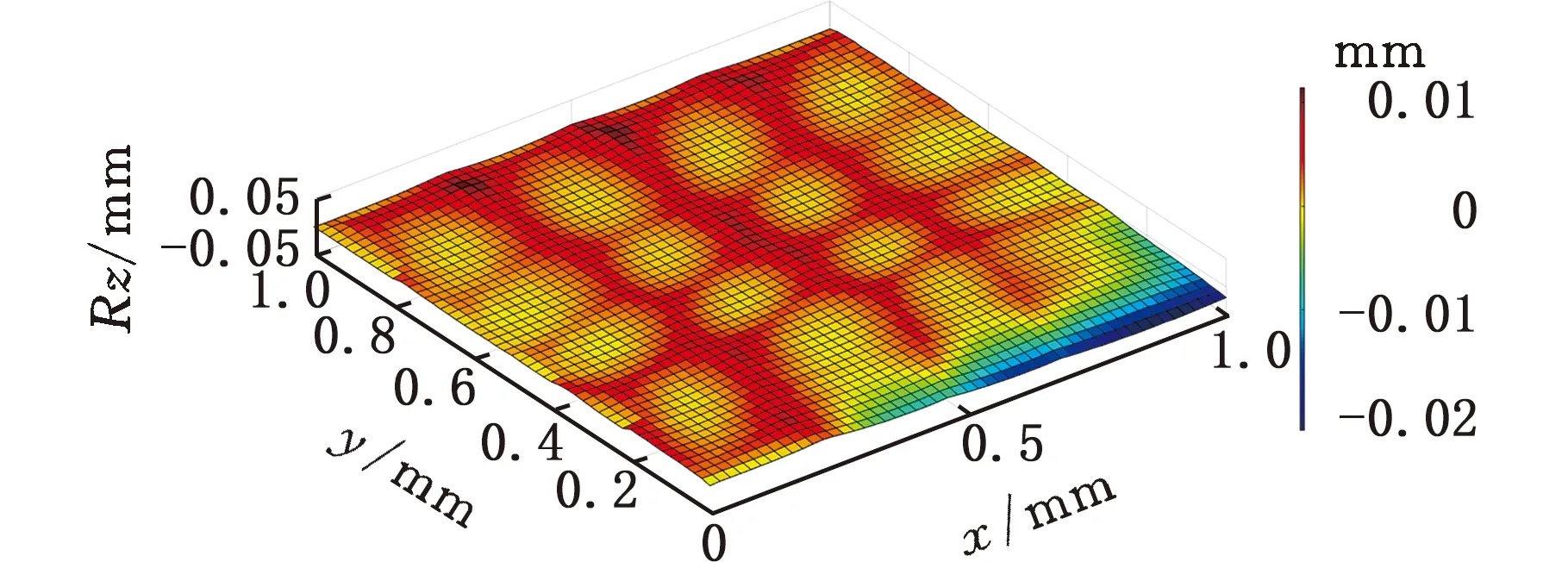
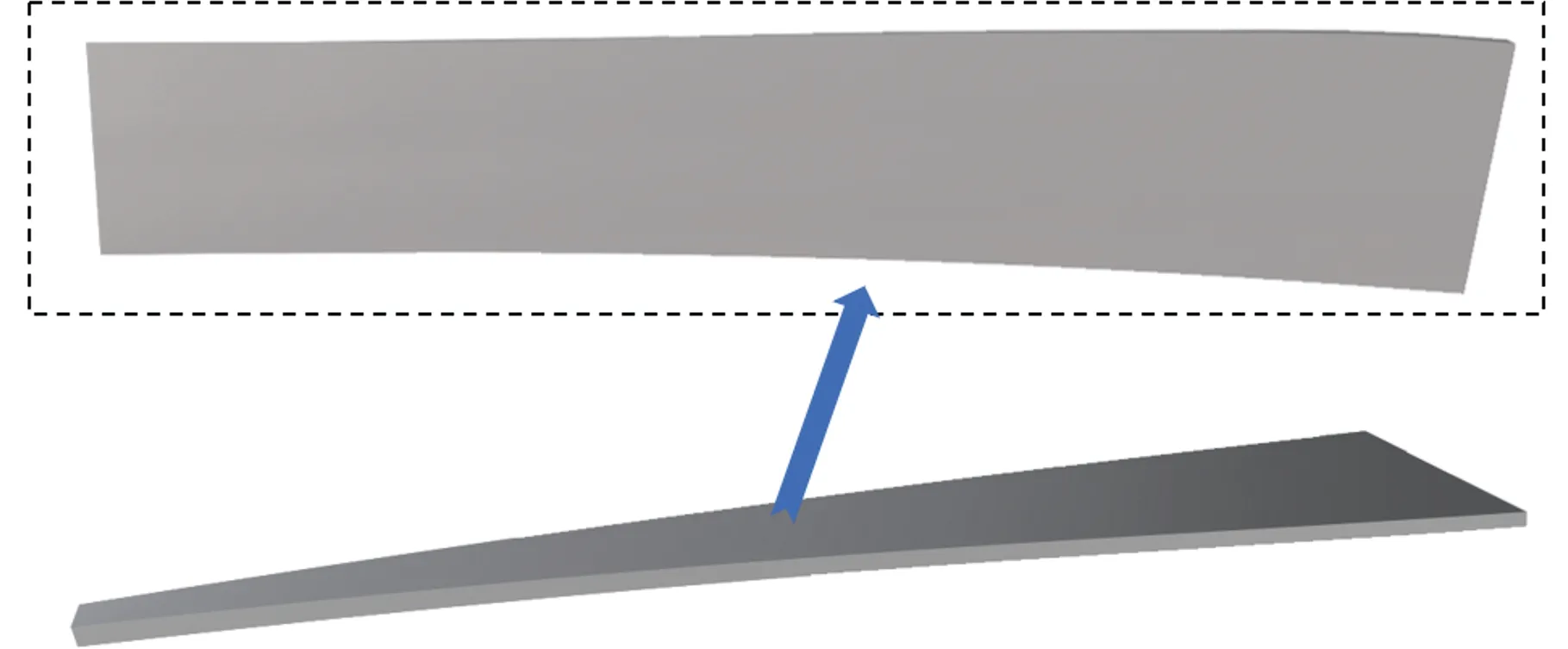
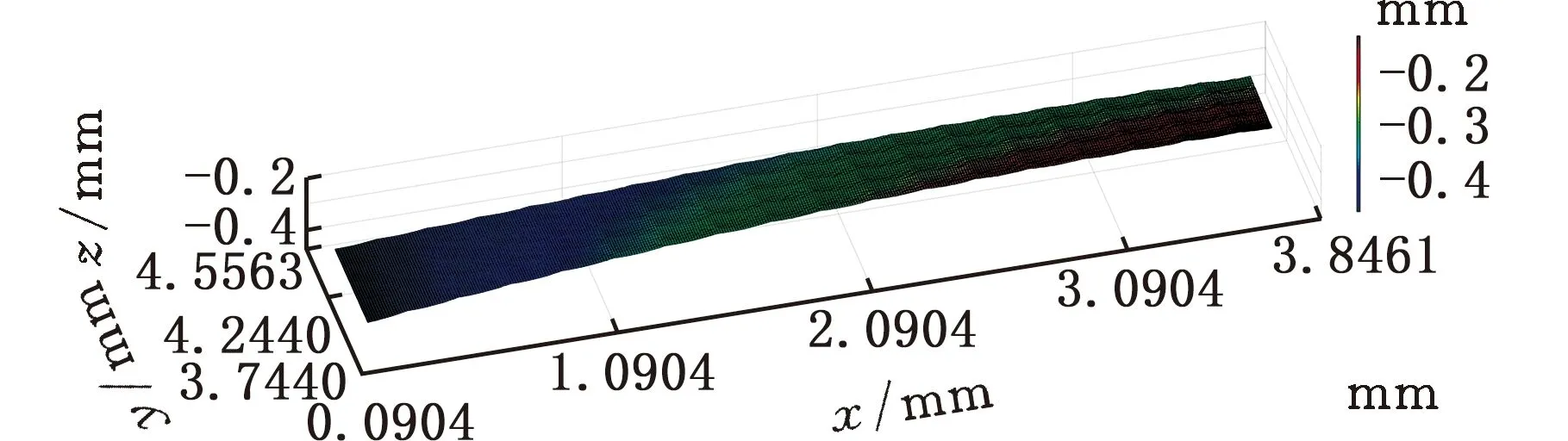
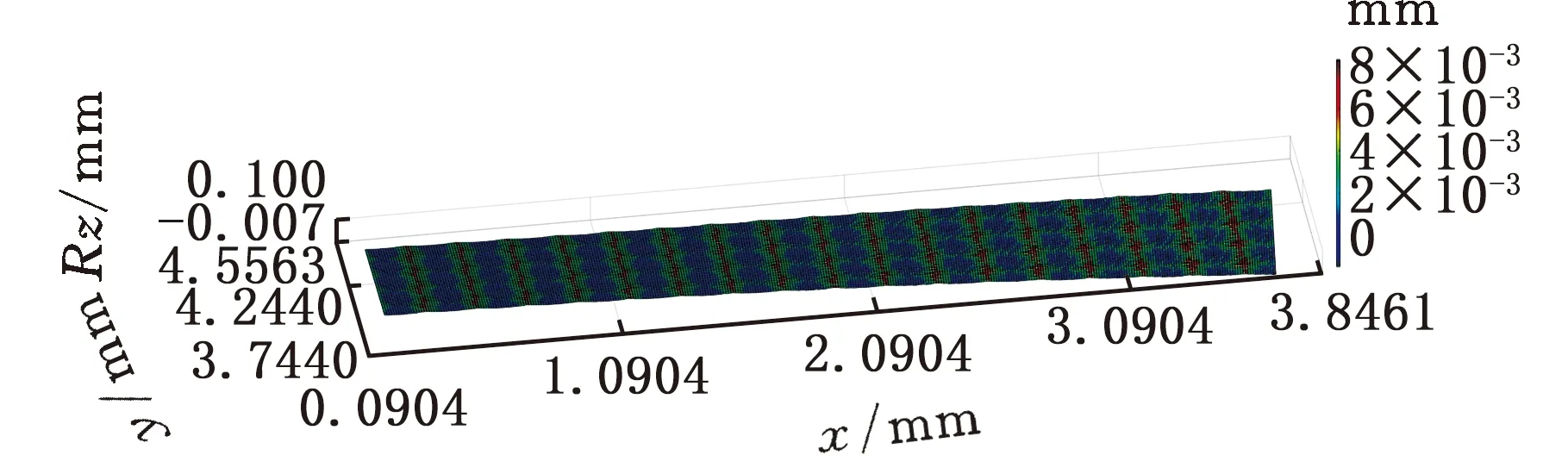
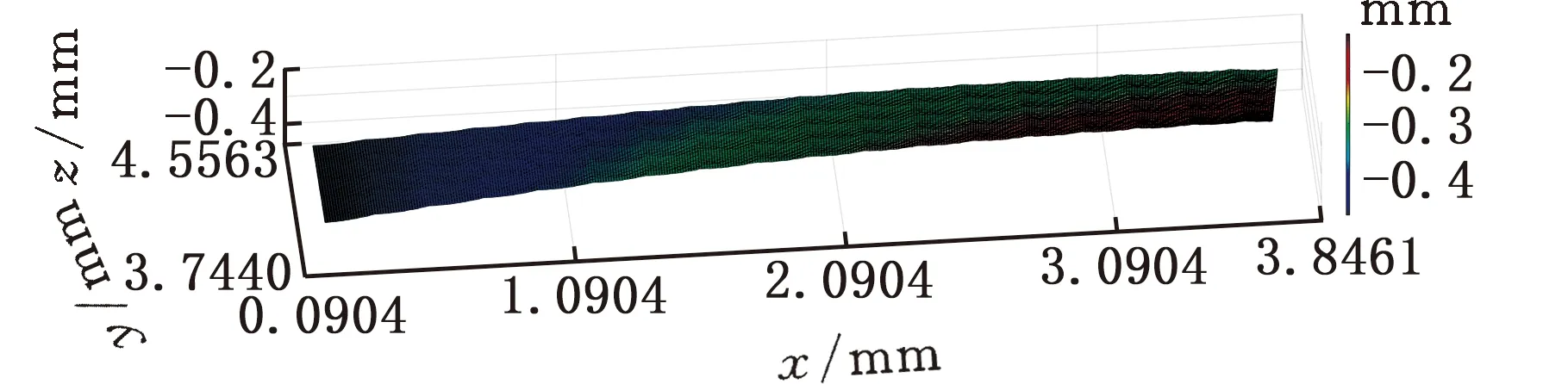
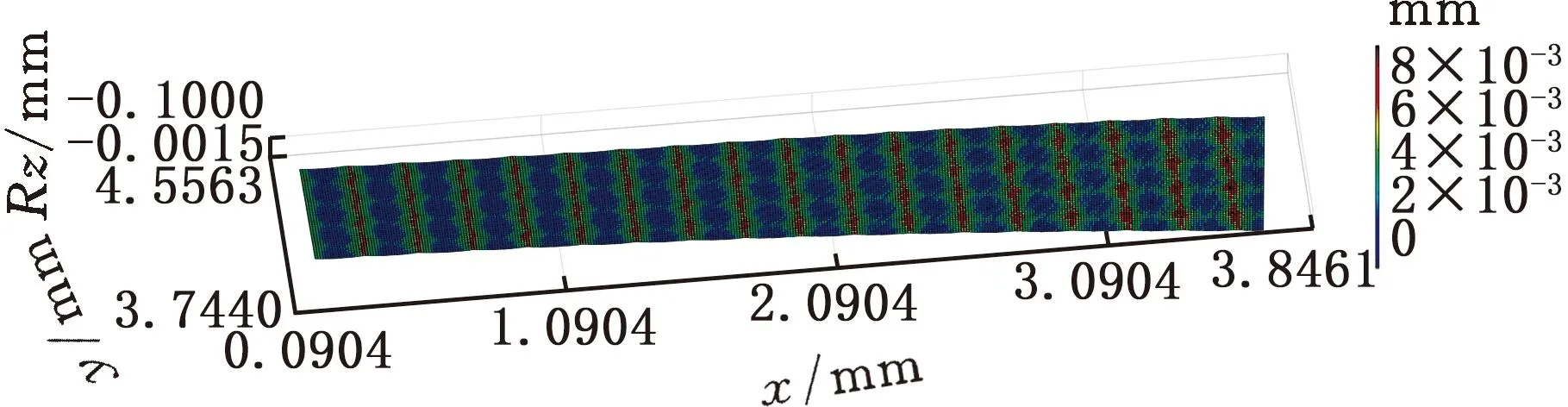
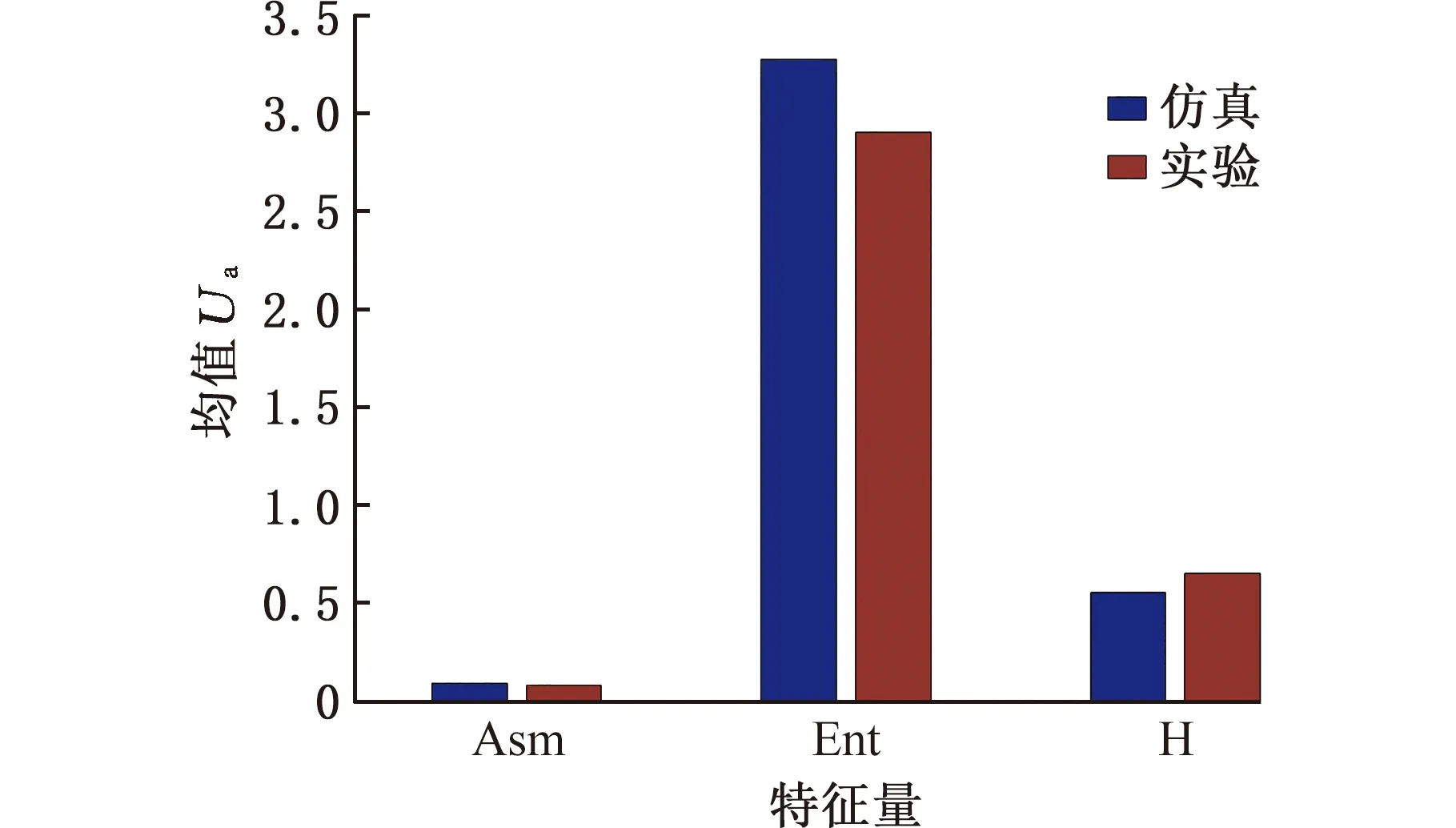
(5)若V(ix,jy) (6)对该切削刃上的每个切削刃点重复步骤(3)~步骤(5)。 (7)对单位切削时间内每个切削刃重复步骤(3)~步骤(6)。 (8)对该次进给的切削时间重复步骤(3)~步骤(7)。 由不同工件曲面几何特征可得其相应刀触点坐标系,进而得到刀具切削刃点运动轨迹。首先建立两种不同几何特征常用曲面即平面和球面的表面纹理形貌仿真模型。为体现本文所提仿真方法的通用性,进一步建立不同类型自由曲面的仿真模型。 3.1.1切削刃点轨迹表达式 对平面进行五轴加工仿真时,当刀具姿态角不变时,刀触点坐标系的方向单位向量f、b、n为固定值,即f=(1,0,0)T,b=(0,1,0)T,n=(0,0,1)T。将f、b、n代入球头铣刀运动学方程(式(14)~式(16))可得加工平面时工件坐标系下刀具切削刃点运动轨迹表达式。 3.1.2仿真模型 选取螺旋角γ=30°、半径Rq=5 mm的球头铣刀。设仿真中主轴转速n=6000 r/min,每齿进给量ff=0.2 mm/r,切削深度ap=0.5 mm,切削行距ae=1 mm。设工件仿真范围为2 mm×2 mm,网格微元大小dx×dy=0.02 mm×0.02 mm。以刀具姿态角θ=-40°、φ=20°进行平面表面纹理形貌的仿真,如图7所示。 图 7 θ=-40°、φ=20°时 平面表面仿真纹理形貌 刀具姿态角对工件表面纹理走势及表面质量的影响不容忽视。进一步使用刀具姿态角,即旋转角θ和倾斜角φ为主要因素进行不同刀具姿态角下平面表面纹理形貌仿真。根据常用刀具姿态角范围,按照表1设计二因素六水平试验表,对平面表面纹理形貌进行36组仿真,如图8所示。 表1 平面仿真正交试验方案 (a)θ=-90°、φ=0° (b)θ=-90°、φ=8° (c)θ=54°、φ=0° (d)θ=54°、φ=40°图8 部分刀具姿态角下表面纹理形貌仿真结果 提取该36组仿真纹理形貌表面最大轮廓高度Ry。如图9所示,倾斜角φ=0°时的表面轮廓最大高度Ry明显大于φ≠0°的组别,而倾斜角φ≠0° 组别中表面轮廓最大高度Rz没有明显差异,因此将切削平面时刀具姿态角范围分为倾斜角φ=0° 和倾斜角φ≠0°两类。 图9 不同仿真条件下表面轮廓最大高度值 进一步对倾斜角较大的情况进行仿真分析,选取4个较大倾斜角与旋转角进行仿真。仿真表面纹理形貌如图10所示,纹理形貌与上述倾斜角φ≠0°时相似。 (c)θ=30°、φ=80° (d)θ=90°、φ=50°图10 大倾斜角下仿真结果 3.1.3与传统Z-map法对比 在同一平面及相同切削条件下,分别运用传统Z-map法和本文所提方法对不同加工路径数进行仿真,仿真时间对比如图11所示。各组别仿真结果显示,本文改进Z-map法仿真时间均明显短于传统Z-map仿真时间。加工2 mm×2 mm工件时有5条切削刀路,每条刀路长度为2 mm。相同切削条件下,若加工100 mm×100 mm工件,仿真时间可减短6.8056 h。 图11 不同加工路径数下加工时间对比 3.2.1切削刃点轨迹表达式 进行球面仿真时,一定刀具姿态角下,刀触点坐标系方向向量f、b、n随刀具在不同的球面位置发生变化,如图12所示。根据1.1节中的分析,f、b、n的具体表达式可由如下步骤求得:首先过球心O得到球面上该位置点处法向量n,并得到垂直于n的平面;然后将刀具进给方向向量F投影到该平面即得向量f;最后由右手定则求得同时垂直于向量n、f的向量b。球头铣刀加工球面时刀触点f、b、n表达式如下: 图12 半球面上不同位置刀触点坐标系 将f、b、n代入球头铣刀切削刃点表达式(式(17)~式(19)),可得五轴铣削加工半球面时工件坐标系下刀具切削刃点的运动轨迹表达式。 3.2.2仿真模型 选取球面半径RB=7.25 mm,刀具倾斜角φ=10°,旋转角θ=-15°,进行球面整体表面纹理形貌的仿真并观察其纹理形貌特征及走势,结果如图13所示。 图13 球面整体纹理形貌仿真残留高度 为观察不同位置处表面纹理形貌,进一步使用不同刀具姿态角对球面不同位置处表面纹理形貌进行仿真。当刀具倾斜角φ=0°、旋转角θ=-15°时,球面上某一位置仿真纹理形貌如图14所示。 图14 θ=-15°、φ=0°半球面某一位置仿真结果 (a)位置1,θ=15°、φ=0°(b)位置1,θ=-15°、φ=40° (c)位置2,θ=15°、φ=0° (d)位置2,θ=-15°、φ=40°图15 球面不同位置投影到同一平面的残留高度 将残留高度投影到同一纬度,结果如图15所示。观察各组仿真纹理形貌特征及颜色分布,同一刀具姿态角下球面不同位置处表面纹理形貌特征相似。 3.3.1自由凹曲面 选取刀具姿态角φ=40°、θ=54°,φ=24°、θ=18°对凹曲面进行表面纹理形貌仿真,结果如图16、图17所示。 3.3.2叶片 首先建立叶片三维模型,然后取刀具姿态角φ=40°、θ=54°,φ=24°、θ=18° 对所建立叶片模型表面纹理形貌进行仿真,叶片模型如图18所示,仿真结果如图19、图20所示。 (a)表面纹理形貌 (b)残留高度图16 θ=54°、φ=40°时凹曲面仿真结果 (a)表面纹理形貌 (b)残留高度图17 θ=18°、φ=24°凹曲面仿真结果 图18 叶片模型图 采用数控加工中心VMC850(图21a)进行切削实验。选取主轴转速n=6000 r/min,每齿进给量ff=0.2 mm/r,行距ae=1 mm,切削深度ap=0.5 mm,采用单向进给走刀方式。加工过程如图21b所示。工件加工完毕后(图21c),使用OLAYMPUS SZX16 体式显微镜(图21d)对每个工件的加工表面进行观测。 (a)表面纹理形貌 (b)残留高度图19 θ=54°、φ=40°时叶片面仿真结果 (a)表面纹理形貌 (b)残留高度图20 θ=18°、φ=24°时叶片面仿真结果 (a)VMC850加工中心 (b)加工过程 (c)部分加工后工件(d)测量使用的体式显微镜图21 实验设备及实际加工示意图 基于该仿真建模方法的通用性,选取几种不同类型铣刀进行切削实验。以刀具旋转角、倾斜角和刀具类型作为变量设计三因素四水平实验,表2为正交试验表。 选取球头铣刀R5,当刀具旋转角θ=-40°、倾斜角φ=20° 及旋转角θ=15°、倾斜角φ=60°时,其表面铣削纹理形貌如图22、图23a所示,仿真纹理形貌如图23b和图24所示。 表2 切削实验正交方案 (a)放大10倍纹理形貌 (b)放大20倍纹理形貌 (c)放大40倍纹理形貌 (d)放大60倍纹理形貌图22 球头铣刀R5,θ=-40°、φ=20°切削后表面观测图 (a)实验 (b)仿真图23 球头铣刀R5,θ=15°、φ=60° 实验与仿真表面纹理形貌对比 由图22~图24比较结果可知,实验表面纹理形貌和仿真表面纹理形貌特征相似,表面纹理走势特征基本一致,验证了该仿真方法的正确性。灰度共生矩阵(GLCM)是研究纹理特征的一种成功的图像分析技术,它通过研究图像灰度的空间相关特性来描述图像纹理特征。根据五轴铣削表面纹理形貌特征选择其主要特征量:能量(Asm)、熵(Ent)、逆差矩(H)。分别对仿真及实际切削表面形貌4个方向进行特征量提取并进行均值计算,计算结果如图25所示。仿真模型提取各特征量均值相对于实验误差的平均值为0.1605。 图24 球头铣刀R5,θ=-40°、φ=20°表面仿真纹理形貌 图25 球头铣刀R5,θ=15°、φ=60° 实验与仿真表面纹理形貌灰度共生矩阵特征量均值提取 球头铣刀在不同刀具姿态角下切削工件的表面纹理形貌观测图见图26。刀具倾斜角φ≠0° 时,表面纹理形貌纹理较规则,刀具倾斜角φ=0°时 ,表面纹理形貌无规则纹理,两种姿态角情况下表面纹理形貌差异较大。切削加工实验所得工件表面纹理形貌特征满足仿真所得刀具姿态角分类,可进一步证明该仿真建模方法的有效性。 (a)球头铣刀R3,θ=-40°、φ=0°(b)球头铣刀R5,θ=-15°、φ=0° (c)球头铣刀R3,θ=15°、φ=40° (d)球头铣刀R5,θ=40°、φ=40°图26 球头铣刀不同刀具姿态角切削表面纹理形貌观测图 (1)基于具有通用性的环形铣刀,通过坐标转换建立刀具通用切削刃点表达式,该表达式同时适用于球头铣刀和平底铣刀,其中所建立的刀触点坐标系适用于不同特征曲面。 (2)通过离散工件、切削刃并求得最大单位切削时间,单位切削时间切削刃微元扫掠四边形内可以有一个以上工件网格点。基于几何关系判断得到落入刀刃微元扫掠四边形工件网格点并通过距离得到相应计算顶点,无需传统Z-map法中角度累加法判断时繁复的计算,计算效率得到提高。结合切削刃点表达式实现五轴铣削曲面表面纹理形貌仿真。 (3)建立常用的不同几何特征曲面即平面和球面以及不同类型自由曲面在不同刀具姿态角下表面纹理形貌仿真模型,根据仿真结果将平面仿真形貌分为φ=0°、φ≠0°两类,通过平面仿真时间对比验证所提仿真方法效率得到有效提高。 (4)在数控加工中心VMC850上进行切削实验,θ=-40°、φ=20°及θ=15°、φ=60°组合下平面实际切削工件纹理与仿真纹理形貌基本一致。同时实际切削表面纹理形貌特征与仿真工件表面纹理形貌分类结果一致,验证了该表面纹理形貌仿真模型有效可靠。本文提出的通用表面纹理形貌建模方法对工件加工表面纹理形貌的预测具有参考意义,能够为后续刀具姿态角分类提供有效依据。3 不同曲面表面纹理形貌仿真
3.1 平面
3.2 球面


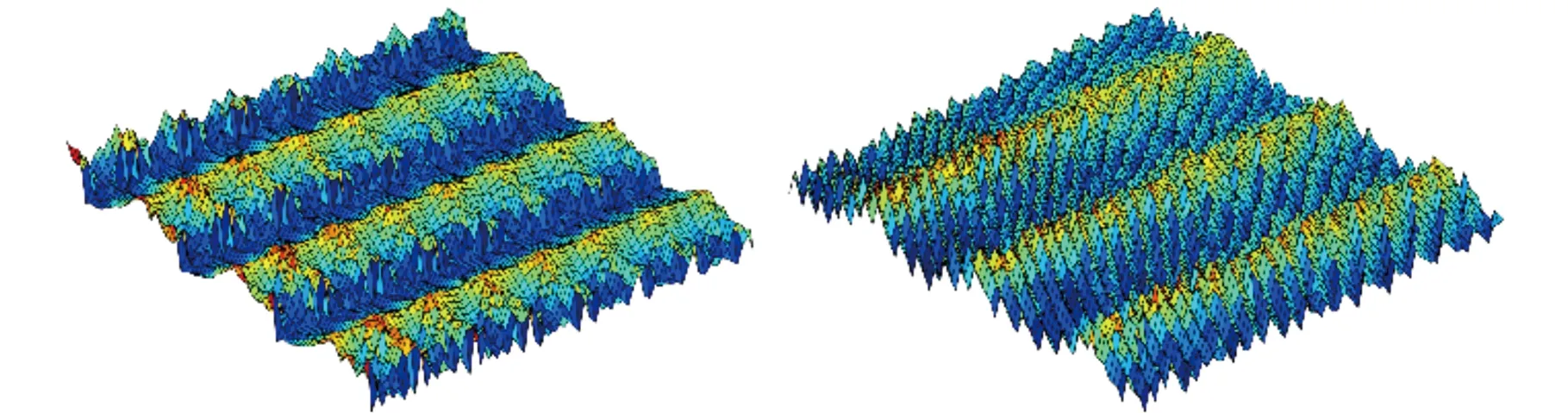
3.3 自由曲面
4 实验验证








5 结论

