我这样教“加减法的关系”
杜永宁

教学“加减法的关系”时发现由学生发现“关系”,不如直接由教师告诉学生结论轻松,但直接讲授结论,学生对二者的关系认识不深刻。课后反复思考怎么引导学生去发现“关系”,理解“关系”,下面主要探讨让学生发现“加减法的关系”策略,具体如下。
一、贴标签,发现关系
课堂导入时,教师板书课题并提出问题:你觉得,这节课会学习到几种关系?学生猜想、归纳为三种关系:加法各部分之间的关系、减法各部分之间的关系、加法与减法间的关系。学习的第一环节是发现前两种关系。
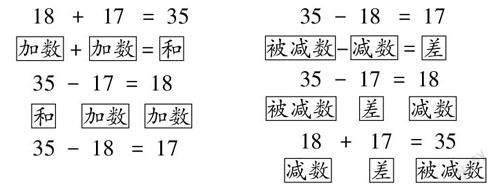
学生根据例题情境(大熊猫繁育基地一共有大熊猫35只。其中成年大熊猫17只,大熊猫宝宝有18只。根据这些信息,可以列出哪些算式?)写出三个算式后,教师按照加法在前和减法在前写板书。接着提示并示范,为了便于描述关系,我们给加法算式里的各个数贴上身份标签(如图),由此得到加法里的第一个关系“加数+加数=和”。然后放手学生去为来自“加法家族”的成员贴上身份标签,为“减法家族”的成员贴上身份标签,加减法各部分的关系被“发现”出来。
为加减法各自的“家族成员”贴标签确认身份,各个成员所处的“位置”不同,表示出来的关系就不同。学生通过“贴”这个操作,经历了“关系”产生的过程,感悟是深刻的。
二、画线段,理解关系
怎么理解加法与减法之间的关系,尤其是理解减法是加法的逆运算?我让学生分别画出例题里的加、减法线段图,最后组合成下面的线段图。借助线段图,学生再次理解加法的意义——把两个数合并成一个数;理解了减法的意义——已知两个数的和与其中一个加数,求另一个加数。在对比两种运算过程中,学生看到加法是求和,而减法是通过和反过去求加数,减法是与加法相反的运算,我们称“减法是加法的逆运算”。虽然这并不是对“逆运算”准确的定义,但也是第一次对“逆运算”做出了形象的刻画。
借助线段图,学生还发现减法里的被减数就相当于加法的和,减數和差相当于加数,加法与减法之间相互改写时就会带着“逆运算”的认知,带着对“关系”的深刻理解来进行,认识更透彻。
三、巧统一,运用关系
求加减法算式中的未知数是加减法关系运用的基本题型,如下题:怎么算出( )里的数?( )-56=120,330-( )=150 ,( )+23=58。但是对于部分初识“关系”的学生,常常弄错“关系”。有没有好方法可以帮助到这些学生呢?教学中,我再次借助上面的线段图把这些关系统一起来。和与被减数都是“总数”,加数、减数和差都是“部分数”,有“总数=部分数+部分数”,所以求总数用加法,已知总数求部分数用减法。学生面对这些题目时,只需要判断哪个是总数,计算方法就随即产生。因为统一的关系简单明了,运用起来就得心应手了。

