钢筋混凝土矮塔斜拉桥地震易损性分析

王国庆, 何沛祥, 郑 攀, 何程瑞伟

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

易损性曲线描述了构件在给定地震动强度条件下,结构地震需求超越结构特定损伤状态的条件概率。大量研究结果表明,结构不确定性参数会对桥梁地震响应和损伤概率造成影响[1-3],但是过多考虑结构参数不确定性将会耗费大量的时间用于有限元模型的非线性时程分析。因此,一些研究者利用代理模型结合实验设计方法或抽样方法建立易损性曲线,文献 [4-7] 研究表明,该种方法能够在保证计算结果精度的情况下,大幅缩短计算所需的时间。本文采用神经网络与均匀设计法相结合的方式建立构件的易损性曲线。在获取构件易损性曲线后,如何获取桥梁系统的易损性曲线成为相关研究的焦点[8-9]。根据串联模型系统的失效概率公式,系统易损性曲线求解关键在于联合失效概率的求解。采用Copula函数建立多维联合分布时,不需限制边缘分布函数的类型,能够灵活方便地构造多维联合分布,因此,该函数具有更广泛的适用性和可扩展性,已经被广泛应用于金融[10]、水利[11]、防灾减灾等领域。文献[12-13]将Copula函数与系统易损性相结合,但主要应用于受力较简单的梁式桥,对于受力更复杂的矮塔斜拉桥的相关研究较少。因此,本文引入Copula函数,研究矮塔斜拉桥的系统易损性曲线,并与一阶界限法[8]比较,验证该方法的可行性与适用性。

1 神经网络方法与Copula函数介绍

1.1 基于神经网络的桥梁地震易损性计算方法

人工神经网络是一种模拟人类神经细胞工作的抽象数学模型,用于模拟一些无法用数学公式严格推导的数学问题。基于人工神经网络与均匀设计法相结合的易损性计算方法如下所述。

1) 选取试验方法、结构不确定性参数和地面运动记录,并将其组成桥梁地震动样本。

2) 采用非线性时程分析法获取构件的地震响应。

3) 将步骤1)和步骤2)中的数据进行配对,组成神经网络训练样本。

4) 调整神经网络参数和结构,直到预测结果精度达到要求。

5) 利用训练好的神经网络对随机抽样的桥梁地震动样本进行预测,并建立易损性曲线。

1.2 基于Copula函数的系统易损性分析理论

Copula函数、联合分布函数和边缘分布函数之间存在着必然逻辑关系,任何联合分布函数均可由Copula函数和边缘分布函数复合而成[14],即

F(x1,x2,…,xn)=

C(F1(x1),F2(x2),…,Fn(xn))

(1)

其中:F(x1,x2,…,xn)为联合分布函数;C(·)为Copula函数;Fi(xi)为边缘分布函数。

桥梁结构系统可以看成由多个构件组合而成的串联系统。串联系统的失效概率Psys计算公式为:

…+(-1)n-1Pijk…

(2)

其中:Pi为系统中第i个构件单独失效的概率;Pij为系统中第i个构件和第j个构件同时失效的概率;n为系统中所有可能失效构件的数目。

对于桥梁系统易损性曲线,可采用Copula函数求解各个构件之间的联合分布函数(概率)。式(2)中引入Copula函数后,系统的失效概率为:

(-1)n-1C(Pi,Pj,Pk,…)

(3)

求得构件失效概率和构件之间的Copula函数后,采用式(3)便可算出系统失效概率,从而得到系统易损性曲线。

2 计算实例

2.1 矮塔斜拉桥概况及有限元模型

某在建钢筋混凝土矮塔斜拉桥跨径为(80+150+80) m,主梁采用三向预应力混凝土截面梁,跨中梁高为5.6 m,支点梁高为4.0 m。主墩为双肢薄壁墩,单肢矩形截面尺寸为15.0 m×1.8 m。过渡墩为双柱矩形墩,截面尺寸为2.0 m×3.0 m。主塔采用塔高为26.5 m的独柱矩形塔,截面尺寸为3.0 m×5.0 m。全桥呈扇形双索面布置96根斜拉索。1/2实例桥梁示意图如图1所示。

图1 1/2实例桥梁示意图

基于OpenSees软件平台对该桥梁进行有限元建模与分析。已有研究表明,主梁在地震作用下不易发生损坏,基本维持在弹性工作范围之内,因此本文采用无非线性行为的弹性梁单元对主梁进行建模。斜拉索采用Truss单元模拟,过渡墩和主墩的力学行为采用基于纤维截面的非线性梁柱(Nonlinear Beam Column)单元模拟。纤维截面主要划分为3部分,其中保护层混凝土和核心混凝土采用Concrete04本构模型,普通钢筋采用Steel02本构模型。

桥梁结构形式为塔墩梁固结体系,边墩支座通过给零长度单元赋予理想双折线弹塑性材料的方式模拟,斜拉索索力的施加通过赋予对应单元初始应变的方式来模拟。构件有限元模拟示意图如图2所示。

图2 构件有限元模拟示意图

2.2 设计变量和均匀设计方法

根据历史震害调查资料,桥墩和支座是易于发生损坏的构件[15],应给予重点关注。因此,本文选取支座、过渡墩和主墩作为研究对象。为考虑结构参数不确定性影响,选取过渡墩核心混凝土峰值应力(fc1,core)、过渡墩核心混凝土峰值应变(εc1,core)、主墩核心混凝土峰值应力(fc2,core)、主墩核心混凝土峰值应变(εc2,core)和普通钢筋弹性模量(Es)5个材料不确定性参数作为随机变量。将5个随机变量划分为15水平,选取U15(155)均匀表进行实验设计,共获得15组桥梁样本。随机变量的对数正态分布参数见表1所列。

表1 5个随机变量对数正态分布参数

2.3 地震动选取及损伤指标划分

同一结构在不同地震波作用下的非线性时程分析结果存在较大差异[16],因此要保证时程分析结果的可靠性,应选取符合桥址场地条件和桥梁设计参数的地震波。现阶段地震波主要来源于人工生成地震波和历史地震波数据库,本文根据文献[17]给出的设计反应谱,从太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center,PEER)数据中匹配天然地震波。综合考虑地震动持时、震中距等因素,最终选取15条天然地震波用于后续计算。地震波反应谱及均值反应谱曲线如图3所示。

图3 15条天然地震波反应谱及均值反应谱曲线

结构在地震作用下会进入弹塑性受力状态,并发生不同程度的破坏,为便于对桥梁在地震作用下的破坏程度进行区分,常根据损伤指标的取值范围将结构划分为轻微破坏、中等破坏、严重破坏和完全破坏4种损伤状态。本文选取支座位移μ作为支座损伤指标,根据设计文件和文献[17]可得单向、双向活动支座最大纵向允许位移为150 mm。支座4种损伤状态的定义见表2所列。

表2 支座损伤状态划分结果

过渡墩和主墩作为压弯构件,需同时承担轴向压力和地震作用下的水平剪切力,根据其受力特点,本文选取使用较为广泛的截面弯曲曲率作为其损伤指标。截面曲率需要通过弯矩-曲率分析获取,本文采用XTRACT软件对过渡墩和主墩墩底截面进行建模和分析。过渡墩截面的弯矩-曲率关系曲线如图4所示。

图4 过渡墩截面弯矩-曲率关系曲线

根据XTRACT软件的截面弯矩-曲率分析结果,可以得到过渡墩和主墩不同损伤状态下的截面曲率φ取值范围。过渡墩和主墩4种损伤状态的划分结果见表3所列。

表3 过渡墩和主墩损伤状态划分结果 单位:10-3/m

2.4 非线性时程分析及神经网络构建

将15条天然地震波分别调幅至0.1g～1.0g(增量0.1g),并与15组桥梁样本进行随机配对,即可获得150组桥梁地震动样本。对150组桥梁地震动样本进行非线性时程分析,得到用于神经网络训练的初始数据。为确保训练的神经网络具有足够的精度,本文基于TensorFlow平台进行多次试算确定网络结构,最终选取神经元数分别为50、25的双隐含层神经网络,并以Relu作为其激活函数。有限元计算值和神经网络预测值的散点图如图5所示。从图5可以看出,数据点接近直线y=x,表明神经网络预测结果具有较高的精度。

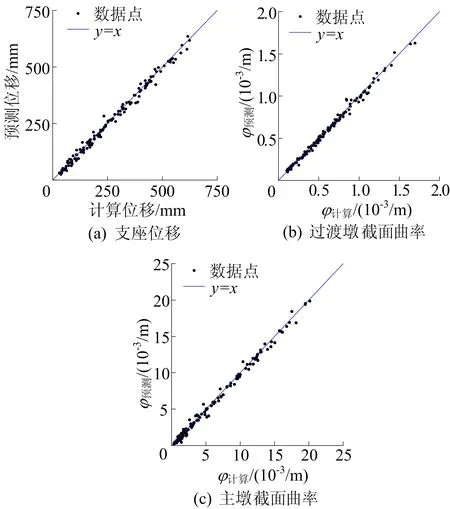
图5 3种构件响应预测值与计算值对比

3 桥梁构件与系统易损性曲线建立

3.1 桥梁构件易损性曲线

概率地震需求模型(probabilistic seismic demand model,PSDM)是在非线性动力时程分析方法的基础上,对结构响应进行回归分析而衍生的一种易损性曲线建立方法。假设构件地震需求D和构件抗震能力C服从对数正态分布,根据易损性的定义可得出构件地震损伤概率Pf计算公式[18]为:

(4)

其中:D|IM为在地震动强度IM下的构件地震需求;βC、βD|IM分别为抗震能力和地震需求标准差。

采用指数函数描述D与IM之间的关系为:

lnD|IM=blnIM+lna

(5)

其中,a、b为线性回归参数。将式(5)代入式 (4)中,Pf可进一步表示为:

(6)

由式(5)、式(6)可知,要求得构件易损性曲线,需要对D|IM与IM进行对数线性回归分析,本文选取常用的地面峰值加速度(peak ground acceleration,PGA)作为IM,对每级PGA下的不确定性参数进行抽样,并用神经网络预测构件的响应值,将预测响应值与IM进行对数拟合,即可得到式(6)所示的关系式。3种构件的D与IM的线性回归方程见表4所列。

表4 3种构件的D与IM线性回归方程

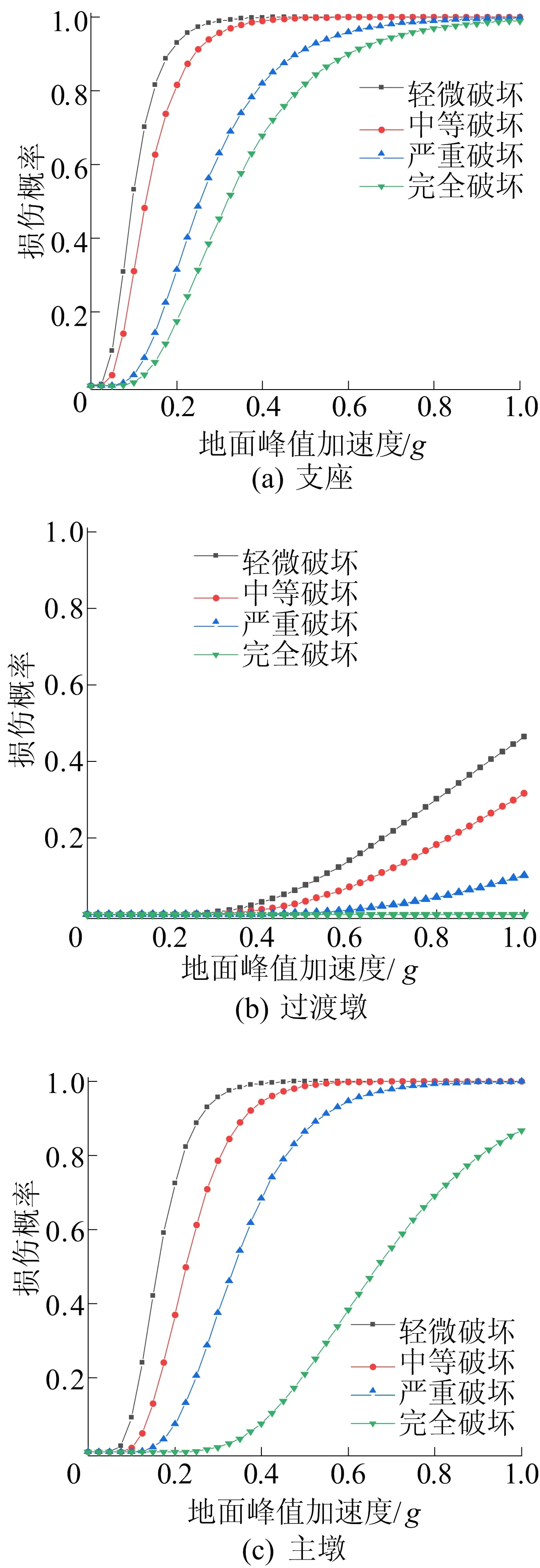
图6 3种构件易损性曲线

从图6可以看出:在PGA为0.1g时,支座发生轻微破坏和中等破坏的概率分别为53.2%、31.1%,发生严重破坏和完全破坏的概率分别为3.0%、1.0%;主墩发生轻微破坏和中等破坏的概率分别为9.3%、1.2%,发生严重破坏和完全破坏的概率为0;过渡墩未发生任何状态的破坏。在4种损伤状态下,支座的损伤超越概率均最大,表明支座是最容易发生破坏的构件。值得一提的是,虽然不同构件在不同损伤状态下的损伤超越概率均随着PGA的增加而增加,但其各自增长速率不同。易损性曲线增速的快慢能够在一定程度上反映构件抗震延性的强弱。支座发生轻微、中等破坏概率的增速较快,发生严重、完全破坏概率的增速较慢;主墩发生轻微、中等和严重破坏概率的增速相差不大,发生完全破坏概率的增速较慢;过渡墩易损性曲线的增速均较慢。综合考虑损伤发生难易程度和抗震延性强弱,支座均为抗震能力最差的构件,其次为主墩,而过渡墩的抗震性能较好,在不同强度的地震作用下发生完全破坏的概率均较低。

3.2 桥梁系统易损性曲线

桥梁作为一个由若干构件有机组合而成的复杂结构系统,单一或部分构件的破坏或损伤往往不能够代表整个桥梁系统的破坏或损伤。已有研究结果表明,若以单一构件的破坏或损伤来代替桥梁系统的破坏或损伤,则会高估桥梁系统的抗震能力。因此,若要更加全面地评估桥梁系统在不同强度地震作用下的损伤状态,则需找到一种能够合理反映桥梁构件与桥梁系统之间关系的数学模型。

由于一阶界限法便于理解和使用,被广泛应用于实际工程中,本文采用一阶界限法验证Copula函数建立易损性曲线的合理性。当桥梁结构系统为串联系统,且各个构件之间的失效模式为正相关时,一阶界限法估计的桥梁系统失效概率Psys可表示为:

(7)

其中:i=1,2,…,n;Pi为构件失效概率;n为研究范畴内构件总数。

由式(3)可知,当系统中有3个构件时,系统失效概率公式为:

Psys=P1+P2+P3-C(P1,P2)-C(P1,P3)-

C(P2,P3)+C(P1,P2,P3)

(8)

Copula函数种类众多,采用Akaike信息准则(Akaike information criterion,AIC)可对Copula函数进行优度比选[13]。轻微破坏状态下,支座与过渡墩之间的17种Copula函数优选结果如图7所示。

图7 轻微破坏下支座与过渡墩之间的Copula函数优选结果

图7中,180Copula函数为其对应Copula函数旋转所得,Copula函数与180Copula函数之间的关系见文献[20],Copula函数的表达式见文献[10]。

根据AIC,模型的拟合优度值越小,表明拟合效果越好。从图7可以看出,在轻微破坏状态下,支座与过渡墩之间的Copula函数中,Student Copula函数的拟合优度值最小,因此采用Student Copula函数。支座与过渡墩的Student Copula函数的图像如图8所示。图8中,P支座、P过渡墩分别为支座、过渡墩轻微破坏的概率。采用AIC计算得到轻微破坏状态下各构件之间的最优Copula函数,见表5所列。表5中:参数1表示构件之间的相关程度;参数2为Copula函数的自由度。

表5 轻微破坏下构件之间最优Copula函数及其参数

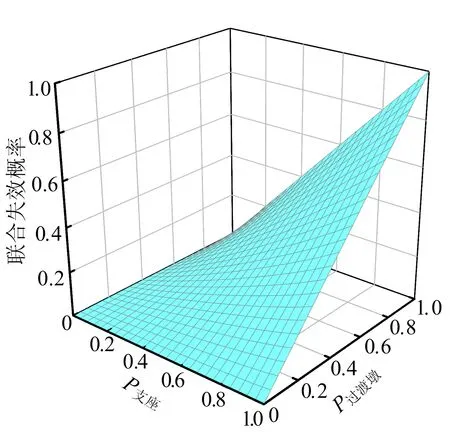
图8 轻微破坏下支座与过渡墩Student Copula函数图像

在获得各构件之间的最优Copula函数后,将单个构件的损伤概率代入对应的Copula函数,即可得到构件之间联合失效概率。将单个构件的损伤概率和构件之间的联合失效概率代入式(8)可得系统的失效概率。在4种损伤状态下,由Copula函数与一阶界限法计算所得系统易损性曲线的对比如图9所示。

图9 4种损伤状态下桥梁系统2种方法易损性曲线对比

从图9可以看出,在4种损伤状态下,由Copula函数计算得到的系统失效概率处于一阶界限法计算结果的包络范围内,验证了采用Copula函数建立系统易损性曲线的合理性。在轻微、中等、严重和完全破坏4种损伤状态下,由Copula函数计算所得的失效概率与一阶界限法下界的最大差值分别为0.7%、0.6%、2.5%、1.4%,与一阶界限法上界的最大差值分别为7.8%、6.8%、14.3%、2.6%。从一阶界限法的计算公式可知,上、下界分别表示构件之间完全不相关和完全相关情况下的系统失效概率。采用Copula函数计算得到的系统失效概率与下界的差值较小,表明构件之间的相关性较强,若采用下界表示系统失效概率,则会在一定程度上高估桥梁的抗震能力。

4 结 论

本文针对常见混凝土矮塔斜拉桥进行地震易损性分析,采用均匀设计法与神经网络相结合的方式建立构件易损性曲线,并引入Copula函数计算基于串联模型的桥梁系统易损性曲线,得到如下结论:

1) 对于构件易损性,在本文研究的支座、过渡墩和主墩3种构件中,支座在地震作用下最容易发生破坏,应给予重点关注;其次易出现破坏的构件为主墩,相较于轻微、中等、严重破坏,主墩发生完全破坏的概率较低;过渡墩出现破坏的概率最低,为安全储备最大的构件,具有良好的抗震能力。

2) 对于系统易损性,采用Copula函数计算所得的系统易损性曲线介于一阶界限法的上、下界之间,验证了该方法计算易损性曲线的正确性。采用Copula函数计算所得系统失效概率与一阶界限法上、下界差值最大分别为14.3%、2.5%,显然更接近一阶界限法的下界,表明桥梁系统各构件之间具有较强的相关关系。

3) 作为一种求解联合分布函数的重要方法,Copula函数适用于受力较复杂的矮塔斜拉桥结构。采用该方法能够获得较精准的系统失效概率值,而非一阶界限法所得的失效区间,可为工程抗震评估和结构设计人员提供有价值的参考。