非饱和土-结构动力响应的2.5维有限元-完美匹配层法

狄宏规，苏光北，郭慧吉，周顺华，于佳永

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室，上海 201804；3.上海申通地铁集团有限公司技术中心，上海 201103)

地铁给城市居民的出行带来极大便利,但近年来地铁运行产生的环境振动问题也愈发突出。地下铁路行车振动经由轨道、隧道以及土体向外传播,进一步诱发邻近建(构)筑物的二次振动和噪声,严重影响邻近建筑物内居民的生活、周边精密仪器等的正常工作以及邻近古建筑安全等。因此,地铁减(隔)振问题正受到越来越多的关注[1-2],为揭示车致振动传播机理,提出有效减(隔)振措施,首先需要建立可靠的地基-隧道动力响应分析模型。

常见的地基-隧道动力响应预测解析(半解析)模型有嵌入的欧拉梁模型[3-4]、管中管(PiP)模型[5-6]及波面转化法[7-8]等。解析(半解析)模型计算效率较高,能够了解振动传播的一般规律,但无法处理不规则边界。难以考虑复杂地基结构,不便用于减(隔)振设计。与解析(半解析)模型相比,数值模型的优势在于可以进行精细化建模,模型适应性更广。常见的有2维、3维[9-10]、2.5维[11-12]、周期性有限元模型[13]等。然而有限元模型计算效率相对较低,且需要截断无限域,存在较大计算误差。为此相关学者基于2.5维动力Green函数,提出边界元来截断无限域,构建2.5维有限元-边界元模型[14-15]、周期性有限元-边界元模型[16]等。但边界元由于引入边界积分处理,损失部分计算效率,所以需要更好的边界处理方法[17]。Bérenger[18]引入复数坐标下的拉伸函数,构建可以完全吸收各个方向、各种频率波的完美匹配层(Perfectly Matched Layer, PML)单元。近年来,完美匹配层法被用于结构动力分析的边界处理当中[19-20],可以兼顾模型计算精度与计算效率。然而,上述既有的数值模型仅将土体视为单相弹性或两相饱和多孔介质,尚未考虑地基土体的三相特性。

为此,本文基于非饱和土运动微分方程、连续性方程以及渗流运动方程,结合应力、渗流边界条件,采用 Galerkin法,推导出频域内ub-pl-pg格式2.5维有限元方程。同时引入拉伸函数构建PML处理边界,提出非饱和地基-结构动力响应分析的2.5维有限元-完美匹配层方法。基于该方法,研究某工程地铁盾构隧道并行高铁路基段隔离桩的减振效果,研究结果可为轨道交通的减振设计提供参考。

1 非饱和地基土-结构动力响应的2.5维有限元

首先定义时间t到频率ω、轴向坐标z到波数kz的双重Fourier变换,即

( 1 )

式中:ω为时间t对应的频率;kz代表坐标z对应的波数;上标“～”、“-”分别为频域、波数域;i为虚数单位。

将地基土体视为由固、液、气组成的三相介质,参考文献[8]中非饱和地基土波动方程求解过程,可得频域内非饱和地基土运动微分方程、连续性方程、渗流运动方程分别为

( 2 )

( 3 )

( 4 )

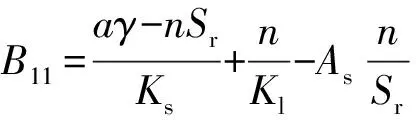
整理式( 4 )可得

( 5 )

式中:M1、Mg为计算参数,Ml=iωnSrρlg/kl,Mg=iωn·(1-Sr)ρgg/kg。

将式( 5 )代入式( 2 ),结合式( 3 )可得非饱和土振动控制方程为

( 6 )

引入应力、渗流边界条件,即

( 7 )

式中:σij为土体单元总应力分量;nj为应力与形式平面法线同方向夹角的余弦值;f、cl、cg分别为边界处的外力以及边界处输入的液体、气体流速。

结合式( 7 ),利用Galerkin法处理式( 6 )可得

( 8 )

式中:V为计算区域的体积;S为计算区域的外表面。

根据分部积分原理得

( 9 )

将式( 9 )、式( 5 )代入式( 8 )得

(10)

式中:cij为计算参数,i=1,2,3,j=1,2,3,4,5,6。计算式分别为

Mg/(Mg-ω2ρg)

c12=nSrρl(Ml-ω2ρl)-1

c13=n(1-Sr)ρg(Mg-ω2ρg)-1

c21=Sr(1-n-Kb/Ks)c22=nSrMl/(Ml-ω2ρl)

c24=nSr/(Ml-ω2ρl)c26=0

c31=(1-n-Kb/Ks)(1-Sr)

c32=n(1-Sr)Mg/(Mg-ω2ρg)

根据固体位移、液体孔压性质以及有效应力原理,可得各物理量矩阵表达式

(11)

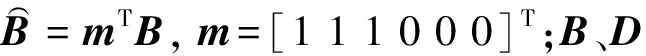
将式(11)代入式(10),并结合式( 1 )进行z向的Fourier变化,可得到ub-pl-pg格式的非饱和地基2.5维有限元表达式为

(12)

式中:Kij、Lij、Gij分别为刚度矩阵、溶体贡献矩阵,气体贡献矩阵,i=1,2,j=1,2。计算式分别为

K11=-(B*N)TDBN|J|dηdζ

K12=ω2c11NTN|J|dηdζ

对于非饱和地基中的路基和隧道结构,在建模时均简化为单相弹性介质,求解其2.5维有限元格式时,只需将前述三相介质的波动方程退化为单相弹性介质的波动方程,退化方法参考文献[21],此处不再赘述。

2 完美匹配层边界

(13)

弹性波在传播过程中可分为传播波(Propagating)与隐逝波(Evanescent),因此定义拉伸函数λ(s)[22]为

(14)

式中:a0为无量纲频率常数,a0=ωLPML/cs,LPML为PML区间长度,ω为角频率,cs为剪切波速;fe为主要衰减隐逝波的拉伸函数;fp为主要衰减传播波的拉伸函数,其定义分别为

(15)

其中,f0e、f0p、q均为拉伸多项式优化参数,f0p为主要衰减弹性波波长,f0e为主要衰减弹性波幅值。因此选取合适的f0e、f0p、q可实现有限单元中弹性波迅速的衰减。

根据式(13)坐标拉伸定义,可得其导数形式为

(16)

将式(16)代入式(12)推导过程中,可得完美匹配层有限元表达式

(17)

式中:

通过Matlab软件自编代码求解式(12)、式(17),可得到方程在频域-波数域内的解,对其进行快速傅里叶逆变换(Fast Fourier Transform)得到时间-空间域的解。Fourier 逆变换点数N=524,步长间隔取1 m。当计算机为AMD R9 3950X 的CPU和64 GB运行内存时,每个波数下计算时间在70 s左右。

3 隔离桩减振效果分析

3.1 模型验证

为验证模型的可靠性,将本文模型的计算结果与文献[21]给出的解析模型进行对比,验证模型见图1。图1中,模型长14 m,宽17 m,隧道外径D=6 m,衬砌厚度e=0.25 m,隧道中心线距地表距离H0=10 m,PML边界厚度1 m,f0e=0,f0p=20,q=1[22]。计算中非饱和土以及隧道参数参考文献[21],见表1。非饱和地基-隧道模型在单位简谐荷载(f=30 Hz,v0=0 m/s)作用下,隧道底部(x=0,y=-3)竖向动位移沿隧道轴向的分布规律见图2。由图2可知,由于有限元网格尺寸选取对计算精度有一定影响,与文献[21]中的结果相比,本文结果在部分区间存在轻微波动,但总体趋势和量级一致,验证了本文模型的可靠性。

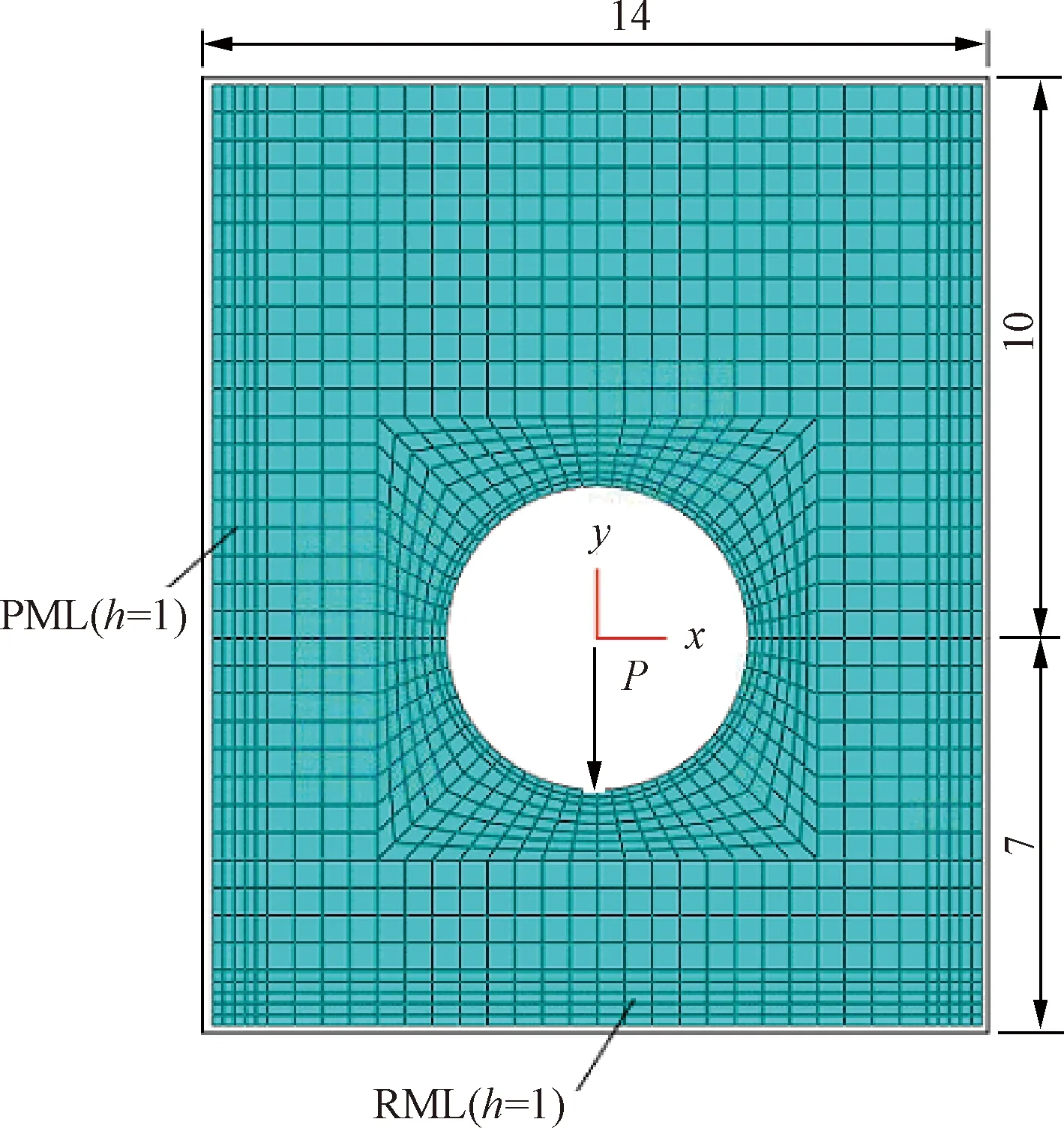
图1 验证模型平面图(单位:m)

图2 隧道底部(x=0,y=-3)竖向动位移沿隧道轴向的分布规律

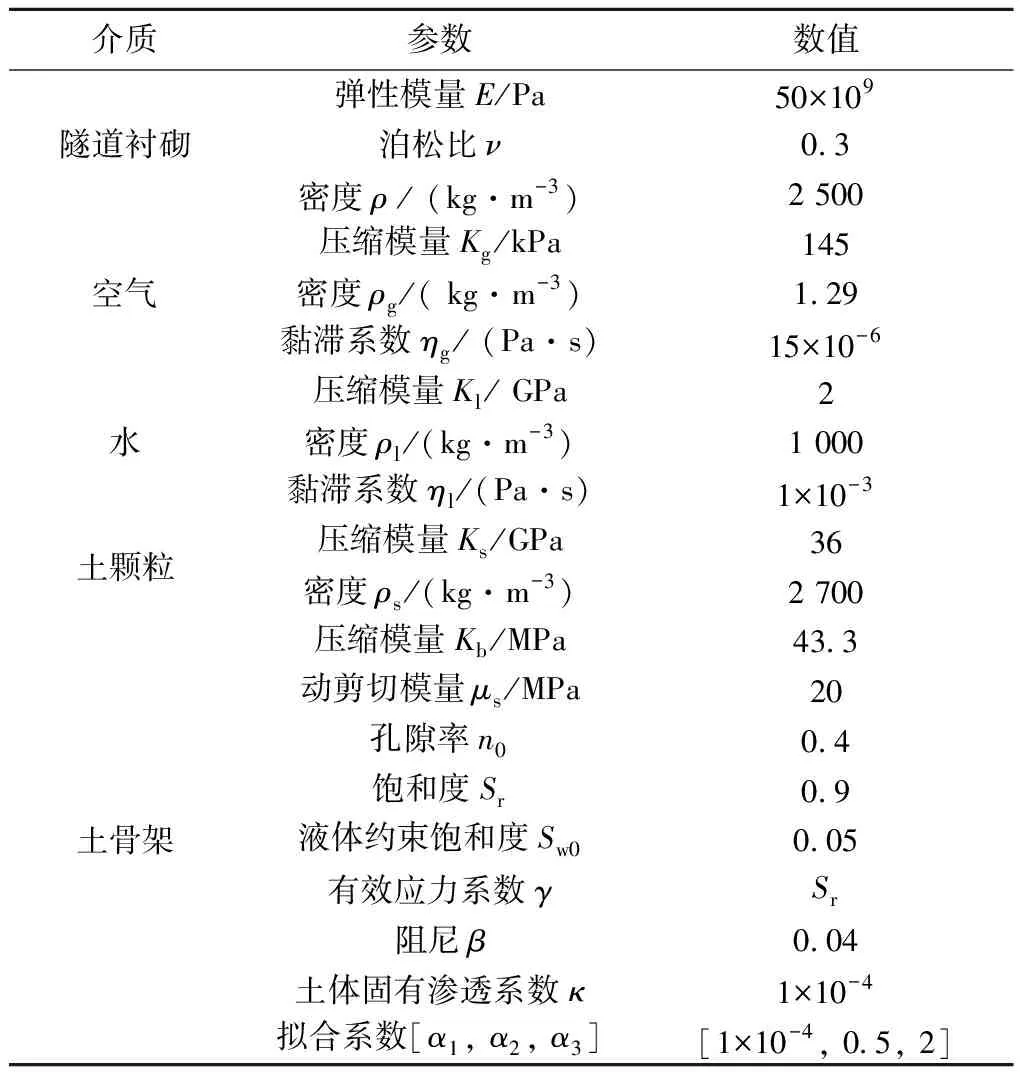
表1 验证模型计算参数取值[21]

3.2 算例分析

以某地铁隧道并行高铁路基段为工程背景,开展隔离桩隔振效果分析,模型简化示意见图3。图3中,模型总长40 m,高25 m,隧道中心距离地表H0=15 m,隧道外径11 m,内径10 m,衬砌厚度0.5 m,隧道埋深9.5 m,路基高度2 m,路基宽度10 m,路基坡度为1∶1,路基坡角与隧道间距9.5 m。PML边界厚度1 m,相关常数取值:f0e=0,f0p=20,q=1[22]。为保证一个波长内有6个单元以上,每个单元尺寸取为0.5 m×0.5 m,并在靠近隧道处进行网格加密处理。地基土体为砂土,计算参数[23]见表2。隧道衬砌、路基以及隔离桩计算参数见表3。研究隧道仰拱处作用单位移动荷载下(v0=16.7 m/s,f=0 Hz)非饱和地基中隔振桩的隔振效果。

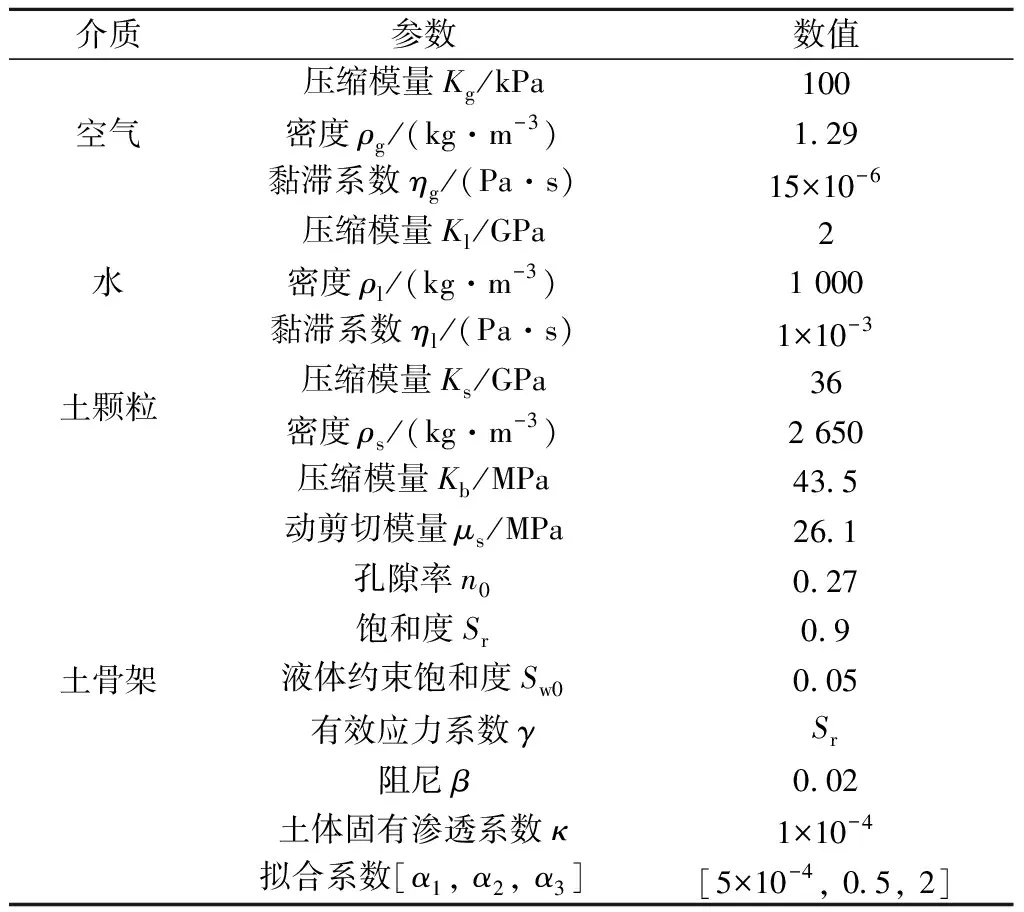
表2 非饱和地基土体计算参数[23]

表3 单相弹性体计算参数

3.3 隔振效果及参数影响

(1)不同隔离桩桩径d和桩阻尼的隔振效果

在距离隧道L=1.5 m处设置单排隔离桩,桩长24 m,桩径d依次取0、0.8、1.0、1.2 m。在不同桩径下,模型上表面沿y方向动位移幅值Uy见图4。由图4可知,设置隔离桩可以有效减小地基表面的振动响应,并且桩径越大,隔离桩的隔振效果越好。增大隔离桩桩径对桩后侧(隧道侧)土体的隔振效果要优于桩前侧(路基侧)。此外发现隔离桩的存在会使得隧道右侧(无隔离桩侧)的土体响应增强。

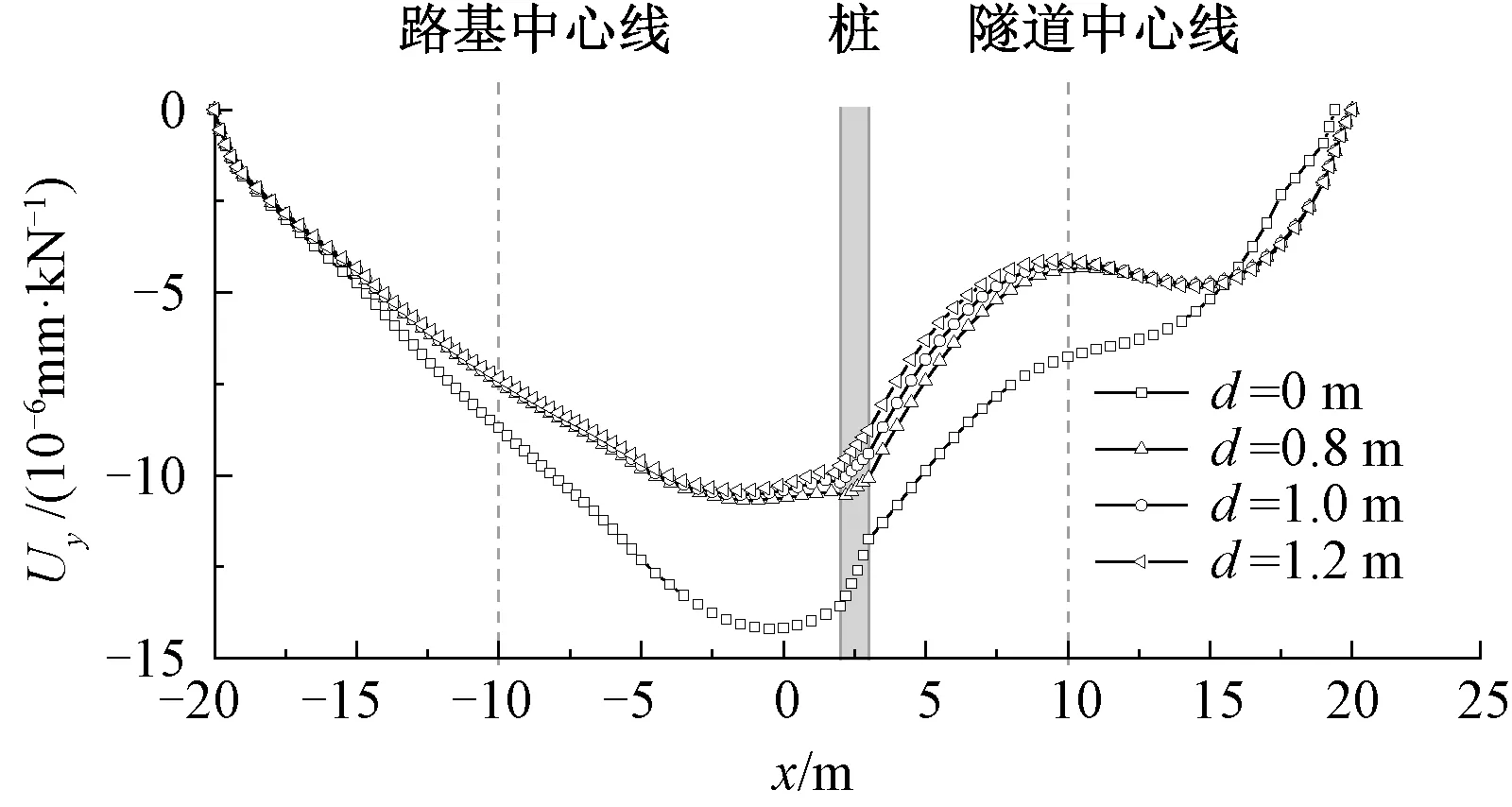
图4 不同桩径下地基上表面的振动响应

在距离隧道L=1.5 m处设置桩径d=1 m,桩长24 m的单排隔离桩。隔离桩阻尼β依次取0.015、0.030、0.045,同时设置附加工况d=0 m(无隔离桩)。在不同隔离桩阻尼下,模型上表面沿y方向动位移幅值Uy见图5。由图5可知,随着桩阻尼的增大,地基表面振动响应变化较小。可见该移动荷载作用下,改变阻尼对隔离桩的隔振效果影响较小。

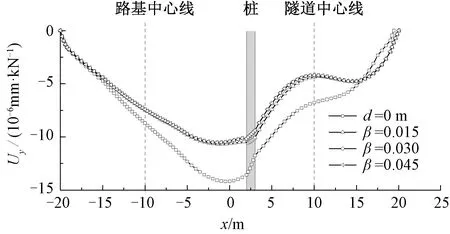
图5 不同桩阻尼下地基上表面的振动响应

(2)不同间距L(桩与隧道之间的距离)的隔振效果

取隔离桩桩径d=1 m,桩长24 m,桩与隧道间距L依次取1.5、3.0、4.5 m,附加工况d=0 m(无隔离桩)。在不同桩与隧道间距下,模型上表面沿y方向动位移幅值Uy见图6。由图6可知,增大桩与隧道间距L可以降低地基上表面的振动响应。且L越大,桩前侧(路基侧)的振动响应越小,桩后侧(隧道侧)的振动响应变化较为复杂,不同桩与隧道间距均能减小桩后侧的土体振动响应,但与L=3.0 m相比,L=4.5 m时桩后侧振动响应反而更大。说明增大的L能够减小桩前侧的振动响应,但是对于桩后侧(隧道侧)的振动响应,较大的L并不能取得更好的隔振效果。改变L,隧道右侧(无隔离桩侧)的土体响应增强现象发生变化,L越大,增强区的增强效应越明显,增强区范围越大。

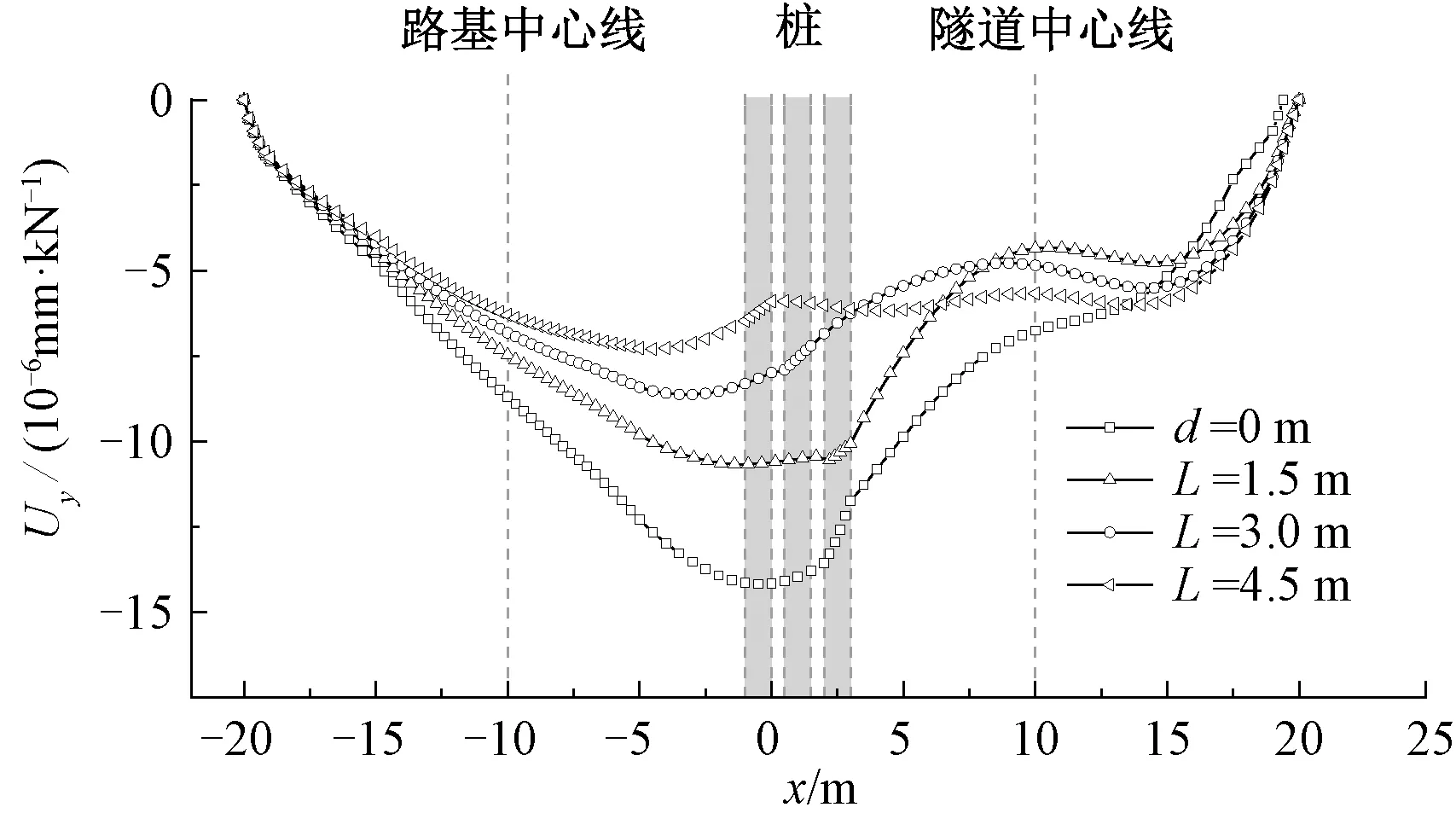
图6 不同桩与隧道间距下地基上表面的振动响应

(3)不同隔离桩排数与排桩之间的距离S的隔振效果

在距离隧道L=1.5 m处设置桩径d=1 m,桩长24 m的隔离桩。隔离桩取单排(S=0 m)和双排,在双排桩情况下,两排桩之间的距离S依次取3 、5 m,附加工况d=0 m(无隔离桩)。在不同隔离桩排数与排桩之间的距离S下,模型上表面沿y方向动位移幅值Uy见图7。由图7可知,双排桩的隔振效果要优于单排桩,且S越大,双排桩的整体隔振效果越好,桩间土体振动响应会略有增加,但仍小于单排桩情况下该区域的振动响应。

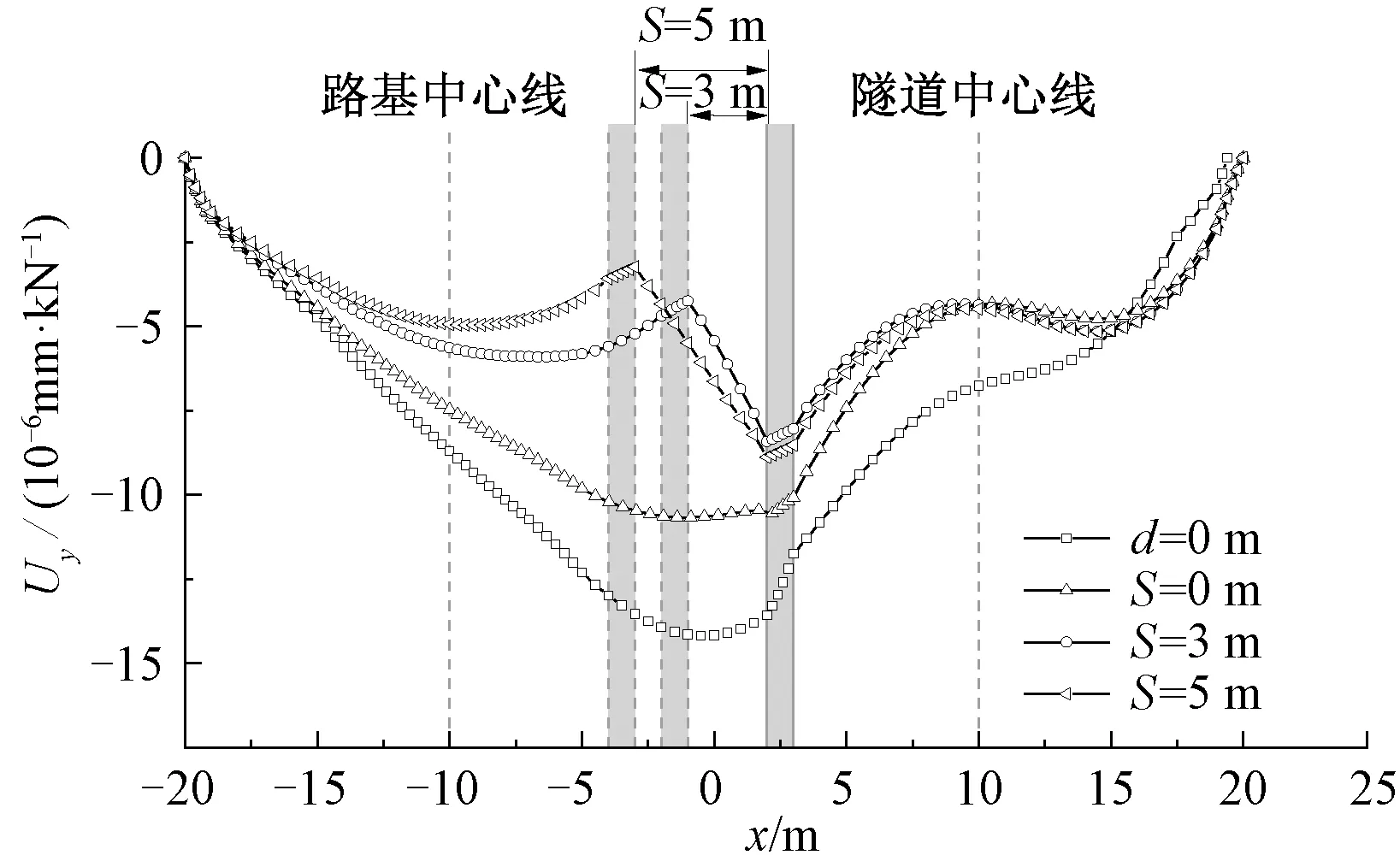
图7 不同隔离桩排数下地基上表面的振动响应

4 结论

(1)基于非饱和土实用波动方程,推导ub-pl-pg格式的非饱和地基2.5维有限元表达式,结合拉伸函数构建PML边界单元,提出非饱和地基-结构动力响应的2.5维有限元-完美匹配层法。将该方法的计算结果与既有解析法的计算结果相对比,验证该算法的可靠性。

(2)通过参数退化,本文算法中的三相介质(非饱和地基土)可退化为两相介质(饱和地基土)或单相介质(单相弹性地基土)。因此,本文算法也可用于非饱和土、饱和土、单相弹性地基土共存时层状地基地铁隧道系统的动力响应分析。

(3)算例分析表明,隔离桩具有良好的减振效果,并且桩径越大、距离隧道越远,隔离桩的减振效果越好,双排桩的减振效果要优于单排桩。但受本文算法纵向几何尺寸不变性假设的限制,隔离桩只能视作咬合桩,无法考虑桩间距,即本文算法无法考虑地基土体和结构沿线路纵向的变化特性。