“一日一图”模式下高速列车开行方案与票额分配协同优化方法
赵 翔,武晋飞,单杏花
(中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081)
高速铁路(以下简称“高铁”)客流变化受周次、季节、节假日、天气、突发事件等多种因素影响,不同时期客流需求可能存在明显差异。以往主要利用票额分配方法应对每日变化的客流需求。然而,票额分配仅能调整席位资源的运用,不能改变列车的开行属性,其调整空间和协调能力具有一定的局限性。为了避免客流高峰时期运力资源紧张、低估时期运力资源浪费,中国国家铁路集团有限公司(以下简称“国铁集团”)提出“一日一图”运输组织模式、每日列车开行方案动态调整,以适应不同时期的客流变化。
列车开行方案优化和票额分配调整均是实现铁路运力资源合理配置的重要方法。列车开行方案在车辆资源层面对列车运行径路、开行频率、停站方案等内容进行优化;票额分配在席位资源层面对坐席在不同OD间的分配数量进行调整。因铁路运输组织时空约束复杂,需经历列车开行方案优化、列车运行图编制、动车组运用计划编制、乘务计划编制、票额分配调整等多个阶段才能形成最终的运输方案。因此,既有列车开行方案优化和票额分配调整是在运输组织的不同阶段进行优化。文献[1]均衡考虑铁路收益和旅客需求,构建开行方案优化双层规划模型;文献[2]基于列车“备选集”优化京沪高铁及相关路网开行方案;文献[3]研究列车开行方案与运行图组合优化方法;文献[4]考虑旅客出行时变需求建立了高铁列车开行方案优化模型;文献[5]考虑旅客出行选择行为研究了基于开行方案的客流分配寻路算法。文献[6]基于潜在类别模型研究铁路收益管理问题;文献[7]研究随机需求下考虑旅客选择行为的动态票额分配方法;文献[8]构建高铁多列车票额分配模型;文献[9]提出考虑旅客选择偏好的票额分配方法;文献[10-12]研究票价和票额分配综合优化问题。上述研究主要是在售票组织前研究列车开行方案优化问题,或是在开行方案给定下研究票额分配问题,没有将开行方案优化和票额分配问题结合考虑。文献[13]尝试将开行方案优化与收益管理问题结合研究,但未考虑“一日一图”背景下的实际路网问题。既有研究将列车开行方案和票额分配在运输组织的不同阶段分别优化可能存在以下问题:①票额分配阶段主要调整席位资源的运用,无法改变列车的开行属性,其调整空间和协调能力有限。当客流需求变化较大时,调整效果较差,可能造成客流需求流失或席位资源浪费。②开行方案优化阶段对坐席在不同OD的具体利用情况考虑不足,票额分配阶段需要重新调整席位运用,调整结果可能在一定程度上偏离开行方案设计的初衷,无法实现开行方案的预期效果。综上所述,在“一日一图”背景下,综合考虑列车开行方案和票额分配更有利于铁路整体运力资源的合理配置以适应不同时期的客流需求变化。
为此,本文基于每日变化的客流需求,研究“一日一图”模式下列车开行方案与票额分配协同优化方法。鉴于构建模型为非线性规划,设计一种遗传算法进行求解。对我国真实高铁路网进行案例分析,与开行方案给定下的票额分配方法进行对比。
1 “一日一图”运输组织模式下“流-车-票”问题一体化编制思路
我国高铁路网规模庞大、时空约束复杂,运输计划的编制需要经历多个环节,各环节彼此依存且相互制约。例如,开行方案中安排的列车停站需要在运行图编制时确定具体的到发时刻,运行图编制难以解决的运行冲突可能需要在开行方案中重新调整。同时,高铁运输网络是一个系统性整体,一个节点运输计划的调整往往导致相邻节点甚至整个网络的运输计划改变。因此,尝试频繁调整运输组织的多个环节实现“一日一图”的设想可能面临巨大困难。
目前,国铁集团每年经历4次季度调图。在季度调图期间,会编制日常线、周末线、高峰线等不同开行规律的旅客列车开行计划,以满足不同时期的客流变化。其中,日常线列车每日固定开行,周末线和高峰线列车根据客流变化进行增开或停运。因为上述列车的开行特征已经确定且满足运行图编制中的所有约束,所以增开或停运上述列车不需要过多调整其他运输计划,很大程度上降低了每日方案调整的复杂度,提高了每日方案调整的可行性。考虑上述实际,本文基于季度调图的基本方案,将旅客列车分为固定开行列车(如日常线)和非固定开行列车(如高峰线)两类。基于不同时期的客流变化,对非固定开行列车的开行计划和所有列车的票额分配计划进行一体化编制。
2 模型构建
2.1 问题描述
(N,I)为有|N|个车站和|I|个区段高铁路网,其中:N为车站集合,N={1,2,…, |N|};I为区段集合,I={1,2,…, |I|};i为连接相邻车站的任意轨道路段,i∈I。
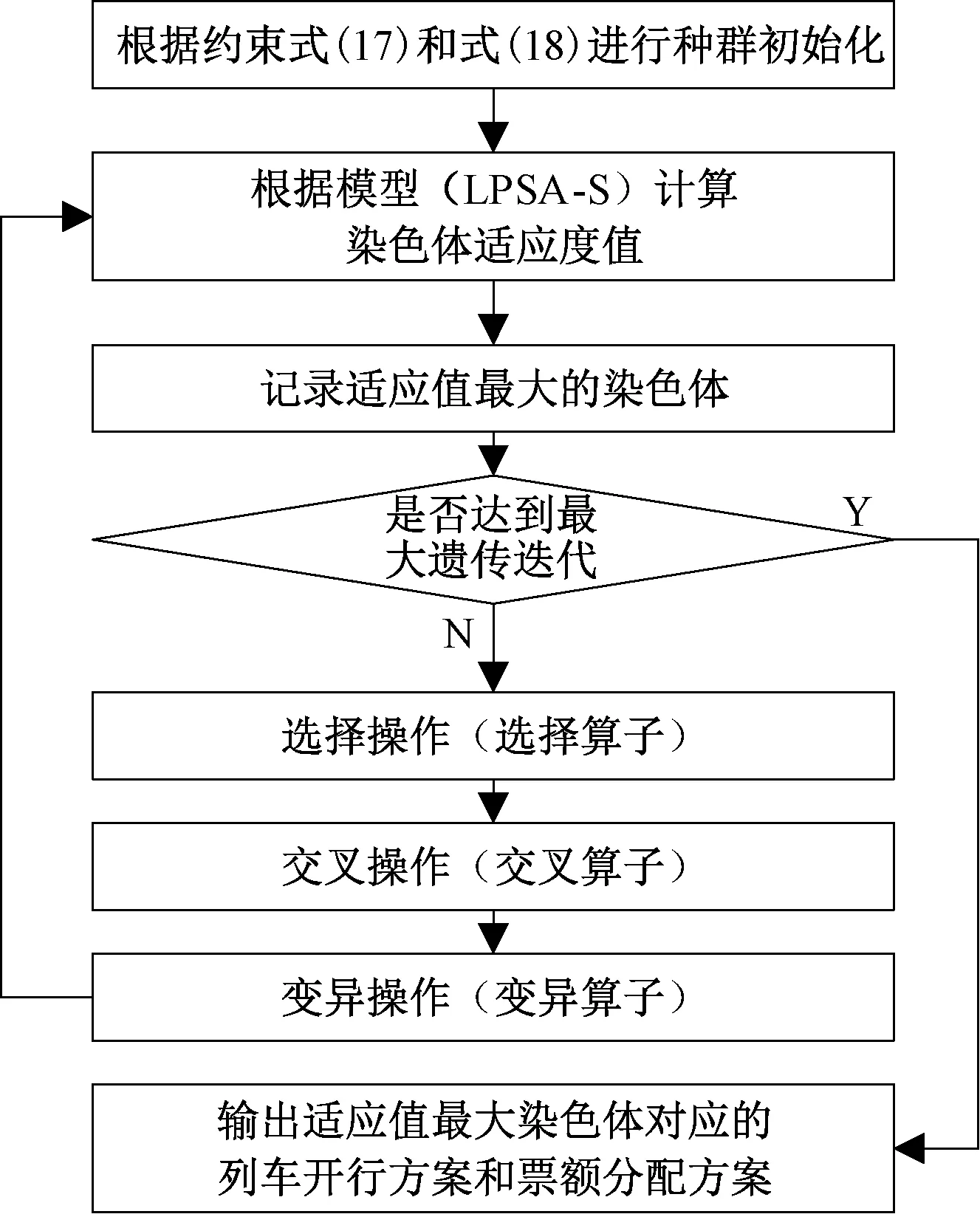
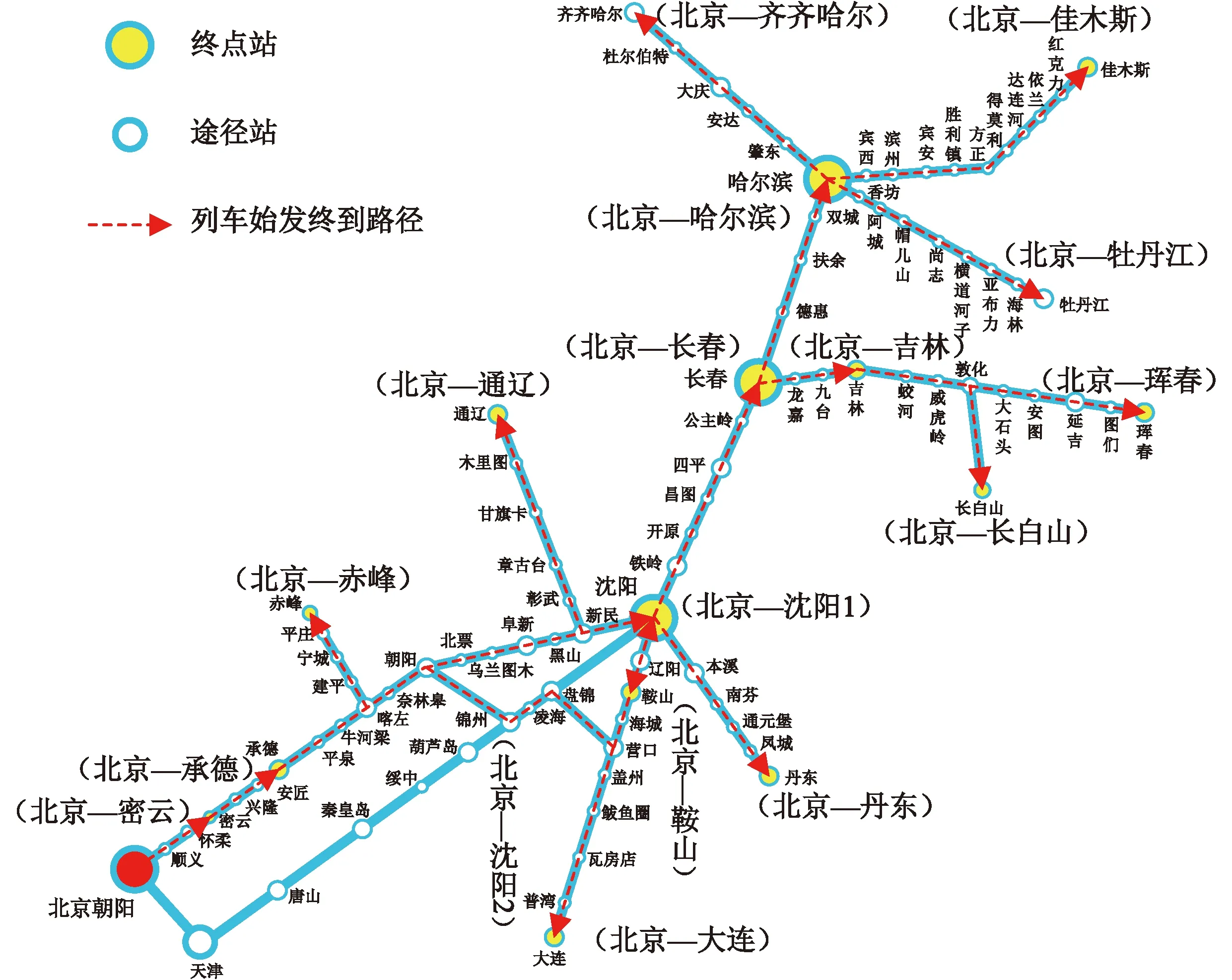
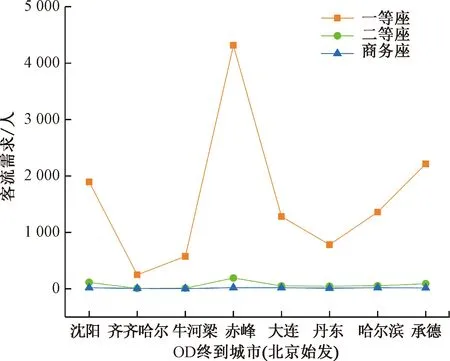
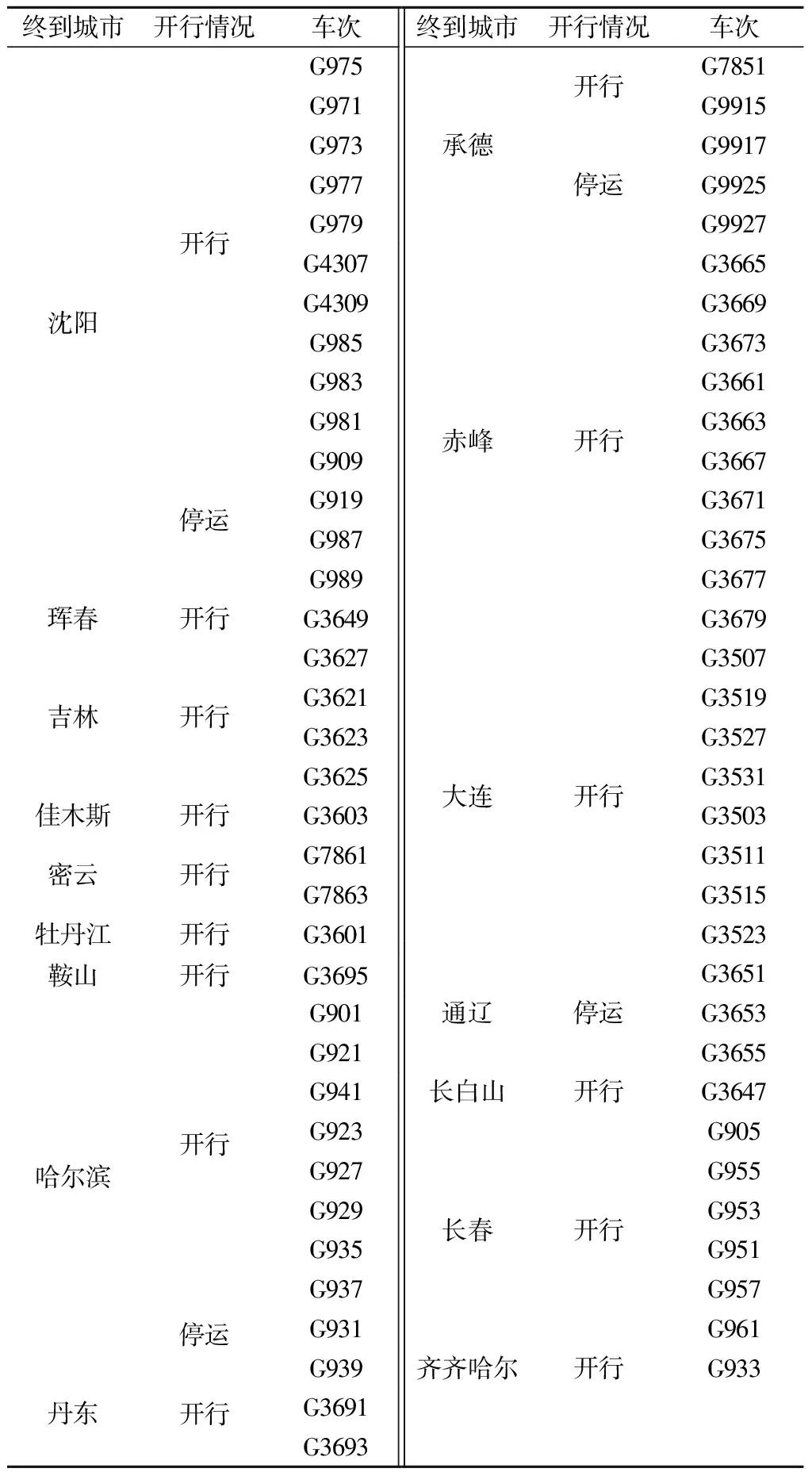
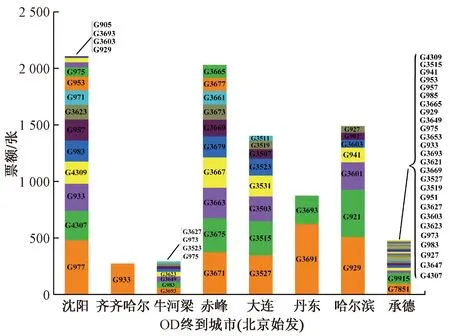
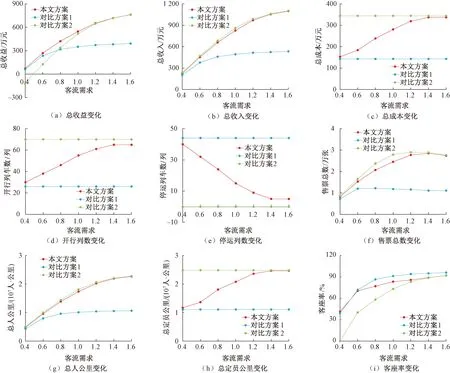
J为高铁路网所有OD(路径)的集合,J={(o,d):o∈N|N|,d∈N1,o W为席位等级集合;w为任意席位等级,w∈W。 rg为0-1决策变量,列车g开行为1,停运为0。bg,j,w为列车g在OD对j席位等级w提供的票额数量,为决策变量。列车g在OD对j席位等级w可以提供的票额数量为rgbg,j,w。集合G中所有列车在OD对j席位等级w可以提供的总的票额数量为 ( 1 ) 当OD对j席位等级w的客流需求为xj,w时,集合G中所有列车在OD对j席位等级w的客票销售数量为 ( 2 ) pj,w为OD对j席位等级w的车票销售价格,集合G中所有列车在OD对j席位等级w的客票销售收入为 Rj,w(rg,bg,j,w)=pj,w·Sj,w(rg,bg,j,w) ( 3 ) 集合G中所有列车的总的客票销售收入为 ( 4 ) 高铁运营需要进行发到、运行、动车组检修、轨道线路、供电及通信、车站服务等多种作业,各项作业均有一定的支出。为估算各列车开行成本,借鉴文献[14]采用的作业成本法计算各列车开行成本,包括发到作业成本、列车运行作业成本、列车检修作业成本、轨道线路作业成本、供电及通信作业成本、站舍服务作业成本。列车g开行成本为 δ3·lg+δ4·dg+δ5·lg+δ6·qg ( 5 ) qg为列车g的发送人数,可利用列车g的票额分配数量进行估计,即 ( 6 ) dg为列车g的总重吨公里,其估算式为 ( 7 ) 根据式( 6 )、式( 7 ),式( 5 )可转化为 (δ3+δ5)·lg ( 8 ) 因此,集合G中所有列车的总的运营成本为 ( 9 ) 中国铁路客户服务中心将客票与席位对应销售,且高速列车不采取超售策略。因此,列车g的可售票额数量受到列车席位能力的约束,即 (10) 式中:cg,w,i为列车g席位等级w在区段i的席位能力;ai,j为0-1变量,表示OD对j与区段i的对应关系,当列车在OD对j的运输途径区段i时,表示OD对j的票额需占用该列车在区段i的席位资源,即ai,j=1,否则为0。 因停站方案差异,各列车只能服务其停站之间的OD。θg,j为0-1变量,表示列车g与OD对j的对应关系。当θg,j=1时,表示列车g停靠OD对j的起始站和到达站,即列车g能够提供OD对j的客运服务,此时,列车g可以为OD对j分配票额,分配数量可以大于0,也可以等于0,即bg,j,w≥0。当θg,j=0时,表示列车g未停靠OD对j的起始站或到达站,即列车g不能提供OD对j的客运服务。此时,列车g不能为OD对j分配票额,即bg,j,w=0。因此,列车g在OD对j席位等级w提供的票额数量受到如下约束 (11) 将式(11)转化为如下线性约束形式 (θg,j-1)bg,j,w=0 ∀g∈Gj∈Jw∈W (12) 在式(12)中,当θg,j=1时,θg,j-1=0。此时,bg,j,w为任意值均能保证(θg,j-1)bg,j,w=0,又因为bg,j,w∈N,所以bg,j,w≥0。当θg,j=0时,θg,j-1=-1。此时,因为(θg,j-1)bg,j,w=0,所以bg,j,w=0。通过上述论证,式(11)与式(12)等价,且式(12)为更易于处理的线性约束。 (13) 基于预测每日OD客流需求,以提高铁路客票收入和降低运营成本为目标,考虑列车席位能力约束,建立高速列车开行方案与票额分配协同优化模型(LPSA) (14) s.t. (15) (θg,j-1)bg,j,w=0 ∀g∈Gj∈Jw∈W (16) (17) (18) bg,j,w∈N∀g∈Gj∈Jw∈W (19) 本文构建的开行方案与票额分配协同优化模型为非线性整数规划,已有精确算法不能很好地求解。遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法,适合处理大规模非线性优化问题。本文设计一种遗传算法求解上述模型。 选取列车开行决策变量(rg)作为基因。每一条染色体表示一组列车开行方案。根据式(17)和式(18)随机生成初始染色体 (20) 当票额分配数量超过旅客需求时,超出需求的票额不会额外增加客票收入。因此,根据预测需求,增加票额分配约束 (21) 根据式( 2 )和式(21),客票销售数量可做如下变换 (22) 基于式(21)和式(22),将染色体γm对应的各列车开行方案代入模型(LPSA),可转化为以下模型(LPSA-S) (δ3+δ5)·lg (23) s.t. (24) (25) (θg,j-1)bg,j,w=0 ∀g∈Gj∈Jw∈W (26) bg,j,w∈N∀g∈Gj∈Jw∈W (27) 遗传算法包括选择操作、交叉操作和变异操作。选择操作采用轮盘赌法,即基于适应度比例的选择策略。交叉操作是从种群中随机选择两个个体,然后随机确定一个交叉点,将交叉点的染色体片段进行交换,生成两个新的个体。变异操作从种群中随机选取一个个体,选择个体中的一个染色体片段进行变异,变异后的新的基因值是在该基因取值范围内随机选取。算法流程见图1。 图1 算法流程 依据中国铁路2021年第四季度实际使用列车运行图,以北京朝阳站始发开往我国东北三省方向的所有高速列车为研究对象。其中,图定日常开行列车26列为确定开行列车,图定高峰开行列车44列为可停运或增开列车,不同运行径路开行车次见表1。途径线路包括:京哈高铁、哈牡客专、哈齐客专、喀赤客专、新通客专、朝凌高铁、沈丹客专、沈大高速、长珲城际及相关衔接线路。所有列车共停靠84个车站,服务1 098个OD。根据始发终到城市和途径线路,所有列车共有17条始发终到路径,不同运行径路开行车次见图2。 表1 不同运行径路开行车次 图2 不同运行径路途径线站 以2022年12月17日的列车开行方案和票额分配方案为优化目标,基于12306历史销售数据预测各OD客流需求,部分OD的预测客流需求见图3。 图3 部分OD的客流需求 算法中种群规模为40,进化500代,交叉概率0.6,变异概率0.1。借用Python语言编程并调用Gurobi优化器进行建模求解。本文方案基于季度运行图,对每日开行方案和票额分配进行协同优化。本文方案的列车开行情况见表2。 表2 列车开行情况 部分OD各列车的票额分配数量见图4。例如,在服务北京至沈阳的列车中,G977所有等级席位共提供了482张北京至沈阳的票额,为北京至沈阳提供票额数最多的列车。 图4 部分OD各列车的票额分配数量 本文方案总收益545.50万元,开行列车55列,停运列车15列,售票总数2.45万张。目前,我国高速列车开行方案和票额分配在运输组织的不同阶段进行优化。为了验证本文协同优化开行方案和票额分配的优越性,设计两种对比方案。对比方案1:先确定开行方案为开行日常线列车,停运高峰线列车,再对票额分配进行优化;对比方案2:先确定开行方案为开行所有日常线和高峰线列车,再对票额分配进行优化。不同方案下的收益结果及相关指标见表3。表3中,客座率=总人公里÷总定员公里×100%。 表3 不同方案下的收益结果及相关指标 在相同的客流需求下,相比对比方案1,本文方案提高收益195.58万元,提高比例为55.89%。对比方案1在开行方案阶段确定开行列车26列,在票额分配阶段仅能调整开行列车的席位资源,不能增开列车,难以缓解因整体列车资源不足而引起的席位紧张,造成客流需求流失和客运收入减少。相比对比方案2,本文方案提高收益29.00万元,提高比例为5.61%。对比方案2在开行方案阶段确定开行列车70列,在票额分配阶段不能停运列车,难以避免因整体列车资源过剩而引起的席位虚糜,造成整体客座率下降和客运成本增加。因此,相比对比方案1和对比方案2,本文方案通过协同优化开行方案和票额分配,能够更合理地利用列车资源和席位资源。 不同需求强度下不同方案相关指标的变化情况见图5,横坐标客流需求数值如0.8表示初始预测需求的80%。 图5 不同需求强度下不同方案相关指标的变化情况 由图5(a)可知在不同需求强度下,本文方案的总收益均高于对方方案1和对比方案2;所有方案总收益均随着需求的增加而提高;当需求增加时,相比对比方案1,本文方案收益优势逐渐显著;当需求减小时,相比对比方案2,本文方案收益优势逐渐显著。 由图5(b)可知当需求增加时,所有方案的总收入均提高;在任意需求强度下,对比方案2总收入大于本文方案,本文方案总收入大于对比方案1。 由图5(c)可知当需求增加时,本文方案的总成本不断提高;在不同需求强度下,对比方案1和对比方案2的总成本变化很小。 由图5(d)、图5(e)可知当需求增加时,本文方案会增加开行列车数和减少停运列车数;在不同需求强度下,对比方案1和对比方案2的列车开行对数保持不变。 由图5(f)可知在任意需求强度下,对比方案2的售票总数高于本文方案,本文方案售票总数高于对比方案1。随着需求的增加,所有方案的售票总数均呈现先增后微降的趋势,这是因为当席位能力充足时,大部分需求均会被满足,随着需求增加会销售更多的车票;当席位能力紧张时,票额控制策略优先满足长途需求以提高列车席位利用率和运输收益,部分短途需求未被满足,出现了需求增加但售票总量微降的情况。 由图5(g)、图5(h)可知随着需求的增长,所有方案的总人公里均提高,本文方案的总定员人公里不断提高,对比方案1和对比方案2的总定员公里保持不变。 由图5(i)可知随着需求的增加,所有方案的客座率均有提高;在任意需求强度下,对比方案1的客座率大于本文方案,本文方案的客座率大于对比方案2。 本文研究“一日一图”模式下高速列车开行方案与票额分配协同优化方法,根据构建模型特点设计了一种遗传算法进行求解,并与开行方案给定下的票额分配方法进行对比,结果表明:在“一日一图” 模式下,本文方法通过对列车开行方案与票额分配进行协同优化,能够基于变化的客流需求,对列车资源和席位资源进行整体调整,相比开行方案给定下的票额分配方法,能够取得更好的客票收益。 本文提出的列车开行方案与票额分配协同优化方法能够兼容我国现行的运行图调整模式。当每季度列车运行图发生变化时,仅需调整本文模型中开行列车信息就可以完成所需数据的更新。在预售期内,可将已售票列车归入确定开行的列车集合以限制已售票列车的停运调整,从而避免影响已购票旅客正常乘车。然而,本文提出方法没有考虑动车组运用问题,列车开行方案的调整可能会影响后续的动车组运用计划,“一日一图”模式下的动车组运用问题有待进一步研究。此外,列车运营成本的测算是“一日一图”决策的重要基础,列车运营成本的精细化计算方法有待进一步研究。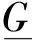
2.2 客票收入
2.3 运营成本
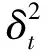
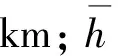
2.4 约束条件
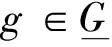
2.5 开行方案与票额分配协同优化模型
3 求解算法
3.1 种群初始化
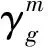
3.2 适应度计算
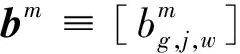
3.3 遗传算子
4 案例分析
4.1 案例背景

4.2 收益分析

5 结论

