Enhanced mechanical and thermal properties of two-dimensional SiC and GeC with temperature and size dependence

Lei Huang(黄磊), Kai Ren(任凯),†, Huanping Zhang(张焕萍), and Huasong Qin(覃华松)

1School of Mechanical and Electronic Engineering,Nanjing Forestry University,Nanjing 210037,China

2Laboratory for Multiscale Mechanics and Medical Science,SV LAB,School of Aerospace,Xi’an Jiaotong University,Xi’an 710049,China

Keywords: two-dimensional,molecular dynamics,mechanical property,heat transport

1.Introduction

By using a micromechanical stripping method,graphene has been successfully separated.[1]Due to their remarkable characteristics and numerous possible applications, twodimensional(2D)materials have garnered extensive attention and research interest.[2,3]For example, graphene has excellent electronic,[4]thermal,[5,6]catalytic,[7]mechanical[8]and magnetic[9]properties.Single-layer graphene’s bipolar electric field effect demonstrates that the charge carriers are more mobile than in semiconductors.[10]Graphene also has high thermoelectric power[10,11]and excellent nonlinear optical characteristics combined with fast response and wide wavelength range in optoelectronic and photonic applications.[12]Inspired by such exciting behaviors of graphene and its successful application in various advanced nanotechnology, research on other 2D materials has been explored.[13]Although they present a large specific surface area, these graphene-like materials possess different mechanical,thermal,electrical,optical and catalytic properties.[14–16]

The electronic, mechanical and thermal performances of the 2D materials have a critical role in the development of atomic devices.For instance, the mechanical properties of borophene are highly anisotropic: in comparison to the armchair direction, the zigzag direction (also known as the buckled direction) has a substantially lower Young’s modulus and fracture strength.[17]The thermal conductance of pure black and blue phosphorene nanoribbons is sensitively affected by edge shape and breadth, and they both have a distinctly anisotropic thermal performance.[18]The mechanical properties of MoS2can determine the fracture strength and fracture strain of MoS2/WSe2lateral heterostructures.These properties are highly temperature sensitive, and when compared to the graphene–hBN heterostructure, the MoS2/WSe2heterostructure exhibits an order of magnitude lower interfacial thermal conductivity.[19]The properties of materials with negative Poisson’s ratio are very necessary for many advanced applications because they typically have enhanced toughness and shear resistance,along with enhanced sound and vibration absorption, such as the puckered atomic structure of singlelayer black phosphorus and B4N monolayer material.Materials that have a negative Poisson ratio are named auxetic materials.They represent an exciting prospect for enhancing mechanical properties and are necessary for many advanced applications.For example, the Poisson ratios of the puckered atomic structure of black phosphorus[20]and B4N[21]are calculated as−0.267 and−0.032, respectively, and these materials can be considered for future nanomechanical devices.Additionally, due to their excellent properties, silicon carbide (SiC) and germanium carbide (GeC) have garnered a lot of interest.[22,23]SiC possesses a large bandgap of about 3.354 eV,[24]a high saturation electron drift velocity (3×107cm/s), a strong electric breakdown field (3×106V/cm),and is used in high-temperature devices suitable for DC to microwave frequencies.[25]SiC is also a potential electromagnetic shielding material and it can be used for electronic packaging of highly integrated circuits, wireless communication,electronic base stations and other electronic equipment.[26,27]Besides,the defects in a SiC monolayer can induce a sizeable spin effect and strong spin–phonon coupling.[28]Furthermore,GeC also acts as a semiconductor with a bandgap of about 2.515 eV,[22]indicating that it is a promising candidate for application in semiconductor devices, crystal diodes, and photovoltaic systems.[29]Due to the exceptional optical performance of 2D GeC, it has undergone substantial research for prospective use in heterostructure devices and solar cells.[30]In comparison to graphene,the mechanical characteristics of a GeC monolayer indicate a low in-plane stiffness(143.8 N/m)and a high Poisson ratio(0.281).[31]Although there have been a large number of studies on the applications of tSiC and GeC monolayers, their mechanical and thermal characteristics are rarely reported and these are crucial properties to explore for further advanced functional nanodevices.

To explore the mechanical characteristics of SiC and GeC monolayers under uniaxial stress in the armchair and zigzag directions,we conduct molecular dynamics simulations(MD)in this work.The impacts of temperature and already-existing fractures on mechanical characteristics are discussed.Additionally,the heat transport capabilities of SiC and GeC monolayers are investigated.Adjustable mechanical and thermal characteristics of SiC and GeC monolayers point to possible usage in nanodevices.

2.Simulation methods

In our work, the zigzag and armchair directions of the SiC and GeC monolayers are oriented along thexandydirections, respectively, as shown in Fig.1.Both the zigzag and armchair directions use periodic boundary conditions, which means a nanosheet structure is obtained.The Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)was used for all MD simulations.[32]It uses OVITO software for structural visualization.[33]To ensure the stability of the values and the correctness of the energy conservation,the time step of all MD simulations is set to 1.0 fs.Initially,the whole system is relaxed at a constant temperature and constant pressure for 200 ps through the Nose–Hoover thermostat.The Tersoff potential,which is often employed and taken into consideration owing to correct parameterization,is utilized to represent the interatomic interactions to achieve agreement with the DFT computations and experimental data.

In the mechanical calculations,all the simulations are performed using a 194.5 ˚A×198.1 ˚A supercell that contains periodic boundary conditions applied in any direction along the plane.Here, the fix/deform method as defined in LAMMPS is used to apply in-plane uniaxial tension with a strain rate of 2×108s−1.The system’s temperature is maintained at a constant level during the tensile deformation process, while the other directions are maintained at zero pressure.During the MD simulations,we examine the normal corresponding forces in the zigzag and armchair directions to obtain the mechanical properties of the two material structures.

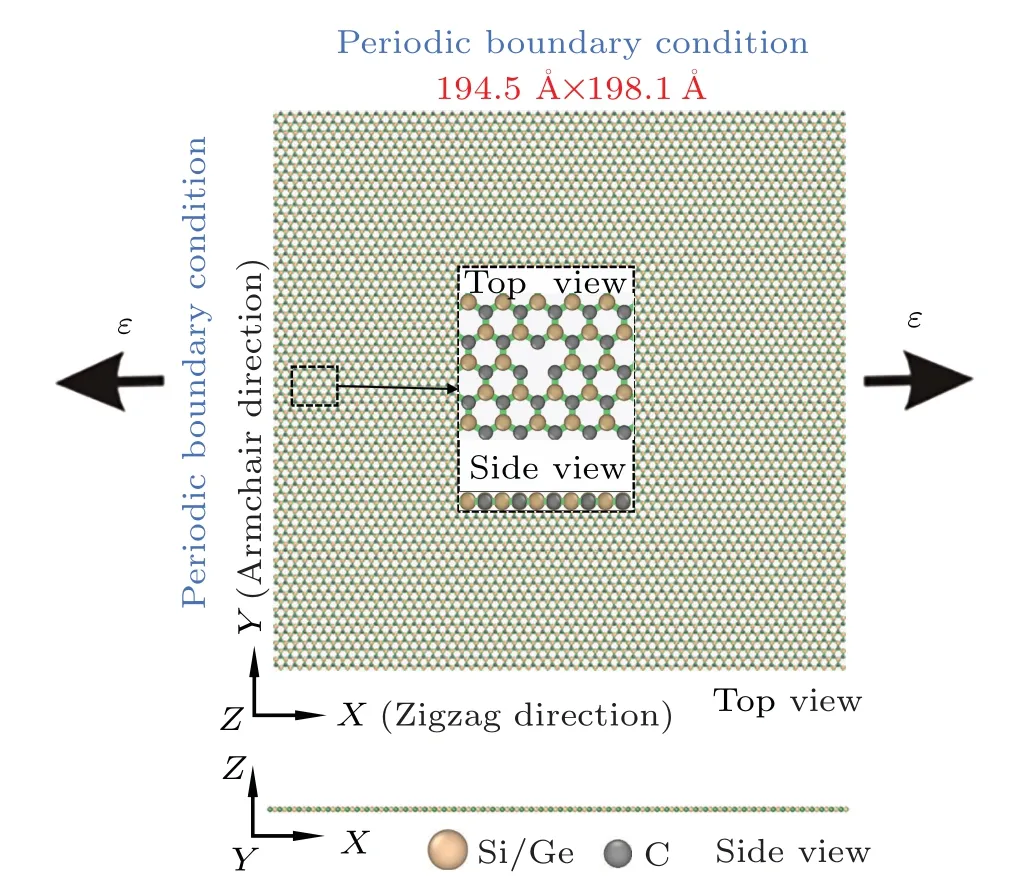
Fig.1.The tensile simulation model of the SiC (or GeC) monolayers with dimensions of 194.5 ˚A×198.1 ˚A.The figure shows the top and side views, and the zoomed-in views (top and side views) of the interface.Both zigzag and armchair directions use periodic boundary conditions.

Non-equilibrium molecular dynamics (NEMD) simulations are used in the thermal simulations to calculate the thermal conductivity with the length and the width of the SiC(or GeC)monolayers at about 200.23 ˚A and 99.09 ˚A,respectively.The studied system was first equilibrated with an NPT ensemble for 100 ps and then the system was relaxed with an NVE ensemble for 2000 ps.The kinetic energy of the hottest atom in the heat sink slab and the coldest atom in the heat source slab are exchanged for 6 ns to produce the heat flux(J).

3.Results and discussion

3.1.Mechanical behavior

Structural integrity is maintained after the total relaxation of the SiC and GeC monolayers,suggesting thermal stability.Next,we investigate the zigzag and armchair direction fracture behaviors of the SiC and GeC monolayers under tensile pressure at 300 K.The obtained deformation and initial crack of the SiC and GeC monolayers are shown in Figs.2(a)and 2(b),where one can see that the atomic stress near the crack has been released, and the fracture strains of SiC and GeC along the zigzag direction are larger than those along the armchair one.Furthermore,the fracture strength of SiC is greater than GeC in both directions, and conversely, the maximal strain that GeC can withstand is greater than SiC in both directions,which is demonstrated by the stress–strain curve of SiC and GeC in Fig.3.

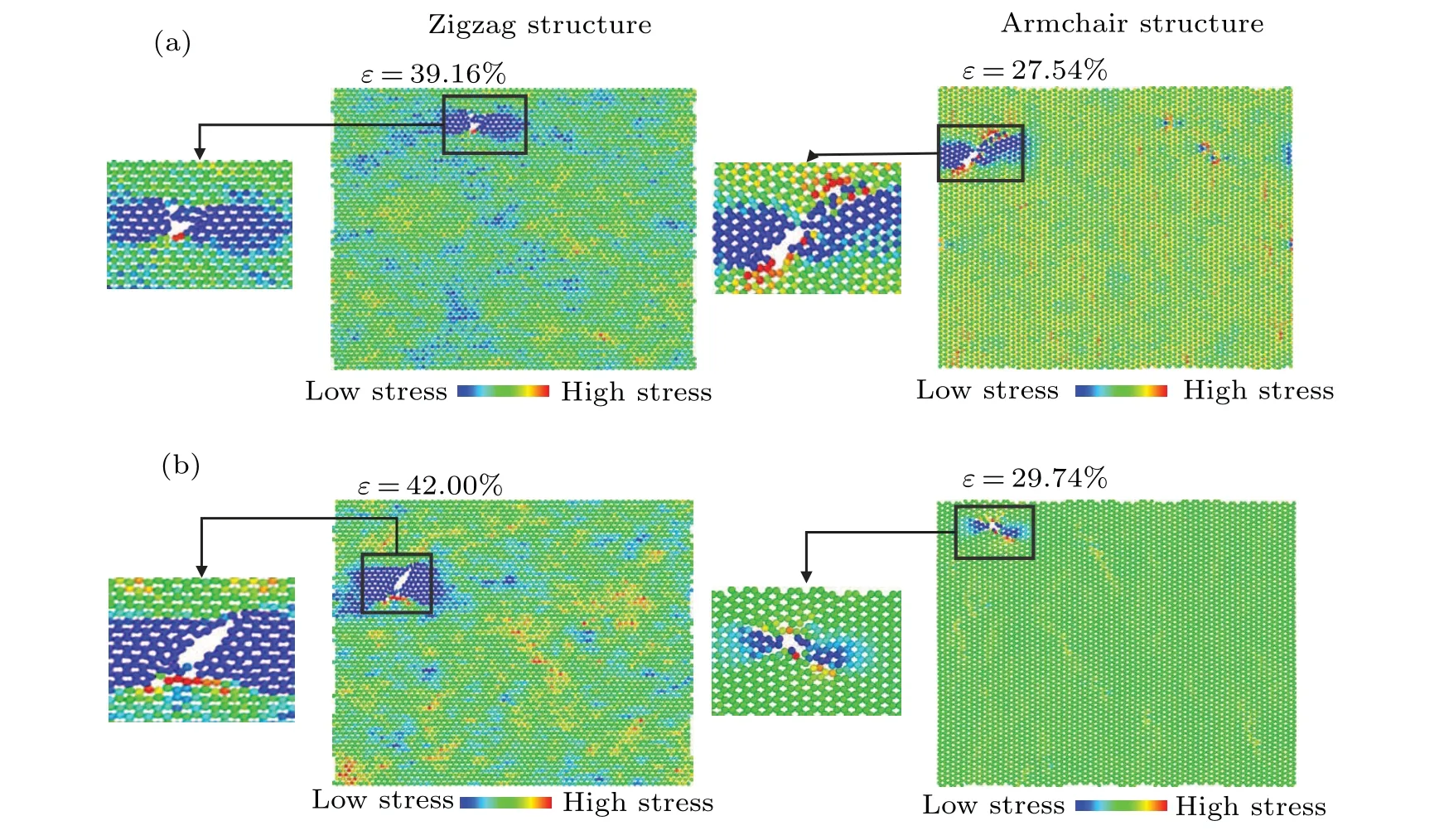
Fig.2.Deformation and initial crack of zigzag and armchair (a) SiC and (b) GeC structures under tensile loading.The color contour in the image shows how the normal stress is distributed along the direction of tensile tension.

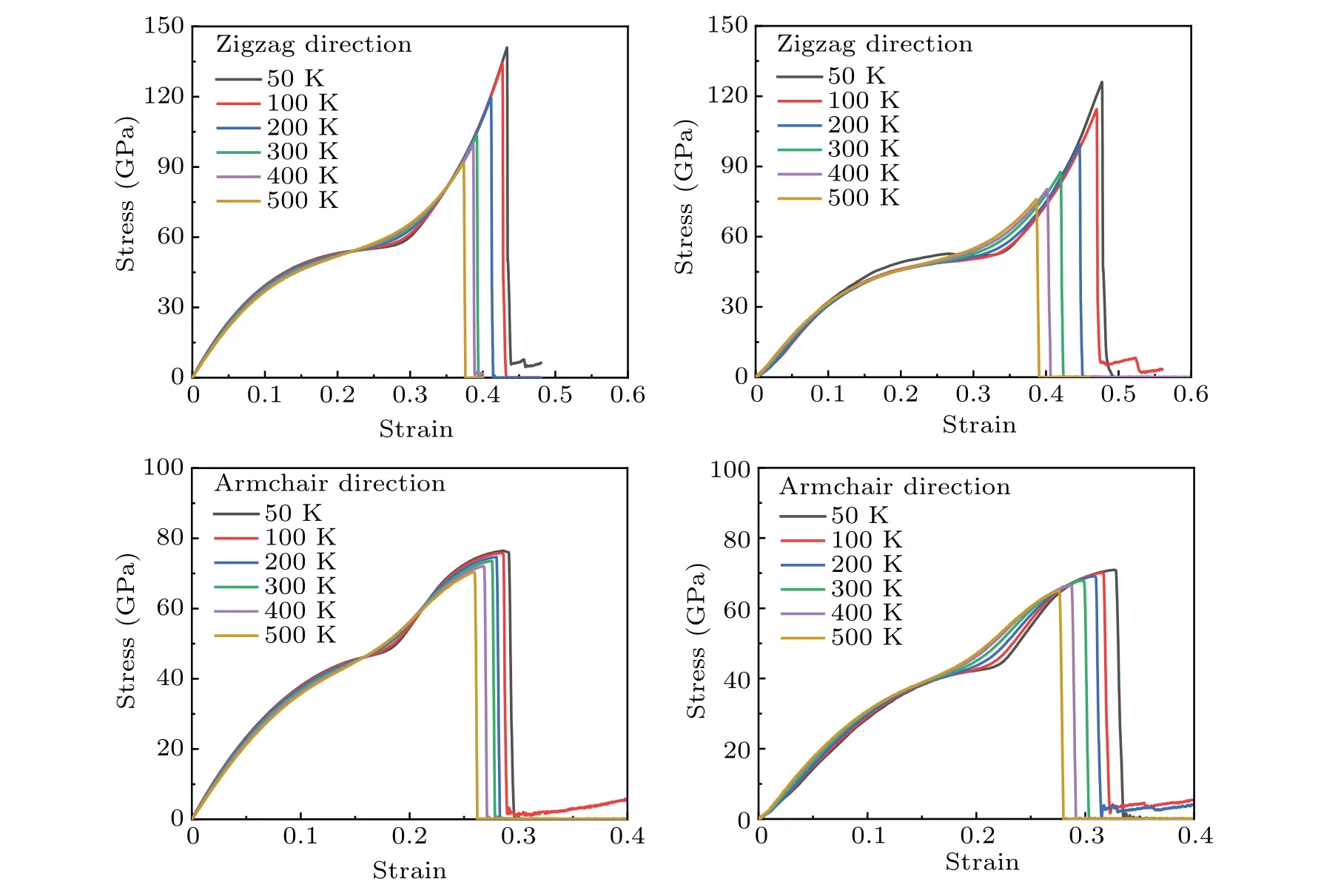
Fig.3.The mechanical characteristics of SiC and GeC structures: the stress–strain curves for SiC(a),(c)and GeC(b),(d)in the zigzag(a),(b)and armchair(c),(d)directions.

In Fig.3, it can be seen that the strain in SiC increases from 0 to 39.16% along the zigzag direction, corresponding to the stress increasing from 0 to 103.55 GPa.At the same time,the strain increasing from 0 to 27.54%can induce stress increases from 0 to 73.59 GPa along the armchair direction.Besides, when an external strain is applied to GeC in the zigzag(armchair)direction of up to 42%(29.74%),the stress increases will increase to 87.64 GPa (67.9 GPa).As shown in the stress–strain curves,both materials exhibit much greater zigzag fracture strengths and strain than armchair fracture strengths and strain, indicating anisotropy in their mechanical properties.The strongest 2D material is graphene,which has a fracture strength of 100–130 GPa and a Young’s modulus of about 1.0 TPa.[34]On comparison, SiC and GeC are much weaker than graphene but far more robust than other 2D materials, such as borophene (23.45–55.9 GPa),[19]silicene(12.5 GPa)[35]and MoS2(11–13 GPa).[17]The effect of temperature on the stress–strain curves of SiC and GeC is also addressed in Fig.3.One can see that SiC and GeC behave mechanically similarly in zigzag (or armchair) directions at various temperatures before fracture, which means that the temperature mainly changes the ultimate fracture performance.

Fig.4.Trends of(a)fracture strength and(b)fracture strain at different temperatures for SiC and GeC.

Then,we investigated the effect of the mechanical characteristics of the SiC and GeC monolayers at different temperatures.The fracture strength and strain of SiC and GeC possess an obvious dependence on the temperature between 50 K and 500 K, as shown in Fig.4.Besides, nonlinear elastic behavior is observed for SiC and GeC.As shown in Fig.4(a), as the temperature rises, both the fracture strength and fracture strain of SiC (or GeC) considerably decline.In more detail,the fracture strength of SiC reduces by 42.5%and 41.59%in zigzag and armchair directions,respectively,when the temperature rises from 50 K to 500 K.The fracture strength of GeC along the zigzag and armchair directions are likewise reduced by around 41.69%and 39.27%, respectively.In addition, the fracture strain of the SiC decreases by 71.2% and 56.9% for zigzag and armchair directions, respectively, while the GeC reduces by about 70.1%and 59.2%along zigzag and armchair directions,respectively.All of these results show that SiC and GeC are more temperature sensitive in terms of their fracture strength in a zigzag direction.At higher temperatures,the vibrations of atoms are greater,and it is easier for local chemical bonds to attain critical bond lengths and break as a result.This phenomenon is known as temperature-induced softening.This resembles the mechanical characteristics of certain common 2D materials,such as MoS2,[36]graphene[34]and silicene,[35]at different temperatures.

Defect engineering is a common technique to modify the characteristics of 2D materials,[6,37,38]and defects also can be introduced easily in SiC and GeC during their fabrication processes.Thus,the response of the mechanical behaviors of SiC and GeC to the initial crack is investigated along zigzag and armchair directions,as shown in Fig.5.We perform MD simulations at 300 K and the obtained fracture strain and fracture strength for various crack lengths (L) in SiC and GeC, ranging up to 5 nm,are shown in Figs.5(a)and 5(b),respectively.Interestingly, SiC and GeC fracture strengths can be significantly reduced by a pre-existing crack in both zigzag and armchair orientations.Evidently,the shorter crack length can tune the fracture strength and strain of the SiC and GeC more effectively.

Fig.5.(a)Schematic of applied stress on SiC(or SiC)with defective structure; the calculated (b) fracture strength and (c) the fracture strain of the SiC and GeC as a function of crack length(L)under tensile loading.

3.2.Thermal properties

The SiC and GeC monolayers possess semiconductor characteristics, suggesting desirable applications in nanoelectronics and thermoelectric devices, therefore, their heat transport properties are also critical.The thermal conductivities of SiC and GeC are discussed using NEMD simulations.As shown in Fig.6(a), both ends of the SiC (or GeC) monolayer are fixed, and hot and cold baths are located near the fixed parts.Thus, the heat flux is along thexdirection.The thermal properties in zigzag and armchair directions are investigated by setting them as thexdirection.The temperature profiles, after reaching a steady state, of SiC and GeC in the zigzag direction are demonstrated in Fig.6(b).For pure SiC and GeC,by fitting the linear area(depicted by a straight line)on the temperature profile,the temperature gradient(dT/dx)is derived.Following that, Fourier’s law is used to compute the thermal conductivity(κ)

whereArepresents the region in cross-section through which the heat flux flows.In order to obtain the thermal conductivity at room temperature (300 K), the hot and cold baths fixed at both ends in Fig.6(a) were set to 320 K and 280 K, respectively.Therefore, the thermal conductivity of pure SiC at a temperature of 300 K is calculated as 16.89 W·m−1·K−1and 18.99 W·m−1·K−1along the zigzag and armchair directions,respectively, which are higher than those of transition metal dichalcogenides materials, such as MoS2(5.93 W·m−1·K−1)and WSe2(7.09 W·m−1·K−1).[19]Additionally,pure GeC has a thermal conductivity of 3.89 W·m−1·K−1in the zigzag direction and 4.49 W·m−1·K−1in the armchair direction.Compared to BCN, which has a thermal conductivity of 28–46 W·m−1·K−1, SiC and GeC exhibit a much lower thermal conductivity.[39]

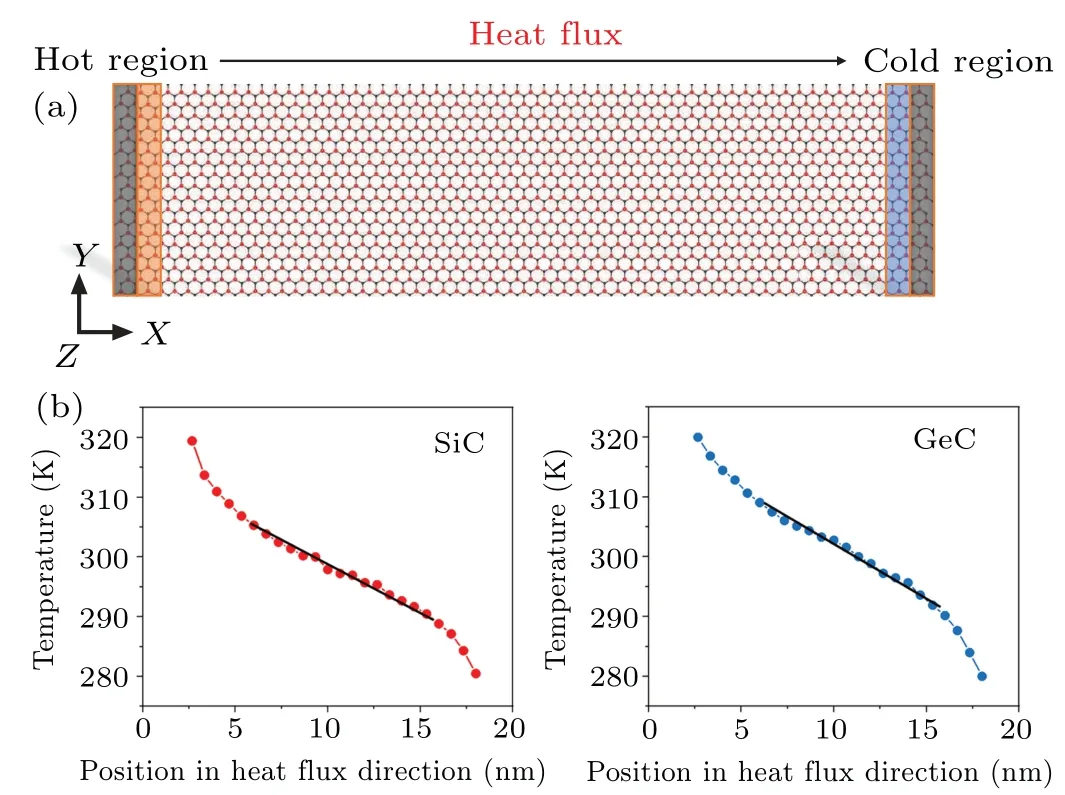
Fig.6.(a) Schematic diagram of the heat transfer model and (b) the calculated temperature profiles of pure SiC and GeC monolayers along the zigzag direction.

Then, to explore the effect of size on the tunable thermal property of SiC and GeC,we fixed the value of the width and changed the length from 200 ˚A to 2000 ˚A at 300 K.The calculated thermal property of SiC and GeC with different lengths is given in Fig.7(a), which shows that the thermal conductivity of SiC sheet increases from 16.89 W·m−1·K−1to 85.67 W·m−1·K−1along the zigzag direction and from 18.99 W·m−1·K−1to 82.79 W·m−1·K−1along the armchair direction.The thermal conductivity of pure GeC sheet is enhanced from 3.89 W·m−1·K−1to 34.37 W·m−1·K−1along the zigzag direction and from 4.49 W·m−1·K−1to 32.74 W·m−1·K−1along the armchair direction.These results indicate an obvious size dependence of the thermal property of SiC and GeC.

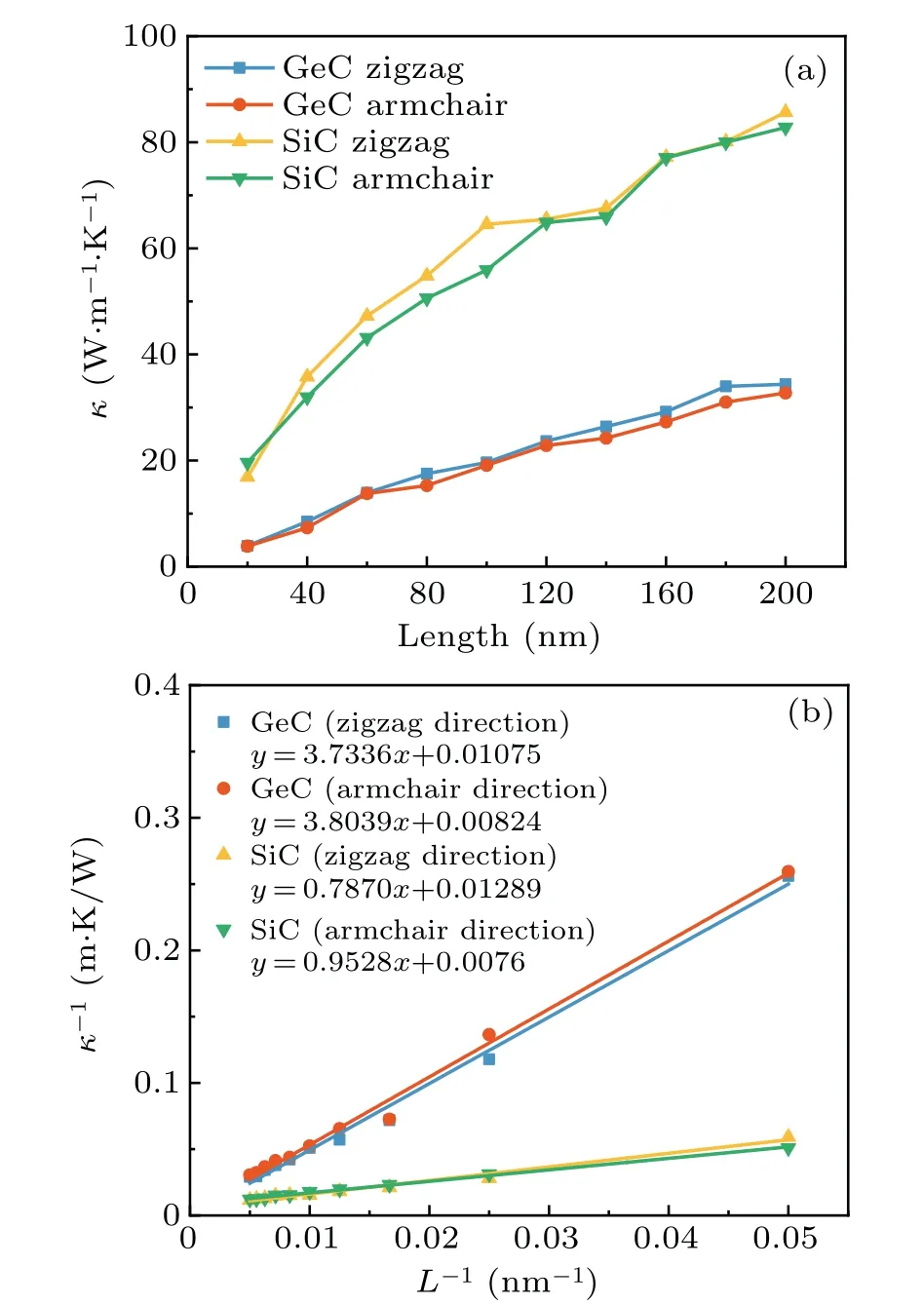
Fig.7.(a) Thermal conductivity measured in pure SiC and GeC at various lengths; (b)the relationships between the inverse thermal conductivity and the inverse sample length for pure SiC and GeC.

When the length of the 2D material is shorter than the phonon mean free path(MFP),which is a common approach to optimizing the heat transport performance of 2D materials,the system size has a significant impact on the thermal conductivity of these materials.[40]The following connection between the inverse thermal conductivity and the inverse sample lengthL−1are used to calculate the effective MFP:[41]

wherelis MFP andκ∞is the thermal conductivity of an infinitely long sample.From the fitting curve shown in Fig.7(b), the obtained effective MFPs for pure SiC and GeC are 109.97 nm and 321.21 nm, respectively.The thermal conductivity of a pure SiC (GeC) infinite-length sample is 126.46 W·m−1·K−1(85.30 W·m−1·K−1).

Besides, we also calculate the thermal property of SiC and GeC at different temperatures ranging from 100 K to 500 K,as shown in Fig.8(a).One can see that the thermal conductivity of both SiC and GeC in the zigzag and the armchair directions are still almost the same, and the simulation results of SiC show that its thermal conductivity decreases from 29.50 W·m−1·K−1to 13.92 W·m−1·K−1along the zigzag direction, and from 28.60 W·m−1·K−1to 15.23 W·m−1·K−1along the armchair direction,indicating a negative temperature dependence.However,the thermal conductivity of GeC shows no significant difference with temperature.The obtained tunable thermal property of SiC and GeC suggests a promising use for thermoelectric applications.

In Fig.8(a), the SiC monolayer shows a strong temperature-dependent thermal conductivity, which is related to phonon anharmonicity.To explore the potential physical mechanism of temperature-dependent thermal conductivity in the SiC monolayer, we calculate the vibrational density of states(VDOS)in the SiC monolayer at 100–500 K from

whereωis the angular frequency andC(t) represents the velocity autocorrelation function.For total VDOS,C(t) =(t)is the velocity of atomjand the symbol〈〉represents the ensemble average.[42]The calculated results are shown as Fig.8(b)with the phonon frequency ranging from 0 to 40 THz.The peak frequency for the SiC monolayer at 300 K is around 11.5 THz.The peak value of VDOS near 25–40 THz varies significantly with temperature,thus, we focus on this range.As shown in Fig.8(b), the increased temperature causes a significant redshift in the high frequency peaks of SiC, induced by an enhanced phonon anharmonicity, reducing the thermal conductivity and therefore exhibiting a temperature dependence.This phenomenon has also been explored in Janus MoSSe and WSSe monolayers.[43]Our simulations are an important reference for the future development of thermal devices and thermoelectric energy conversion.

4.Conclusion and perspectives

In this study,molecular dynamics simulations were used to systematically examine the in-plane mechanical and thermal transport characteristics of pure SiC and GeC.Both SiC and GeC demonstrate an excellent toughness with fracture strain of about 0.43 and 0.47 in the zigzag direction at 300 K, respectively, which can be decreased by temperature and the introduced crackle.Furthermore, the thermal conductivities of pure SiC (GeC) are calculated as 16.89 W·m−1·K−1(3.89 W·m−1·K−1)and 18.99 W·m−1·K−1(4.49 W·m−1·K−1) along zigzag and armchair directions, respectively,by a non-equilibrium molecular dynamics method.Additionally,the thermal conductivity of SiC(GeC)can reach 85.67 W·m−1·K−1(34.37 W·m−1·K−1) due to a size effect,although an increase in temperature will reduce that.The obtained size and temperature-tunable mechanical and thermal characteristics of SiC and GeC suggest promising applications as thermoelectric and flexible nanodevices.

Acknowledgements

All the authors would like to thank the support of the Natural Science Foundation of Jiangsu(Grant No.BK20220407),the National Natural Science Foundation of China (Grant Nos.12102323, 11890674), the China Postdoctoral Science Foundation (Grant No.2021M692574), and the Fundamental Research Funds for the Central Universities (Grant No.sxzy012022024).This work is also supported by the HPC Center,Nanjing Forestry University,China.