Study of the natural vibration characteristics of water motion in the moon pool by the semi-analytical method*
Li-qin Liu (刘利琴), Yan Li (李妍), Lei Huang (黄磊), You-gang Tang (唐友刚)
State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China, E-mail: liuliqin@tju.edu.cn
(Received May 4, 2015, Revised March 23, 2016)
Study of the natural vibration characteristics of water motion in the moon pool by the semi-analytical method*
Li-qin Liu (刘利琴), Yan Li (李妍), Lei Huang (黄磊), You-gang Tang (唐友刚)
State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China, E-mail: liuliqin@tju.edu.cn
(Received May 4, 2015, Revised March 23, 2016)
The three-dimensional natural vibration characteristics of water inside a moon pool of an ocean structures are studied. The governing equations are derived based on the linear potential flow theory, and the boundary condition of the total opening bottom suggested by Molin is adopted. A semi-analytical method is used to solve the governing equations, and the natural frequencies and the motion modes are obtained. Two types of motions are studied: (1) the piston motion in the vertical direction, and (2) the sloshing motion of the free surface. The influences of moon pool’s structural parameters on the natural frequencies, and the modal shapes are analyzed.
Moon pool, natural vibration characteristics, semi-analytical method, parameter influences
Introduction
The moon pool is an important structure used in the offshore floating structures, such as drilling unit, floating production storage and offloading (FPSO), and Spar platform[1,2]. It goes vertically down through the main structure. The risers and the other important drilling equipment are located in the moon pool to prevent excessive wave and current excitations[3-5]. There are two kinds of natural vibration modes of water in the moon pool: (1) the piston-like motion along the depth direction of the moon pool, and (2) the sloshing motion caused by the free liquid surface[6-8].
The natural vibration characteristics of water in a moon pool were extensively studies, to predict the coupled motion of the moon pool and the offshore structure in the complicated ocean environment. Based on a series of model tests, Aalbers[9]developed the relativemotion equations of water in a ship’s moon pool. The results show that the natural vibration characteristics of water in the moon pool depend on parameters, such as the depth of the water column, the heave amplitude, and the diameter of the moon pool. By applying a fictitious boundary condition at the bottom of a moon pool, Molin[10]studied the natural frequencies and the modal shapes of both the piston mode and the sloshing mode of water in the moon pool and obtained approximate expressions of natural frequencies. Sphaier et al.[11]carried out the model tests of a mono-column platform with a semi-closed moon pool, the results show that the motion of the water column is smaller for smaller moon pool opening. Hence, the moon pool can be used as an effective device to reduce the vertical motion of a mono-column platform. Faltinsen et al.[12]studied the two-dimensional piston-like motions of the water inside a moon pool with a vertical harmonic motion by the domain-decomposition method. The model experiments were carried out to compare with the analytical results. By applying Newton’s second law, Gupta et al.[13]developed a 2-DOF (degree of freedom) coupled motion equations for the heave of a Spar platform and the vertical oscillation of the water column inside a moon pool. Using the CFD method, Kristiansen and Faltinsen[14,15]investigated the influence of the nonlinear free surface, the damping of the boundary layersand the flow separation on the piston motion of water in a moon pool. It is found that the flow separation is the main cause of the discrepancies between the measured results and those estimated by the linear theory. Tonje[16]studied the influence of the water inside a moon pool on the installation of the cargo oil pump. The results show that in the resonance region, the amplitude of the water movement inside the moon pool is greater than that outside the moon pool. Based on the Navier-Stokes equations and the volume of fluid (VOF) method, Sun et al.[17]developed a 3-DOF numerical wave tank. The interaction between the hull and the water motion inside a moon pool was also analyzed. Liu et al.[18,19]studied the influence of the water motion inside a moon pool on the heave motion of a Spar platform. The model experimental results were used to verify the analytical results.
The present work studies the three-dimensional natural vibration characteristics of water inside a moon pool, as well as the influences of moon pool’s dimensional parameters on the natural frequencies and the modal shapes of the water motion inside the moon pool. Using the Galerkin method, the semi-analytical solution is obtained.
1. Solution of governing equations of water in moon pool
1.1Governing equations
The Cartesian coordinates and a schematic diagram of a three-dimensional moon pool are shown in Fig.1, wherel,bandhrepresent the length, the width and the water depth of the moon pool, respectively. The main structure is assumed to be motionless, since its scale is much larger than that of the moon pool. Therefore, it is assumed the length and the width of the main structure are infinite. The values ofl,bandhare mainly based on the parameters of the drilling units given in the following sections.

Fig.1 Coordinates of the three-dimensional moon pool
Assuming that the flow is incompressible, inviscid, irrotational, and the motion of water inside the moon pool can be described by the boundary value problem of Laplace’s equation. At the free surface, the velocity potential function can be expressed in terms of time and space, as follows
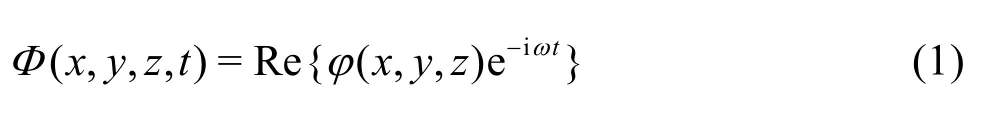
whereΦ(x,y,z,t)is the velocity potential function,ωis the natural frequency of the liquid motion in the moon pool,ϕ(x,y,z)is the velocity potential function in space. According to the potential flow theory, the governing equation of the water motion in a moon pool is
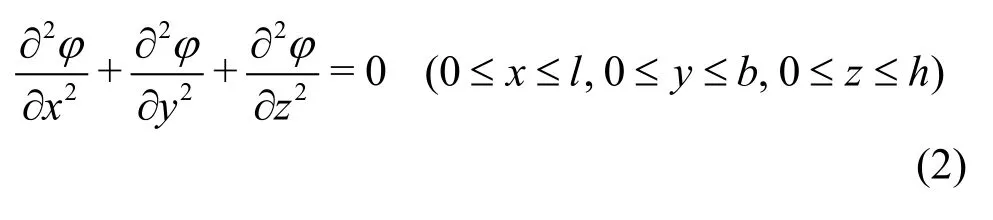
For a moon pool with impermeable vertical walls, the boundary conditions are

The linear free surface condition is expressed as

By taking the fictitious bottom as the boundary condition proposed by Molin[10], the influence of the outlet at the bottom of the moon pool can be described by the following formula
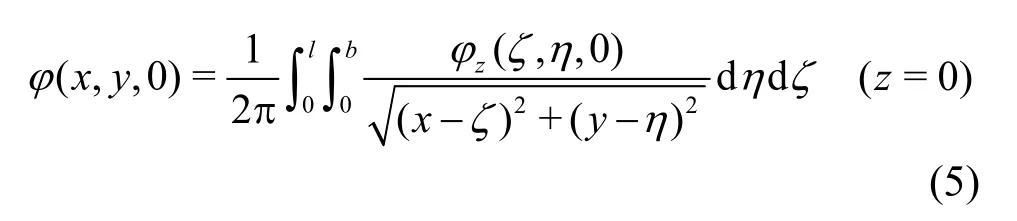
1.2Semi-analytical solution
Equations (1)-(4) are solved using the method of separation of variables. Assuming that the fluid velocity potentialϕcan be written as

Substituting Eq.(6) into Eq.(1), a series of ordinary differential equations are obtained, as follows:
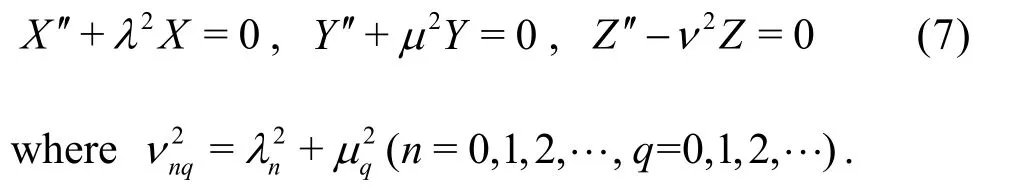
The general solutions of Eq.(7) can be written as

With the boundary condition as described by Eq.(3) and the condition of the nontrivial solutions, one obtains

The general solution ofϕ(x,y,z)can be written as



Substituting Eq.(14) into the bottom boundary condition Eq.(5), one obtains

The Galerkin method is then used to integrate Eq.(15). Integrating the left and right sides of Eq.(15) with respect toxandy, respectively, and settingν00=1/h, one obtains

Multiplying both sides of Eq.(15) with cosλmx⋅cosμpy, and integrating the left and right sides of the resultant equation with respect toxandy, respectively, we have


Fig.2 Comparison of the integration values
Eqs.(16) and (17) can then be rewritten as


Table 1 Integration results oftmnpq
whereκ=1/2πbl. Substituting Eq.(14) into the free surface condition Eq.(4), one obtains
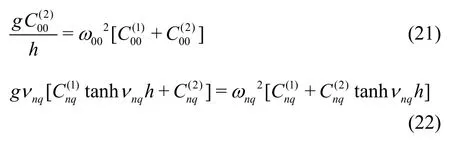
whereωijis the natural frequency of each mode, whereiandjdenote the model orders in length and width directions, respectively. Rewrite Eqs.(21) and (22) into the matrix form, as follows:


Solving Eq.(23) for the eigenvector matrixesC(2), and substitutingC(2)into Eq.(24), we obtain an expression forC(1). SubstitutingC(1)andC(2)into Eq.(14), and solving it for the fluid velocity potentialϕ, the wave elevationζcan be obtained in the following form

With Eq.(25), the shape of the free surface will be used to discuss the vibration characteristics of the water inside a moon pool in Section 3.
2. Numerical results and analyses
The coefficient matrixtmnpqis calculated numerically by using the Simpson’s method. Calculatingtmnpqis the most important step in the total process. For the two-dimensional coefficient matrixtmn, the dimensionless results calculated in this paper are compared with those of Molin’s[10], as shown in Fig.2. Good agreement can be seen.
Table 1 shows part of the integration results. It is seen that when both the sum ofmandn, and that ofpandqare even numbers, the integration result is nonzero. Substituting the integration results into Eq.(23), we obtain the matrixC(2)and the natural frequencyωijfor each mode, whereiandj, respectively, denote the model order in the length and width directions of the moon pool. The coefficient matrixC(1)is then determined by solving Eq.(24). The matricesC(1)andC(2)are diagonally dominated, and the velocity potentialϕof each mode is dominated by the main diagonal elements ofC(1)andC(2).
2.1Comparing semi-analytical results with CFD results
To verify the validity of the semi-analytical results, the CFD method is used. To save the calculation time, as shown in Fig.3, a two-dimensional CFD model is developed. In the model, the width of the moon pool,b, is 20 m, the tank’s width is 160 m and the water depth takes values of 2 m and 10 m in the simulation.

Fig.3 (Color online) CFD model
Moving the moon pool structure in the vertical direction with a period of 2π/ω0, whereω0is the piston natural period of the water motion in the moon pool, the piston resonance of the water in the moon pool is expected to be excited. Figure 4 shows the comparisons of the free surface calculated by the semianalytical and the CFD methods forh=2 mandh=10 m, where S-A denotes the results calculated by the semi-analytical method. It is apparent that for the piston mode, the free surfaces estimated by the semianalytical method generally agree well with those estimated by the CFD method. There are small differences at the center and at the two boundaries of the moon pool. This is because in the CFD method, the viscosity is included, while in the semi-analytical method, it is not.

Fig.4 Comparisons of free surface elevation results from semianalytical and CFD methods for the piston mode

Fig.5 Semi-analytical results vs. CFD results for the first order sloshing mode
Moving the moon pool structure in the horizontal direction with a period of 2π/ω1, whereω1is the first order sloshing natural frequency of water in the moon pool, the first order sloshing resonance of the water in the moon pool is expected to be excited. Figure 5 shows the comparisons of the first order sloshing mode calculated by the semi-analytical and theCFD methods forh=2 mandh=10 m. It is apparent that for the first order sloshing mode, the free surfaces estimated by the semi-analytical method generally agree well with those estimated by the CFD method.
2.2Natural frequencies
The water inside a moon pool has two forms of motion, the piston mode and the sloshing mode, in the length and the width directions.ϕ00is defined as the spatial velocity potential function of the piston mode, which only depends on the variablez, as expressed in Eq.(13). Whileϕnq(nandqcannot be both zero at the same time) relates tox,yandz, as expressed in Eq.(12), and is defined as the sloshing modes. According to the work of Monlin[10], the sloshing modes can be categorized as follows:
(1) Withm,n,pandqall being even numbers, it is the full symmetric mode. In this mode, the modal shape is symmetrical in both width and the length directions.
(2) Withmandnbeing odd numbers, andpandqbeing even numbers, it is the longitudinal asymmetric mode. In this mode, the modal shape is symmetrical in the width direction but asymmetrical in the length direction.
(3) Withmandnbeing even numbers, andpandqbeing odd numbers, it is the transverse asymmetric mode. In this mode, the modal shape is asymmetrical in the width direction but symmetrical in the length direction.
(4) Withm,n,pandqall being odd numbers, it is the full asymmetric mode. In this mode, the modal shape is asymmetrical in both width and length directions.
Further, Tables 2 and 3 show some natural frequencies of water motions inside a moon pool of a square cross section and a rectangle cross section, respectively.
The influences of moon pool’s parameters, such as the lengthl, the widthband the depth of water in the moon poolh, on the natural frequencies of the piston mode and the first three orders of sloshing modes are analyzed. The results are shown in Figs.6-9.

Table 3 Natural frequencies (l=20 m,b=10 m,h=10 m)
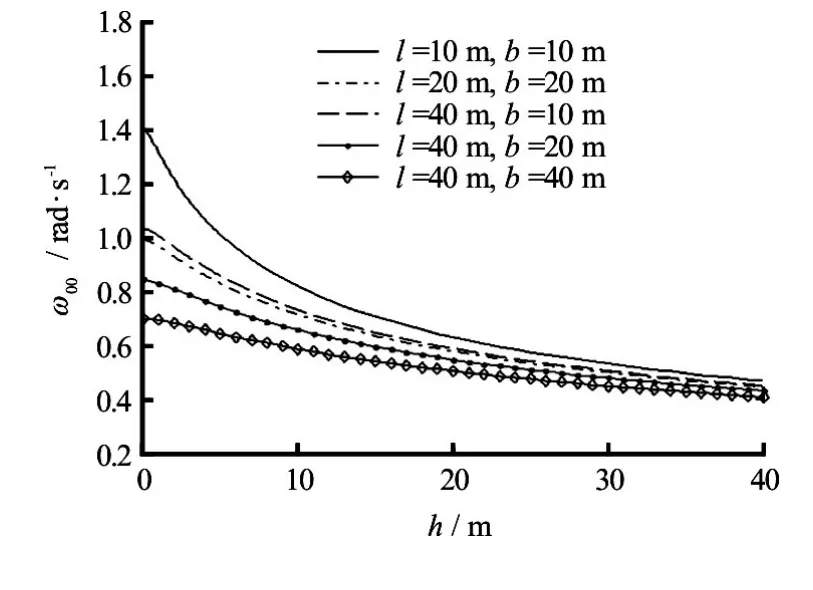
Fig.6 Effect of moon pool’s parameters onω00

Fig.7 Effect of moon pool’s parameters onω22
Figure 6 shows the influences of moon pool’s parameters on the natural frequencies of the piston mode. It is apparent thatω00decreases with the increase of the lengthland the widthb. Forh=10 m andl=40 m,ω00is 0.74 rad/s (corresponding to the natural period of 8.49 s), 0.68 rad/s (corresponding to the natural period of 9.24 s) and 0.58 rad/s (corresponding to the natural period of 10.83 s) forb=10 m, 20 m and 40 m, respectively. Forb=10 mandh= 10 m, iflincreases from 10 m to 40 m,ω00decreases from 0.82 rad/s (corresponding to the natural period of 7.66 s) to 0.72 rad/s (corresponding to thenatural period of 8.72 s).ω00decreases with the increase ofh.The influences oflandbonω00become indistinct for highh.With the increase ofl,bandh,the natural frequency of the piston mode of water in the moon pool approaches the characteristic wave frequency of the rough sea. As such, the large amplitude piston motion of water in the moon pool may be excited. In the design of the moon pool, appropriate values ofl,bandhshould be used so as to avoid the large amplitude piston motion of water in the moon pool and to reduce the influence of moon pool’s water motion on the motion of the floating body.
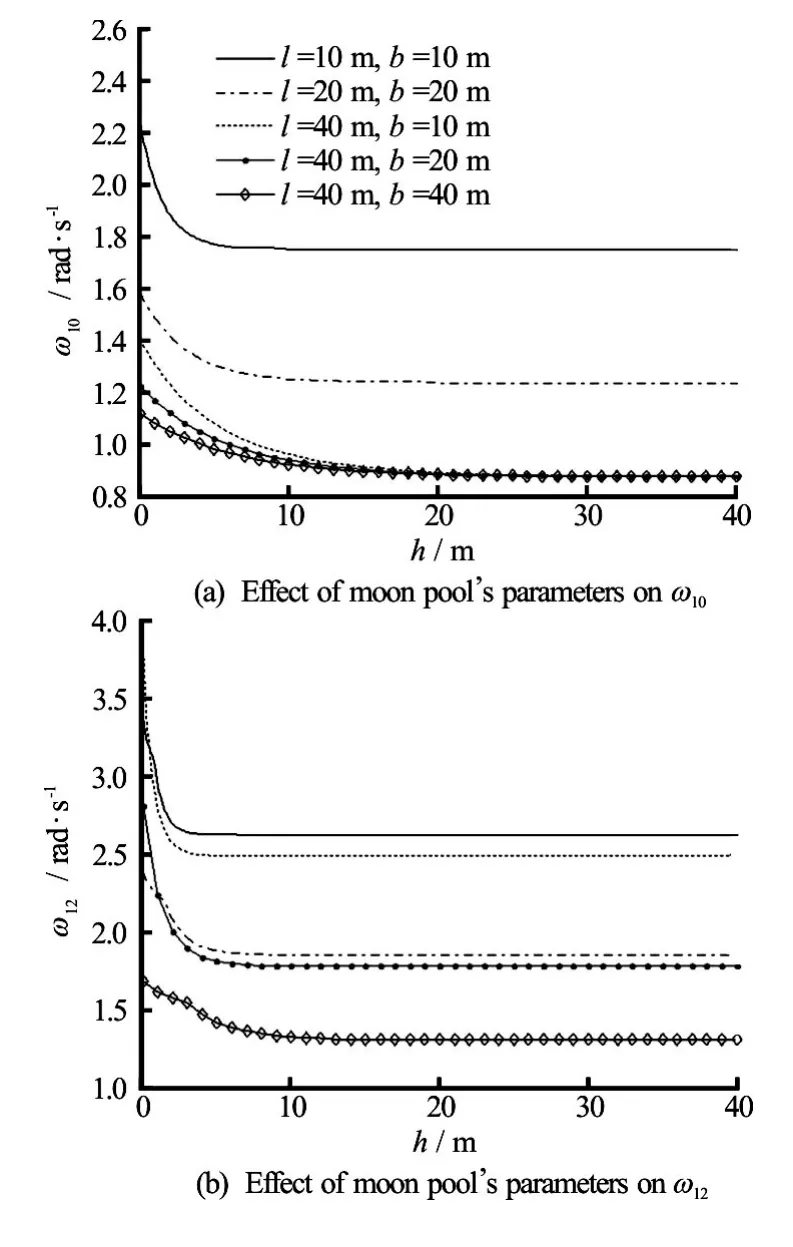
Fig.8 Effects of moon pool’s parameters on the natural frequencies of the longitudinal asymmetric modes
Figures 7-9 show the influences of the moon pool’s parameters on the natural frequencies of the sloshing modes. It can be seen that the natural frequencies of the sloshing modes are higher than that of the piston mode. Figure 7 shows thatω22decreases slightly with the increase ofhforh≤3m. It mainly depends on the lengthland the widthbof the moon pool forh>3m. Figure 8 shows the influences of moon pool’s parameters on the natural frequenciesω10andω12of the longitudinal asymmetric modes. Figure 9 shows the influences of moon pool’s parameters on the natural frequenciesω11andω13of the full asymmetric modes. As shown in Figs.8 and 9, it is apparent that whenhis small, the natural frequencies decrease with the increase ofh. However, whenhis large enough, the natural frequencies of the sloshing modes mainly depends on the lengthland the widthbof the moon pool.

Fig.9 Effects of moon pool’s parameters on the natural frequencies of the full asymmetric modes
2.3Modal shapes
By using Eq.(25), the modal shapes of the piston mode and some sloshing modes are analyzed. For the piston mode, the free surface oscillates up and down with respect to the equilibrium position. The sloshing modes are classified into four types: (1) fully symmetric mode, (2) longitudinal asymmetric mode, (3) transverse asymmetric mode, and (4) fully asymmetric mode. The influences of moon pool’s parameters, including the lengthl, the widthb, and the heighthof water in the moon pool on the modal shapes are analyzed in this section. The results are shown in Figs.10-17.
Figure 10 shows the shapes of the piston mode ofω00for different moon pool’s parameters. It is apparent that the depth of water in the moon pool influences the modal shape significantly. Forh=1m, as shown in Fig.10(a), the modal shape of the piston mode has a peak in the center of the moon pool. The peak value decreas es with the i ncrea se ofh.F orh=5 m, as showninFig.10(b),thepeakvalueisverysmall.Fig.10(d) shows that the shape of the piston mode is symmetrical both inxandydirections.
As shown in Fig.11, for a moon pool of rectangular cross-section, the modal shapes ofω02andω20are fully symmetrical. Figure 12 shows the second sloshing mode of water in the moon pool. It can be seen that the modal shape ofω22is symmetrical in bothxandydirections.

Fig.10 (Color online) Shapes of piston mode ofω00

Fig.11 (Color online) Shapes of fully symmetric mode ofω02andω20(l=20 m,b=10 m,h=1m)

Fig.12 (Color online) Shapes of fully symmetric modes ofω22(l=20 m,b=10 m,h=1m)
Figures 13 and 14 show the influences of moon pool parameters on the modal shape ofω10. It is appa-rent that the modal shape ofω10is asymmetrical inxdirection and symmetrical inydirection. For the largerh, the curve of the two-dimensional mode along the longitudinal direction of the moon pool is close to that of the trigonometric function. As such, the function can be determined by the analytical method similar to that for the problem of liquid tank sloshing[20]. With the decrease ofh, as shown in Fig.14(a), the curve becomes irregular near the boundaries ofx= 0 m andx=80 m, which cannot be determined analytically. Figure 14(b) shows the amplitude of the twodimensional modal curve along the transverse direction of the moon pool, which decreases with the increase ofh.

Fig.13 (Color online) Shapes of longitudinal asymmetric modes ofω10(l=80 m,b=20 m,h=1m)
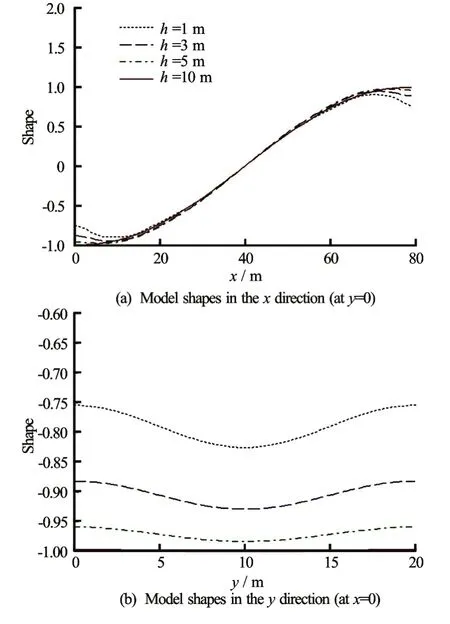
Fig.14 Two-dimensional modal shapes ofω10for differenth(l=80 m,b=20 m)

Fig.15 (Color online) Shapes of longitudinal asymmetric modes ofω12andω30(l=80 m,b=20 m,h=1m)

Fig.16 (Color online) Shapes of transverse asymmetric modes ofω01andω21(l=20 m,b=20 m,h=1m)
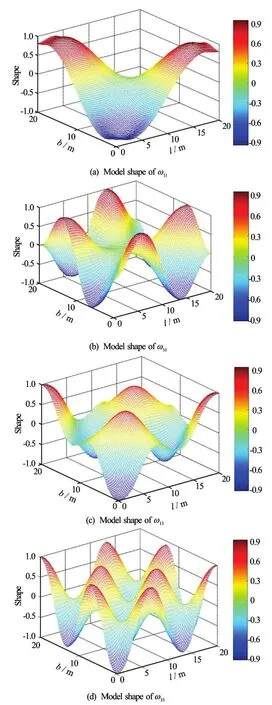
Fig.17 (Color online) Shapes of fully symmetric modes ofω11,ω31,ω13andω33(l=20 m,b=20 m,h=1m)
Figure 15 shows the shapes of the longitudinal asymmetric modes ofω12andω30forl=80 m,b=20 mandh=1m. Figure 16 shows the shapes of the transverse asymmetric modes ofω01andω21. Figure 17 shows the shapes of fully asymmetric modes ofω11,ω31,ω13andω33.
3.Conclusions
Using the semi-analytical method, the natural vibration characteristics of water inside a moon pool are studied. The influences of moon pool’s dimensional parameters on the natural frequencies and the modal shapes are also investigated. The modal shapes of the sloshing motion are presented and the influence of moon pool’s structural parameters is analyzed. The conclusions are as follows:
(1) The natural frequency of the piston mode of water in the moon pool approaches the characteristic wave frequency of the rough sea with the increase ofl,bandh. As such, the large amplitude piston motion of water in the moon pool may be excited in the rough sea. In the design of the moon pool, appropriate values ofl,bandhshould be used so as to avoid the large amplitude piston motion of water in the moon pool.
(2) The shape of the piston mode is symmetrical both inxandydirections. The depthhinfluences the modal shape significantly. The piston mode has a noticeable peak in the center of the moon pool for smallh,and the peak value decreases with the increase ofh.
(3) The natural frequencies of the sloshing modes are higher than that of the piston mode. Whenhis small the natural frequencies of the sloshing modes decrease with the increase ofh. However, whenhis high the natural frequencies of the sloshing modes mainly depend on the lengthland the widthbof the moon pool.
[1]FaltinsenO. M. Hydrodynamics of marine and offshore structures [J].Journal of Hydrodynamics, 2015, 26(6): 835-847.
[2] Zhang H. S., Zhou H. W.Wave radiation and diffraction by a two-dimensional floating body with an opening near a side wall[J].China Ocean Engineering, 2013, 27(4): 437-450.
[3] Dong Y. Q. Wave loads and response of the oil-extraction platform in deep ocean [M]. Tianjin, China: Tianjin University Press, 2005(in Chinese).
[4] Drobyshevski Y. Hydrodynamic coefficients of a twodimensional, truncated rectangular floating structure in shallow water [J].Ocean Engineering, 2004, 31(3-4): 305-341.
[5] Wei Y., Yang J. and Chen G. et al. Experimental study on the hydrodynamic performance of FDPSO and SRV [J].Ships Offshore Structure, 2012, 7(4): 1-13.
[6] Faltinsen O. M., Timokha A. Sloshing [M]. Cambridge,UK: Cambridge University Press, 2009.
[7] Yang S. H., Lee S. B., Park J. H. et al.Experimental study on piston-and sloshing-mode moonpool resonances[J].Journal of Marine Science and Technology, 2016, 21(4): 715-728.
[8] Servan C. B., Cercos Pita J. L., Colom Cobb J.Time domain simulation of coupled sloshing-seakeeping problems by SPH-FEM coupling[J].Ocean Engineering, 2016, 123: 383-396.
[9] Aalbers A. The water motions in a moon pool [J].Ocean Engineering, 1984, 11(6): 557-579.
[10] Molin B. On the piston and sloshing modes in moon pools [J].Journal of Fluid Mechanics, 2001, 430: 27-50.
[11] Sphaier S., Torres F., Masetti I. et al. Mono-column behavior in waves: Experimental analysis [J].Ocean Engineering, 2007, 34(11-12): 1724-1733.
[12] Faltinsen O. M., Rognebakke O. F., Timokha A. N. Twodimensional resonant piston-like sloshing in a moon pool [J].Journal of Fluid Mechanics, 2007, 575: 359-397.
[13] Gupta H., Blevins R., Banon H. Effect of moon pool hydrodynamics on Spar heave [C].Proceedings of the ASME 2008 27th International Conference on Ocean, Offshore and Arctic Engineering. New York, USA: American Society of Mechanical Engineers, 2008, 275-282.
[14] Kristiansen T., Faltinsen O. M. A two-dimensional numerical and experimental study of resonant coupled ship and piston-mode motion [J].Applied Ocean Research, 2010, 32(2): 158-176.
[15] Kristiansen T., Faltinsen O. M. Gap resonance analyzed by a new domain-decomposition method combining potential and viscous flow DRAFT [J].Applied Ocean Research, 2012, 34(1): 198-208.
[16] Tonje C. S. Assessment of critical factors when running and relieving Framo pump modules through moon pool [D]. Master Thesis, Stavanger, Norway: Norway University of Stavanger, 2011.
[17]Sun C. W., Yang J. M., Lv H. N. Numerical investigation on motions of vessel with moon pool in wave conditions [J].The Ocean Engineering, 2013, 31(4): 21-29(in Chinese).
[18]Liu L., Incecik A., Zhang Y. Analysis of heave motions of a truss spar platform with semi-closed moon pool [J].Ocean Engineering, 2014, 92: 162-174.
[19] Liu L., Qiu Y., Li Y.Effects of water inside semiclosed moon pool on the hydrodynamic coefficients and heaving damping of a truss spar platform[J].Journal of Offshore Mechanics and Arctic Engineering, 2016, 138(4): 041302.
[20] Ibrahim Raouf A. Liquid sloshing dynamics theory and application [M]. Cambridge, UK: Cambridge University Press, 2005.
* Project supported by the Natural Science Foundation of China (Grant No. 51179125), the Greative Research Groups of the Natural Science Foundation of China (Grant No. 51621092) and the Natural Science Foundation of Tianjin (Grant No. 16JCYBJC21200).
Biography:Li-qin Liu (1977-), Female, Ph. D., Associate Professor
- 水动力学研究与进展 B辑的其它文章
- Journal of Hydrodynamics, Vol. 28 Annual Classified Catalog (2016)
- Numerical study of the flow and dilution behaviors of round buoyant jet in counterflow*
- Numerical simulation of flow through circular array of cylinders using porous media approach with non-constant local inertial resistance coefficient*
- Numerical estimation of bank-propeller-hull interaction effect on ship manoeuvring using CFD method*
- Insoluble additives for enhancing a blood-like liquid flow in micro-channels*
- Entropy generation analysis for the peristaltic flow of Cu-water nanofluid in a tube with viscous dissipation*

