Interaction solutions and localized waves to the(2+1)-dimensional Hirota–Satsuma–Ito equation with variable coefficient
Xinying Yan(闫鑫颖), Jinzhou Liu(刘锦洲), and Xiangpeng Xin(辛祥鹏)
School of Mathematical Sciences,Liaocheng University,Liaocheng 252059,China
Keywords: (2+1)-dimensional variable coefficient Hirota–Satsuma–Ito equation,Hirota bilinear method,long wave limit method,N-soliton solutions
1.Introduction
Research of solutions to non-linear evolution equations(NLEEs) plays an important role in the field of nonlinearity.Therefore, search for efficient solution methods has gained more and more attention.To date, there are several effective methods that have been commonly used by mathematicians, such as Darboux transformation,[1,2]B¨acklund transformation,[3–5]Lie group method,[6–9]inverse scattering method,[10]Hirota bilinear method,[11–14]and hyperbolic method.[15]Among them,the Hirota bilinear method proposed by Hirota is a straightforward method for finding exact solutions of NLEEs.The general idea of the bilinear method is to transform the equation into a bilinear form based on the derivative operator defined by Hirota, and to solve the equation in the bilinear form by appropriately dependent variable transformation.The key to the bilinear approach is to find the appropriately dependent variable transformation.There are many kinds of solutions that can be obtained by solving NLEEs in different ways, such as soliton solutions, breather wave solutions, lump solutions, periodic solutions, trigonometric solutions, and interaction of different solutions.[16–19]Among them,soliton solutions are one of the most important research topics.N-soliton solutions are exact multiple wave solutions of the integrable equations and are important for describing nonlinearities in areas such as shallow water waves,plasma,and nonlinear optics.[20–22]However,in recent years,existence of interaction solutions of two different solutions of the integrable equation has attracted much attention.This is because many phenomena occurring in nature can be more easily explained by interaction solutions.[23,24]Thus,there are more and more researchers to study the interaction solutions deeply.For example, Yuanet al.constructed various localized interaction solutions including the general M-lumps, Tbreathers and hybrid wave solutions.[25]These solutions play important roles in solving practical problems.
The (2+1)-dimensional Hirota–Satsuma–Ito (HSI) equation is an integrable equation.It is obtained by the Hirota–Satsuma (HS) equation with some transformations.[26]The form of the HS equation is
With the transformationu= 2(lnf)xx, the form of the HSI equation is
whereu,v, andωare the functions ofx,y,t.Hence, we can get the following form after some calculations:
In Ref.[27], Liuet al.analyzed the HSI equation with constant coefficient using the Hirota bilinear method and obtained some interactions of different types of solutions.Kumaret al.[28]studied the HSI equation by Lie symmetry analysis and obtained multiple soliton solutions and interactions of soliton solutions.
Equations with variable coefficients can explain more natural phenomena than equations with constant coefficients.Therefore,in this article we study the HSI equation with variable coefficient(vcHSI).Without loss of generality,the vcHSI can be assumed as follows:
wherea(t),c(t),d(t), ande(t) are free functions about timet.It is obvious that Eq.(4) reduces to Eq.(3) whena(t)=c(t)=d(t)=e(t)=1.However, the integrability of Eq.(4)is uncertain.The Painlev´e analysis method is an effective way of judging the integrability of nonlinear differential equations and finding exact solutions.[29,30]We now perform the Painlev´e analysis on Eq.(4) to find integrability conditions.The solution of Eq.(4)can be assumed as follows:
whereujandϕare functions aboutx,y,t.
Substitutingu=u0ϕ−αinto Eq.(4)yieldsα=1 by homogeneous balance.Hence,u=u0/ϕwhenj=0.After some calculations,we can reach
Substitutingα=1 into Eq.(5)yields
The resonance points can be determined atj=−1,1,4,6 after substituting Eq.(6)into Eq.(4)and extracting the coefficient ofϕ−5.Here,u2,u3,andu5can be expressed by letting the coefficients ofϕ−3,ϕ−2,andϕ0appear.
Becauseu1,u4, andu6are free functions whena(t)=c(t)=d(t)=e(t)orc(t)=d(t)=e(t),the integrability conditions area(t)=c(t)=d(t)=e(t)orc(t)=d(t)=e(t).
Here,we investigate the following vcHSI equation:
It is not difficult to find that Eq.(8) is equal to Eq.(4) whenc(t)=d(t)=e(t)=1.
This article is arranged as follows: In Section 2, the dependent variable transformation and the bilinear operators are introduced,and the bilinear form of the vcHSI equation is obtained with the Hirota bilinear method.In Section 3, the expressions of two-soliton solutions,three-soliton solutions,and four-soliton solutions are studied on the basis of bilinear form.We choose the appropriate parameter values and draw the corresponding figures.In addition,the dynamical behavior of solutions in different planes is analyzed.In Section 4, the long wave limit method is introduced.This method is used to obtain other solutions including lump solution, the interaction of one linear wave and multi-soliton, and the interaction of second-lump solution and kink solution,etc.The corresponding figures are presented to describe the evolution of solutions.In Section 5,the conclusions of this paper can be found.
2.The bilinear form of the vcHSI equation
First of all, we introduce the dependent variable transformation[26]
Substituting Eq.(9) into Eq.(8), we can obtain the bilinear form with bilinear operators as follows:
wherefis the function ofx,y,t;DyDt,Dx2, andDx3Dtare bilinear operators as follows:[11,12]
We now describe the process of assumingf,usingN=1 as an example.Firstly,we assume
wherek1,p1, andare free constants,w1(t) is the function oft,after substituting Eq.(12)into linear terms in Eq.(8)we can reach[31]
Based on the Hirota bilinear method we can assume
whereγ1=k1(x+p1y+w1(t))+γ.Hence, iffis the solution to Eq.(10),theuwe obtained by transformation(9)is the single soliton solution to Eq.(8).
3.The N-soliton solutions of the vcHSI equation
In this section,we introduce the different expressions for solutions to the NLEEs with different values ofNon the basis of bilinear form.[32]
WhenN=2, using the same method on the basis of the single soliton solution,[31]we can obtain
With the help of hirota bilinear method,the expression forfis assumed as follows:
whereγi=ki(x+piy+wi(t))+γ0i,(i=1,2), withki,pi,γ0iandb12being free constants.
Substituting the solution that is obtained by taking Eq.(16) together with Eq.(15) into Eq.(9) into Eq.(8), we will get a system.After solving the system,we can know
Substituting Eq.(17)into the solution and taking the parameters asa(t)=t,k1=−1,k2=1,p1=−3I,p2=3I,γ01=γ02=0, we can get breather waves in the plane.Figure 1 shows the dynamical behavior of the breather waves in(x,y)plane.It is clear that the position of the breather waves changes alongx-axis with time from Figs.1(a)–1(c).However,the amplitude and the waveform of the breather waves keep the same.Figures 1(d)–1(f)are their corresponding density plots.
Without loss of generality, we have chosen another set of parameters to draw the 3D-plots and show them in Fig.2.Whenp1=1−2I,p2=1+2I,γ01=γ02=0, the coefficient functiona(t)is coth(t).We can obtain a set of interactions of soliton solutions and period solutions.Figures 2(a)–2(c)show the change ofufor differentk1andk2.In Fig.2(a),k1=1 andk2=−1.In Fig.2(b),k1=2 andk2=−2.In Fig.2(c),k1=3 andk2=−3.

Fig.1.The breather waves in the(x,y)plane and their density plots.

Fig.2.The interaction of breather waves and soliton solutions in the(x,y)plane and their density plots.
WhenN=3,we can employ the same method to obtain
whereki,pi,andγ0iare free constants.
Substituting Eq.(18) into Eq.(9) and taking the parameters ast=1,k1=2+I,k2=2−I,k3=2+I,p1=−I,p2=I,p3=−I,andγ01=γ02=γ03=0,we obtain the results as shown in Fig.3.Figures 3(a), 3(b), and 3(c) show all the interactions of breather waves, kink solutions, and excitation solutions,and they show the 3D plots whena(t)is taken as different functions.It is obvious that the amplitude of breathers becomes smaller from Fig.3(a)to Fig.3(c).
Next, we choose parametersk1= 1+2I,k2= 1−2I,k3=1+2I,p1=1−I,p2=1+I,p3=1−I,γ01=γ02=γ03=0,and present the corresponding figures on different planes as Fig.4.The coefficient functiona(t) is taken as cost.In the(x,y) plane,tis taken as 0, the solution is the interaction of kink solution and breather waves,as shown in Fig.4(a).In the(y,t) plane,xis taken as 0, the solution is the kink solution,as shown in Fig.4(b).In the (x,t) plane,yis taken as 0, the solution is the interaction of kink solution and breather waves,as shown in Fig.4(c).
WhenN=4,the expression forfis
where
withki,pi,andbeing free constants.
Substituting Eq.(20)into Eq.(9)and taking the parameters ask1=1,k2=2,k3=3,k4=4,p1=−2,p2=1,p3=−1,p4=1,====0,for the coefficient functiona(t)taken as sinht,we obtain the profiles at different times,as shown in Fig.5.It reflects the change in multiple solitons.

Fig.3.The interaction of breather waves,kink solutions and excitation solutions in the(x,y)plane at(a)a(t)=cosht,(b)a(t)=cost,(c)a(t)=t.

Fig.4.The interaction of breather waves and kink solutions in different planes.

Fig.5.The multi-soliton solutions in(x,y)plane.
4.The lump solutions of the vcHSI equation
In this section,the long wave limit method is used to solve the solutions.The solutions obtained using this method is generally the lump solutions.The basic idea to this method is taking the limit of the soliton solutions.[32,33]The long wave limit method is now widely used to find multi-lump solutions.Next,we describe the process of solving solutions.
WhenN=2,we have known the expressions forf,wi(t),andb12in the above section.Now,we take the parameters ask1=ε·l1,k2=ε·l2,=I·π,=−I·π, and substitute them into the expressions forb12andwi(t).After expanding them and using Taylor’s formula we can obtain
We choose proper parameters asp1=−4−I,p2=4−I,take the coefficient functiona(t) as ln(t), and put them into the solution we obtained.Figure 6 shows the corresponding results.There are two solitons with different amplitudes that collide with each other.Figures 6(a)–6(c) show the results taken at different times.In addition,the amplitude of the two waves decreases with time.
WhenN=3, this method is used to determine the expression forf.After substituting the parameters as the same asN=2,we can reach
where
withl1andl2being free constants.
We can draw the results as shown in Fig.7, after substituting Eq.(23)into Eq.(9).The parameters are taken ast=1,p1=1−2I,p2=1+2I,p3=0,=0, and the coefficient functiona(t)is chosen ast2/5.Whenk3=0, the solution is second-order lump solution.It is clear that the amplitude of one lump wave remains unchanged, and the amplitude of the other lump wave increases withk3.Finally,whenk3=1.3,the solution is the interaction of kink solution and lump solutions in different planes.
Now,we choose a set of parameters ask3=−2,p1=−I,p2=3,p3=0,=0, and take the coefficient function as sint.The corresponding results are presented in Fig.8.Figures 8(a)–8(c) show the emergence of periodic waves at differentx.Figures 8(d)–8(f) show the annihilation of periodic waves at differentx.Whenx=0, the amplitude of the periodic wave reaches its maximum.
WhenN=4,we use this method to solvef.After some calculations,we can determine the expression forfas follows:
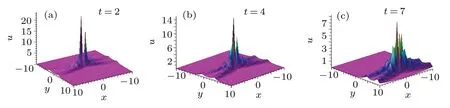
Fig.6.The dynamical behavior of second-order lump solutions with t in(x,y)plane.

Fig.7.The dynamical behavior of second-order lump solutions with k3 in(x,y)plane.

Fig.8.The process of periodic wave emergence and annihilation in(y,t)plane.

Fig.9.The changes of position of second-order lump solution and their density plots.

Fig.10.The interaction of one linear wave and multi-soliton solution in(x,y)plane.
In Fig.9,we choosep1=I,p2=−I,p3=2I,p4=−2I,and take the coefficient functiona(t) ast.We can find that the position of the second-order lump solutions has changed with time.The position of the solution att=5 is same as the position of the solution att=−5.In addition,the amplitude of the second-order lump keeps the same.In Fig.10,we choosep1=1,p2=−I,p3=5I,p4=−5I,and take the coefficient functiona(t)as cott.These solutions are interaction of one linear wave and multi-soliton solutions.The amplitude of multi-soliton changes witht.
5.Conclusions
In summary, we have investigated the Hirota–Satsuma–Ito equation with variable coefficient.We use the WTC method to prove the equation is integrable.We solve its bilinear form with the help of the Hirota bilinear method.TheN-soliton solutions are constructed on the basis of bilinear form.We specifically study the form of the solutions forN= 2,3,4.In addition, we introduce the long wave limit method.The form of the solutions forN=2,3,4 is studied using this method.By selecting appropriate parameters we obtain multiple types of solutions including breather waves solutions,lump solutions,periodic solutions,and the interaction of breathers and periodic solutions, etc.Their corresponding figures are presented to describe the evolution of solutions.
Acknowledgements
This work was supported by the National Natural Science Foundation of China(Grant No.11505090), Research Award Foundation for Outstanding Young Scientists of Shandong Province(Grant No.BS2015SF009),the Doctoral Foundation of Liaocheng University (Grant No.318051413), Liaocheng University Level Science and Technology Research Fund(Grant No.318012018),and Discipline with Strong Characteristics of Liaocheng University–Intelligent Science and Technology(Grant No.319462208).
- Chinese Physics B的其它文章
- Soliton propagation for a coupled Schr¨odinger equation describing Rossby waves
- Angle robust transmitted plasmonic colors with different surroundings utilizing localized surface plasmon resonance
- Rapid stabilization of stochastic quantum systems in a unified framework
- An improved ISR-WV rumor propagation model based on multichannels with time delay and pulse vaccination
- Quantum homomorphic broadcast multi-signature based on homomorphic aggregation
- Orientation determination of nitrogen-vacancy center in diamond using a static magnetic field

