An improved ISR-WV rumor propagation model based on multichannels with time delay and pulse vaccination

Yafang Dong(董雅芳), Liang’an Huo(霍良安), Xiaoxiao Xie(谢笑笑), and Ming Li(李明)

Business School,University of Shanghai for Science and Technology,Shanghai 200093,China

Keywords: rumor propagation,propagation channels,pulse vaccination control,time delay,information base

1.Introduction

With the development of new technologies,various intelligent social networks and new media platforms have gradually become the main way people obtain information.However, while the Internet offers convenience in communicating with people,this has both positive and negative effects.These emerging Internet technologies and social media have also become a breeding ground for the generation and rapid spread of online rumors, bringing new challenges to public safety and long-term social security.Therefore, studying the dynamic process of rumor propagation and control strategies in social networks is of great practical significance for targeted rumor management and alleviating public concern.[1–3]

Research on the rumor propagation process first began in the 1960s, and most of the early classical rumor propagation studies were based on epidemic transmission studies.This is because they have many similarities in terms of transmission modes, transmission characteristics, and classification principles.Daley and Kendall proposed the DK model to study rumor propagation processes in 1965.[4]Subsequently,Maki and Thomson optimized the rules of propagation in the DK model and proposed the MK model.[5]Zanetteet al.applied complex networks to the study of the rumor propagation process for the first time.They established a rumor propagation model based on a small-world network and calculated the threshold of propagation.[6,7]Shanet al.improved the traditional scalefree network according to the complex network theory and the actual characteristics of shared social networks,and proposed a network topology model in line with the characteristics of shared social networks.[8]

In recent years, some scholars have applied epidemiological dynamics to study the dynamic process of rumor propagation from different perspectives.[9–13]Xiaet al.proposed a new ILSR rumor propagation model by combining an incubation mechanism, a cross-propagation mechanism, and a general nonlinear propagation rate in a multilingual environment.[14]To study the effect of forced silence on spreaders, Zhuet al.proposed a model of rumor propagation on online social networks with silence forcing.[15]Choiet al.proposed a model based on a bidirectional encoder representation from transformers to identify false rumors.[16]Jiaet al.studied the phenomenon of rumor propagation on social networks by dividing rumor propagation channels into group propagation and point-to-point propagation,and found that group propagation in social networks has a greater impact on rumor propagation than point-to-point propagation.[17]In addition, with the refinement of the research, many scholars have noted the important roles of social reinforcement,[18,19]group communication,[20]individual activity,[21]media reports,[22–24]environmental noise,[25]individual psychology,[26]time delay,[27]and rumor type[28]in the rumor propagation process.These studies have greatly enriched the research field of rumor propagation.

The aforementioned studies have explored how individual heterogeneity, group transmission, and network topology influence the mechanisms of rumor propagation mechanisms based on single-layer networks and attempt to provide explanations for the propagation phenomenon.However,in reality,the process of rumor propagation can be affected by multilayer networks.Multi-layer networks mean multiple channels of communication,each represented by a single layer.Multilayer networks can distinguish different communication channels and lay the foundation for qualitative research in different ways, which improves the accuracy and authenticity of system.[29]Considering the influence of individual online and offline interactions,the time-varying structure of the network,and the diversity of individual characteristics on the rumor propagation process, Zhuet al.proposed a more comprehensive model of rumor propagation based on activity-driven networks, and they found that the presence of online communication channels facilitated the spread of rumors and reduced the use of on offline channels for rumor propagation.[30]Donget al.constructed an improved two-layer model considering time delay to describe the dynamic process of rumor propagation in multiple channels.[31]Meiet al.developed a two-layer model to describe two different channels through which people acquire knowledge, and constructed multilayer complex networks based on different ways of acquiring knowledge.[29]Zhuet al.comprehensively considered both online and offline channels to explore the transmission mechanism of a kind of knowledge in a complex network.They found that the transmission efficiency of the two channels not only promoted each other but also competed with each other.[32]

The ultimate purpose of studying the mechanism of rumor propagation is to control its spread and minimize its negative social impact.Many scholars have devoted themselves to exploring strategies to control rumor propagation.[33–35]Keet al.considered using non-smooth control functions to reflect the rebuttal of government and media to rumor propagation, and established a model of reaction-diffusion rumor propagation.[36]Askarizadehet al.proposed a soft rumor control model,in which people avoid the spread of rumors by consulting with trusted friends or reputable authorities.[37]Since control behavior is generally discrete behavior rather than continuous behavior, pulse control has been introduced in the study of the control of rumor propagation.[22,38]Compared with continuous control, pulse control has more advantages in saving resources.In the past, the most prevalent channel used to spread rumors was word of mouth, but this channel was limited by time and space,which limited the spread of rumors to within small groups.However,with the emergence of social media,rumors are no longer limited to a single channel,but are widely spread through social media in the form of text or videos,which makes them more influential.Therefore,the study of the dynamic process of multi-channel rumor propagation has received increasing attention, and this is the main issue discussed in this study.

Based on the above considerations, the main purpose of this paper is as follows: firstly,the existing classical dynamic model is extended and an improved model of rumor propagation based on system time delay considering three communication channels are established, and the effects of different communication channels on the dynamic process are analyzed.Secondly,the threshold condition for the continuous spread of rumors is analyzed,and the stability of the equilibrium points of the system is proved.Then, an optimal control problem is designed and the optimal control conditions are obtained by using Pontryagin’s principle.Finally, the correctness of the theoretical analysis is verified by numerical simulations and a practical application, and the influence of different channels and time delay effects on the process of rumor propagation are discussed,respectively.

The remainder of this paper is arranged as follows.Section 2 introduces the model presented in this paper.In Section 3, the existence of equilibrium points of the model is proved,and the basic reproduction number is obtained by using the next-generation matrix method.In Section 4, the stability of equilibrium points is proved.In Section 5,the control variables and objective functions of the model are determined,and the optimality conditions of the optimal control are given according to Pontryagin’s minimum principle.In Section 6,a numerical simulation is carried out to verify the validity of the results.In Section 7, a practical application is used to verify the validity of the model in this paper.We conclude in the last section of the paper.

2.Model formulation

With the advent of the era of self-media, the channels available for people to obtain information are becoming richer and more diversified.People can get information not only by communicating with others,but also through the rich information base on the Internet.[29]An information base is defined as a collection consisting of websites,news,social media,and other online resources containing information.Considering the different types of information in the information base,this paper further subdivides the information base into the text information base (such as Twitter, Facebook, WeChat, Zhihu)and the video information base (such as Tik Tok, YouTube).Text information is easy to edit and produce, so it takes less time to add it to the text information base, and there is no time delay effect.Video information needs to be recorded and edited by the producer, so it takes a longer time to add to the video information base; thus, there is a time delay effect.Therefore,we suppose that individuals can obtain information through three channels: contact with other people,the video information base,and the text information base.In this paper,these three channels are represented by a three-layer social network,as shown in Fig.1.

Fig.1.The framework of multilayer complex networks.

In an open community,people are divided into three categories according to their different responses to rumors: ignorant(I), spreaders(S), and stiflers(R).Ignorant people are those who have never been exposed to a rumor.Spreaders are those who receive a rumor and choose to continue propagating it by creating videos, text, or contacting ignorant people.Stiflers are those who have lost interest in propagating rumors or have forgotten about them.The information base is divided into two categories according to the form of the information base: text information base and video information base.In this case, the text rumors in the text information base are denoted byW, and the video rumors in the video information base are denoted byV.[39]The ignorant can be exposed to rumors and transformed into a spreader with a certain probability through three channels: contact with spreaders, browsing text rumors and browsing video rumors.In order to propagate rumors, the spreader can create text rumors and upload them to the text information base such as Twitter and WeChat, or create video rumors and upload them to the video information base such as YouTube and Tik Tok,or communicate with the ignorant to propagate rumors.The spreader may be converted into a stifler over time due to reasons such as losing interest in spreading rumors or forgetting.

In addition,considering the timeliness of rumor propagation,introducing the time delay factor can undoubtedly better describe the characteristics of rumor propagation.On the one hand,it takes some time for spreaders to record and edit videos and add them to the video information base,which will cause a certain time delay effect.On the other hand,individuals will take some time to think and decide whether to believe the information after being exposed to it for the first time, which will cause a certain time delay effect.

Based on the above analysis, and considering the multichannel propagation of rumors and the time delay effect, we establish an improved ISR-WV model based on the classical rumor propagation model.The process of the evolution of rumor propagation is shown in Fig.2,and the remaining parameters are defined in Table 1.

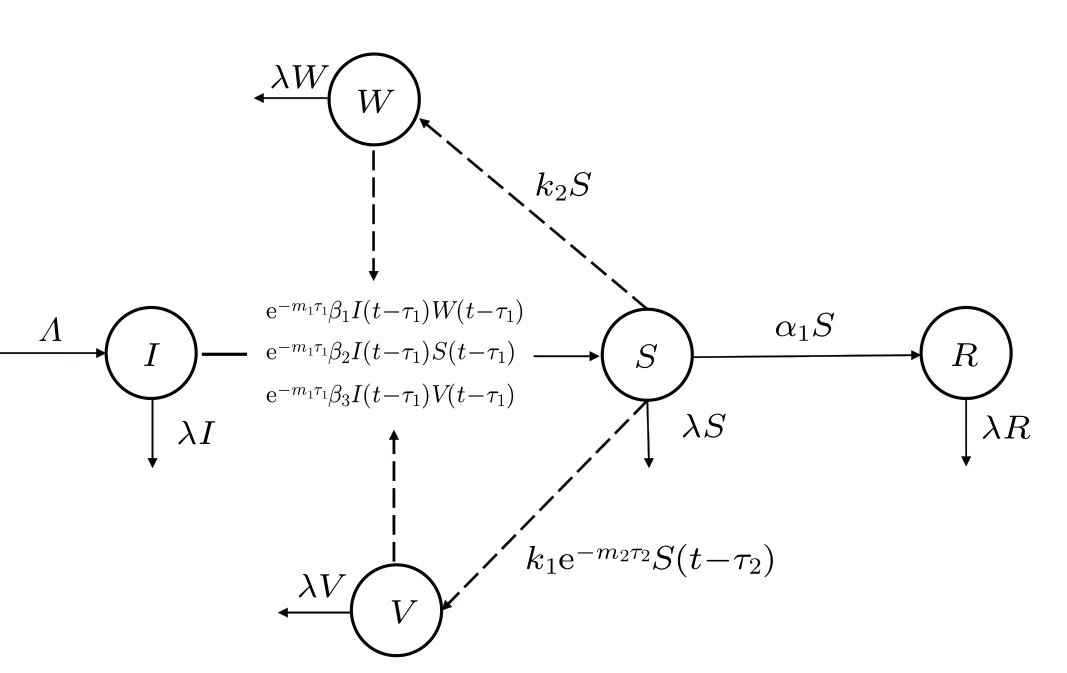
Fig.2.Schematic diagram of multichannel rumor propagation.

Table 1.The implication of the symbols in model(1).

The above parameters take values in the range [0,1].[29]And the rumor propagation rule is assumed as follows:

(1)Assume that an individual enters the community with probabilityΛand moves out of the community with probabilityλ.

(2)Assume that when an ignorant person comes into contact with a spreader, the probability that the ignorant person accepts the rumor and continues to propagate the rumor isβ2.In addition,the ignorant person can be informed of the rumor from the information base,and assume that the probability that the ignorant person comes into contact with a text rumor and transforms into a spreader isβ1, and the probability that the ignorant person comes into contact with a video rumor and transforms into a spreader isβ3.

(3)Assume that rumor spreaders create video rumors with a certain probabilityk1and upload them to the video information base, and create text rumors with certain probabilityk2and upload them to the text information base.Considering the coverage of information and other reasons,we assume that the annihilation rate of rumor information in the information base isλ.

(4)Considering that after the ignorant person is exposed to the rumor,it takes some time to think about whether to continue propagating the rumor or not, we assume that the time delay caused by this thinking time isτ1.The parameterm1indicates the sensitivity of the ignorant to the length of time required to think about the information.In addition, it takes more time for the spreader record and edit to create the video rumor than a text rumor,we assume that the time delay caused by this time isτ2.The parameterm2indicates the sensitivity of the spreader to the length of time required to produce the video.Considering that there is a marginal decreasing effect of time delay on the propagation rate, we use an exponential function to represent the effect of time delay on the propagation process.

(5) With the passage of time, a spreader may convert a stifler with the probability ofα1due to factors such as losing interest in propagating rumors or forgetting about them.

According to the above description,the dynamic ISR-WV model can be expressed in terms of mean-field theory as

The initial conditions of the model take the following form:

whereτ=max{τ1,τ2}andϕ=(ϕ1(θ),ϕ2(θ),ϕ3(θ),ϕ4(θ),ϕ5(θ))∈C([−τ,0],), we denote byC([−τ,0],) the Banach space of continuous functions mapping [−τ,0] into.[22,40–42]

The feasible region of the system satisfies the following closed set:

3.Equilibrium points and the basic regeneration number

In this section,we discuss the existence of the rumor-free equilibrium point and rumor-prevailing equilibrium point of system(1)and calculate the basic regeneration number.

To find the equilibria,the time-independent solutions that satisfy system (1) with the time derivatives equal to zero.Then,the new system is as follows:

By solving system(3),two non-negative equilibrium solutions are obtained:

If the rumor is tending to die out when the system reaches the equilibrium state, i.e., whenS(t) = 0, we can obtainW(t) = 0,V(t) = 0,R(t) = 0,I(t) =Λ/λ.Therefore, the rumor-free equilibrium point of system (1) isE0=(Λ/λ,0,0,0,0).

Before discussing the existence of a rumor-prevailing equilibrium point,we need to find the basic regeneration numberR0of system (1).R0is very important for studying the process of rumor propagation, and the size of the basic regeneration number determines the difficulty of controlling the propagation of the rumor.Based on the next-generation matrix method,[43]we can obtain two matrices as follows:

Thus,

Then, we can obtain the basic reproduction number of system(1)

R0=ρ(FV−1)=R1+R2+R3,

where

Next we discuss the existence of a rumor-prevailing equilibrium point.When rumors persist in the system until an equilibrium state is reached,the rumor-prevailing equilibrium point is denoted byE∗=(I∗,S∗,W∗,V∗,R∗),whereI∗≥0,S∗>0,W∗>0,V∗>0,R∗>0.From Eq.(3)we can obtain

Denote

WhenS=0

and

After proving the existence ofS∗,the next step is to prove its uniqueness.From Eq.(5),we obtain

We get thatGis strictly decreasing at its every zeros.If there is another rumor-prevailing equilibrium point ¯S∗exceptsS∗satisfies thatG′(S∗)≥0,which leads to a contradiction.

Then the proof is completed.

4.The global stability analysis of the equilibrium points

In this section, we discuss the global stability of the rumor-free equilibrium point and rumor-prevailing equilibrium point.

Theorem 2IfR0<1, the rumor-free equilibrium pointE0of model (1) is globally asymptotically stable in a positively invariant setX={ϕ ∈C([−τ,0],R5+):‖ϕ1‖≤x0}.

ProofDefine a Lyapunov function as follows:

Calculating the derivative ofL1(t)along the positive solution of system(1),we have

Obviously, ifR0<1, there will beL1(t)/dt<0.AndL1(t)/dt= 0 if and only ifI(t) =Λ/λ,S(t) = 0,W(t) =0,R(t)=0.Based on LaSalle’s invariant principle,we can obtain the attractiveness of the rumor-free equilibrium pointE0.Therefore, the rumor-free equilibrium pointE0of system (1)is globally asymptotically stable whenR0<1.The proof is completed.

Theorem 3IfR0>1, the rumor-prevailing equilibrium pointE∗of system(1)is globally asymptotically stable.

ProofDefine a Lyapunov function as follows:

whereH(x)=x−1−lnx.

Then calculating the derivative ofL2(t)along the positive solution of system(1),we have

becausek2S∗=λW∗,k1e−m2τ2S∗=λV∗,we can obtain

Thus,we can obtain dL2(t)/dt ≤0,where dL2(t)/dt=0 if and only ifI(t)=I∗,S(t)=S∗,W(t)=W∗,V(t)=V∗,R(t)=R∗.According to the LaSalle’s invariant principle,the rumor-prevailing equilibrium pointE∗of system (1) is globally asymptotically stable forR0>1.The proof is completed.

5.Optimal control strategies

Widespread rumors endanger the harmony and stability of society,and this section discusses ways to control the propagation of rumors.To reduce the negative impact of rumor propagation, the government should strengthen the education of the public on scientific knowledge and improve their ability to distinguish rumors.Popular science education transforms more ignorant people directly into stiflers and reduces the possibility of the propagation of rumors on a large scale.

Regular science education is a discontinuous process,and thus can be seen as a discontinuous periodic pulse intervention.We assume that pulse control affects only the ignorant,and each pulse converts the ignorant into stiflers at a rate ofθ.The stiflers have the knowledge reserve to identify rumors,thus reducing the scale of the propagation of rumors.

Based on the above analysis,the pulse control strategy is proposed according to model(1)as follows:

whereθrepresents the pulse control ratio andtn=nTdenotes the number of thenth science education pulse to the ignorant group.For the analysis,letτ1=τ2=τ.The initial condition of the system is

The allowable control set is as follows:

whereun=θI(t),N −1 are the number of pulses of the system on the interval[T0,TN].

The purpose of controlling the spread of rumors is not only to reduce their negative impact but also to achieve a better control effect with the lowest control cost.Pulse vaccination can promote the conversion of ignorant to stifler, thus reducing the number of spreaders and the social impact caused by rumor propagation.In addition, considering that each pulse control will incur a certain cost,the objective function of this paper is

whereT0=t0,TN=tf,Ais the normal number, which measures the balance coefficient of pulse control consumption.

Considering that there is a case that the control can be controlled once if the control is timely, this section analyzes the optimal control conditions for single pulse control and multiple pulse control separately.

5.1.Single optimal impulse control analysis

From Pontryagin’s principle of minimal values,[44–46]it is known that the optimal control problem of system (14) is the problem of solving for the minimum of the corresponding continuous Hamiltonian and pulsed Hamiltonian functions.Therefore, system (14) and the corresponding objective function(16)for the single-pulse control case are compatible with the continuous Hamiltonian and pulsed Hamiltonian functions,respectively.[47]

wherex=(I,S,W,V,R)T,fi+gi(xτ), (i=1,2,3,4,5) represents the right-hand part of theith equation att ／=nTin system(14)andhi,(i=1,2,3,4,5)represents the right-hand part of theiith equation att=nTin system(14).

Theorem 4If there exists an optimal controlu∗andT∗and a corresponding optimal stateI∗,S∗,W∗,V∗,R∗for system (14) in the case of a single pulse vaccination such that system(14)satisfies

Then there exists an accompanying functiona(t) =(a1(t),a2(t),a3(t),a4(t),a5(t))Tsatisfying

whent ∈[T,tf],we have

whent ∈[tf,tf+τ],we have

and

ProofCorresponding to system(14)we have

Letu∗be the optimal number of pulse vaccinations for system(14),and since only single pulse vaccination is considered at this point, the optimal pulse vaccination time for system(14)isT∗,and the corresponding optimal state quantity isI∗(t),S∗(t),W∗(t),V∗(t),R∗(t).

The continuous and impulsive Hamiltonian functions established from system (14) and the corresponding objective function(15)are

From the extreme value condition,it is obtained that

then we can obtain

Sinceu>0,we have

According to the adjoint equation,whent ∈[T,tf],there is

then we have

whent ∈[tf,tf+τ],we have

According to the cross-sectional conditions,we have

Due to∂P/∂x=0,we have

It follows that the covariance variablesa(t)are continuous.

According to the multiplication operator,we have

Substituting equation (48) into the extreme value conditions(35)and(38),respectively,we get

The proof is complete.

5.2.Optimal control analysis under multiple pulse vaccination

In the case of multiple pulse vaccination, system (14)and the corresponding objective function(15)are compatible with the continuous Hamilton function and the pulse Hamilton function,respectively,

wherefi+gi(xτ), (i=1,2,3,4,5) represents the right-hand part of theith equation at timet ／=nTin system (14) andhi,(i=1,2,3,4,5)represents the right-hand part of theith equation at timet=nTin system (14).Similar to the proof of Theorem 4,Theorem 5 can be obtained as follows:

Theorem 5The necessary condition for system (14) to achieve optimal control in the case of multiple pulse vaccination is

6.Numerical simulations

In this section, we take reasonable values for the parameters in system (1) built in this paper and simulate the above theoretical results using MATLAB to verify their correctness.And further explore the specific effect of control on the process of the propagation of rumors.

Considering the scenario thatΛ=0.25,λ=0.25,β1=0.3,β2= 0.35,β3= 0.35,k1= 0.6,k2= 0.2,α1= 0.35,m1=0.3,m2=0.6,τ1=2,τ2=2,[17,29,48]thenR0<1.SystemI,S,W,V,Revolves with time as shown in Fig.3.From the figure, we can see that the rumor eventually tends to die out and the system finally reaches the steady state.When the parameters are set toΛ=0.118,λ=0.1,β1=0.2,β2=0.4,β3=0.5,k1=0.4,k2=0.1,α1=0.3,m1=0.2,m2=0.02,τ1=1,τ2=1,[17,29,48]thenR0>1.SystemI,S,W,V,Revolves with time as shown in Fig.4.It can be seen that when the system reaches the steady state, the spreaders still exist,indicating that the rumor will continue to propagate.

Fig.3.Diagram of the evolution of time of system(1)when R0<1.

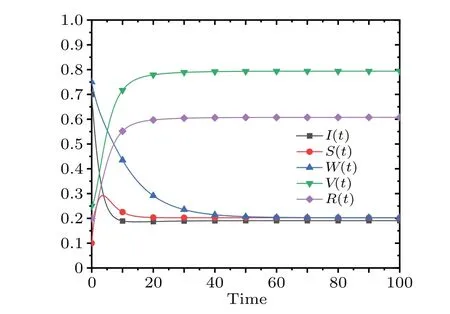
Fig.4.Diagram of the evolution of time of system(1)when R0>1.

Next we analyze the sensitivity of the thresholdR0toβ1,β2, andβ3, as shown in Fig.5, where the magnitude of the value ofR0is indicated by color.It can be seen that the thresholdR0and the propagation ratesβ1,β2andβ3are positively correlated.That is, an increase in the text rumor propagation rateβ1, the contact propagation rateβ2or the video rumor propagation rateβ3increases the value of the thresholdR0.In addition,when the propagation rate of any channel is constant,the propagation rates of the other two channels are positively correlated with the magnitude of theR0value.In particular,when the contact propagation rateβ2is a constant value,R0shows a higher sensitivity to the increase ofβ1andβ3.Specifically, in Fig.5, the color span of the corresponding slice is larger forβ2= 0.5 compared to the other two slices.This indicates that the combined effect of the text rumor propagation rate and video rumor propagation rate has a greater impact on the thresholdR0, which has a greater impact on the rumor propagation process compared to contact propagation.Therefore, in order to better control rumor propagation, we should focus on text rumor propagation channels and video rumor propagation channels, and take corresponding control measures to reduce their propagation rates so that the thresholdR0<1.

Fig.5.Influence of β1,β2,and β3 on threshold R0.

To further explore the specific role played by the propagation rates in the rumor propagation process, we simulated the effects ofβ1,β2, andβ3on the density of spreadersS(t),respectively,as shown in Fig.6.Figure 6(a)portrays the effect of the text rumor propagation rateβ1on the rumor propagation process.It can be seen that the peak of spreader densityS(t)is positively correlated with the size ofβ1, i.e., the largerβ1is,the larger the peak of spreader densityS(t)is.This indicates that the increase in the text rumor propagation rate will promote the further propagation of rumors and expand the scale of rumor propagation.Figure 6(b)portrays the effect of contact propagation rateβ2on the rumor propagation process.It can be seen that the spreader densityS(t) increases with the increase of contact propagation rateβ2, which indicates that the increase in contact propagation will expand the scale of rumor propagation.Figure 6(c)portrays the effect of video rumor propagation rateβ3on the rumor propagation process.It can be seen that asβ3increases, the peak of spreader densityS(t)also increases, indicating that the larger the video rumor propagation rate is, the larger the scale of rumor propagation is.In summary, an increase in the propagation rate of any of the three propagation channels will promote an increase in the scale of rumor propagation, in which the video information base channel has the strongest propagation capacity, the text information base channel the second strongest, and the contact communication channel the weakest.In addition, it can be seen from Fig.6 that in any of the channels, the larger the channel propagation rate is, the longer it takes for the spreader densityS(t) to stabilize.Therefore, relevant departments should take corresponding control measures to reduce the propagation rate of each channel, and focus on the video information base channel and the text information base channel,so as to reduce the scale of rumor spreaders,and make the system quickly reach a stable state.

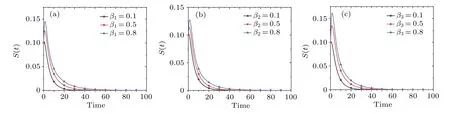
Fig.6.Trajectories of spreader density S(t)at different propagation rates.

Figure 7 shows the comparison of the joint analysis of the propagation probabilities of different models.It can be seen that the multichannel ISR-WV model has the largest spreader density,followed by the ISR-V model and the ISR-W model,and the ISR model has the smallest spreader density.This indicates that compared with the classical ISR model,which only considers single-channel propagation,the increase of channels expands the scale of rumor propagation.And the propagation efficiency of the video rumor information base channel is greater than that of the text rumor information base,which is consistent with the above analysis.

Fig.7.Comparison of propagation efficiency of different models.

Figure 8 depicts the effects of time delaysτ1andτ2on the spreader densityS(t).It can be seen that the spreader densityS(t) is negatively correlated with the time delayτ1, i.e.,whenτ1increases,S(t)decreases accordingly.This indicates that the longer the thinking time required for ignorant people to react to a rumor after acquiring it through any channel,the smaller the rumor propagation scale.Moreover,as can be seen from Fig.8, the effect ofτ2onS(t) depends on the value ofτ1.When is small, it means that people are more credulous.Under this case, the spreader densityS(t) decreases asτ2increases,which indicates that the time required for spreaders to produce video rumors is negatively correlated with the scale of rumor propagation when people are more credulous.Whenτ1is larger,it means that people are more cognizant,in which case the size ofτ2has no significant effect on the spreader densityS(t).Therefore,when people are more credulous,relevant departments should strengthen the review and control of the newly uploaded content in the information base, so as to reduce the negative impact of rumor spreading.

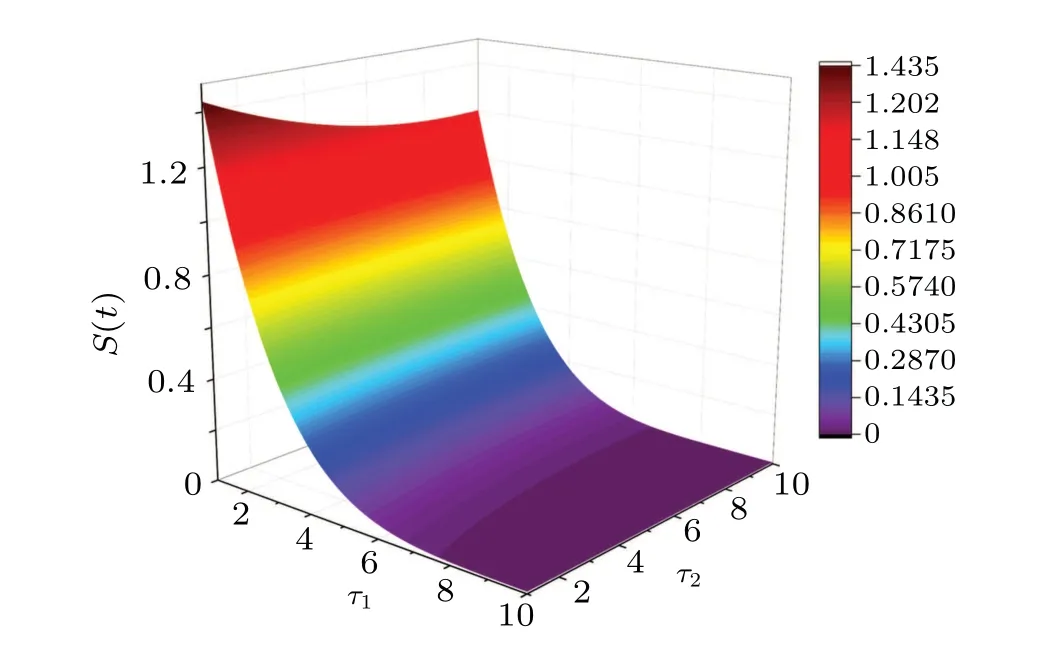
Fig.8.Influence of time delay τ1 and τ2 on the spreader density S(t).

Then we simulated the influence of time delayed impact ratesm1andm2on the rumor propagation process, respectively, as shown in Fig.9.As can be seen from Fig.9(a), the peak of the spreader density decreases with the increase ofm1.It indicates that the impact degree of the thinking timeτ1of the ignorant after receiving the information on their transformation to spreaders is inversely proportional to the rumor propagation scale.As can be seen in Fig.9(b), the peak of spreader density decreases with the increase ofm2,indicating that the greater the impact degree of the timeτ2required by the spreader to produce the video,the smaller the scale of rumor propagation.In addition,the impact ratem1has a greater influence on the rumor propagation process compared tom2,which indicates that the change in the ignorant’s thinking time has a more significant impact on the rumor propagation process than the change in the spreader’s video production time.Therefore,in the reality of rumor spreading process,we can reduce the propagation scale of rumors by adding controls such as science education so that the ignorant can be calmer after receiving rumors and spend more time to identify the authenticity of the information.

Fig.9.Influence of time delayed impact rates m1 and m2 on the spreader density S(t).

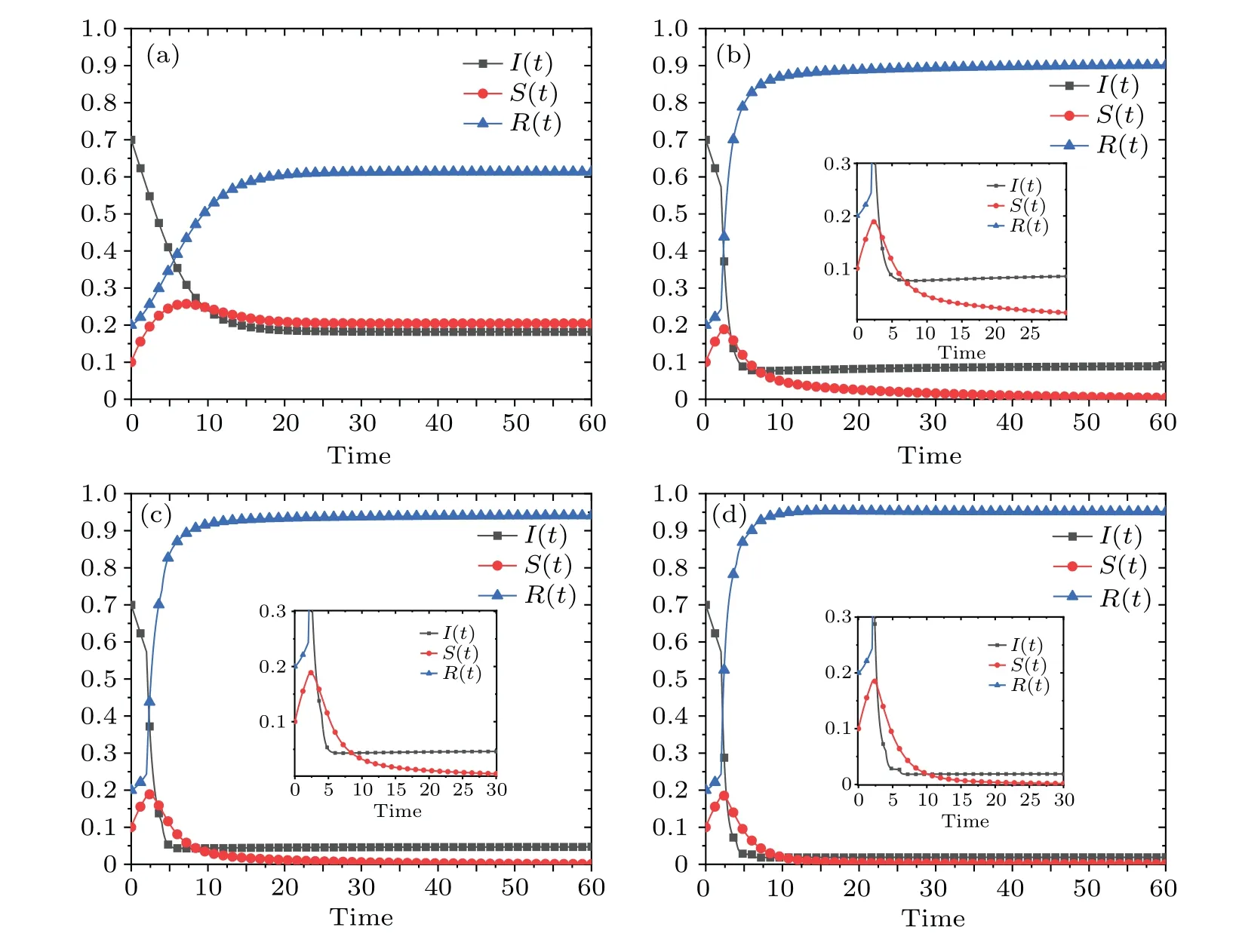
Fig.10.Trajectories of I(t),S(t),and R(t)under different control strategies.

Finally,we simulated the trajectory diagrams of the ignorant,spreader and stifler in the system under different control strategies, as shown in Fig.10.Figure 10(a) shows the trajectory diagrams of the ignorant, spreader and stifler in system (1) in the uncontrolled state, and it can be seen that the final system tends to the steady state.Figure 10(b)shows the trajectory of the single optimal pulse vaccination control,and it can be seen that after the single optimal pulse vaccination control behavior is applied,the ignorantI(t)decreases rapidly and the stiflerR(t)increases rapidly.The peak of the spreaderS(t)decreases, indicating that the single optimal pulse vaccination control can effectively reduce the scale of rumor propagation.In addition,the spreaderS(t)gradually decreases with time and finally stabilizes at 0, which indicates that the rumor is effectively controlled within a short period of time and greatly reduces the damage caused by rumor propagation.Figures 10(c) and 10(d) simulate the trajectories of the system under the 2-pulse vaccination control and 3-pulse vaccination control strategies,respectively.It can be seen that as the number of pulse vaccination increases,the system takes less time to reach a steady state,which indicates that the number of pulse vaccination control has a positive impact on suppressing rumor propagation.However,a larger number of pulses means a higher control cost,so we need to find a balance between the number of pulses and the cost of control to achieve the best control effect.In addition, it is worth noting that the steadystate time shortened by multiple pulses is not as significant as the effect of a single pulse, which indicates that choosing the right pulse timing is crucial to improve the efficiency of rumor control and deserves further in-depth study.

7.Model application

In this section, we compare the model in this paper with the rumor propagation process in the real scenario provided in Ref.[49]to verify the validity of the model.On 2017 December 22,a news story on Sina Weibo about“tourists pulling elephant tails in Thailand and causing the leader of the group to be trampled to death” triggered a heated public discussion and generated negative impacts.The real data is shown in Table 2.

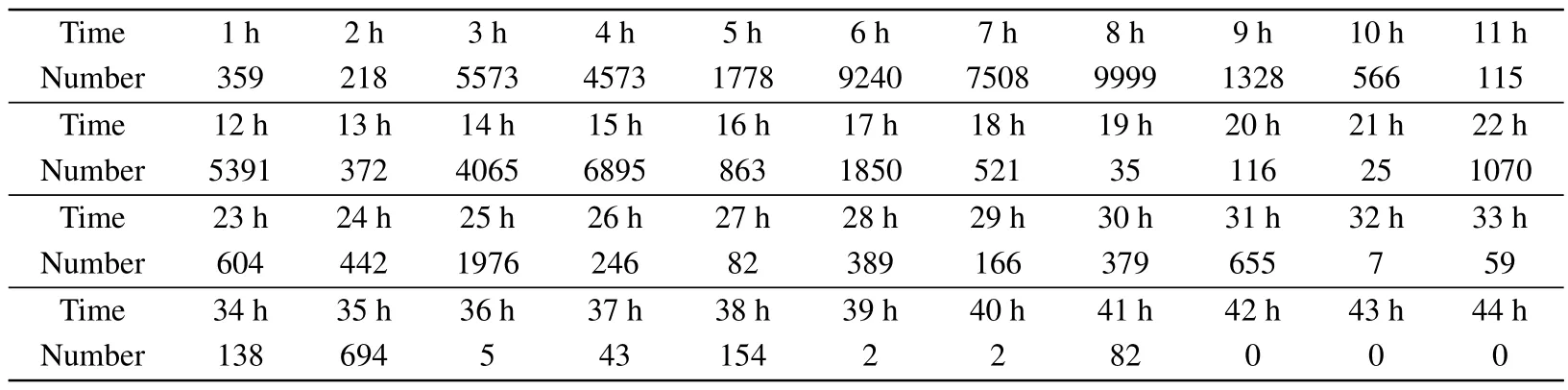
Table 2.The number of spreaders.

Fig.11.The evolution of rumor spreaders and real data.

The real data provided in Table 2 is used to compare with system(1),as shown in Fig.11(a).It can be seen that from the stage of rumor generation to the peak of rumor propagation,the model in this paper matches well with the real situation and can well reflect the process of rumor spreading in the real scenario.However,according to model predictions,if control measures are not taken in time at a later stage,rumors will persist and have a large negative impact.If the control strategy is adopted in time at the 8th hour, the rumor will be controlled until it dies out, as shown in Fig.11(b).This was also verified in the real data, and the rumor was gradually quelled on 25 December of the same year when the Thai police issued an official message that the news was inaccurate and there was no tail dragging to harass the elephants.The results show that the model in this paper can well reflect the real scenario and has some guiding significance in the process of rumor propagation in reality.

8.Conclusion

The channels through which individuals are exposed to rumors are mainly text information base, video information base,and contact with others.Considering the different propagation efficiency of these three propagation channels, an improved propagation model was established by considering three propagation channels and time delays, and further the influence of popular science education pulse vaccination control is considered on the rumor propagation process based on this model.Firstly, the basic regeneration numberR0is obtained by the next generation matrix method,and the stability of the rumor-free equilibrium point and the rumor-prevailing equilibrium point is proved by using the Lyapunov stability theory.Then,considering the popular science education pulse vaccination,the necessary conditions for minimizing the negative impact caused by rumor propagation are obtained by using Pontryagin’s minimum principle.Finally, through numerical simulations, we found that the magnitude of the propagation rate of each channel is positively correlated with the magnitude of the basic regeneration numberR0.In particular, the basic regeneration numberR0is more sensitive to the text rumor propagation rateβ1and the video rumor propagation rateβ3.The value of the thinking timeτ1required for ignorant people to react after being exposed to a rumor is negatively correlated with the scale of rumor propagation.Whenτ1is large enough, it means that people are cognizant enough, in which case the timeτ2required for spreaders to produce a video has a very small effect on the rumor propagation process.Conversely, whenτ1is small means that people are credulous, in which case the timeτ2required by the spreader to produce the video is negatively correlated with the final size of rumor propagation.In addition,well-timed pulse vaccination control for popular science education is effective in controlling rumor propagation,but the choice of the appropriate pulse timing deserves further in-depth study.

Acknowledgements

This work was partially supported by the Project for the National Natural Science Foundation of China (Grant Nos.72174121 and 71774111), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning,and the Project for the Natural Science Foundation of Shanghai(Grant No.21ZR1444100).