北海铁山港填海造陆工程双层地基固结沉降计算应用研究

沈茜丹,张智泰

(1.广西交通设计集团有限公司,广西 南宁 530029;2.广西平陆运河建设有限公司,广西 南宁 530022)

0 引言

2019年广西获批建立广西自由贸易区,经济得到快速发展,在港口、码头、工业基地等开展了吹填造陆施工,吹填后的填筑体呈现典型的双层地基结构,表层土体在日照作用下固结成为硬壳层,下部填筑体缺乏有效排水通道,长时间处于高含水率状态,海相软土双层地基的实际排水情况及固结问题十分复杂,其表现出来的工程特性反映出明显的时空变异性和区域性,严重阻碍了滨海建设的进程[1]。

因此,国内外学者对围海造陆固结问题进行了研究。方开泽[2]采用特征值法求解了一面透水一面半透水以及一面半透水一面不透水这两种情况下的一维固结方程,并绘出计算图便于固结计算的应用。梅国雄等[3]在Terzaghi一维固结理论的基础上,提出了一个从透水到不透水的双面不对称连续排水边界条件,建立了广义Terzaghi固结理论,并给出解答。胡亚元等[4]为研究双孔结构饱和黏土双层地基的一维固结特性,在一维完全侧限条件下根据混合物理论建立了饱和孔隙-裂隙介质的固结控制方程。李林忠等[5]基于Fredlund和Hasan的非饱和土一维固结理论,将非饱和地基假定为双层,引入层间渗流连续条件,得到双层非饱和土地基一维固结控制方程。陈征等[6]建立了分布式排水边界下双层地基二维固结模型,并通过边界转换法、积分变换法和局部离散法给出了相应的半解析解。李红坡等[7]针对吹填土地基内水平排水砂垫层位置的优化问题,考虑双层地基内设置单一砂垫层的情况,采用分离变量法求出了地基超静孔压和平均固结度的解析解答。江雯等[8]推导了土体压缩模量随深度线性变化的双层非均质地基一维固结解析解,然后以渗透系数和压缩系数是深度的多项式函数的非均质地基为例对单层非均质地基的一维固结性状进行了研究。

吹填土上层固结层处于透水-完全不透水之间,下层软弱土具有高压缩性、低渗透性等特点,而其上覆硬壳层具有低压缩性,低渗透性等特点,实际排水情况及固结问题十分复杂,目前尚未有相应的计算模型。本文提出了考虑连续排水边界条件的改进双层地基固结理论数值解,引入可控制排水边界,将上层固结层等效成半透水层,通过与广西北海铁山港软土填筑陆地实际工程监测数据进行验证分析,验证计算方法正确性,所得结论可为沿海填海造陆固结分析提供科学指导。

1 工程概况

本文以北海铁山港为研究对象。北海铁山港为一个椭圆形的盆地,水深的分布特征为从湾口以及沿岸中西部逐渐加深,水深范围一般在20～50 m,平均水深约为38 m,在湾口局部水域可达60 m。本文试验用土样取自北海铁山港某填海造陆场地。该土体呈黑灰色,含少量有机质及海洋生物杂质。根据其基本物理指标,该海积软土定义为淤泥质黏土。填筑造陆土层基本物理性质如表1所示。

表1 计算参数表

2 双层地基模型

为了简化计算,提出以下Terzaghi一维固结理论基本假设:

(1)海相软土是均质的、完全饱和的。

(2)土粒和水是不可压缩的。

(3)在土层在压力作用下,只沿一个方向发生压缩,且水沿着同一方向渗出。

(4)水的渗流服从达西定律。

(5)在渗透固结中,土的渗透系数和压缩系数都是不变常数。

(6)外荷载为两级均速施加。

在满足上述双层地基固结方程假设的前提下,代入连续排水边界条件,求解双层地基固结方程。如图1(a)所示为求解考虑连续排水边界条件的改进双层地基固结理论计算简图。取地表为坐标原点,图1(a)中q(t)为任意加载函数,h1、h2、Es1、Es2、k1、k2分别为上层土和下层土的厚度、压缩模量、渗透系数。荷载简化分两级施加,q1、q2分别是一级、二级荷载增量,如图1(b)所示。

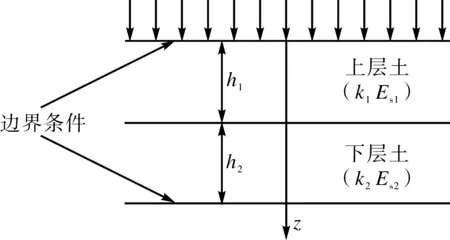
(a)双层地基计算

故可得到双层地基一维固结微分方程:

(1)

(2)

式中:u1,u2——第一/二层超孔隙水压力;

cv1cv2——第一/二层土固结系数。

其中:

可将式(1)、式(2)中孔压用有效应力进行表示,换算为:

(3)

(4)

初始条件:

σ′1,2(z,0)=0

(5)

边界条件:

σ′1(0,t)=q(t)-q(t)exp(-bx)

(6)

σ′2(h1+h2,t)=q(t)-q(t)exp(-ct)

(7)

层间连续条件:

σ′1|z=h1=σ′2|z=h1

(8)

此边界条件为连续排水边界条件,b、c为与土体排水性质相关的参数,详见表2。

表2 参数b、c取值说明表

流量连续条件:

(9)

即式(3)～(9)组成本文考虑连续排水边界条件的改进双层地基固结理论方程。将式(3)～(9)进行拉普拉斯变换:

(10)

(11)

(12)

(13)

(14)

(15)

(16)

由式(10)～(12)得到式(3)、式(4)在拉普拉斯变换域的通解为:

(17)

(18)

其中:

将式(13)～(16)代入式(17)(18)得:

(19)

其中:

q(t)通过图2(b)可表达为:

(20)

将A11、A12、A21、A22带入式(17)、式(18)后进行Laplace逆变换即可得到固结方程式(1)、式(2)的解。但是对于复杂的Laplace解难以进行Laplace逆变换,需要运用Laplace逆变换的数值解法求解。根据已有文献可知,Stehfest算法具有较好的稳定性,并且具有计算参数少的优点。在此选用Stehfest算法编写相应程序对式(17)、式(18)进行数值反演,即:

(21)

随后可计算得到双层地基总固结沉降为:

(22)

双层地基平均固结度为:

(23)

3 模型验证分析

现选用北海铁山港填海造陆某个工程断面进行固结沉降计算。该断面上层为2～3 m的硬壳层,高液限软塑状含砂黏土,压缩模量较高,可达15～20 MPa,渗透能力较差,仅为3×10-6～4×10-6cm/s;下层为厚5～10 m的软土层,含砂软土层压缩模量较低,仅为4.5～8 MPa,渗透系数较差,为2×10-6～3.5×10-6cm/s,软土层下伏基岩为印支期花岗岩。经讨论后决定将硬壳层换为中风化花岗岩(Es=1 200 MPa,ks=5×10-2cm/s)。具体计算参数如表3所示。随后进行堆载预压,并持续监测205 d。

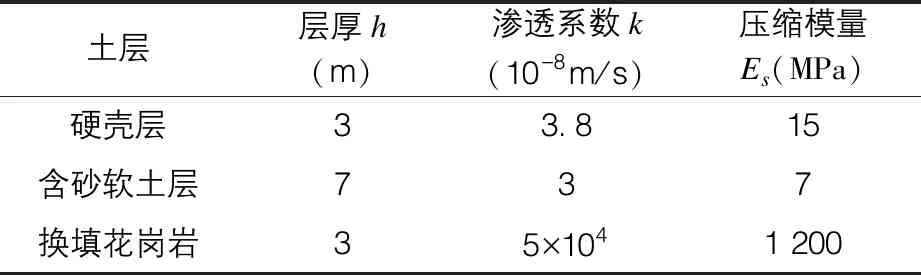
表3 计算参数表

显而易见,该断面上层土不论是硬壳层还是回填土层,其透水边界并非完全透水边界,也并非完全不透水边界,而是一种半透水边界。同时,由于岩土具有较强的离散性,通过调整本文理论模型中边界参数b、c可以有效地预测该类软土地基的固结沉降。

在现场埋设沉降盘,对路基沉降和固结度进行监测。

采用本文提出公式,通过调整参数b、c得出,b=100、c趋于0时,可较好地模拟该监测断面的固结沉降。将计算沉降与实测沉降绘于图2。由图2可知,实际荷载为多级加载,本文方法将加载方式简化为二级荷载。采用换填后的材料进行计算,所得沉降曲线与实测沉降点发展趋势基本一致,表明本文方法适用于分析类似具有硬壳层的软土地基。

在填海造陆中,相对于地基沉降,更应关注固结度的变化情况。将计算得到的固结度与实测固结度情况绘制如图3所示。由图3可知,计算固结度变化与实测固结度变化基本一致,在第205 d时,计算固结度与实测固结度大致在55%。

图3 计算固结度与实测固结度对比曲线图

由图3可知,前期因吹填土逐渐升高,固结度与填土厚度高度相关,呈现阶梯上升趋势,到达固结中后期,排除填土干扰,固结度呈现线性上升趋势,本文所推导的计算结果与实际测量结果较为吻合。因此,以本文方法进一步计算换填前地基固结沉降及固结度随时间变化情况,与换填后地基固结沉降及固结度随时间变化情况进行对比分析,研究换填前后地基性能改善情况。在此为方便分析,换填前后除第一层土性质不同以外,其余条件一致。

通过采用本文提供方法计算换填前后沉降量及固结度变化如图4、图5及表4所示。由图4可知,换填后地基沉降量大幅降低,205 d后沉降相差21.5 mm。由图5可知换填后地基相同时间下固结度有所提高,而且随着时间增长,换填前后固结度相差逐渐明显,在205 d时,固结度相差约12%。结合图4～5,表明换填后地基性能得到了相应的改善。

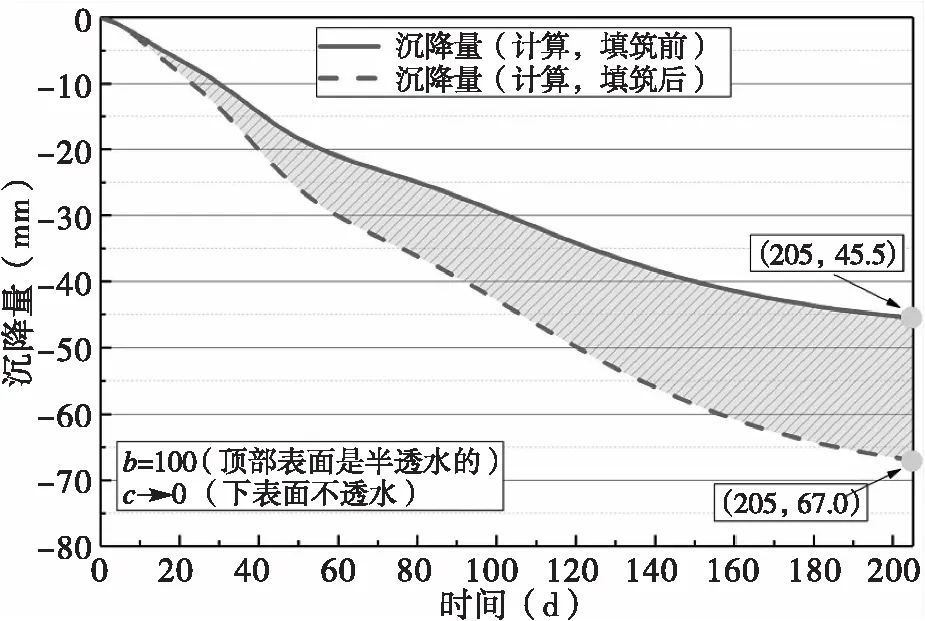
图4 填筑前后沉降量对比曲线图

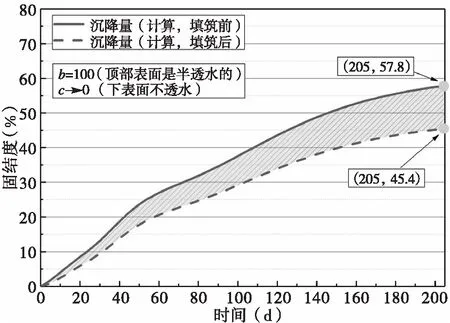
图5 填筑前后固结度对比曲线图

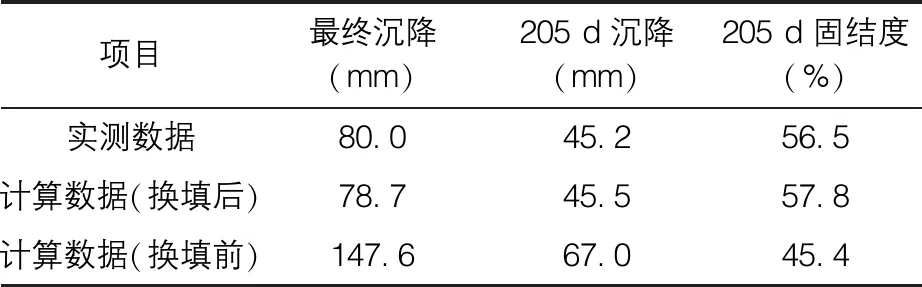
表4 分析结果表

4 结语

本文以复杂排水条件下吹填软土双层地基为研究对象,将连续排水边界条件理论引入双层地基固结理论模型,并采用拉普拉斯变换法则及Stehfest算法,对双层地基固结理论进行求解,并将计算结果与北海铁山港吹填软土吹填造陆现场实测数据进行对比,得出以下结论:

(1)针对吹填软土的双层地基结构,考虑复杂排水边界条件,考虑硬壳层下的连续排水边界条件,改进了现有的双层地基固结模型理论模型。

(2)采用本文提出的改进双层固结理论模型对广西北海铁山港吹填实际工程案例进行计算分析,并与实测数据进行相比,计算误差为0.7%～2.3%,而205 d计算固结沉降及固结度与实测结果误差分别为21.5 mm和12%。所得结果与实测结果基本一致,表明本文理论模型适用于具有硬壳层吹填软土地基固结沉降的分析,而且适用范围广。

(3)采用本文提出理论模型分析了依托工程吹填软土路基换填前后固结沉降和固结度的差异,表明相同时间内换填后地基沉降量降低,固结度提高,地基性能得到较大改善。