L型阵列内插区域对称扩展波束形成
梅笑冰 马社祥
(天津理工大学电气电子工程学院 天津 300384)
0 引 言
在阵列天线波束形成技术的发展中,阵列内插变换技术[1]可实现一定数量阵元的功能仅通过更少的实际阵元,并保持良好的波束形成和输出SINR性能。对于阵列天线的内插变换技术,最早在1990年由Friedlander提出[2],然后将其应用于DOA估计,用较少的阵元实现了更多阵元的DOA估计的功能[3]。但经典内插变换存在角度敏感的问题,即当信号落在内插区域外或内插区域过大时扩展阵列的性能变差。Li等[4]在角度敏感的问题上进行了基于阵列流形长度的虚拟天线波束形成的研究,但较大的插值步长也会使得变换误差有所增加。针对内插变换误差的问题,胡丹婷等[5]对虚拟阵列的变换误差进行权值约束处理,增加了内插变换波束形成的插值角度范围。Blomberg等[6]在圆弧阵列采用了内插变换技术,实现了实际弧形阵列转换为虚拟线性阵列的波束形成研究,但其方位角分辨率较低。Lee等[7]提出一种插值接收信号的功率校准方法,并将其应用到汽车雷达DOA估计,改善了内插精度和DOA估计性能。同年,窦慧晶等[8]基于L型阵列内插变换进行PM算法的改进,实现了较好的二维DOA估计。但关于二维阵列的内插变换波束形成的研究目前较少。
对角加载技术可一定程度地改善波束形成的稳健性,最早由Cox等[9]提出,但也会引起主瓣展宽和零陷变浅。周龙等[10]将改进的对角加载算法应用于线型内插扩展阵列,有效地扩展了阵列孔径并加深零陷。可变对角加载在对角加载的基础上,自适应地改变对角加载的值。Gu等[11]便提出一种可变对角加载的方法,其自适应的加载量较固定对角加载有效改善波束形成。Li等[12]将可变对角加载技术与协方差矩阵锐化技术进行结合,实现了波束形成的零陷展宽,且Song等[13]在可变对角加载的研究中,在权向量中加入了一个可变的对角加载项,获得较好的波束形成性能。Zhuang等[14]以及金桐之等[15]先后采用低复杂度可变对角加载技术,都是对协方差矩阵的特征值进行替换,获得较好的波束形成性能,但此方法仅应用在了实际阵列中。
本文基于L型阵列虚拟扩展,针对经典内插变换的角度敏感问题,提出一种内插区域对称扩展优化的波束形成算法。该算法将阵列流形矩阵关于内插区域坐标轴作对称处理,并在低复杂度可变对角加载的基础上改进,构造新的加载值,然后对可变对角加载改进后的权矢量做Taylor锥化,扩大了可用内插角度的范围,有效改善了角度敏感问题,并且经过优化,提高了L型扩展阵列的波束形成及输出SINR性能。
1 L型阵列内插区域对称扩展模型
一个均匀L型实际阵列,其x轴上阵元数为M,y轴上阵元数为N,阵元间距为1波长,阵列模型如图1所示。
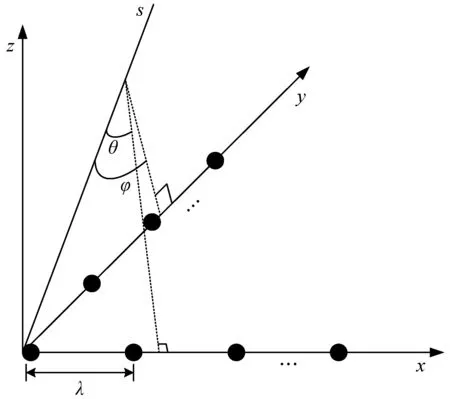
图1 L型阵列模型
不相关的K个远场窄带信号分别从(θ0,φ0),(θ1,φ1),…,(θK-1,φK-1)方向到达此阵列,信号与噪声之间互不相关,噪声为独立的高斯白噪声,t时刻该阵列接收的数据设为:
X(t)=AS(t)+n(t)
(1)
阵列的输出数据是所有阵元的加权和:
y(t)=WX(t)
(2)
式中:W=(w1,w2,…,wM+N-1)为加权矢量,前M个元素对应x轴上M个阵元的权系数,因坐标原点处阵元由x轴与y轴共有,W的后N-1个元素对应y轴上第2到第N个阵元的权系数。
对应于传统内插变换虚拟扩展方法,本文的内插区域对称扩展过程为:将扫描区域根据象限分为四个区域i、ii、iii和iv,如图2所示,对区域i做对称处理分别得到区域ii、iii和iv内的阵列流形矩阵,并对四个区域采用经典内插变换分别进行虚拟扩展,最后采用多区域内插[16]的思想实现总区域的虚拟扩展。
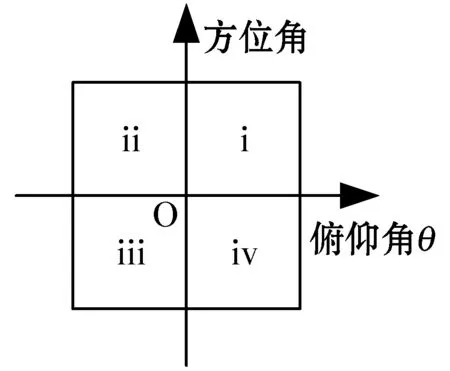
图2 内插区域对称
图2中,区域i的俯仰角的插值范围表示为[θa,θb],方位角的插值范围表示为[φa,φb],则区域i内的实际阵列流形矩阵表示为:
Ai=[ai(θa,φa),ai(θa,φa+Δφ),…,ai(θa,φb),
ai(θa+Δθ,φa),…,ai(θa+Δθ,φb),…
ai(θb,φa),ai(θb,φa+Δφ),…,ai(θb,φb)]
(3)
其中,对应角度(θk,φk)的矢量元素表示为:
(4)
在区域ii内,式(4)关于纵坐标对称的矢量表示为:
(5)
可见,区域ii和区域i内实际阵列流形矩阵的前M行元素互为共轭,后N-1行元素相同,将Ai的前M行元素表示为Ai_M,后N-1行元素表示为Ai_N-1,则区域ii与i内实际阵列流形矩阵的关系可表示为:
(6)
式中:*表示共轭。同样的方法可求得区域iii和区域iv内的实际阵列流形矩阵分别为:
(7)
(8)
(9)
(10)
(11)
分别计算四个内插区域内的转换矩阵为:
(12)
则可将总区域内的变换误差矩阵表示为:
(13)
变换误差为:
(14)
用RX表示X(t)的协方差矩阵,RSS表示期望和干扰信号的协方差矩阵,RN表示高斯白噪声的协方差矩阵,则区域i内虚拟协方差矩阵为:
(15)
对式(15)进行预白化色噪声处理:
(16)
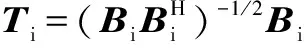
根据多区域内插,对四个区域虚拟协方差矩阵做平均计算,则总区域内的虚拟协方差矩阵为:
(17)
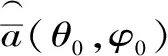
(18)
2 可变对角加载改进及Taylor锥化
(19)
式(19)对应虚拟波束形成权矢量为:
(20)
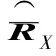
(21)
对式(21)特征值进行修正处理:
(22)
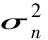
(23)
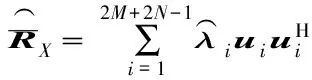
(24)
(25)
式中:∘表示Hadamard积。
3 仿真分析
对本文算法进行计算机仿真分析。仿真条件为:L型实际阵列阵元数M=N=8,阵元间距为1波长,虚拟扩展阵列的阵元数M′=N′=16,阵元间距半波长,各阵元间相互独立无互耦。设期望信号DOA为θ0=φ0=0°,输入信噪比SNR=10 dB,一个独立干扰信号的角度为θ1=φ1=30°,输入干噪比INR=10 dB,快拍数为200。内插变换的插值步长为0.1°,俯仰角与方位角的内插角度范围始终相同。
1) 仿真实验1:内插变换误差分析。根据式(14),内插角度从0°~100°,每隔10°进行一次误差计算,本文内插区域对称扩展与经典内插的插值误差对比如图3所示。
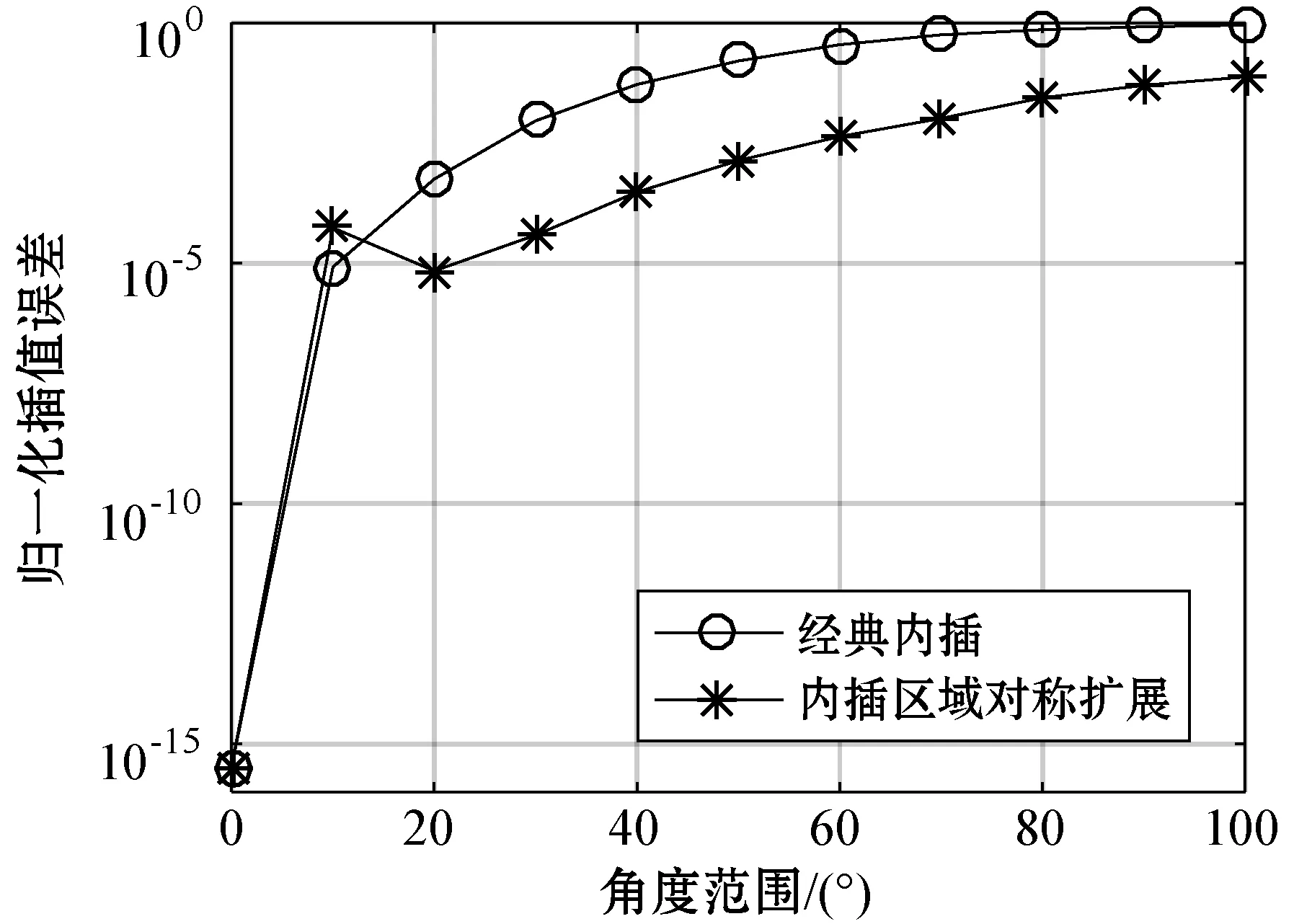
图3 变换误差对比曲线
如图3所示,内插区域对称扩展与经典内插的插值误差均随内插角度的增大而增大,内插角度在10°左右时,内插区域对称扩展的插值误差较大,但仍处于允许范围内,在其他角度上,内插区域对称扩展的误差均小于经典内插。系统可允许的虚拟扩展阵列要求误差不大于10-3,在要求范围内,经典内插的角度可达到20°,但内插区域对称扩展的角度可达到40°,在满足内插误差的要求下扩大了允许的插值角度。
2) 仿真实验2:验证本文算法的波束形成性能。在允许的插值角度下,内插区域对称扩展与经典内插的波束形成对比如图4和图5所示。
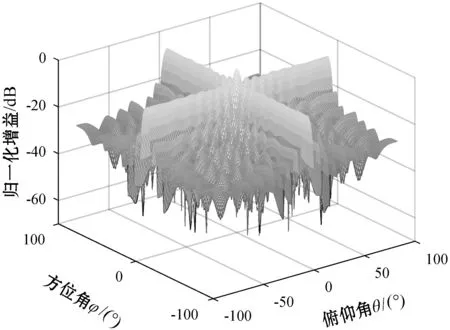
图4 内插区域对称扩展波束形成
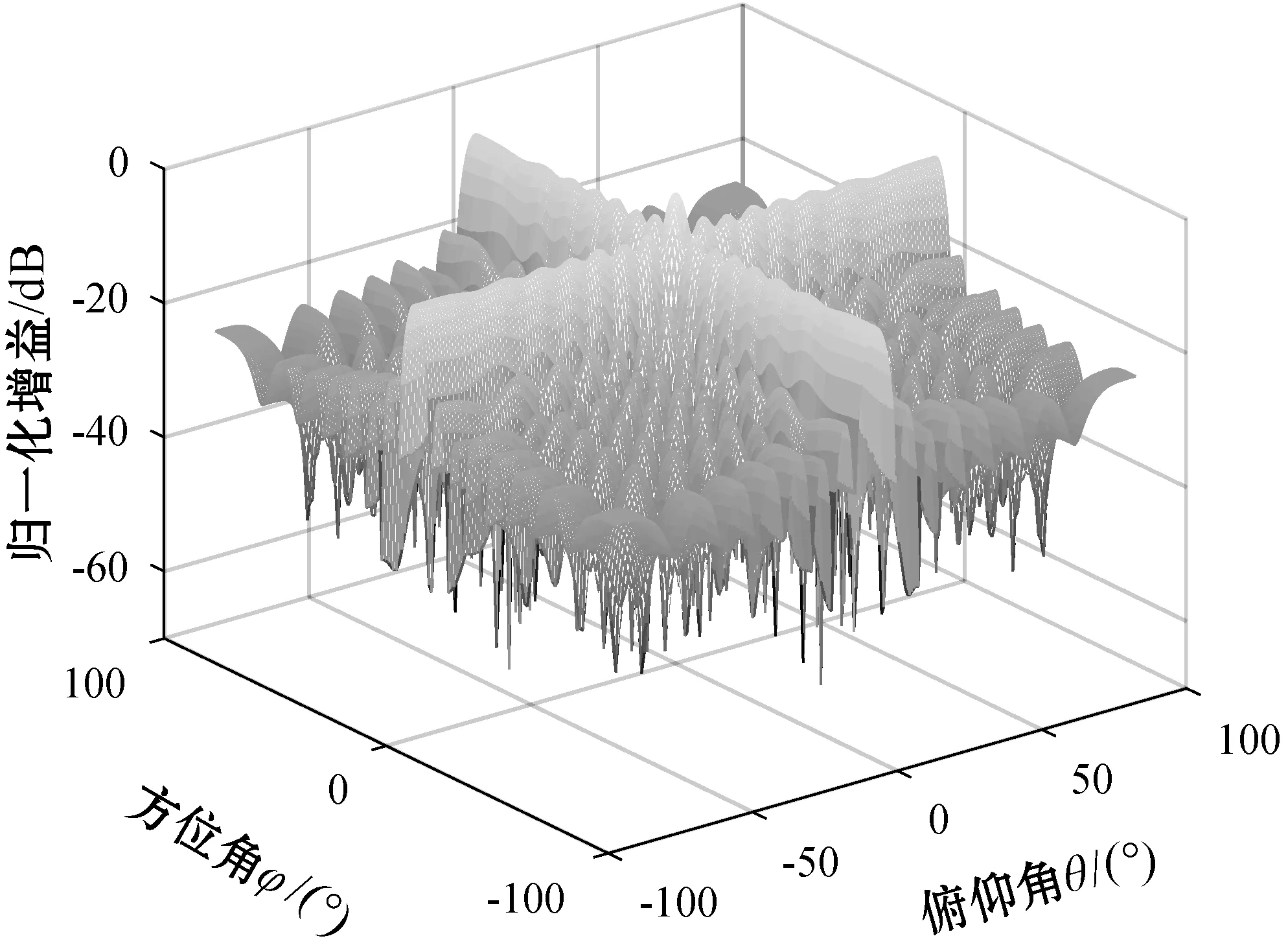
图5 经典内插波束形成
从图4和图5可知,在保证内插角度处于允许最大范围的情况下,内插区域对称扩展与经典内插波束形成主瓣均能对准期望信号方向,内插区域对称扩展的旁瓣略低,峰值更接近于-30 dB,可见,内插区域对称扩展方法在改善角度敏感问题的基础上,对噪声抑制也有一定的改善。
对经典内插做同样的可变对角加载改进与Taylor加权优化,本文内插区域对称扩展优化算法与经典内插优化的波束形成对比如图6和图7所示。
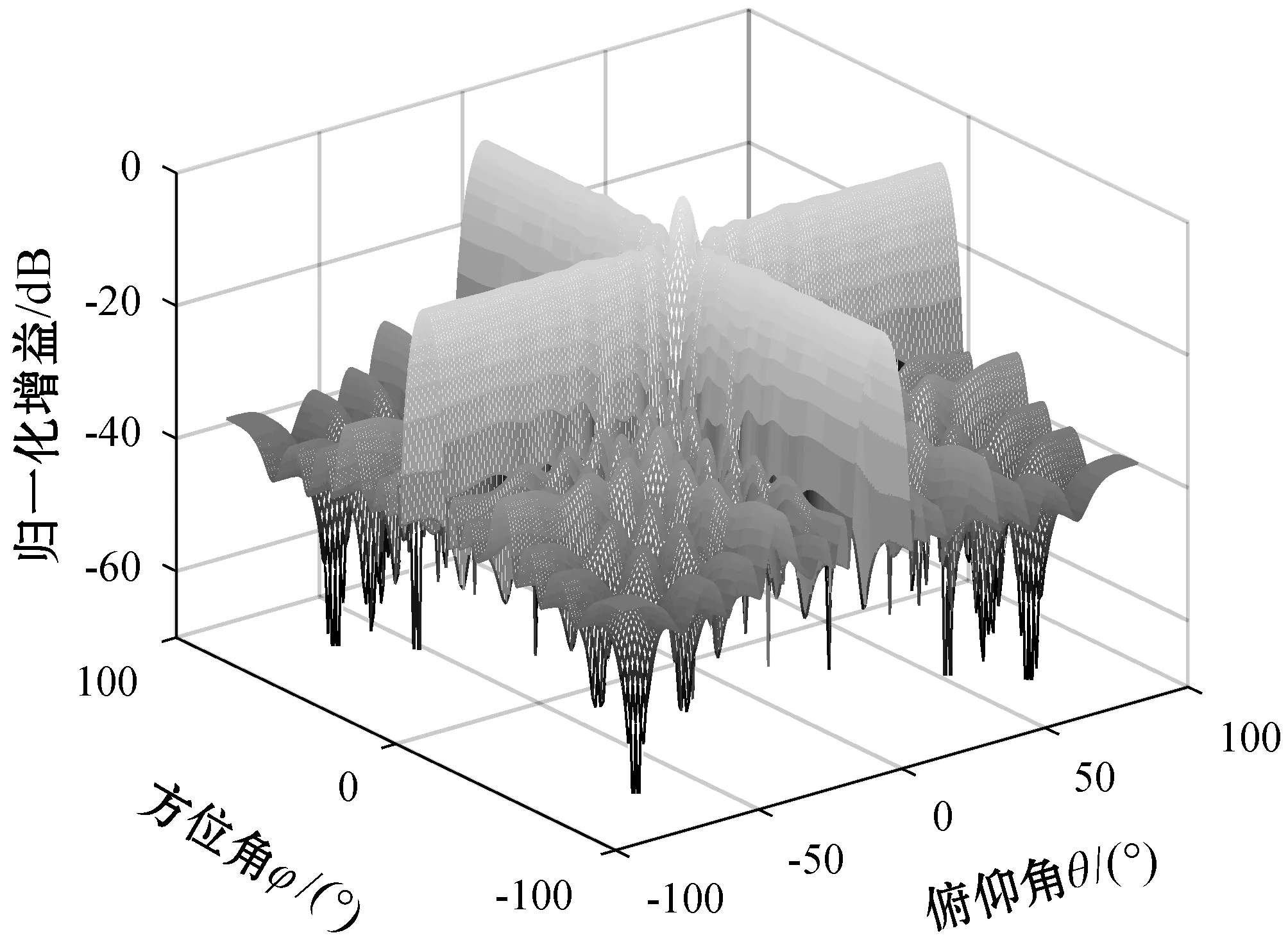
图6 内插区域对称扩展优化波束形成
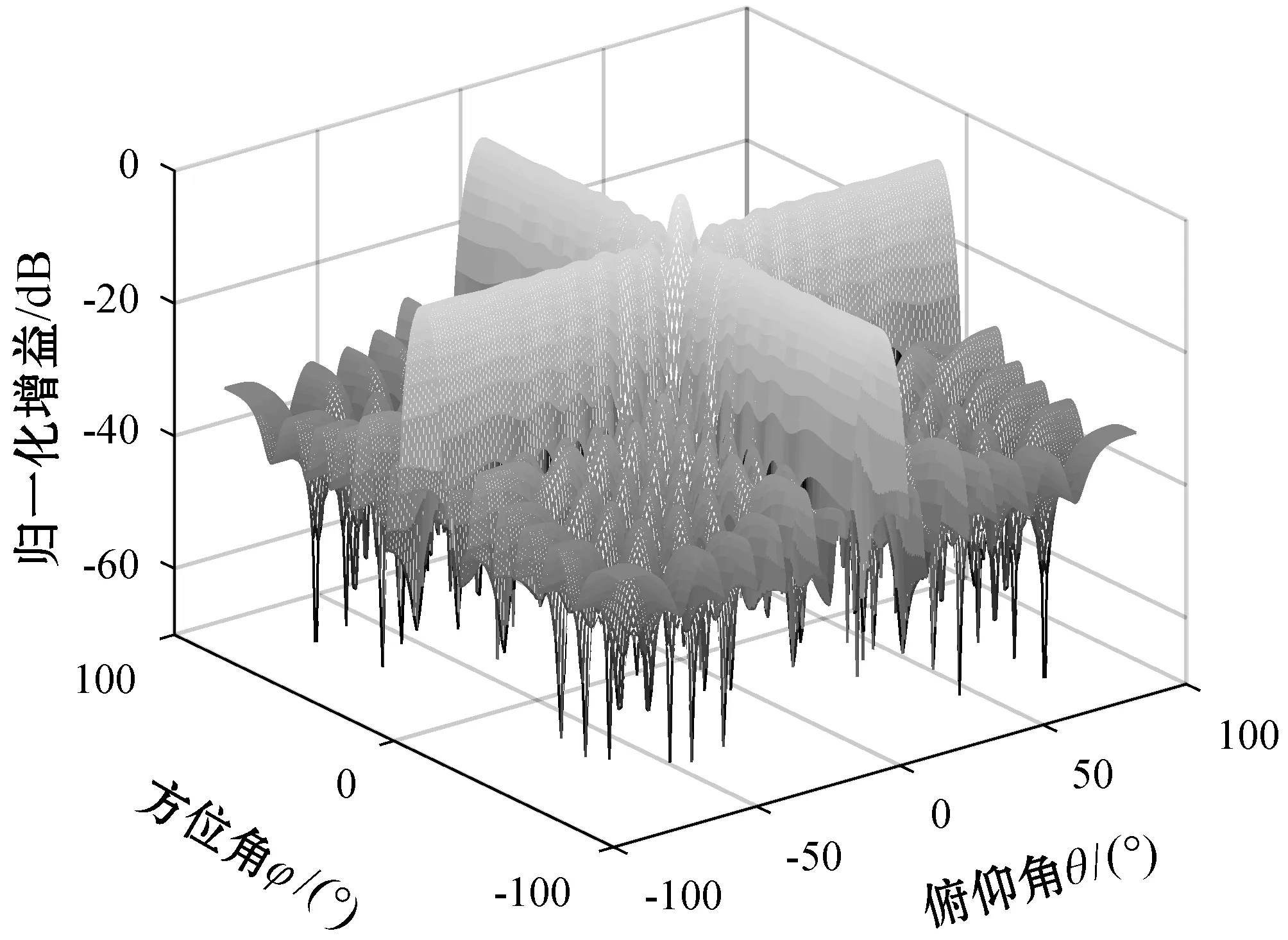
图7 经典内插优化波束形成
在图6和图7中,两者主瓣均能够对准期望信号方向,且副瓣与零陷均得到降低;内插区域对称扩展优化波束形成的旁瓣峰值更接近于-40 dB,低于经典内插优化。可见,可变对角加载改进与Taylor锥化处理对内插区域对称扩展的优化效果更好。
在实际L型阵列中采用文献[17]中导向矢量对称扩展的虚拟天线算法,波束形成如图8所示。
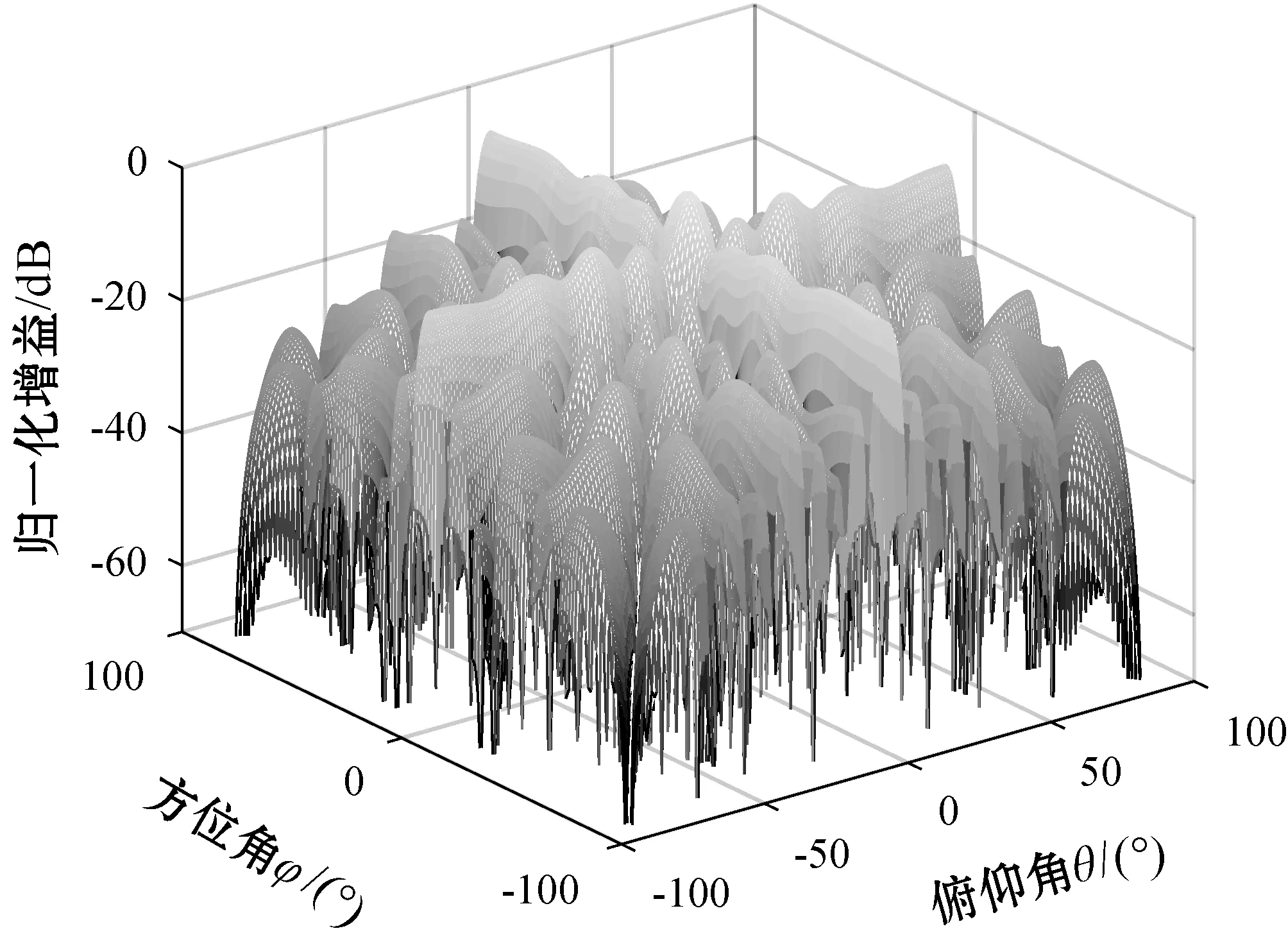
图8 导向矢量对称扩展波束形成
可以看出,主瓣能够对准期望信号方向,但旁瓣较高。图6与其相比,内插区域对称扩展优化波束形成的旁瓣抑制更为明显,但零陷深度较浅。可见,本文内插区域对称扩展优化算法对噪声的抑制性能优于导向矢量对称扩展。
3) 仿真实验3:验证本文算法的输出SINR性能。将输入SNR进行变化,范围由-15 dB到25 dB,上述其他仿真条件不变,内插区域对称扩展、经典内插、内插区域对称扩展优化、经典内插优化以及导向矢量对称扩展的输出SINR随输入SNR变化曲线如图9所示。
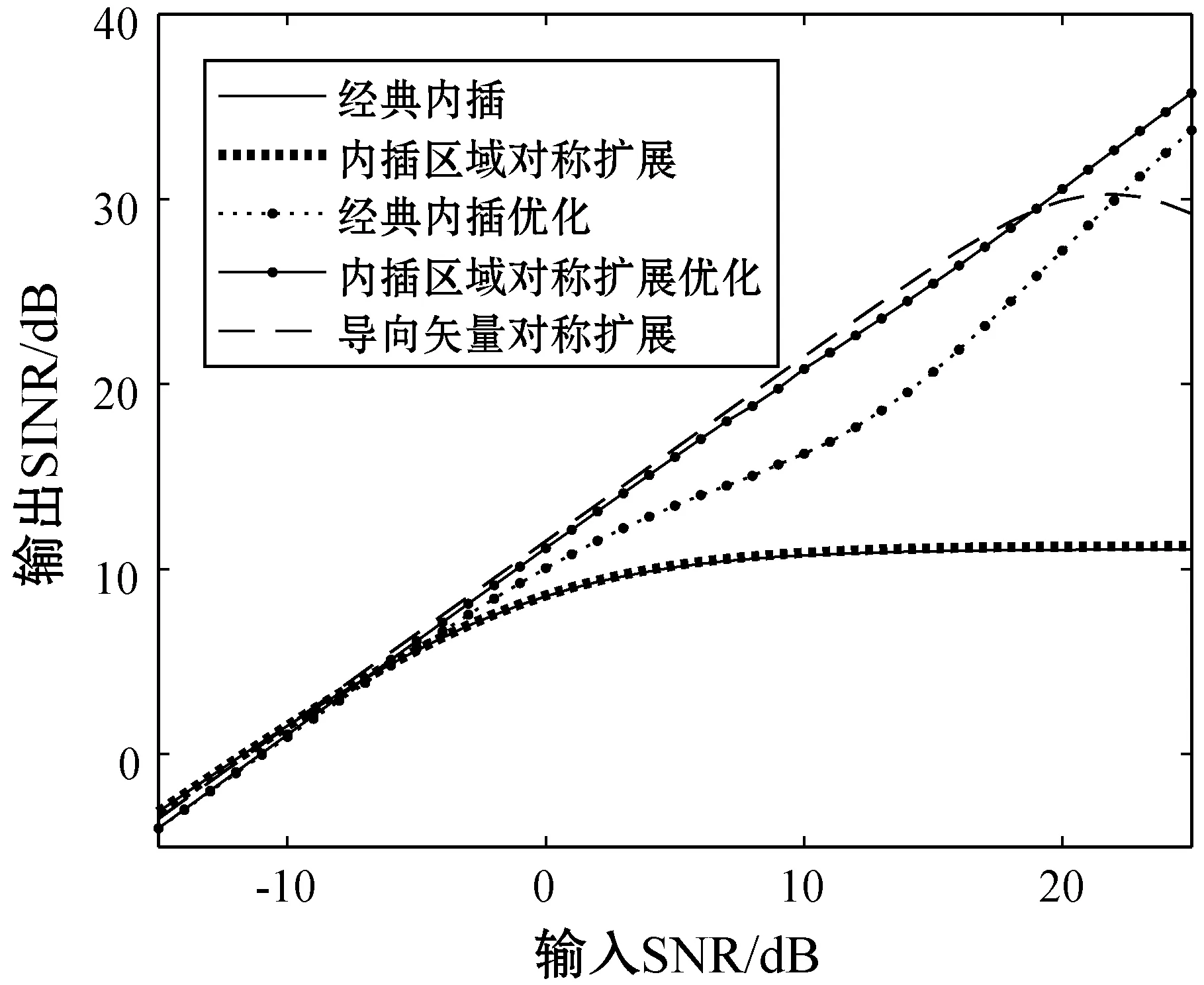
图9 输出SINR随输入SNR变化曲线
可以看出,内插区域对称扩展与经典内插及二者优化的输出SINR均随输入SNR的增加而增加;导向矢量对称扩展的输出SINR呈先增大后减小的趋势,当输入SNR达到21 dB时,其输出SINR开始下降。与经典内插相比,内插区域对称扩展的输出SINR略大,且优化输出的SINR更大,优化效果更明显;与导向矢量对称扩展对比,本文内插区域对称扩展优化的输出SINR始终呈增大趋势,未出现衰减,更适用于高输入SNR。
4 结 语
本文提出一种内插区域对称扩展优化的波束形成算法,实现了内插区域的对称扩展,和经典内插变换相比,一定程度上降低了内插变换的误差,扩大了虚拟扩展阵列的可用内插区域,改善了内插变换过程中的角度敏感问题。在波束形成上,相较经典内插及其优化,本文算法对旁瓣和零陷的抑制较好;相较导向矢量对称扩展,本文算法的旁瓣约束更好。在输出SINR上,相较经典内插及其优化,本文算法具有更高的输出SINR;相较导向矢量对称扩展算法,本文算法的输出SINR无衰减,更为稳定。

