均匀流中声学速度预测的时域解析公式

刘秋洪，王垿桁，薛丝丹，何嘉华

(西北工业大学 翼型叶栅空气动力学重点实验室，西安 710072)

0 引言

经典声比拟理论建立了声场与不同类型声源之间的响应关系，成为工程中应用最广泛的气动噪声数值预测方法。声比拟方法先采用高精度数值方法计算有限域内气动声源信息，然后利用声比拟积分方程模拟噪声传播。FW-H 方程[1]及其扩展形式[2,3]采用封闭可渗透面作为积分面，完整解由面积分和体积分两部分组成。当主要气动声源包围在可渗透面内时，可忽略体积分对声场的贡献[4]，从而仅利用可渗透面上厚度源和载荷源信息外推积分面外声场，比如解析公式F1A[5]和F1C[3]。然而，经典声比拟理论仅关注声压等标量场的预测，没有对声学速度矢量（声波扰动引起的介质粒子振动速度矢量，与声速是两个不同的概念）的外推做出规定，因而是不完整的[6]。声学标量仅表征声波的传播状态，不能清晰阐述声波的能量输运。声强矢量是声压和声学速度的函数，表示单位时间内通过单位面积的噪声能量通量，其方向就是噪声能量的输运方向。声强场的可视化可以详细显示噪声能量的传播路径，有助于揭示声能量辐射机制，Mao 等[7]利用声强可视化说明了旋转声源输出声能的三种模式。噪声传播路径上的非紧致结构会导致声散射，从而改变声场大小、波形和指向性。尽管声散射概念在实际应用中有许多变化[8-9]，但都需要预测散射边界处的声学速度作为边界条件。噪声传播路径分析还有助于噪声抑制方案的研究，Lee 等[10]揭示了散射面对声能再分布的影响，Mao 等[11]研究了阻抗边界的主要吸声位置。

根据线化欧拉方程，采用声压梯度可间接表示声学速度。对静止的声传播介质，Farassat 等[12]提出了一个半解析公式来计算声压梯度。Lee 等[13]导出了用于压力梯度计算的时域公式G1 和G1A，结合等效源法评估了旋翼噪声的声散射[14]。为考虑均匀流的对流效应，Ghorbaniasl 等[15]建立了一个频域声压梯度解析公式，Bi 等[16]则发展了时域声压梯度计算公式G1-M 和G1A-M。声压梯度积分解析公式的提出推动了声比拟方法向矢量场领域拓展。但这些公式在数学表达上都很复杂，且计算量大。

提高声场预测效率对解决气动声学实际问题非常重要。对运动介质中的声传播，声压梯度不能直接表示声学速度，因此需要发展更简明、高效和可矢量化的声学公式。Ghorbaniasl 等[17]基于FW-H 方程提出了声学速度时域计算公式V1 和V1A。Mao 等[18]将公式V1A 推广到频域，得到了公式FV1A 和FV2A，用于计算角速度不变的旋转单极子和偶极子声源诱导的声学速度。Mao 等进一步利用这些声学速度公式分析了简谐点源的声强[7]和声散射[19]。恰如Lee 等[20]指出的那样，声学速度公式V1 和V1A 可以直接从声压梯度公式G1 和G1A 导出。基于声学介质静止假设，Mao 等[21]提出了以声学速度为变量的矢量波动方程，引入了另一种推导公式V1 和V1A 的方法。质量和动量守恒方程在形式上类似真空电动力学的控制方程—麦克斯韦方程，可通过定义“流体电场”和“流体磁场”转换为“流体麦克斯韦方程”[22]。Dunn[6]将电磁类比概念应用于声比拟理论，建立了同时包含声压标量和声学速度矢量（三个分量）的四维声比拟表述，但声学速度的可渗透面源项处理不正确，且没有考虑运动介质的对流效应。

为考虑均匀流对流效应，Mao 等[23]发展了一个对流矢量波动方程，并提出了相应的声学速度半解析公式，本文将其命名为公式V1-M。当均匀流速度为零时，公式V1-M 退化为公式V1。然而对均匀流中的偶极子点源声辐射，半解析公式V1-M 并不能得到正确的预测结果。他们将数值结果的错误归结为偶极子会诱导涡波扰动，使得线化欧拉方程不能描述声学速度。事实上，均匀流中偶极子点源的声辐射是纯声学问题，不会诱发涡波扰动。

本文研究目的是通过分析对流矢量波动方程的右端源项，阐明半解析公式V1-M 的理论不足，提出修正的声学速度积分解析公式CV1A-M，并利用均匀流中单极子和偶极子点源声辐射的理论解验证公式CV1A-M 的正确性。

1 声学速度解析公式V1A-M

假设无穷远均匀来流的密度、压力和速度矢量分别为 ρ∞、p∞和u∞，将当地流动分解为均匀来流和非稳态扰动两部分：

可渗透面f=0 的运动速度为v，且可渗透面单位外法线矢量n=∇f。那么，可渗透面外f＞0区域的连续方程和动量方程可写为：

其 中，H(·)和 δ(·)分别表示Heaviside 函数和Dirac delta 函数，c∞是均匀运动介质中的声速，物质导数符号 D∞/Dt、Lighthill 应力张量Tij以及参数Li和Q分别定义为：

式（5）和式（6）中的 σij和 δij分别表示黏性应力张量和Kronecker delta 函数。

1.1 对流矢量波动方程

从方程（2）和方程（3）出发，文献[23]得到了一个声学矢量波动方程：

其中t*为积分变量。对线性小振幅波动，声学密度ρ′远 小于均匀平均来流密度 ρ∞，因此在可渗透面外存在近似关系 ρu′≈ρ∞u′。Mao 等[23]认为方程（8）右端最后一项的积分核函数为有旋矢量，对声学速度场没有实际贡献，因而将其忽略，从而将声学控制方程最终表述为：

方程（9）的左端是以声学速度为变量的标准对流波动算子，右端七项为声源项，其中第一项为单极子厚度源，紧接着的三项为偶极子载荷源，最后三项为四极子体积源。

1.2 声学速度公式V1A-M

方程（9）的求解可采用对流格林函数，以便考虑均匀流的对流作用。假设均匀流亚声速运动，时域对流格林函数表达式为[2-3]：

其中，g为延迟时间函数，x和t表示观察点的位置与时间，y和 τ表示声源的位置与时间，声学半径 ℜ和R定义为：

式中，M∞=u∞/c∞为均匀来流马赫数，α为均匀来流的对流放大系数，r表示声源y与观察点x之间的距离，即：

如果诱发声辐射的主要气动声源位于可渗透面以内，忽略体积源贡献不会引起明显数值误差，从而可渗透面外的声场可仅根据积分面上的厚度源和载荷源来预测，以提高数值计算效率。根据Farassat 方法[3,5]，文献[23]提出了一个声学速度半解析公式，其中来自厚度源贡献的厚度噪声u′T为：

MR代表声源向观察者方向的运动马赫数：

来自载荷源贡献的载荷噪声u′L为：

a1～a4用于简化积分公式书写，具体表述如下：

方程（14）和方程（18）需要对面积分结果求观察点的时间导数，将其转化为积分符号内对声源的时间导数可以提高计算精度。此外，对可渗透面固定不动的特殊情况，如CAA/CFD 计算或风洞声学问题，参数 ℜ和R、可渗透面外法向矢量n和 声源运动速度v（等于零）是恒定的，不依赖延迟时间，且延迟时间可以采用显式方法得到。对静止可渗透面，本文将方程（14）和方程（18）改写为：

2 声学速度解析公式CV1A-M

文献[23]利用公式V1-M 对均匀流中的单极子和偶极子声辐射进行研究，结果显示单极子声学速度预测结果满足线化欧拉方程，而偶极子声学速度的数值解不满足线化欧拉方程。鉴于方程（14）和方程（18）的推导是正确的，那么对流波动方程（9）的右端载荷源必然会丢失。利用对流格林函数对丢失的载荷面源积分，即可实现对公式V1A-M 的修正。

2.1 对流矢量波动方程源项分析

方程（9）忽略了方程（8）右端最后一项。令

那么根据矢量恒等关系，有：

其中矢量F=n×(ρu′)。显然，对小振幅扰动有近似关系∇×(ρu′)≈ρ∞∇×u′，因此对纯声学问题，式（24）右端第一项近似为零，可被忽略；但第二项为对声场有实际贡献的载荷面源，当平均流速度不为零时不能舍弃。利用式（24），将对流矢量波动方程（9）修正为：

2.2 声学速度公式CV1A-M

SA中 载荷面源的贡献用表示，积分结果可写为：

其中Ei j=εijmFm，εi jm为置换算子。利用关系式：

方程（26）的积分结果为：

对静止可渗透面，方程（30）可进一步表达为：

3 点源算例数值验证

点源声辐射算例常用于气动声学理论公式的数值验证。考虑自激频率 ω=340 rad/s的简谐单极子和偶极子点源声辐射，密度 ρ∞=1.2 kg/m3的均匀流沿x1轴 正向运动，马赫数为0.5，声速c∞=340 m/s。为保持对声学速度公式的关注，并避免与流动模拟准确性有关的任何偏差，可渗透面上的瞬态流动参数，包括压力、密度和速度，都由点源产生的流场精确解产生。声学速度公式中的时间导数采用二阶有限差分方法近似，观察点声学信号采用行进时间算法[24]计算。根据文献[17,23]，取t0=0。

3.1 均匀流中的静止单极子

均匀流中的静止单极子声场可以用一个简单的谐波速度势函数来描述：

其中参数 ℜ和R分别由式（11）和式（12）定义。点源诱导的声学速度、压力和密度场为：

单极子位于坐标系原点，速度势函数的幅值为A=1 m2/s。采用中心在坐标系原点且半径为0.5 m的球面作为可渗透积分面，并利用数量为7 840 的四边形网格离散积分面，确保空间解析精度。在每个声源周期T内布置128 个时间步，保证差分算法的数值精度。36 个观察点均匀布置在x1-x2平面内半径为10 m 的圆上，将基于x1轴测量到的观察点与坐标原点间的几何角度定义为观察角θ。

所有观察点的时间步长与声源时间步长保持一致，输出一个声源周期（128 个时间步）的声学信号。将观察角 θ=120°处声学速度分量的时间历程预测值与理论解进行对比，结果如图1 所示。公式V1A-M 的数值解接近理论值，但在波峰与波谷附近仍存在一定差异；公式CV1A-M 的数值解则与理论值一致。

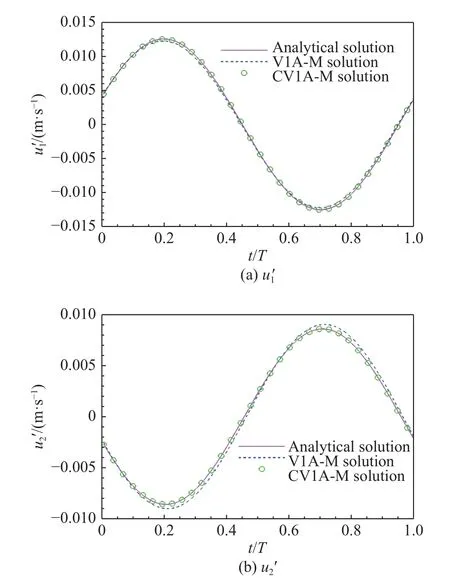
图1 θ=120°静止单极子声学速度时间历程Fig.1 Acoustic velocity time histories of a stationary monopole at θ=120°

图2 不同观察点处静止单极子声学速度均方根值Fig.2 RMS value of the acoustic velocity of a stationary monopole at different observation points

3.2 均匀流中的静止偶极子

考虑均匀流中静止偶极子的声辐射，假设偶极子的轴线与x2轴对齐，速度势函数可表示为：

偶极子的位置、自激频率、速度势函数幅值、可渗透面网格，以及观察点的设置，均与单极子点源算例相同。诱导的声学速度、压力和密度场理论解分别采用式（34）、式（35）和式（36）计算。

图3 为1 20°观察点声学速度数值解随时间的变化历程及其与理论解的对比。由于可渗透面有效声源部分丢失，公式V1A-M 预测的声学速度分量和与理论解存在显著差异；修正后的公式CV1A-M 能获得与理论解一致的数值结果。改变平均流的速度（包括大小与方向）、点源的自激频率或可渗透面的大小，公式CV1A-M 均能得到与理论解完全吻合的结果（这里不再给出）。图4 为不同观察点处偶极子声学速度分量均方根值数值解与理论解的对比。公式CV1A-M 数值解再一次与理论值保持一致，而公式V1A-M 数值解在点源上游与理论解存在巨大差异。公式V1A-M 丢失的源项为载荷面源，因而偶极子点源的数值误差远大于单极子算例的数值误差。

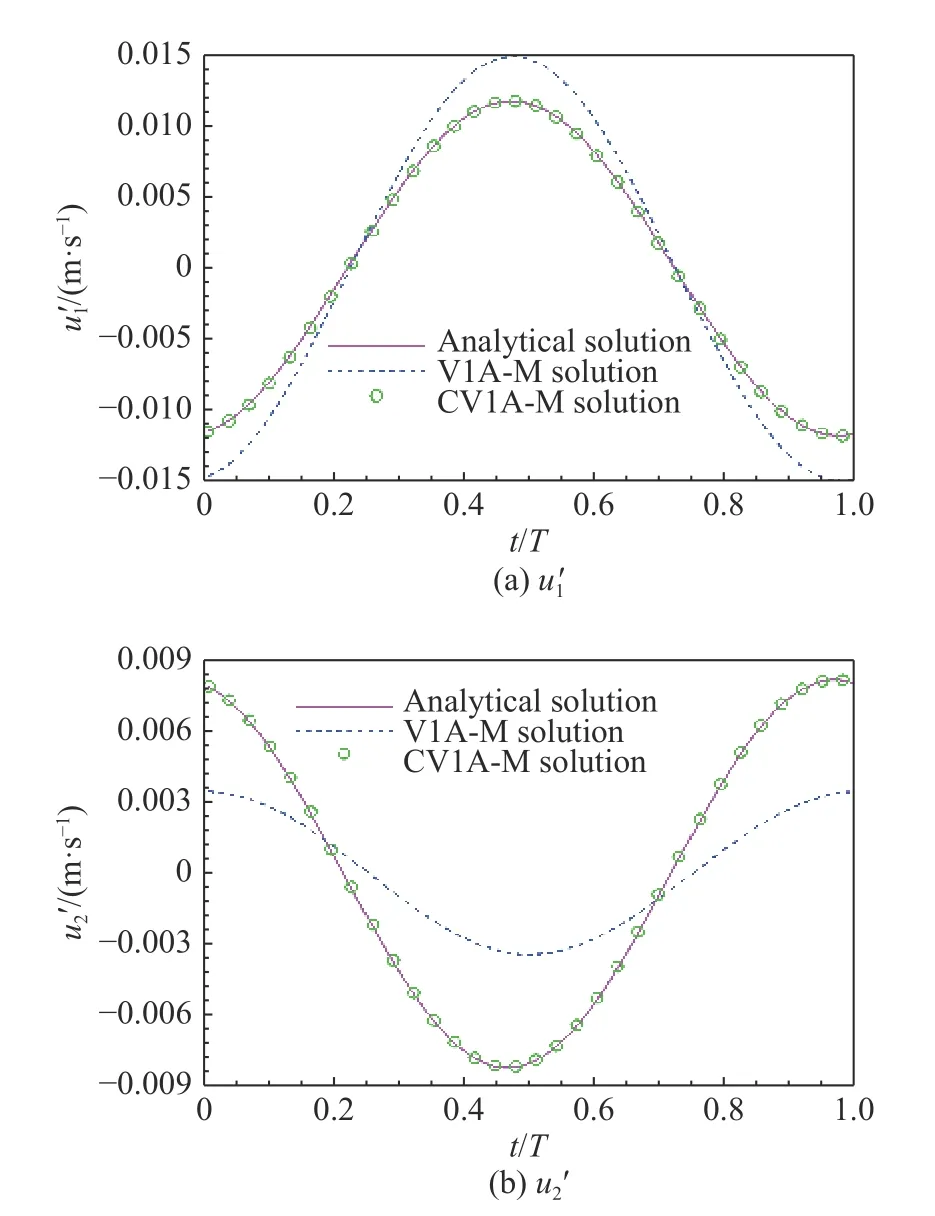
图3 θ=120°静止偶极子声学速度时间历程Fig.3 Acoustic velocity time histories of a stationary dipole at θ=120°

图4 不同观察点处静止偶极子声学速度均方根值Fig.4 RMS value of the acoustic velocity of a stationary dipole at different observation points

3.3 均匀流中的旋转单极子

对运动点源算例，假设初始方位角为 0°的点源以恒定角速度 Ω=ω/4绕x3轴逆时针旋转，旋转半径d=0.25 m，如图5 所示。点源自激频率、速度势函数幅值、可渗透面网格和观察点位置均与静止点源算例相同，输出512 个时间步（对应4 个声源周期）的声学速度信号。

图5 均匀平均流中旋转点源示意图Fig.5 The schematic of a rotating point source in a uniform mean flow

运动单极子点源的速度势函数为：

其中MR为延迟时刻点源向观察点方向运动的马赫数，由式（17）定义。图6 为1 50°观察点声学速度时间历程的数值解与理论解对比。公式V1A-M 预测的声学速度分量与 理论值基本吻合，而与理论值存在大小和相位上的明显差异。公式CV1A-M 的数值解与理论解的一致性进一步验证了其正确性。

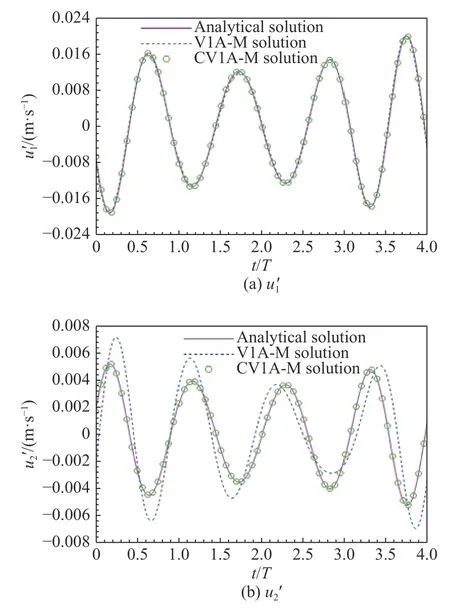
图6 θ=150°旋转单极子声学速度时间历程Fig.6 Acoustic velocity time histories of a rotating monopole at θ=150°

图7 对比了不同观察点处旋转单极子声学速度分量均方根值的数值解与理论解。公式CV1A-M 的数值解与理论值是一致的，公式V1A-M 的数值解在点源上游方向，尤其是1 80°观察角附近，与理论值差异明显。

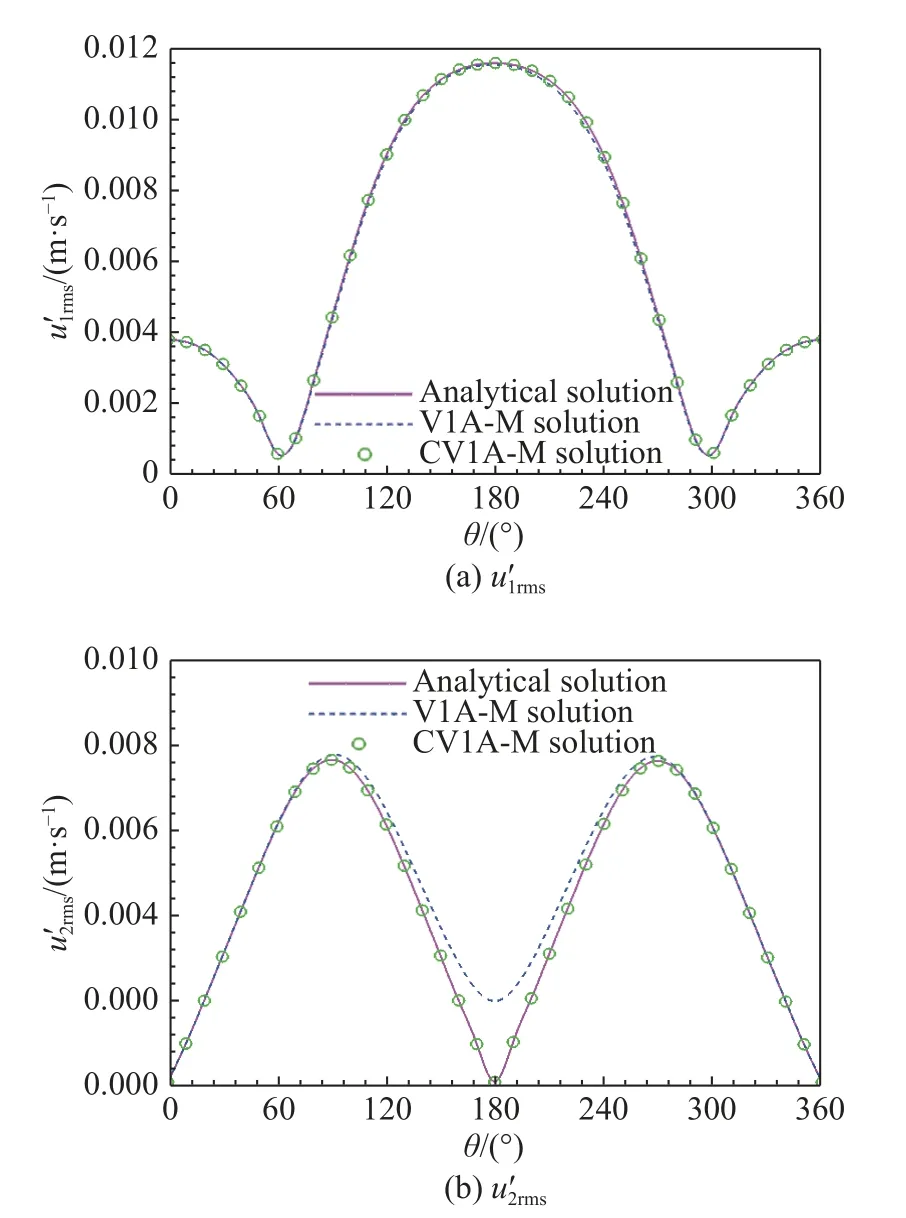
图7 不同观察点处旋转单极子声学速度均方根值Fig.7 RMS value of the acoustic velocity of a rotating monopole at different observation points

3.4 均匀流中的旋转偶极子

仍然假设运动偶极子点源的轴线与x2轴对齐，速度势函数可根据旋转单极子的势函数得到：

图8 为1 50°观察点旋转偶极子声学速度时间历程的数值解与理论解对比。公式CV1A-M 的数值解与理论解一致；声学速度分量的公式V1A-M 数值解虽然大小与理论值不吻合，但相位相同，而分量的公式V1A-M 数值解大小和相位与理论值均存在巨大差异。图9 比较了不同观察点处旋转偶极子声学速度分量均方根值的数值解与理论解。公式CV1A-M数值解与理论值一致，公式V1A-M 数值解在点源上游与理论解差异巨大。这是意料之中的结果。

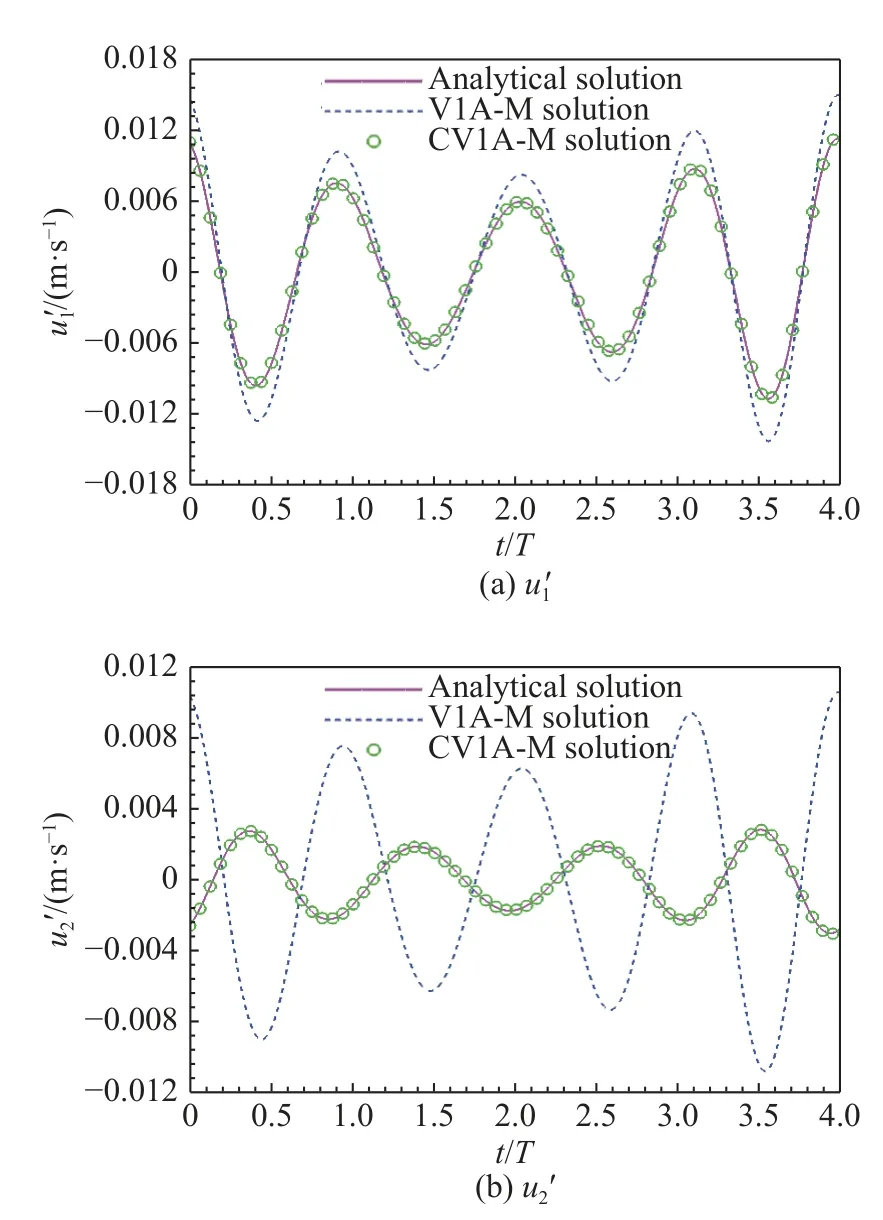
图8 θ=150°旋转偶极子声学速度时间历程Fig.8 Acoustic velocity time histories of a rotating dipole at θ=150°

图9 不同观察点处旋转偶极子声学速度均方根值Fig.9 RMS value of the acoustic velocity of a rotating dipole at different observation points

均匀流中点源声辐射诱导的声压计算公式（35）是根据线化欧拉方程和声学速度计算公式（34）得到的，因此对纯声学问题，声学速度和声学压力满足线化欧拉方程。在上述4 个典型算例中，声学速度公式CV1A-M 的数值解均与理论值一致，证明了该公式的理论正确性。公式V1A-M 不能实现均匀流中偶极子声学速度的预测，并非线化欧拉方程不能描述偶极子声学速度，而是可渗透载荷源部分丢失引起的。

4 结论

文献[23]提出的对流矢量波动方程丢失了部分对声场有贡献的可渗透面载荷源，使得公式V1-M 和V1A-M 难以准确外推声学速度，即便对单极子算例，数值解与理论值仍存在明显误差；受均匀流对流作用影响，点源上游方向的公式V1A-M 数值解误差远大于下游方向误差。

通过考虑被丢失的可渗透载荷源贡献，发展了积分解析公式CV1A-M。对均匀流中静止或旋转单极子和偶极子而言，公式CV1A-M 的数值解与理论值一致。均匀流中的偶极子点源声辐射不会诱发涡波扰动，线化欧拉方程可以准确描述偶极子诱导的声学速度与声学压力间的关系。

对真实的流动诱发气动噪声问题，可渗透面往往穿过一定的非线性区域。尽管主要的气动声源被可渗透面包围，但当涡波通过可渗透面时，涡波扰动会被收集为积分面的输入而产生伪声。声学速度公式CV1A-M 的实际应用还需发展相应的伪声抑制方法，这是未来需要关注的研究方向。