面对称无尾高超声速飞行器三通道耦合失稳判据

吕 达，张维桐，张鲁民，赵俊波，张石玉，苏浩秦

(1.中国航天空气动力技术研究院，北京 100074；2.北京航空航天大学 宇航学院，北京 100191；3.国家计算流体力学实验室，北京 100191)

0 引言

随着打击时敏目标和机动突防的需求日益增长，具备高升阻比、高机动性能的面对称升力式构型已成为高超声速飞行器气动布局主流发展方向。2010 年美国HTV-2、X-51A、X-37B 的试飞[1-4]，标志着继航天飞机以后的新型面对称高超声速飞行技术的工程化成为可能。同时，以进一步提升气动与飞行性能为设计目标的无尾布局是高超声速飞行器未来的重要发展方向。无尾布局外形简洁，具备全向宽频隐身特性好、升阻特性优、气动热载荷低等性能优势，但在通道耦合和考虑耦合的操稳设计方面存在难题，急需技术攻关。主要体现在：对于无尾布局高超声速飞行器，由于不存在垂尾，俯仰、滚转和偏航三个通道的稳定特性只能依赖机体的设计，而机体的形态和几何参数又受容积率、升阻比等指标的约束，稳定性调节范围较小，且其横航向稳定性较差，因此综合多重指标的优化设计难度极大。同时，无尾布局飞行器通常采用欠驱动控制，其通道间耦合效应较强，耦合操稳特性的设计难度较大。因此，发展以三通道判据为核心的精细化耦合稳定性分析思想对于先进的无尾布局高超声速飞行器的设计具有重要意义。

20 世纪50 年代中期以来，科技工作者对飞行器耦合失稳开展了大量研究。文献[5]系统总结了各类判据，如：Moul、Weissman、Kalviste、Johnston、Bihrle、Pelikan 等的研究成果。历经多年发展，如今上述各类判据已经成为航空航天飞行器稳定性分析的重要工具。文献[6]详细总结了飞行器耦合失稳各类判据在现阶段国内外飞行器设计工作中的应用。

近年来，随着无尾布局高超声速飞行器技术的发展，国内外对于耦合稳定性的研究进一步深入。例如，Park 等[7]使用一系列气动分析方法评估了无尾飞行器的稳定性和控制特性，利用纵向和横向运动的系统矩阵推导了无尾飞行器的稳定性准则，对几种飞行条件进行了稳定性分析。Fu 等[8-10]提出了一种飞行试验，用以研究具备荷兰横滚模式稳定性但不具备偏航稳定性的飞行器的耦合稳定特性。Shen[11-12]为了准确预测偏离行为，在控制系统的设计过程中考虑偏航-滚转耦合的影响，并进行了不同耦合比下的偏航-滚转耦合风洞试验。此外，还有许多文献在飞行器气动设计[13-16]和飞行器控制系统设计[17-23]的过程中考虑了耦合稳定性偏离特性的影响。

本文通过理论推导以及数值仿真试验，引入了开环及闭环情况下的3 个静稳定性耦合判据和3 个动稳定性耦合判据。与传统的判据相比，更为全面地考虑了飞行器三通道耦合对其稳定性的影响，可用于精细化地分析近代先进无尾布局高超声速飞行器三通道的耦合稳定特性，且对其设计过程具有指导意义。

1 飞行器的姿态动力学方程组

利用刚体假设建立飞行器的六自由度动力学模型，忽略地球自转的影响，根据动量、动量矩定理，可以导出飞行器机体坐标系下的六自由度动力学方程组[24]。

飞行器运动可分解为平动和转动，而确保转动运动稳定性是保证飞行器飞行稳定性的最根本条件。根据飞行器的六自由度动力学方程组，忽略平动速度影响，可得：

同时，对于角加速度方程组，由小扰动线性化方法，可得到角加速度方程组：

飞机相对于速度矢量的方向可由3 个角度定义，其中两个分别为攻角和侧滑角 (α,β)，现增加侧倾角µ。与体轴系滚转角绕体轴ox转动的定义不同，侧倾角 µ定义的是飞行器的升力矢量相对于速度矢量的旋转角度，具体见文献[24]，侧倾角速率与体坐标系中角速率的关系为：

略去位移运动的影响，略去惯性积，由小扰动线性化方法，得到简化的飞行器姿态动力学方程组为：

式中的算子定义如下：

2 开环三通道静动稳定性耦合判据

2.1 俯仰静动稳定性耦合判据

利用小扰动线性化方法，选择式（4）中第一个方程和式（5）组成俯仰通道系统的线化动力学模型：

对于该类飞行器，其横航向阻尼较小，仅考虑由俯仰通道 Δα和 Δq产生的耦合力矩，忽略式（7）中的滚转和偏航阻尼项，可得简化的系统矩阵如下：

则其特征方程为：

由于忽略了横航向的阻尼，故特征方程失去了一个根，则分别由劳斯判据的c＞0 和bc-ad＞0，有俯仰静稳定性开环耦合判据和俯仰动稳定性开环耦合判据：

进一步得其无量纲的形式为：

2.2 偏航静动稳定性耦合判据

选择式（4）中第二个方程以及式（5）组成偏航通道系统的线化动力学模型：

仅考虑由偏航通道 Δβ 和 Δr产生的耦合力矩，故忽略式（12）中的滚转阻尼项，保留俯仰阻尼系数，可得偏航通道简化的系统矩阵如下：

其特征方程为：

分别由劳斯判据的c＞0 和bc-ad＞0，从而有偏航静稳定性开环耦合判据和偏航动稳定性开环耦合判据：

无量纲化得到下式，式中Q为动压，S为参考面积，l为参考长度。

2.3 滚转静动稳定性耦合判据

选择式（4）中第三个方程以及式（5）组成滚转通道系统的线化动力学模型。此时由于后三个方程不显式地含有μ，但μ变化时会同时引起β的变化，μ对力矩的影响可以通过力矩对于β的导数来体现，故应寻找在滚转通道运动下μ和β的近似关系。

由于面对称的无尾布局高超声速飞行器的侧滑角通常希望被控制在0°，图1 为当β接近于0°时由于飞行器滚转运动带来的β及μ变化的近似关系。图中OAC平面为飞行器受扰前的对称面，OAB为受扰后的对称面，OXs为受扰后的稳定轴系的X轴，A为体轴系上一点，AB为过点A向OXs轴做的垂线，AC为过点A向风轴系X轴做的垂线，由于OXs为稳定轴系的X轴，故OAB平面与OBC平面垂直，且AB垂直于OXs，故AB垂直于OBC平面，从而AB垂直于OC，又由于AC垂直于OC，且AB和AC又分别在飞行器受扰后与受扰前的对称面中，故AB和AC可以认为是飞行器的升力方向，则根据侧倾角的定义，AB和AC之间的夹角即为侧倾角μ，故由图中几何关系有：

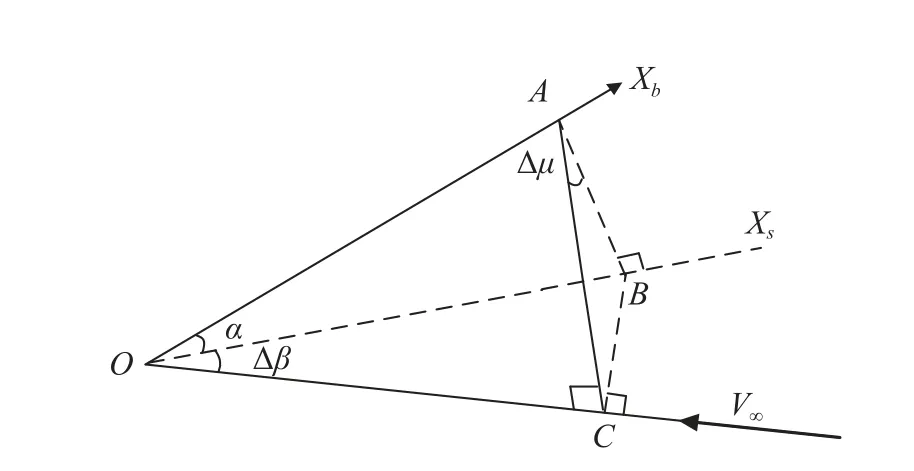
图1 当β 接近于0 时由于滚转通道运动带来的β 及μ 变化的近似关系Fig.1 Approximate relationship between variations of β and μ due to roll channel motion when β is close to 0

即当研究飞行器的滚转通道运动时，有如下近似关系：

式（19）即μ的力矩系数的近似表达，注意，μ的力矩系数在实际中并不存在，本文只是利用了飞行器滚转运动时μ和β的近似关系导出了由于μ的变化而造成了β的伴随变化而导致的力矩改变。

则滚转通道系统的线化动力学模型近似为：

与其他两通道类似，仅考虑由滚转通道 Δµ和Δp产生的耦合力矩，忽略式（20）中的偏航阻尼项，保留俯仰阻尼系数，可得简化的系统矩阵如下：

分别由劳斯判据的c＞0 和bc-ad＞0，有滚转静稳定性开环耦合判据和滚转动稳定性开环耦合判据：

其无量纲简化的形式如下：

2.4 本文判据与现有判据的对比阐释

与传统的气动稳定性判据相比，本文判据在攻角为正，且攻角和侧滑角接近于零时，可退化为前者，即ClβDYN=Clβ，CmαDYN=Cmα，CnβDYN=Cnβ。此外，若忽略本文判据中气动力矩系数的小量，则本文判据同样可退化为传统判据。与传统判据的临界值皆为0 不同，由于本文考虑了俯仰通道动导数对横航向的影响，故横航向判据的临界值不为0。因此，本文所述判据与传统的气动稳定性判据仍然有着不可分割的联系，本文所述判据是现有判据的进一步完善，对于稳定性可调节范围较小的无尾布局高速飞行器的气动稳定性设计具有指导意义。

3 闭环三通道静动稳定性耦合判据

3.1 俯仰闭环静动稳定性耦合判据

采用升降舵作为俯仰通道控制力来源。考虑攻角及俯仰角速度镇定，利用攻角及俯仰角速度反馈至升降舵的方式，反馈控制律采用以下形式：

式中 δe为升降舵的舵偏角，则有闭环的俯仰系统矩阵为：

由劳斯判据c＞0，有俯仰通道闭环静稳定性耦合判据为：

3.2 偏航闭环静动稳定性耦合判据

采用副翼作为偏航方向控制力来源。考虑镇定侧滑角及偏航角速度，即实施侧滑角及偏航角速度反馈至副翼，反馈控制律采用以下形式：

式中，δa为副翼的差动偏角，忽略副翼引起的侧向力以及俯仰力矩的变化，则有闭环的偏航系统矩阵为：

则其闭环特征方程为：

由劳斯判据c＞0，有偏航通道闭环静稳定性耦合判据为：

3.3 滚转闭环静动稳定性耦合判据

同样采用副翼作为滚转通道控制力来源。考虑镇定侧倾角μ及滚转角速度p，即实施侧倾角及滚转角速度反馈至副翼 δa，反馈控制律采用以下形式：

式中，δa为副翼的差动偏角，忽略副翼引起的俯仰力矩的变化，则有闭环的滚转系统矩阵为：

由劳斯判据c＞0，有滚转静稳定性闭环耦合判据：

其无量纲简化的形式为：

4 三通道稳定性耦合判据数值仿真验证

本节通过一个数值仿真案例来验证所提出的三通道稳定性耦合判据的有效性。采用某型面对称无尾布局高超声速飞行器作为研究对象[15]，其基础外形1 如图2 所示，将基础外形的前缘后掠角增大，且将飞行器底部截面高度增加，侧缘切削量增大，得到外形 2；将基础外形的前缘后掠角减小，并将飞行器底部截面高度增加，且将其质心适当向后调整，得到外形3；最后将基础外形的前缘后掠角减小并适当飞行器底部截面高度，得到外形 4。

图2 基础外形的三视图[15]Fig.2 Three views of basic configuration[15]

首先选取基础外形1，对其气动稳定性进行评估。图3 为计算域以及对称面的网格划分，采用结构网格，壁面第一层网格高度设置为0.001 mm，以保证y+值小于1。采用基于三维积分形式的雷诺平均N-S方程求解，湍流模型采用S-A 模型，无黏通量采用差分分裂的Roe 格式，黏性项采用二阶中心差分格式进行离散，时间推进格式采用隐式近似因子分解法。选取类似外形的少量试验数据对该计算方法进行验证，风洞试验模型如图4[25]所示，采用该方法得到的结果与试验得到的结果对比如图5，可见两者结果在量值及趋势上吻合较好。其他三种外形类似，不再赘述。

图4 风洞试验模型[25]Fig.4 Wind tunnel test model[25]

图5 数值计算及风洞试验结果对比Fig.5 Comparison of CFD and experimental results

利用CFD 计算得到的气动数据进行六自由度动力学仿真。对于基础外形1，其在攻角2°时由CFD 仿真得到的核心气动稳定性数据以及其他三种外形的核心气动稳定性数据如表1 所示。为了方便判断其偏离特性，仿真的判据临界值近似取0，可见外形1 不同时满足三通道稳定性耦合判据，由于没有垂尾，导致CnβDYN＜0，偏航通道不稳定，且ClβDYN的绝对值偏小，即滚转通道稳定性偏小。取初始配平状态：α0=2°，β0=0°，µ0=0°，p0=0(°)/s，q0=0(°)/s，r0=0(°)/s，假设飞行器的滚转角速度在仿真初始时刻受到扰动变为p=p0+Δp=1(°)/s，则可得侧倾角、攻角和侧滑角以及姿态角速度的变化曲线如图6 和图7 所示。由图可得，飞行器的侧滑角以及侧倾角迅速发散，攻角在一段时间之后也发散，飞行器处于不稳定状态。

表1 本文仿真涉及到的4 种外形在攻角2°时的核心气动稳定性数据Table 1 Core aerodynamic data at 2° angle of attack of the four configurations involved in the simulation

图6 飞行器的姿态角速度的变化曲线Fig.6 Variation of aircraft angular velocity

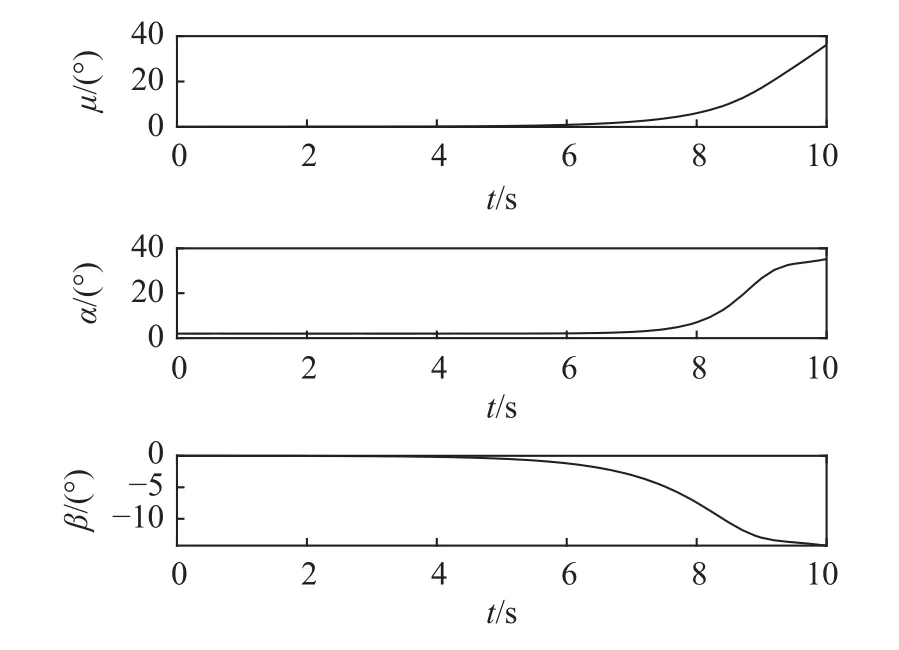
图7 飞行器的侧倾角、攻角和侧滑角的变化曲线Fig.7 Variations of aircraft roll angle,angle of attack,and sideslip angle

对于外形2，使其在同样的初始攻角情况下满足CnβDYN＞0，CmαDYN＜0，但ClβDYN＞0，如表1 所示，即滚转通道不稳定，偏航通道弱稳定，给定初始状态α0=2°，β0=0°，µ0=0°，p0=0(°)/s，q0=0(°)/s，r0=0(°)/s，在仿真初始时刻给相同的滚转角速度扰动Δp=1(°)/s，仿真结果如图8 和图9所示。由图可得，飞行器侧倾角迅速发散，且由于耦合效应，攻角以及侧滑角随后也发散，飞行器处于不稳定状态。

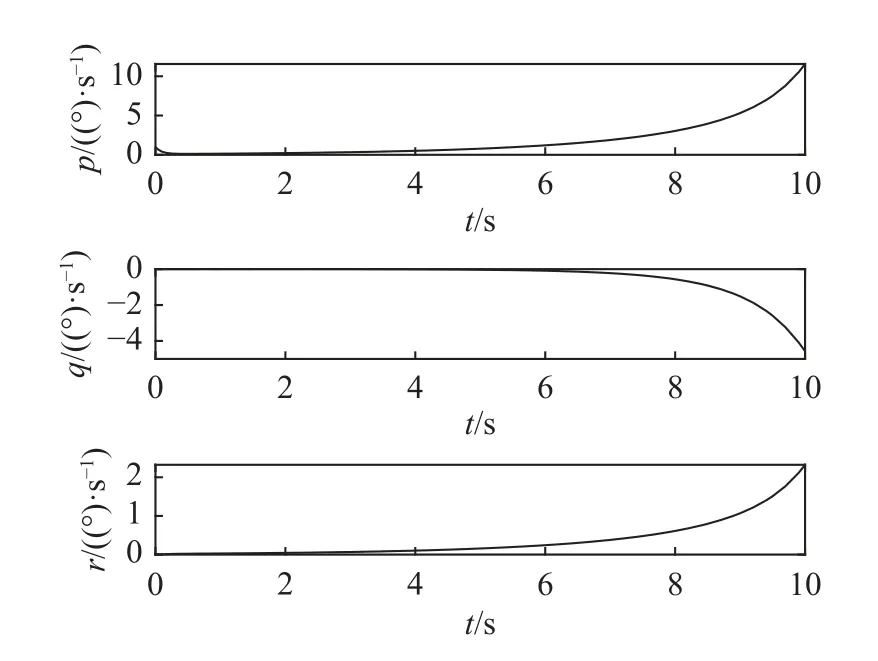
图8 飞行器的姿态角速度的变化曲线Fig.8 Variation of aircraft angular velocity

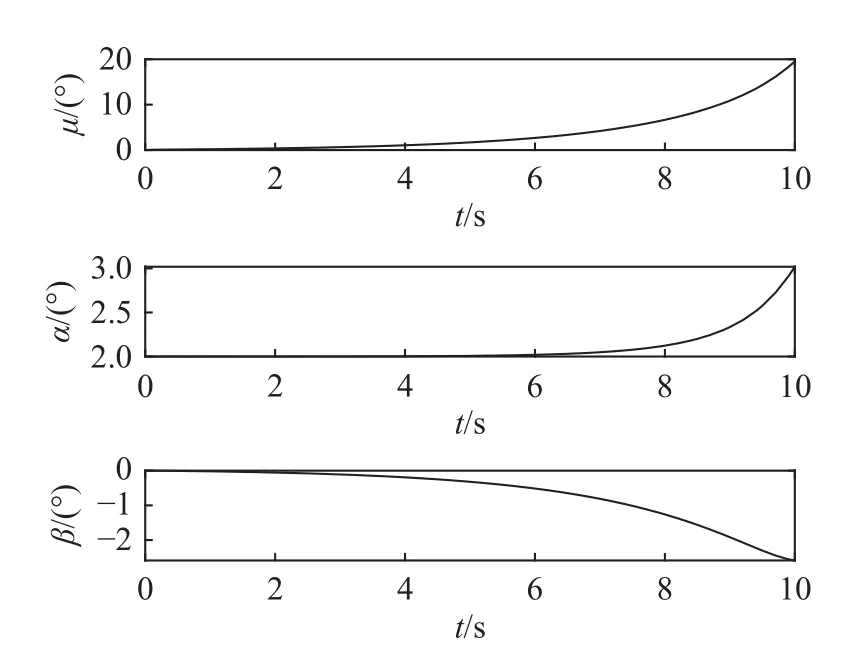
图9 飞行器的侧倾角、攻角和侧滑角的变化曲线Fig.9 Variations of aircraft roll angle,angle of attack,and sideslip angle

对于外形3，使其在同样的初始攻角情况下满足CnβDYN＞0、ClβDYN＜0，但CmαDYN＞0，如表1 所示，即俯仰通道不稳定，滚转和偏航通道弱稳定，给定初始状态α0=2°，β0=0°，µ0=0°，p0=0(°)/s，q0=0(°)/s，r0=0(°)/s，仿真初始时刻给定相同的扰动 Δp=1(°)/s，仿真结果如图10 和图11 所示。由图可得，飞行器攻角迅速发散，且由于耦合效应，侧倾角以及侧滑角随后发散，飞行器处于不稳定状态。

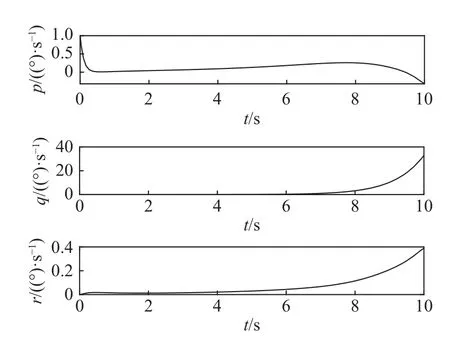
图10 飞行器的姿态角速度的变化曲线Fig.10 Variation of aircraft angular velocity

图11 飞行器的侧倾角、攻角和侧滑角的变化曲线Fig.11 Variations of aircraft roll angle,angle of attack,and sideslip angle

对于外形4，使其在同样的初始攻角情况下满足CmαDYN＜0、ClβDYN＜0，CnβDYN＞0，如表1 所示，即满足三通道的稳定性耦合判据。给定初始状态α0=2°，β0=0°，µ0=0°，p0=0(°)/s，q0=0(°)/s，r0=0(°)/s，同样在仿真初始时刻施加相同的扰动 Δp=1(°)/s，仿真结果如图12 和图13 所示。由图可得，飞行器侧倾角、攻角以及侧滑角均收敛到稳定的值，飞行器处于稳定状态。

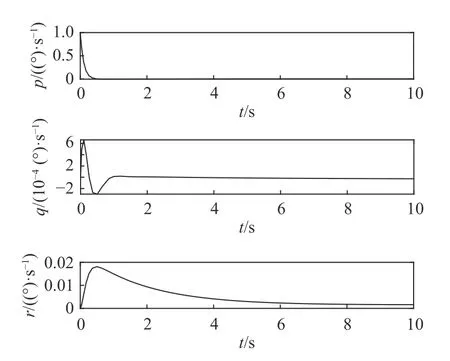
图12 飞行器的姿态角速度的变化曲线Fig.12 Variation of aircraft angular velocity

图13 飞行器的侧倾角、攻角和侧滑角的变化曲线Fig.13 Variations of aircraft roll angle,angle of attack,and sideslip angle

综上所述，当无尾布局高超声速飞行器同时满足本文所提出的三通道稳定性耦合判据时，飞行器处于稳定状态。反之，则会出现各种耦合失稳问题。初步说明本文提出的三通道稳定性耦合判据是有效的。

5 结论

针对无尾布局高超声速飞行器飞行中的通道耦合偏离失稳问题，本文推导了面对称无尾布局高超声速飞行器三通道的气动稳定性耦合判据，并通过几组数值仿真算例初步验证了本文判据的有效性，完善了判断此类飞行器静动稳定性的判别方法。与传统判据的临界值皆为0 不同，由于本文考虑了俯仰通道动导数对横航向的影响，故横航向判据的临界值不为0，本文判据相比传统判据考虑的因素更加全面。

本文判据在推导过程中应用了小扰动线化理论且省略了许多因素，因此，该判据仍具有一定局限性，未来需要通过数值仿真、地面试验及飞行试验，进一步验证判据的有效性。同理，对本文建立的闭环稳定性耦合判据也需要通过进一步地研究以验证其可靠性。