偶然与随意——都是必然——以《认识6～9》教学为例谈对教材的理解

文|杨 睿

教师对教材的解读应该是多元的，可以依据《义务教育数学课程标准（2022 年版）》，从把握数学学科本质，立足知识结构，结合具体学情，站在儿童的立场上，基于学生的视角对教材进行深度解读。课堂上发生的偶然和随意，都是基于学生认识水平和对教材的解读而产生的必然。

一、看似偶然，绝非随意

听一年级《认识6～9》一课，学生在认识6～9 之后，为巩固对6～9 的认识，进行及时反馈练习，看数涂色。一个一个地涂6 个圆表示6，一个一个地涂7 个圆表示7……让学生体会6 个一合起来是6，7 里面有7 个一……有些学生在涂色时还能感受到5 个和1 个合起来是6 个，3 个和4 个合起来是7 个……这些都能丰富学生对6～9 各数的体验。汇报交流时，全班同学几乎整齐地涂成了一样的（如下图）。

此时，有学生发表不同想法：竖着涂或涂成红色可以吗？

学生出现竖着涂、用红色涂，看似偶然，实则是学生基于1～5 的认识经验产生的，是学生已有数学经验和对数的概念的认识的必然反应。

针对课堂上的偶然事件，细读教材：

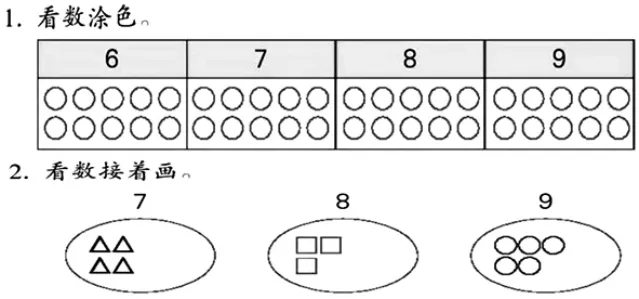
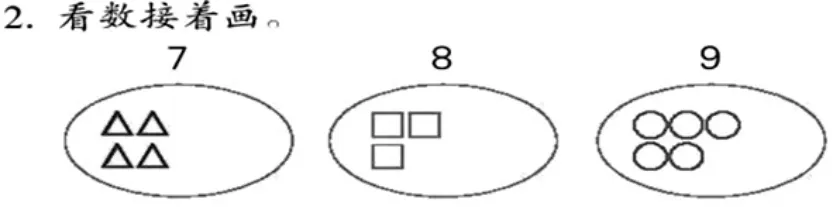
第1 题涂色部分全是○，而第2 题，形状变成了△、□、○，颜色也分别变成了红色、蓝色和绿色。教学时既要兼顾数的认识和组成，还要丰富学生对数的概念的理解。建议可以分三个层次开展：

1.有序思考，感受数的组成

教师质疑：刚才我们认识了6～9，你能涂出6～9吗？快速地涂一涂。

2.方法多样，丰富数的认识

教师质疑：刚才大家都是横着涂的，老师发现一个同学涂得很特别，你有什么想说的？

学生交流：他是竖着涂的，也是6。

再次质疑：横着涂、竖着涂都可以，有了他的启发，你能涂出不一样的6 吗？

……

再次展示：这位同学涂成了红色，还是6 吗？

追问：有了她的启发，你还能涂出不一样的6 吗？

……

3.异中求同，深化数的概念

质疑：刚才同学们有横着涂、竖着涂、隔着涂、涂成黄色的、涂成不同颜色的，为什么它们都可以表示“6”呢？

交流：涂的形状、顺序、颜色和6 没关系，只要有6 个，就表示6。

总结：无论什么形状、什么顺序、什么颜色，只要是6 个，就可以表示6。有了6 的启发，相信大家涂7、8、9 时一定是形状各异、五颜六色的，快速涂一涂你心中的7、8、9 吧。

操作：学生涂出创意的7、8、9

通过这样的操作活动，学生对数的认识就会把形状、顺序、颜色等这些关于“6”的非本质属性剥离出去，留下“6”的本质属性——只要是6 个就可以表示6，丰富学生对数概念的理解。同时也可以更好地体会数的组成：6 还可以分成3 和3，2 和4，1 和5。

挖掘蕴含在操作里的数学思考内容，让学生创新性表达，对建立数概念十分有益。数学概念是数学理论体系的基石,是客观现实中的数量关系与空间形式的本质属性在人脑中的反映。小学生以形象思维为主，而数学概念是抽象的。掌握和理解概念对提高学习效率、培养逻辑思维能力、形成空间观念和抽象概括能力都有着重要意义。同时，在操作活动中渗透了从不同中找相同的数学思考方法。有了练习1 的操作活动，学生在进行练习2 的操作时，就会明白颜色和形状无所谓，是几就画几个。

二、看似随意，绝非偶然

看似简单的练习，少部分学生还是圈成左边5 朵或7 朵，也许我们会归结为粗心，是学生无意注意发生的作用。细读教材，看似随意的错误，实则是练习方法的缺失，学生的错误绝非偶然。题目中含有“左边”“6 朵”两个条件涉及“方向”和“数量”，练习时可以引导学生分为三步走：

1.确定方向

2.确定数量

3.边线成圈

如果操作活动按三步走，学生的错误就会减少，学生的练习技能将有所提升。看似随意的错误，绝非偶然，是对教材的习题没有充分挖掘。

课堂上发生的偶然与随意，都是基于学生认知水平产生的必然。教学中要基于教材、基于学情，这样才能将偶然与随意转化成有效的教学生成，促进学生思维和技能的提升。