等式的基本性质

文|陈 银

在认识数量关系的过程中，理解等式的基本性质是从算术思维转换到代数思维的一个重要转折点。利用猜想、归纳、推理的学习方法，从数学的角度去分析数量之间的关系和规律，在具体情境中运用等式基本性质进行解释说明，提高学生的代数思维，可采用如下教学环节。

一、操作感知，理解平衡

1.表征

出示天平（图1），如果1 个圆柱的质量是3，1 个正方体的质量是1，用算式表示关系。

图1

算式：3=1×3

2.研究：天平还能平衡吗？

操作要求：3 个立体图形，长方体的质量是b，如果天平继续平衡，用等式表示变化过程。（图2）

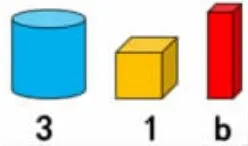
图2

3.比较

（1）两边都加上一个数，所得结果仍为等式。

例如：左右两边再加一个正方体，算式表示为3+1=1×3+1。

（2）两边都加上一个式，所得结果仍为等式。

例如：左右两边再加一个长方体，算式表示为3+b=1×3+b。

通过计算、天平验证等方式，发现天平仍保持平衡，最终得到“等式两边都加上一个数或式，所得结果仍是等式”的结论。

4.验证：再写一些等式来验证结论是否成立。

二、大胆猜测，迁移过程

1.迁移经验，猜测验证

猜想1：等式两边都减去一个数，所得结果仍是等式。

猜想2：等式两边都乘一个数，所得结果仍是等式。

猜想3：等式两边都除以一个数，所得结果仍是等式。

2.研究新的问题

选：选择不同的猜想；变：在算式中表示；写：通过天平或计算探究规律；验：验证规律是否成立。

3.交流汇报，验证猜测

（1）减法的规律。

通过计算、动画演示，发现取出同样的质量，天平仍然平衡，等式仍然成立。

（2）乘法的规律。

天平两边物品的数量分别扩大到原来的3 倍、4 倍、5 倍等，天平仍保持平衡，交流发现等式左边是原来的几倍，等式的右边也是原来的几倍，等式依然成立。学生也进一步理解天平平衡不是取决于放的物品是否相同，而是取决于所放物品的质量是否相同。

（3）除法的规律。

通过除法的意义来帮助理解，例如6=1×6，6÷3=1×6÷3 中发现左边质量平均分成3 份，右边质量也平均分成3 份，天平仍然平衡，只要左右两边同时平均分成相同的份数，最后等式仍然相等。

4.补充规律，完善提升

（1）乘或除以一个数时，需要把0除外。

（2）发现的四个规律分为两类：等式基本性质1：等式两边都加上或减去同一个数或式，所得结果仍为等式；等式基本性质2：等式两边都乘或除以同一个不为0 的数或式，所得结果仍为等式。

三、性质应用，拓展提升

1．感知等式的对称性和传递性

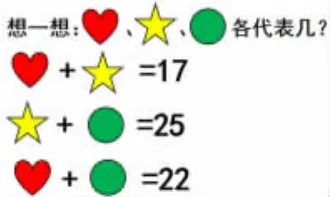
2．交流反馈