盾构机换刀机器人抓取机构夹持力建模分析
赵海鸣,黎焕强,彭正阳,柯威
(1. 中南大学 机电工程学院,湖南 长沙,410083;2. 中国铁建重工集团股份有限公司,湖南 长沙,410100)
盾构机通过安装在最前方的刀具切削前方土体后再由出碴槽排出实现掘进,由于长期在复杂地层工作,刀具会产生剧烈磨损,需要经常更换[1-3]。传统人工换刀方式效率低、风险高,难以满足安全高效施工要求,因此,采用机器人自动换刀很有必要。换刀机器人抓取机构的作用是将质量达200 kg 的滚刀牢固、稳定地夹持,完成刀盘和储存舱之间的替换运输工作。滚刀抓取机构夹持滚刀所需的夹持力是抓取机构的设计依据,要求抓取机构能输出足够大的夹紧力,以防掉落。国外对换刀机器人的设计研究起步较早。2012年,德国人工智能研究中心设计了HECTOR 换刀机器人,但仅用于实验室试验[4];2015年,法国布衣格公司设计了库卡机械臂加末端执行器的换刀机器人,并应用于香港屯门隧道工程[5]。在我国,杨冬建等[6]研究了两侧液压缸式滚刀夹持机构,张海东等[7]研究了一种六自由度换刀机器人,PENG 等[8]对刀架位姿确定的视觉系统进行了研究,XIA等[9]提出并验证了一种四元件的刀具拆卸机构,但大多处于设计阶段。目前,关于滚刀夹持机构的夹持力分析报道很少。关于夹持力的研究主要是传统的锻造操作机构夹持力建模,如:杨晋等[10-11]分析了工件在垂直偏转状态下钳口受力特点,建立了钳口在任意选择角度的夹持力模型;刘艳妍等[12]对钳口和锻件的接触面进行了简化,建立了对应的夹持力模型;王健健等[13]通过建立夹紧效率的数学模型对浮动式动力卡盘静态夹持特性进行了分析;陆小龙等[14]对双V 字夹持机构夹持角钢时的夹持力及其影响因素进行了探讨;吴永宏等[15]基于力封闭原理和弹性线接触理论对机械手夹持接触力进行了准确求解。在间隙圆柱接触力分析方面,LIU等[16]提出了一种使用较广的带间隙圆柱接触应力分布模型,袁英才等[17]分析了运动副间隙对轮转机刀式折页机构性能的影响。
上述研究可为换刀机器人抓取机构的夹持力建模提供参考,但无法直接应用于间隙半圆弧面接触夹持机构结构。为此,本文对已有间隙接触模型进行改进,建立耦合工况下滚刀夹持力模型,以便为后续机械换刀中同类抓取机构的夹持力输出与机构优化提供参考。
1 换刀机器人滚刀抓取机构
换刀机器人抓取机构需要稳定夹持质量为200 kg的一体式滚刀及刀座,实现滚刀在刀盘和储存舱间稳定运输。为了实现滚刀自动拆装,设计一种一体式滚刀及拆装机构,如图1(a)所示。机构上有4个销轴供滚刀夹持机构夹持。滚刀抓取机构由油缸底座、左侧油缸、右侧油缸及对应相连的左右锁钩和四爪盘组成,如图1(b)所示。油缸底座下方的左右两侧分别有1个吊耳,错位布置,分别与左右油缸的缸体连接,其对应的活塞杆分别连接右侧和左侧锁钩,中间的四爪盘与油缸底座焊接连接,锁钩的旋转轴分别布置在四爪盘左右两侧。通过调节左右两侧的油缸,实现锁钩绕销轴旋转,完成对一体式滚刀抓取。
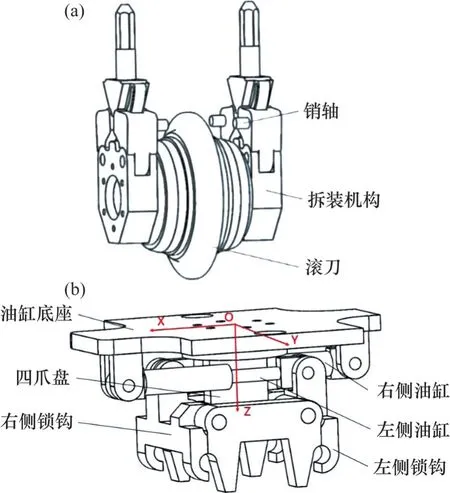
图1 换刀机器人抓取机构结构示意图Fig.1 Schematic diagrams of cutter changing robot grasping mechanism
左右两侧的运动杆件构型相同,因此,分析受力较大一侧即可。左侧抓取机构如图2 所示,3个转动副的转动中心定为A、B和C。现有机构基本参数如表1所示。
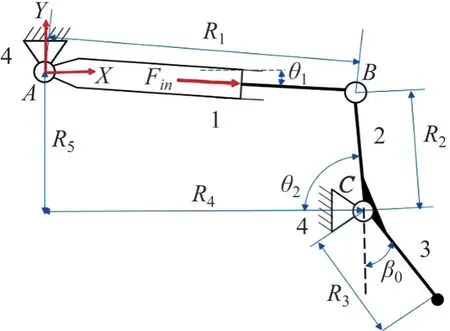
图2 滚刀抓取机构示意图Fig.2 Schematic diagram of hob grasping mechanism
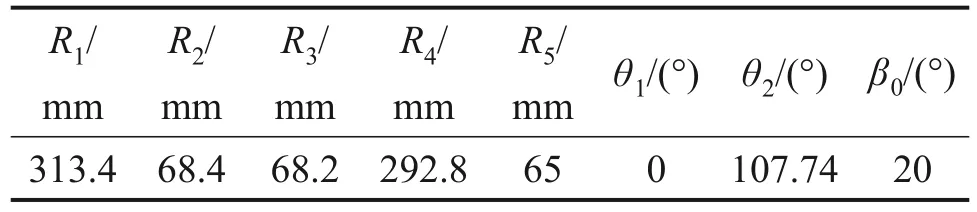
表1 滚刀抓取机构参数Table 1 Parameters of hob grabbing mechanism
2 滚刀抓取机构力学建模
滚刀抓取机构从储存舱运输到前方刀盘过程中存在多种位姿工况,滚刀夹持受载情况差异较大,在此选取主要的水平和竖直工况进行分析,其余工况可基于以上工况或仿照对应工况进行推导。
2.1 销轴接触力模型
基于接触面的应力分布,可得夹持过程中锁钩所受接触力方向。在滚刀夹持机构末端,销轴与半圆锁钩接触,常用的Hertz接触应力分布并不适用于该模型。选取由LIU等[16]推导的误差较小的间隙圆柱接触力模型,表达式为
式中:λ=sin(ε/2);ε为接触半角,(°);Δr为锁钩与销轴半径之差,mm;E*为材料的复合弹性模量,1/E*=1/E1+1/E2,Pa;E1为锁钩材料的弹性模量,Pa;E2为销轴材料的弹性模量,Pa;P为轴线方向单位长度上的外压力,N。
最大接触应力为py0,则接触应力在y向分布为
式中:x为距离y轴的水平距离;l为接触半角对应的弦长,l=2r2sin(ε/2)。模型应力分布如图3所示。
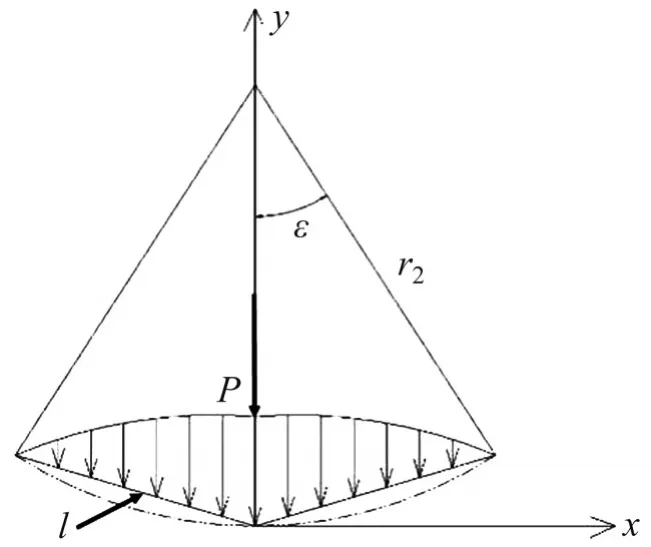
图3 模型中的圆柱接触应力分布Fig.3 Contact stress distribution of cylinder in model
其假设前提条件为:1) 该圆柱体等效为刚性楔,接触压力沿刚性楔廓线的y向分布为Hertz 理论给出的椭球形;2) 等效刚性楔体与弹性地基的接触边界满足几何关系cos(ε)=Δr/(Δr+δ)(其中,δ为最大侵彻位移),该公式来自于Persson[18]的理论模型;3) 圆柱所在平面模型为温克勒弹性地基模型,并受刚性楔块压缩。
该模型只给出了y向的接触应力分布,没有给出销轴的x方向受力。因此,基于条件2),将条件3)的楔形块与温克勒的水平地基模型分别替换为圆柱与垂直于接触面的弹性模型,即可得到含x向分力的接触力。
2.2 夹持力模型
2.2.1 竖直向下工况
已知油缸、锁钩上部和锁钩下部对应的重力G1、G2、G3和滚刀重力G,滚刀抓取机构受力如图4(a)所示,销轴接触力如图4(b)所示。图4 中,Fc为接触力合力,Ff为摩擦力,θ为接触力Fc方向与竖直方向所成的夹角。
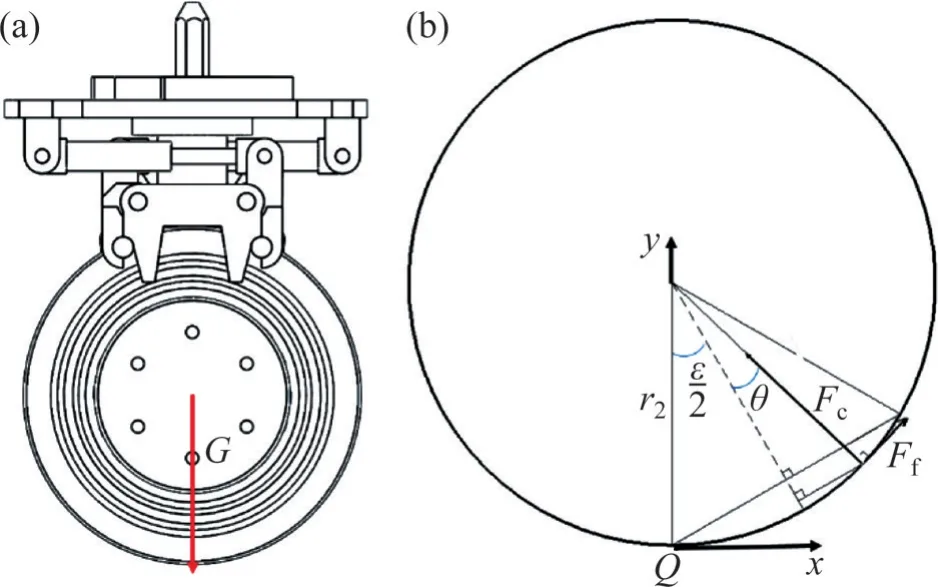
图4 滚刀竖直向下工况示意图Fig. 4 Schematic diagrams of hob vertical downward working condition
在竖直工况下,轴向单位长度载荷p可表达为
式中:h为销轴受力接触线长度。
销轴受力分析如图4(b)所示,Fc相对于Q点的距离lQ为
锁钩和销轴间存在较小位移,但摩擦因数不影响接触力分布[19],因此,Fc和Ff的合力的反力在x向和y向的作用力Fvx、Fvy及其相对转动中心C的力臂lb1和lb2分别为:
力臂与力示意图如图5所示。
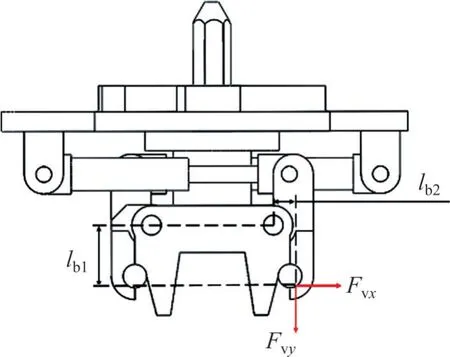
图5 力臂与力示意图Fig.5 Schematic diagram of moment arm and force
由销轴受力平衡可知,Fvy=G/4,但Fvy中摩擦力的影响无法确定,仍无法求解夹持装置的夹持力Fout。Fout的水平分力(Foutx和Fouty)与竖直分力(Fvx和Fvy)为相互作用力。垂直工况下抓取机构受力示意图如图6所示。
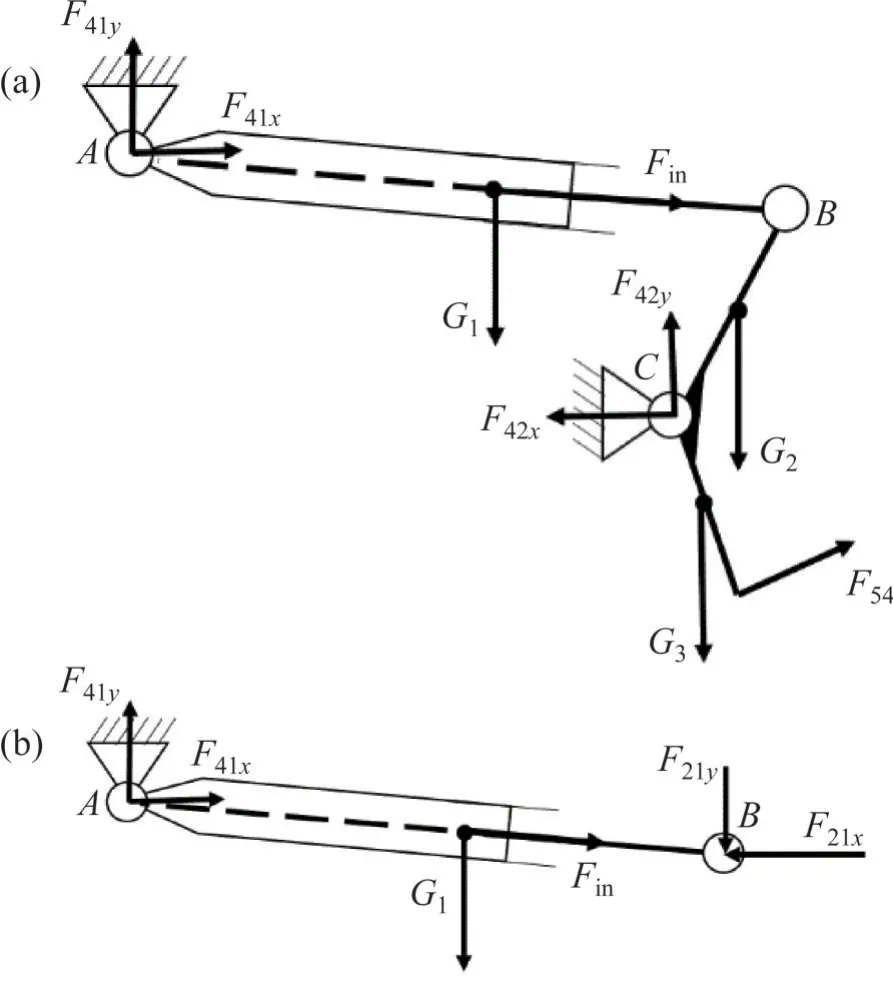
图6 竖直工况下抓取机构受力示意图Fig.6 Stress diagram of grasping mechanism under vertical working condition
对图6中的锁钩和油缸进行分析得:
式中:Fijx为构件i对构件j在x方向的作用力,其余依此类推。
F12x、F12y和Foutx未知,无法求解。根据式(10)可知,Foutx和F12x之和不变,又由式(6)可知Foutx与摩擦力Ff和接触力Fc有关。
建立如图7所示的力学矢量图,并对受力模型进行分类讨论。
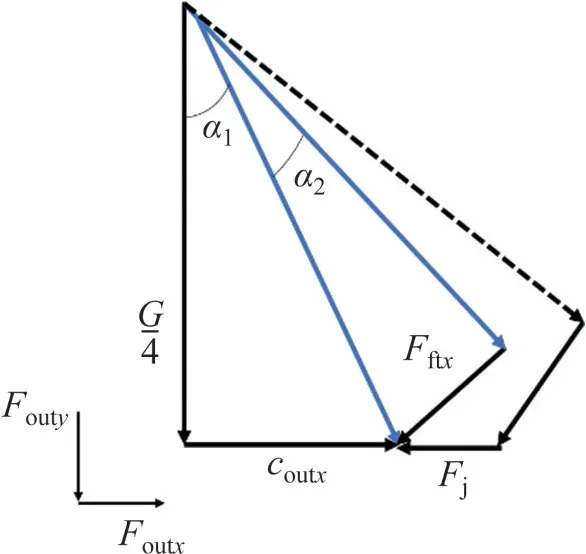
图7 竖直工况下夹持力学矢量图Fig.7 Vector diagram of clamping mechanics in vertical working condition
1) 当F12x恰好为0时,销轴和锁钩接触间无摩擦力。定义coutx为恰好平衡重力矩时的Foutx,联立式(10)和式(11)可得
由图7可知Fc与重力夹角α1为arctan(4coutx/G),联立式(1)、(2)、(5)和(13)求解coutx。
2) 当F12x为0时,所需摩擦力最大,定义此时摩擦力为Fftx=μFccosθ,其中,μ为摩擦因数,得
3) 当F12x不为0 时,Foutx中含有油缸主动夹持力Fj为
综上所述,对竖直向下工况进行分析时,需先对Fc和重力夹角进行分析。当Fc与重力方向夹角小于α1时,对应的Foutx较小,摩擦力为0 N,机构产生顺时针力矩,由限位面平衡Fin为0 N;当夹角介于α1和α2时,摩擦力和接触力共同平衡力矩,油缸输出压力Fin为0 N;当夹角大于α2时,油缸需输出压力Find为
基于表1 中参数,结合式(12)、(13)求解得coutx=231 N,α1=18.1°,α2=8.56°。
Fc与重力夹角为ε/2+θ=15.5°,小于α1;此外,Find=0。
2.2.2 竖直向上工况
工况受力如图8 所示。销轴受力弧面为1/2 圆弧,当锁钩与销轴相对运动时,不存在摩擦滑移,此时,载荷p为
结合式(1)、(2)、(5)和(16),求得该工况的Fc在x向和y向的作用力Fvx和Fvy分别为
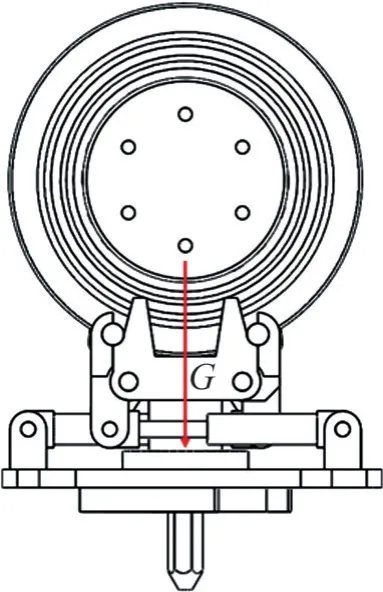
图8 滚刀竖直工况二示意图Fig.8 Schematic diagram of vertical hob working condition II
该工况油缸输出压力Finu为
2.2.3 水平工况
重力在z向时,受力如图9 所示。重力由摩擦力平衡。销轴z向受力作用点简化为接触线中点,所以,图9(a)中的力臂d1=d2=d3=107 mm,d3=167 mm。
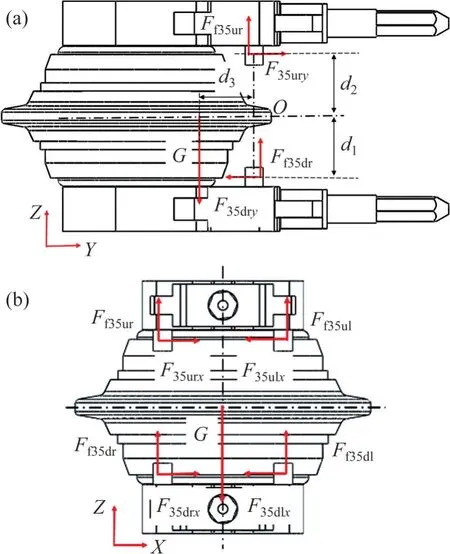
图9 四销轴受力示意图Fig.9 Schematic diagrams of force on four pin shafts
定义FN为x和y方向的合力,
为简化分析,认为Ff35ur和Ff35dr关于销轴中心线对称。由滚刀y向平衡可知F35dry=F35ury,同一锁钩在销轴x方向的压力相等,F35drx=F35urx。同理,销轴的竖直向上的摩擦力均相等。
锁钩与销轴接触形状为1/4 圆,下销轴y向受力F35dry来自于锁钩与四爪盘的2个1/4圆,如图10所示,经简化分析得。锁钩受力如图11所示。
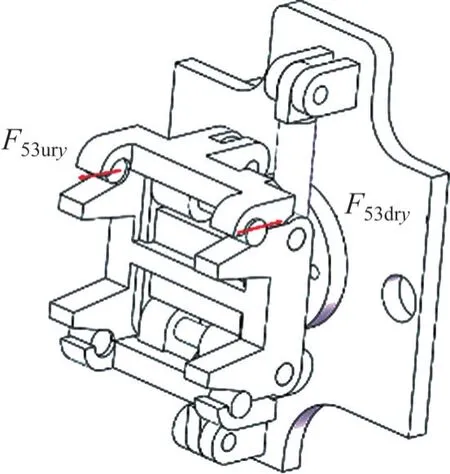
图10 销轴受力包络示意图Fig.10 Schematic diagram of stress envelope of pin shaft
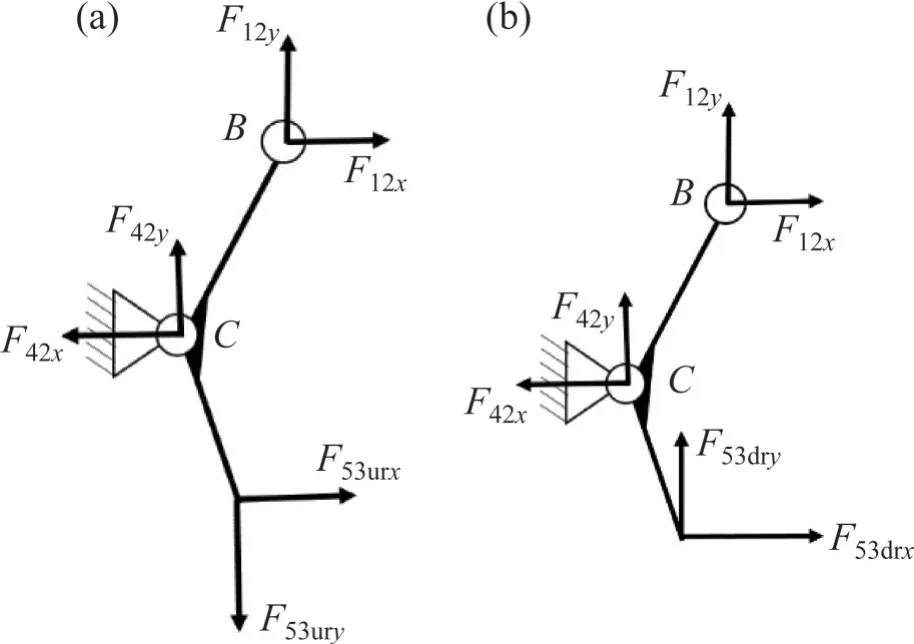
图11 右侧锁钩在不同销轴受力示意图Fig.11 Stress diagrams of right lock hook on different pin shafts
销轴受力合力图如图12 所示。由图12 可知F35urx和F35ury夹角γ为
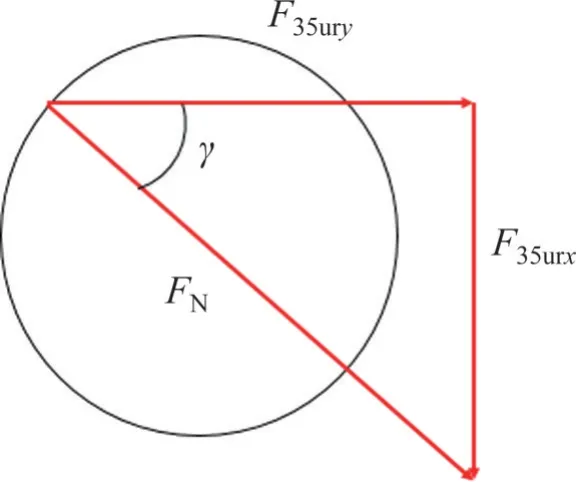
图12 销轴受力合力图Fig. 12 Diagram of force on pin shaft
在水平工况下,将油缸输出力Fin定义为Finh,结合图11和图12对力矩进行分析,可得
将表1中参数值代入式(21)、(24)。由式(21)知FN=4 713 N;由式(24)知Finh=9 373 N。F53urx=F53drx=4 582 N,F53ury=1103 N,F53dry=552 N。
2.2.4 合成工况
在运输中,当滚刀重力G与Finh夹角为k时,位姿如图13所示,此时,夹持力Fin为水平工况夹持力和竖直工况夹持力的合成。
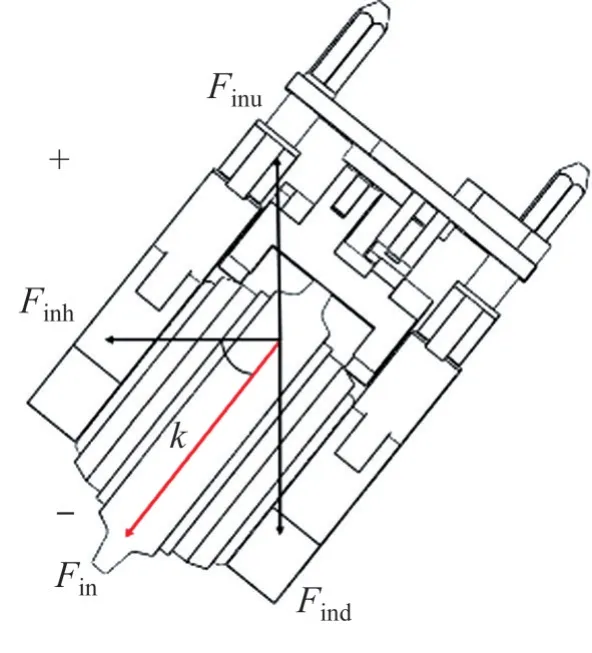
图13 工况示意图Fig. 13 Schematic diagram of working conditions
则夹持力Fin为
理论夹持力曲线如图14所示。
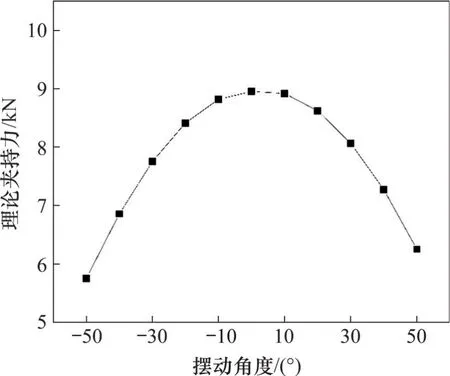
图14 理论夹持力图Fig.14 Theoretical clamping diagram
由图14可知:随着摆动角度k从-50°逐渐增加至50°,夹持力呈现先增大后减小趋势;在0°时夹持力达到最大,为8.95 kN,随后减小。这是由于Finh相对Find和Finu较大,且Finh在Fin的系数为cosk,因此,夹持力理论值曲线随着摆动角度k增大先上升后下降。
此外,当摆动角度为-50°时,夹持力理论值为5.76 kN;当摆动角度为50°时,夹持力理论值为6.01 kN;即摆动角度为-50°到0°时的夹持力比0°到50°对应的夹持力小。由式(25)和(26)可知,Finh与Fin的系数均为cosk,但式(26)中的Finu比式(25)中Find的大,因此,曲线不对称。
3 滚刀抓取机构仿真分析
3.1 滚刀抓取机构仿真模型
将滚刀抓取机构模型导入ADAMS中,设置机构的约束关系,根据夹持机构抓取滚刀的过程在ADAMS 设置对应运动约束。2 种工况下的滚刀抓取机构最终约束模型如图15所示。
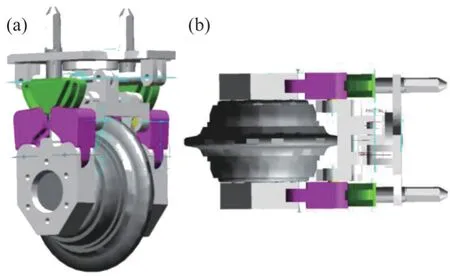
图15 最终约束模型Fig 15 Final constraint models
仿真接触参数设置如表2所示。

表2 接触参数Table 2 Contact parameters
3.2 夹持力结果分析
3.2.1 竖直工况
由竖直工况理论推导可知,竖直工况下油缸所需输出力为0 N,因此,不对该工况仿真设置驱动,在重力下对比验证临界角α1或α2即可,仿真结果如图16所示。
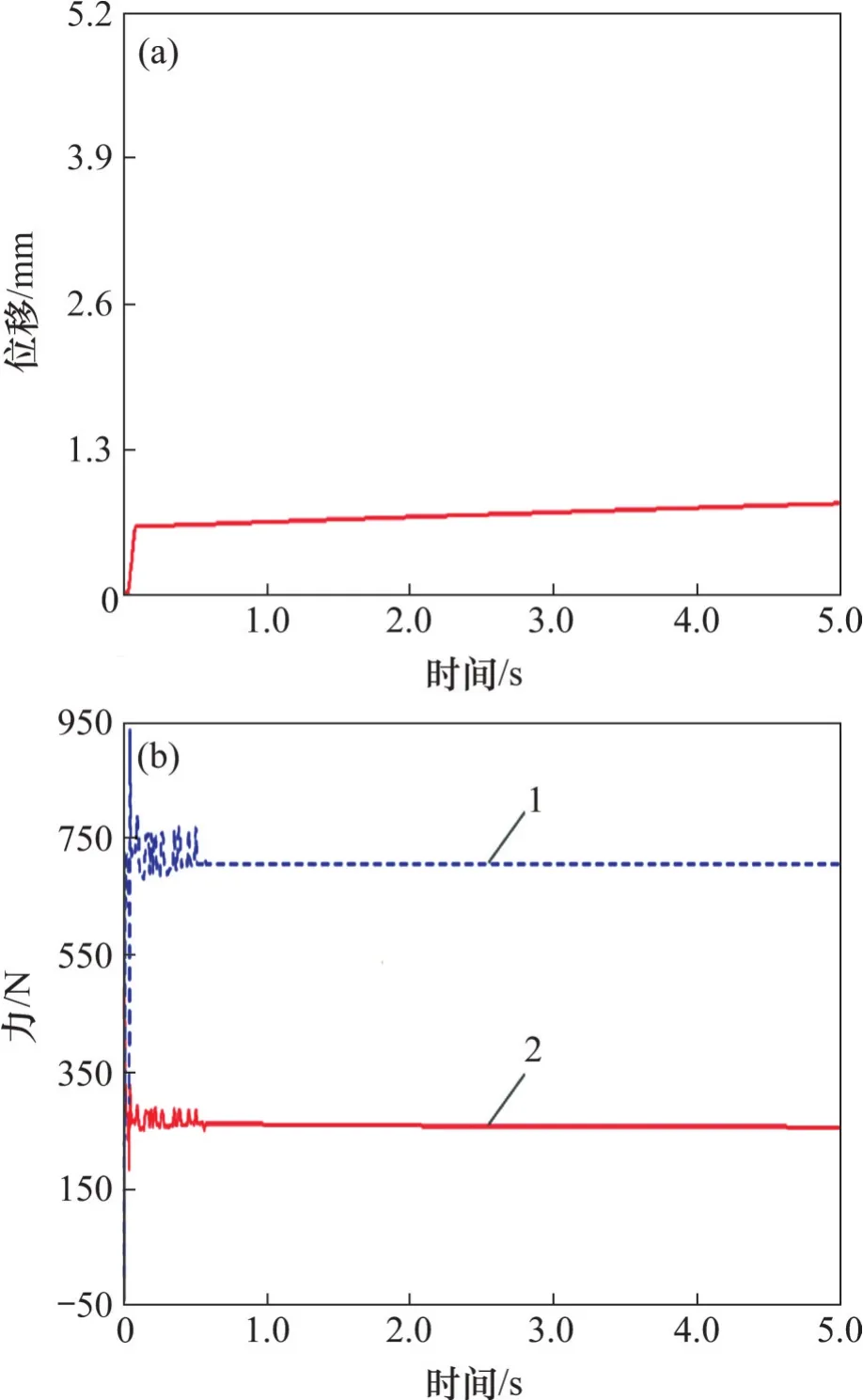
图16 ADAMS竖直向下工况仿真图Fig.16 Simulation diagram of ADAMS vertical downward working condition
除去冲击位移外,滚刀在重力中的作用下位移基本为0 N,F53x=257 N,F53y=709 N。理论夹角α1对应的仿真夹角α1p为
竖直工况下仿真值与理论值对比如表3所示。

表3 竖直工况下理论值和仿真值Table 3 Theoretical and simulation results of vertical working condition
理论值和仿真值存在一定误差,该误差来源于:1) 将销轴考虑为楔形刚体,理论接触面与实际接触面不同;2) 仿真刚开始时,在重力作用下对锁钩存在刚性冲击,冲击力远大于理论值。
竖直工况理论模型解释了摩擦力与接触力之间的关系。
3.2.2 水平工况
据水平工况的理论推导可知,水平工况由摩擦力平衡,仿真过程只能设置油缸推杆的推力。在此仿真驱动设置为:在油缸处沿推杆方向设置单向力,通过不断调试推杆推力,直至达到临界平衡。
考虑到夹持机构从力的加载到稳定夹持需要一定时间,在此时间内销轴会发生位移,影响夹持,因此,设定滚刀前2 s 固定,待锁钩与销轴接触后,取消滚刀固定约束,再据仿真结果判断是否稳定。取夹持力Fin分别为9 650、9 850 和100 50 N,得到一体式滚刀的质心加速度变化,如图17所示。
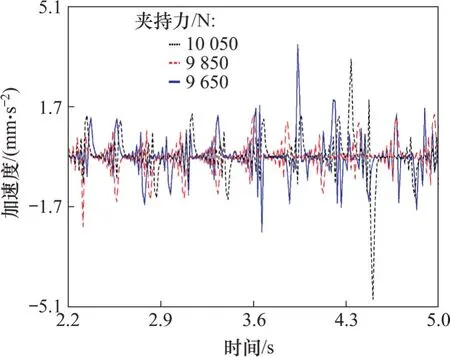
图17 滚刀质心加速度Fig.17 Acceleration of hob centroid
前2 s滚刀机构固定,因此,只分析2 s后的加速度。从图17 可知:相比于100 50 N 和9 650 N,当夹持力为9 850 N时,滚刀加速度峰值减小,且与100 50 N 时的滚刀加速度变化幅度相同,由此可知水平工况夹持力为9 850 N。销轴受力结果如表4所示。

表4 水平工况下销轴受力理论值和仿真值Table 4 Theory and simulation results of force on pin shaft in horizontal working condition
由表4可知在水平工况下,理论与仿真结果存在一定误差,其主要原因是简化了模型接触点位置,认为接触点在y向关于销轴对称,没有得到F53ur和F53dr相对O点较准确的力矩;F53dry接触面压力存在简化,没有考虑变形和锁钩压力的影响,造成理论值偏低。
4 滚刀抓取机构实验
4.1 滚刀抓取机构实验装置与实验过程
依托铁建重工的换刀机器人工况模拟试验台开展试验研究,结构如图18所示。

图18 换刀机器人工况模拟试验台Fig.18 Working condition simulation test benchs of tool changing robot
拆装机构将滚刀与刀箱分离后,夹持机构伸入刀箱内抓取滚刀后平移抽出,将机械臂关节均调节至水平初始位姿,对滚刀抓取机构11 种位姿进行模拟,回转关节角为0°,摆动关节摆至-50°,其位姿如图19(a)所示;以10°为间隔逐渐增大至50°,其位姿如图19(b)所示。

图19 滚刀抓取机构多工况实验图Fig.19 Multi-working experimental diagrams of hob clamping mechanism
4.2 滚刀抓取实验结果分析
通过油压传感器可读取抓取油缸在不同工况下的压力,结合油缸尺寸,将油缸压力T换算成油缸推杆推力F。
式中:F为推力,N;ΔT为油缸压力差,MPa;D为油缸内径,油缸内径为40 mm。
对由2种位姿耦合而成的11种工况进行测试,得到对应油缸输出力,如表5所示。

表5 不同位姿下抓取油缸推力Table 5 Grasping cylinder thrust forces under different poses kN
根据表5中的不同工况条件进行仿真,将仿真值、实验组分理论夹持力进行对比,结果如图20所示。
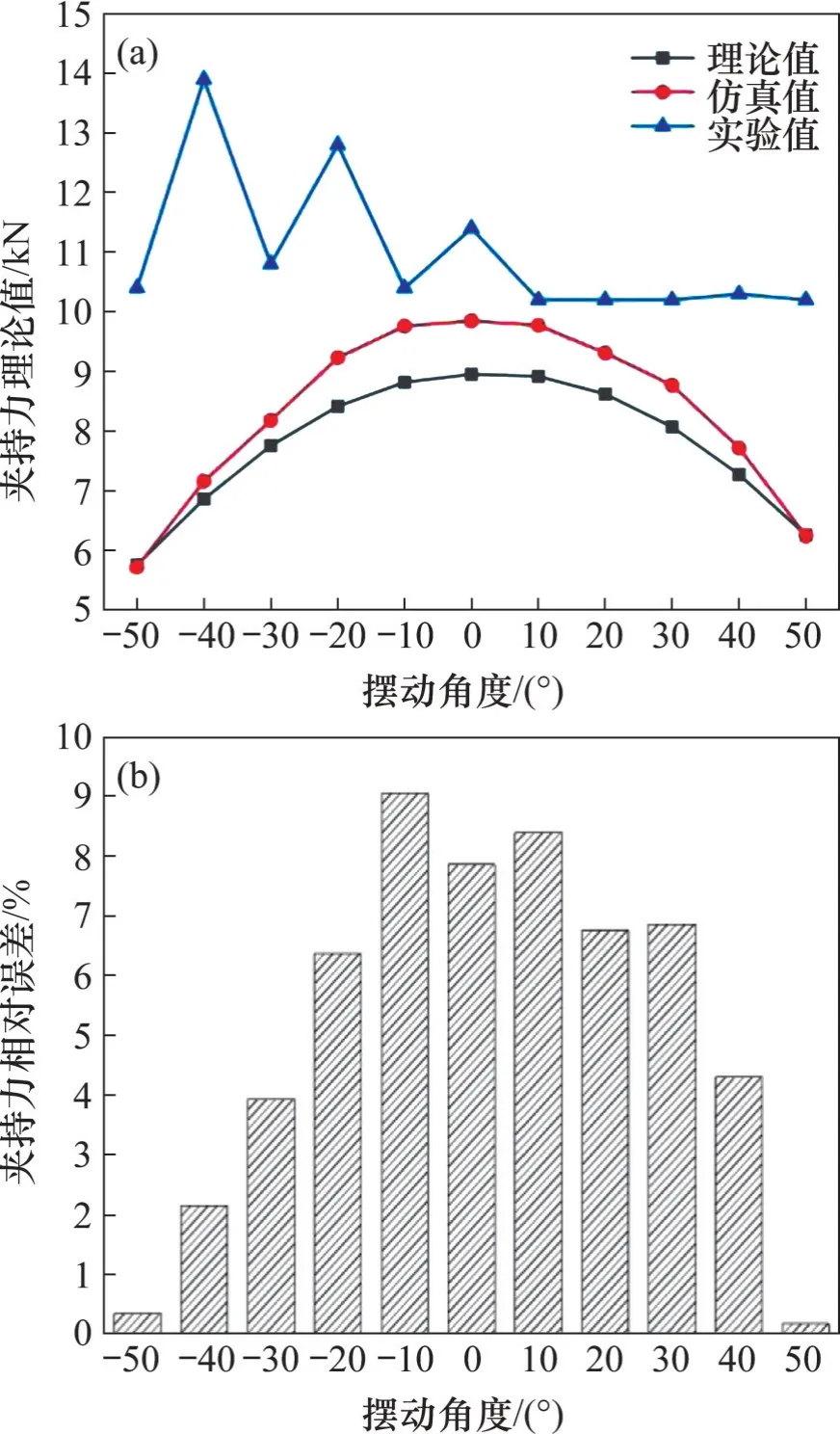
图20 滚刀抓取机构不同摆动角度的夹持力对比Fig.20 Comparison of holding force of hob clamping mechanism at different swing angles
由图20(a)可知:夹持力实验值曲线在仿真值曲线和理论值曲线上方,数据在10~14 kN 之间波动,但基本稳定在10.2 kN。在实验过程中,由于机构末端负载无法反馈给油缸,为保证安全,油缸压力设置为略大于仿真最大值。因此,实验值与仿真值和理论值并不相同,而是基本稳定在10.2 kN附近。
而夹持力理论曲线与仿真曲线贴合程度高,且变化趋势相同,说明了理论模型的可靠性,如图20(a)所示。
夹持力理论值与仿真值的相对误差如图20(b)所示。从图20(b)可见:随着摆动角度不断增大,夹持力仿真值与理论值的相对误差η先增大后减小。结合式(25)、(26)及前述理论分析可知,在0°附近时,相对误差最大,此时,理论模型的误差主要来源于Finh;而在50°和-50°时,误差主要来源于采用小间隙销轴接触理论部分推导的Find和Finu,相对误差最小;模型整体相对误差均在10%以内,证明了夹持力模型的准确性。
5 结论
1) 基于小间隙圆柱接触模型,建立了换刀机器人抓取机构在竖直和水平这2种典型工况下的夹持力数学模型,并得到不同摆动角度下所需的最小夹持力,为夹持机构夹持力输出和优化提供了依据。
2) 通过ADAMS 软件对11 种由竖直工况和水平位姿耦合的工况进行仿真分析,夹持力仿真结果与理论结果的相对误差在10%以内,验证了夹持力模型的准确性。

