旋转辊差异化非直流道设计与多目标优化方法
李铖,姜海蛟,李永康,2
(1. 太原理工大学 机械与运载工程学院,山西 太原,030024;2. 太原经济技术开发区 博士后科研工作站,山西 太原,030032)
非晶薄带具有优良的物理和电磁性能,被广泛应用于航空航天、变压器与传感器等领域[1],目前主要采用平面流铸法制备非晶薄带。冷却辊作为平面流铸的关键设备,其换热特性与效率直接影响非晶薄带的质量,特别是随着非晶薄带制备宽度的增大,对其换热效率提出更高要求。冷却辊高速旋转,流道内水流受力与流动特性较复杂,而流道结构决定了辊内冷却水流动特性与更新速率,设计具有高换热效率的冷却辊流道结构,对提高非晶薄带的横向厚度均匀度、改善带体脆化与系统节能具有重要意义[2]。
众多学者对旋转辊内流道的流动特性进行了研究。SONG 等[3]设计了3 种采用直肋道的旋转冷却辊流道,使用CFX 数值模拟获得了流道内压力与流线分布情况;郭茜等[4]为降低冷却辊表面温度,采用有限元法对冷却辊进行数值模拟,得到了辊外径、辊速、辊厚与温度之间的关系。为进行结构优化,BEIGZADEH 等[5]结合数值模拟与神经网络技术得到了间断板翅的最优参数。针对多变量、多参数优化问题,GUERRINI 等[6]采用Plackett-Burman试验对木材削片过程中的影响变量进行了筛选,简化了设计过程。现有研究主要针对散射状直肋道,且仅限于采用数值模拟方法对其流动特性开展研究,尚未从流道内流体微团力学分析角度出发,探究流道型线与旋向的关系对流动特性的影响,无法为肋道型线设计与优化提供理论支撑。另外,由于进、出水面的水流方向不同,若采用统一的径向直流道,则水流方向会直接影响其流动特性,因此,有必要开展结构差异化设计,从结构角度出发对流道进行研究。
为提高冷却辊流道内水流的更新速率,在流道内流体微团力学分析基础上,提出一种进、出水面差异化的非直流道结构;针对使用流体动力学方法进行多变量、多参数优化时效率低的问题,在提出流道综合性能指标的前提下,采用BP神经网络预测与遗传算法优化相结合的多目标优化方法对冷却辊进、出水面的肋道进行优化,以期获得最优的流道构型。
1 冷却辊流道结构与改进方法
1.1 传统散射状直流道结构
目前,广泛应用于平面流铸的冷却辊散射状直流道结构如图1所示。冷却辊内芯两侧分别有若干由肋道与侧板形成的封闭进、出水面流道。冷却水由进水口进入空心主轴,经进水面流道进入环形换热通道与辊套换热,再经出水面流道从主轴出水口排出。冷却辊换热效率取决于换热通道内水流更新速率,而在外界条件一定的前提下,流道结构决定了水流更新速率。然而,随着冷却辊高速旋转,现有直流道存在冲击、涡旋等现象,不仅造成能量损失,也极大影响了冷却辊换热效率[7]。
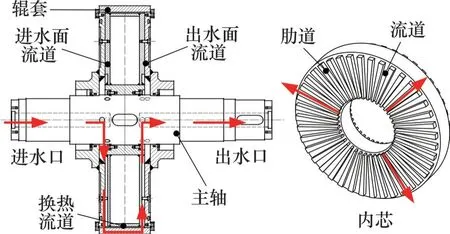
图1 冷却辊散射状直流道结构Fig. 1 Structure of scattering straight channel of cooling roller
1.2 流道内流体微团力学分析与改进方法
从流道内流体微团的力学分析角度出发,可在理论层面为流道结构优化提供依据。以如图2所示的进水面流道为例,设冷却辊以角速度ω逆时针旋转,当肋道的旋向与冷却辊转向相反时,质量为dm的流体微团在流道内以相对速度w沿着流线方向作相对运动。对流道微团进行力学分析可得沿法线t方向的平衡方程为
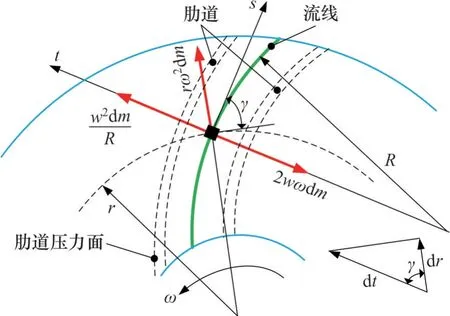
图2 进水面流道流体微团力学分析Fig. 2 Force analysis of fluid micelles in the inlet surface flow channel
式中:∂p/∂t为法线t方向的压力梯度,Pa;ρ为流体密度,kg/m3;γ为相对速度w与圆周速度u反方向的夹角;r与R分别为微团所在流道半径与流线曲率半径,m;w2dm/R与rω2dm分别为微团沿着流线运动时产生的离心力与微团随进水面流道作旋转运动产生的离心力,N;2wωdm为哥式力,方向指向曲率中心,N。
流体微团在法线t方向满足如下偏微分方程:
由于流体微团的圆周速度u=rω,由t方向微元dt与半径r方向微元dr的关系可知dt=dr/cosγ,代入式(2)可得
对比式(1)可得流体微团相对运动在法线方向的速度梯度∂w/∂t=2ω-w/R。同理,当肋道旋向与冷却辊转向相同时,∂w/∂t=-(2ω+w/R);当肋道为径向时,∂w/∂t=2ω。
流道内相对速度梯度绝对值越大,轴向涡旋越严重[8]。为改善现有流道涡旋现象,进水面应选择旋向与冷却辊转向相反的肋道,如图3(a)所示;出水面则选择旋向与冷却辊转向相同的肋道,如图3(b)所示。
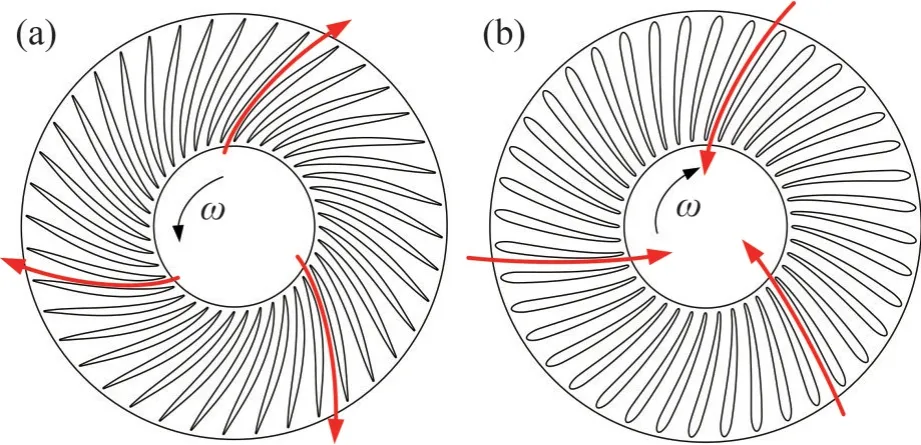
图3 新型差异化非直流道Fig. 3 New differential non-straight channel
2 非直流道参数化建模与分析
2.1 基于Bezier曲线的参数化建模
图4所示为非直肋道的部分设计参数,具体含义如下:α为肋道进口安放角;β为肋道出口安放角;δ为肋道包角;l为肋道外侧宽度。
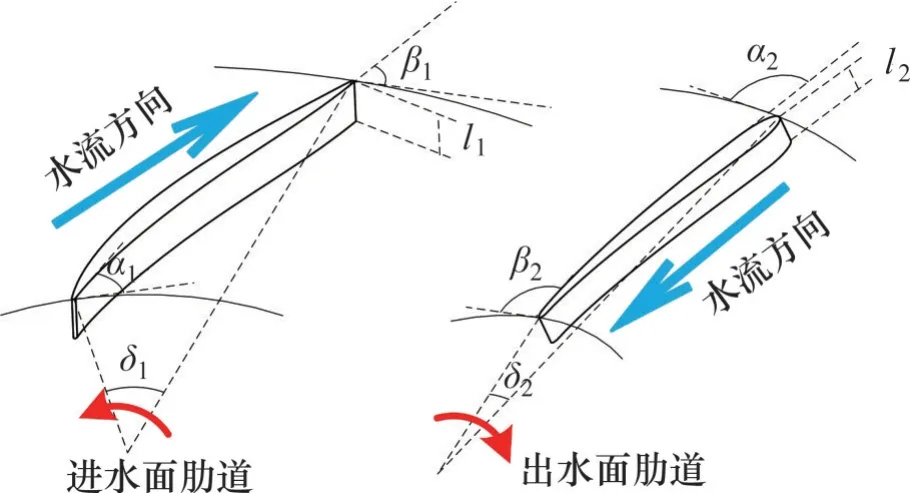
图4 肋道具体参数Fig. 4 Specific parameters of the rib
参数化模型的建立可极大提高后期优化效率,为此对肋道厚度进行参数化表达。Bezier曲线具有优异的凸包性和全局性,被广泛应用于现代曲线设计[9]。采用Bezier曲线实现肋道的加厚,其方法是通过k+1个控制点来决定k阶Bezier曲线的形状。本文采用4 阶Bezier 曲线来对肋道的厚度进行控制。图5(a)中,x1、x2、x3分别为进水面肋道加厚的可变控制点1、2、3 对应的肋道厚度;图5(b)中,y1、y2、y3为出水面肋道加厚的可变控制点1、2、3对应的肋道厚度。
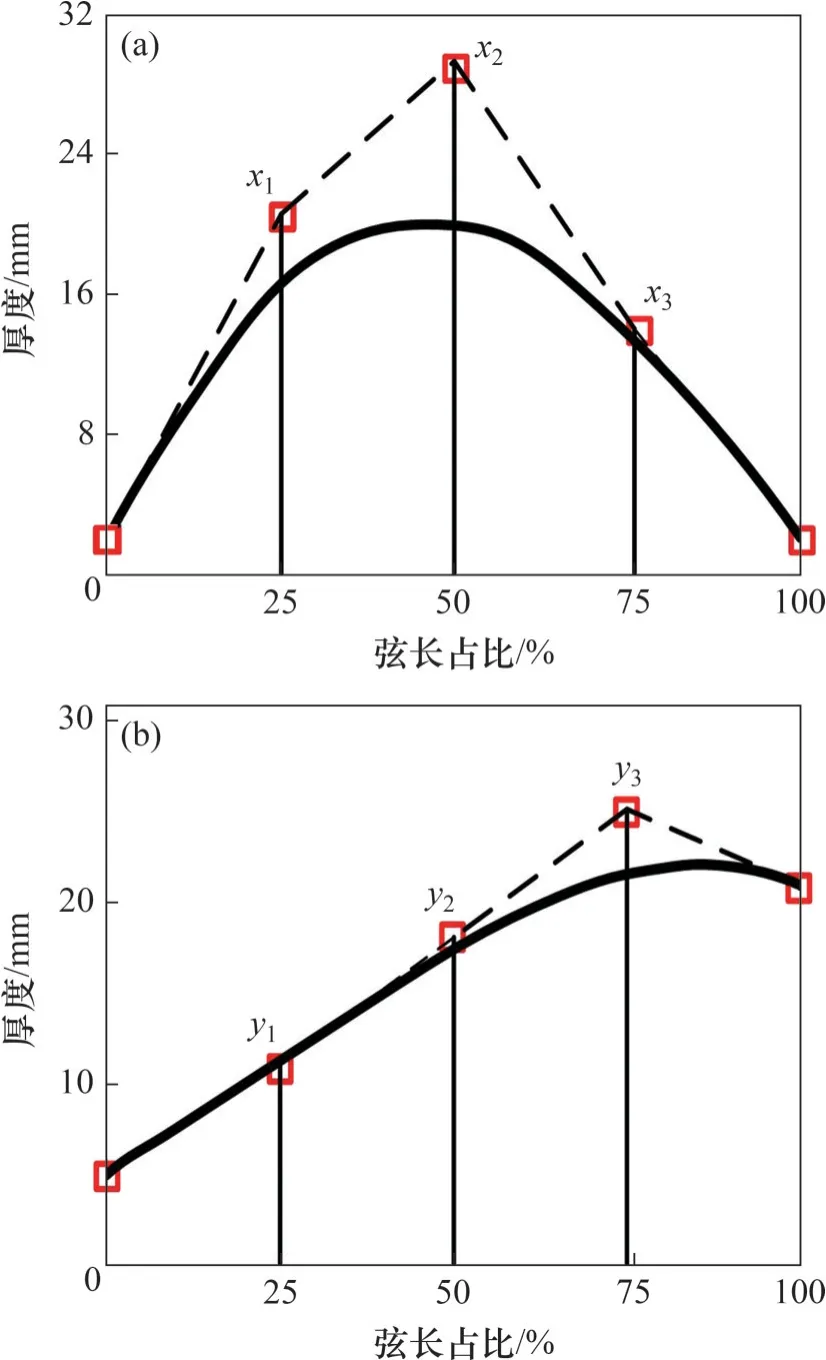
图5 肋道参数化加厚Fig. 5 Parametric thickening of rib
2.2 初始参数的确定
通过理论分析获得冷却辊肋道进口安放角、出口安放角、包角与宽度等初始设计参数,如表1所示。采用交互式叶轮设计软件Blade Gen对冷却辊肋道进行建模[10]。
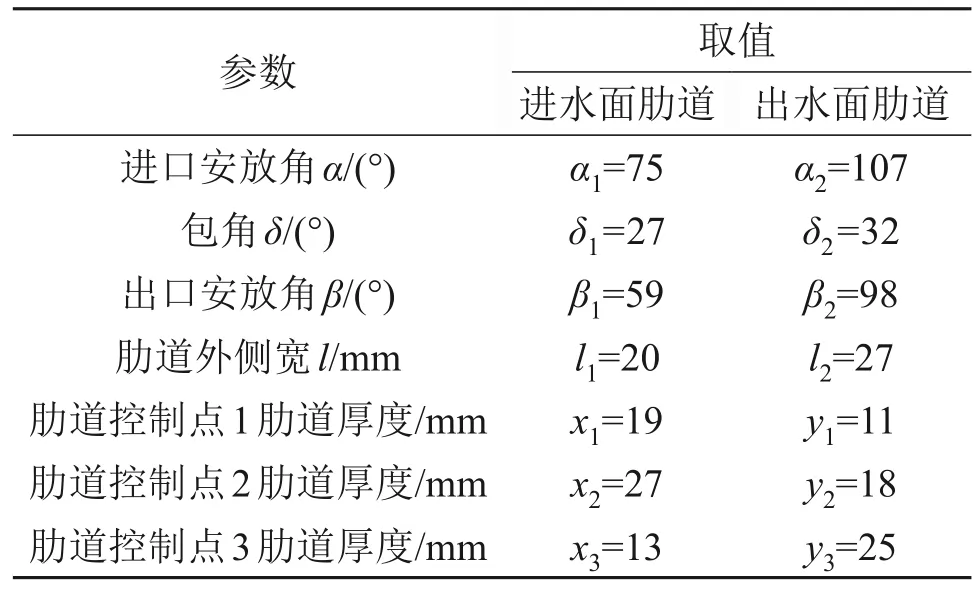
表1 冷却辊结构几何参数Table 1 The geometrical parameters of the cooling roller structure
2.3 流动特性求解过程
针对结构较为简单的圆环状换热通道,采用传统Mesh软件划分六面体网格。进出水面流道较复杂,为提高求解精度,采用Turbo Grid专业化软件进行高质量结构化网格划分,该软件可自动加密流道边界区域[11],划分结果如图6所示。

图6 冷却辊流道网格分布Fig. 6 Grid distribution of cooling roller channel
由于冷却辊流道较复杂,需进行网格无关性检验来保证试验的准确性[12]。不同网格数下冷却辊出口流量Q与换热通道轴向速度v的对比见表2。由于4种方案所得结果基本一致,为节省时间和节约资源,选择方案1进行网格划分。
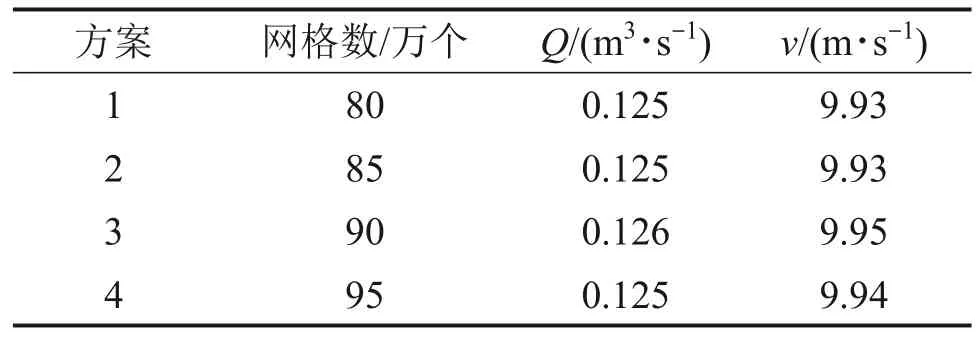
表2 网格无关性验证Table 2 Grid independence verification
采用标准k-ε湍流模型对流道内流体的流动特性展开研究。根据实际工况设置冷却辊的旋转速度为378 r/min,进水面流道入口压力设置为0.1 MPa,出水面流道出口压力设置为0 MPa。
冷却辊肋道、侧板、轮毂等设置为无滑移壁面,进水面流道与换热通道的接触面选择为通用连接。采用高阶精度进行求解,迭代次数设置为100,收敛精度设置为10-4,采用Expressions 功能对相关参数进行监测。
3 流道多目标优化方法
由于影响流道流动特性的结构参数较多,且进、出水面流道目标函数存在差异,单组流体动力学仿真计算量大,优化过程极为复杂。为此,本文综合运用BP 神经网络和GA 遗传算法,以期提高冷却辊流道优化时的效率。优化流程如图7所示。
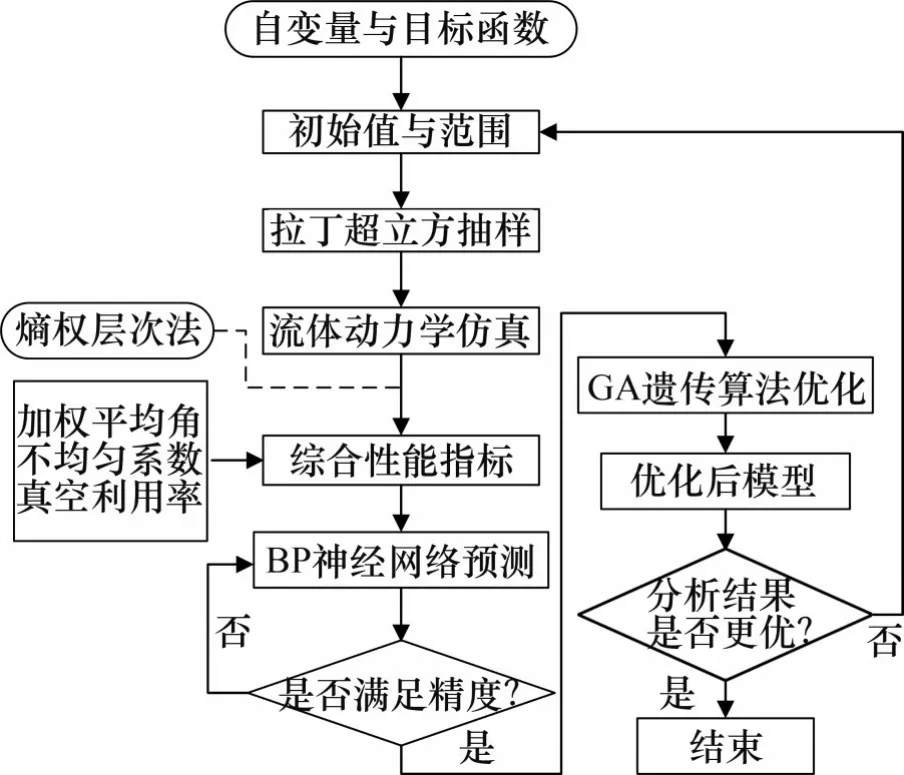
图7 优化流程Fig. 7 Optimization flow chart
分步对进、出水面流道进行优化,首先,确定影响流道换热效率的目标函数,进一步采用Plackett-Burman试验,选出对目标函数影响显著的自变量;然后,采用拉丁超立方抽样方法选择样本,进一步对样本进行流体动力学仿真,基于熵权层次分析法获得综合性能指标;在多组样本计算基础上,通过BP神经网络对特定自变量参数下的目标函数进行预测,在此基础上采用GA遗传算法进行寻优,直至获得最优解。
3.1 目标函数与自变量确定
3.1.1 目标函数确定
1) 加权平均角。换热通道内水流轴向速度分量越大,越利于提高水流的更新速率。为提高换热通道轴向速度分量,引入加权平均角θ来描述换热通道流速的垂直度。当θ越接近90°,水流越垂直于换热通道截面时,越有利于水流快速流过换热通道,从而避免形成环流[13]。
式中:uyi为换热通道截面切向速度,m/s;uxi为换热通道截面法向速度,m/s。
2) 不均匀系数。流场速度不均匀会产生涡旋现象,降低冷却辊水流更新速率。为减小流道水流速度梯度,使流体流动更均匀,引入不均匀系数ξ。
式中:vmax为进水面流道出口最大速度,m/s;vmin为进水面流道出口最小速度,m/s;vave为进水面流道出口平均速度,m/s。为使目标函数统一为求最大值,将不均匀系数ξ变为1/ξ进行计算。
3) 吸入真空度利用率。吸入真空度利用率η即流道的效率,是进行优化的重要指标之一。流道效率越高,流体损失越小。在进水面流道,机械能转化为流体能量,则进水面流道效率的计算公式为
式中:ρ为流体密度,kg/m3;g为重力加速度,m/s2;Q为冷却辊流量,m3/s;扬程H=(Pout-Pin)/(ρg),m;Pin和Pout分别为进水面流道进出口总压,Pa;M为进水面流道叶轮转矩,N·m;n为冷却辊转速,r/min。
3.1.2 自变量及初始范围确定
进水面流道自变量较多,部分参数对目标函数影响显著,而剩余参数对目标函数影响不显著。为简化优化过程,采用设计软件Design Expert 进行Plackett-Burman 试验,选出对进水面流道目标参数影响显著的自变量。根据之前流道的参数化数据可确定需要筛选的参数有进口安放角α1、包角δ1、出口安放角β1、肋道外侧宽度l1、控制点x1对应厚度、控制点x2对应厚度和控制点x3对应厚度。
表3所示为筛选参数对目标函数影响的显著性分析。P反映了影响的显著性水平,当P>0.1 时,可认为筛选参数对目标函数影响不显著;当0.05<P≤0.1 时,可认为筛选参数对目标函数影响较显著;当P≤0.05 时,可认为筛选参数对目标函数影响极显著[14]。
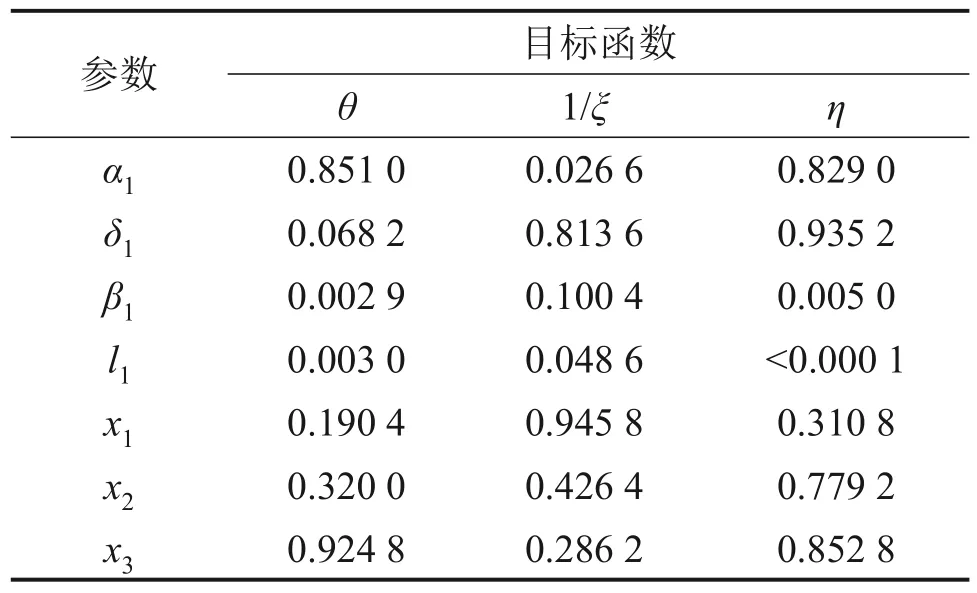
表3 显著性水平分析(以P表征)Table 3 Analysis of significance level(represented by P)
根据显著性水平分析表,取进口安放角α1、包角δ1、出口安放角β1、肋道外侧宽度l1这4 个自变量进行优化设计,并根据加工与强度等要求初步确定自变量取值范围:α1∈[55°, 80°],δ1∈[10°, 40°],β1∈[50°, 80°],l1∈[10, 30] mm。
3.2 样本数据库建立与多目标决策权重确定
3.2.1 样本数据库建立
基于具有均匀分层特性的拉丁超立方抽样技术,采用Matlab 得到如图8 所示的60 组样本数据[15]。
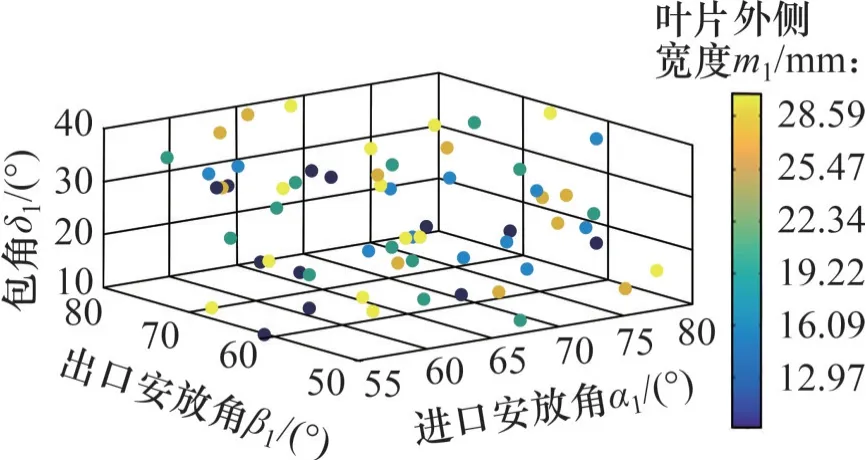
图8 样本空间分布Fig. 8 Sample spatial distribution
根据样本数据,保持换热通道和出水面流道模型不变,在Blade Gen软件中建立60组进水面流道模型。利用CFX 软件中Expressions 功能对加权平均角θ、不均匀系数的倒数1/ξ和吸入真空度利用率η这3个目标函数进行计算,可得到自变量与目标函数对应的数据库。
3.2.2 多目标决策权重确定
在进行寻优之前,需要确定各个目标函数所对应的权重。为使权重更加客观且符合实际要求,本文采用一种改进的熵权层次分析法[16]。
熵权法是依据之前建立的数据库进行计算的,若某目标函数对应的信息熵越小,则其提供的信息量越大,该目标函数所对应的权重也越大。采用熵权法得到的计算结果更客观,决策可信度也更高,其具体计算过程如下。
设有z个试验方案,h个目标函数,则z个实验方案关于h个目标函数的评价矩阵为
由于各目标函数单位不同,采用式(3)将数据范围限制在[0,1]内,即
则第j个目标函数的熵ej为
式中:K=(lnz)-1,各目标函数的熵的权重为
层次分析法是依据主观经验来判断各项目标函数重要程度的一种加权方法[17]。在对目标函数的重要程度进行两两比较后,得到如表4 所示的结果。

表4 层次分析法分析结果对比Table 4 Comparison of analysis results of analytic hierarchy process
表4中的各数值代表该数值所在行的目标函数与所在列的目标函数之间重要程度对比情况,即数值越大,表明该数值所在行的目标函数比所在列的目标函数越重要;数值越小,表明该数值所在行的目标函数比所在列的目标函数越不重要。进一步将表中的数值转化为矩阵A33,为判断矩阵的一致性,采用式(11)对一致性比率SCR进行计算。
式中:一致性指数SCI=(λ-h)/(h-1),由此可得随机一致性指标SRI=0.58,经计算可得矩阵A33的最大特征值λ=3.009 2,代入式(11)可得SCR=0.008,低于0.100,通过一致性检验。对最大特征值λ对应的特征向量进行归一化得到权重系数w。
结合熵权法所得权重系数s和层次分析法所得权重系数w可计算出综合权重系数f,即
结合样本数据可求得熵权法权重系数s=(0.32,0.37,0.31),根据主观经验可得层次分析法权重系数w=(0.54,0.30,0.16),将相关数据代入式(12)可得综合权重系数f=(0.52,0.32,0.16)。
3.3 BP神经网络建模与预测
针对多变量与多参数条件下优化效率低下的问题,采用BP 神经网络对其目标函数进行预测。如图9(a)所示,BP 神经网络包括输入层、隐藏层和输出层3部分,可实现输入层与输出层的非线性映射关系[18]。完整的BP 神经网络训练过程如下:样本数据通过输入层进入神经网络后,在隐藏层进行计算,将输出结果与期望值进行比较,得到误差。在神经网络中进行反向传播,最后通过计算误差信号来修改隐藏层的权重,这一过程称为一次迭代,直到误差满足要求,迭代停止。
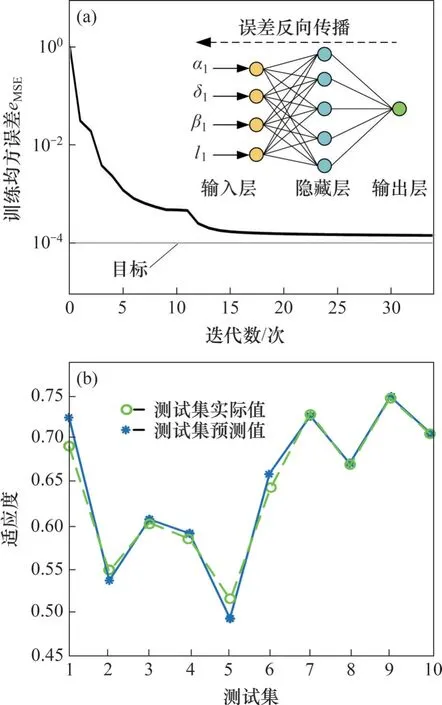
图9 BP神经网络预测Fig. 9 BP neural network prediction
为消除量纲对数据分析的影响,对各目标函数值进行归一化处理。
式中:x和y分别为归一化前、后的函数值;umax和umin分别为同一目标函数对应的最大值和最小值。
将归一化数据与综合权重系数f相结合可得综合目标函数F。将自变量与综合目标函数F导入神经网络中,选取50组作为训练集,剩下10组为测试集。随着迭代次数增加,训练均方根误差不断下降,直至收敛。图9(b)所示为测试集中的预测值与实际值对比,其中预测误差最大值为4.6%,说明该预测模型具有较高的可靠性,预测结果较准确。
3.4 GA遗传算法寻优
遗传算法采用自然界“优胜劣汰”的思想,通过模拟竞争过程中寻找最优目标的方法来形成算法。该算法通过选择、交叉和变异来保留适应度高的优良个体,从而逐渐寻找到最优解[19]。本文设置迭代次数为100、种群规模为20 来进行寻优,从而得到最优值与自变量数值。在进水面流道优化完成后,采用同样的方法对出水面流道进行优化,最终寻优结果如表5所示。
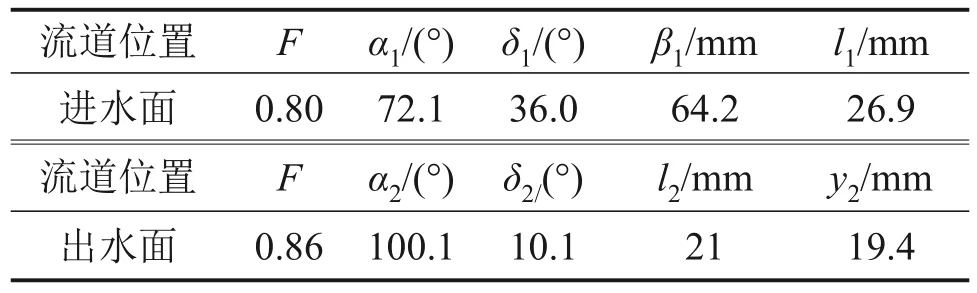
表5 进、出水面流道优化结果Table 5 Optimization results of inlet and outlet flow channels
4 结果与分析
轴向换热通道是冷却水与辊套热交换的区域,而进水面流道的流动特性将影响其水流更新速率,为此主要讨论进水面与轴向换热通道内的流动特性。
4.1 进水面流道内流动特性
图10 所示为改进前后的进水面流道在不同半径处的压力对比。从图10 可见:随着半径增大,流体静压逐渐上升,与离心式叶片泵的静压分布相一致[20],特别是在入口段,新型流道静压较为平坦,流速分布更为均匀,能量损失较小;在进水面流道出口处(半径R=440 mm),优化后非直流道的静压高于散射直流道与优化前非直流道的静压,可使冷却水快速流过换热通道。同时,优化后非直流道的动压明显低于散射直流道动压,有利于减小进水面流道出口与换热通道的冲击。
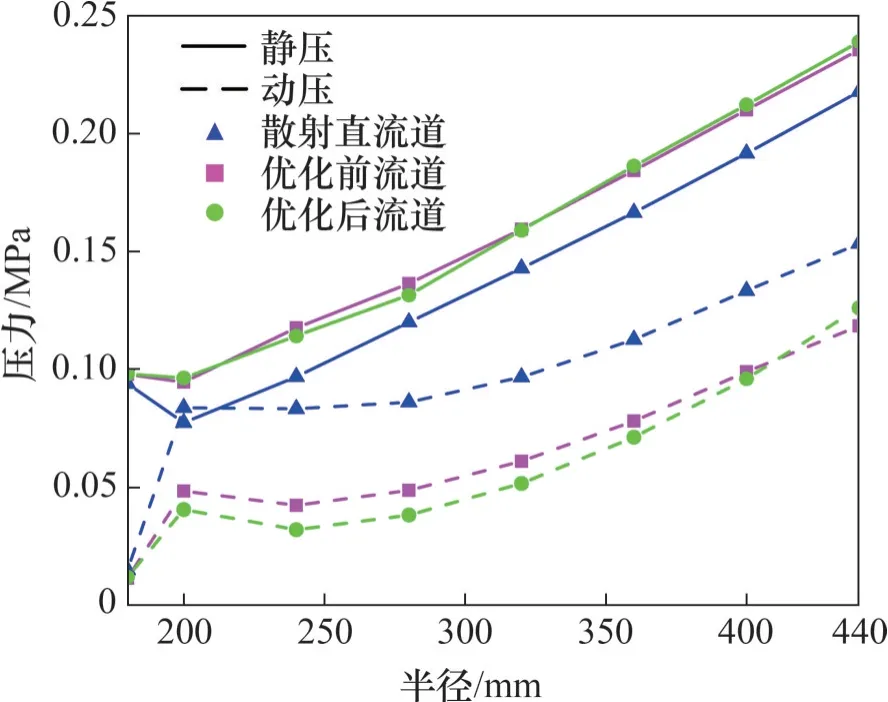
图10 进水面流道静压与动压对比Fig. 10 Comparison of static pressure and dynamic pressure of the flow channel on the inlet surface
图11 所示为进水面流道内水流速度矢量与静压对比。由图11 可见:传统散射直流道有明显涡旋现象,而优化后非直流道内速度分布更为均匀,压力损失较小。
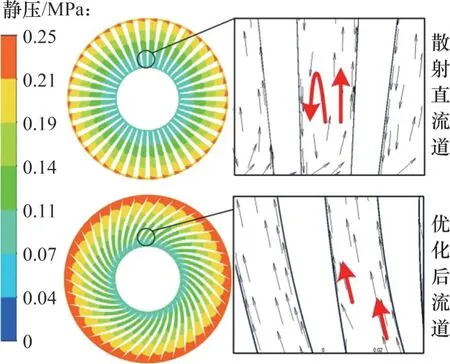
图11 进水面流道速度矢量图与静压云图Fig. 11 Static pressure and velocity cloud map
4.2 轴向换热通道内流动特性
轴向换热通道是冷却水与辊套换热的区域,流道内流体轴向速度的大小反映了水流更新速率的快慢。图12 所示为换热通道内静压与轴向速度对比。从图12可见:3种类型流道的轴向速度均在距离进水面流道端面60 mm 处达到最大值,此处流道内静压为最小值;在0~60 mm 区域内,优化后流道静压下降最多,将压力能转化为流体动能最多;而在其他区域,优化后流道轴向速度始终大于另外2种流道轴向速度,流道换热性能最好。
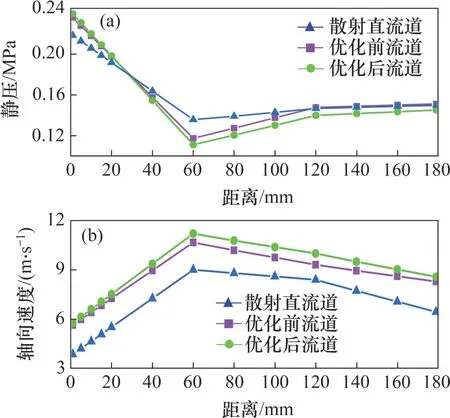
图12 换热通道静压与轴向速度对比Fig. 12 Comparison of static pressure and axial velocity of heat exchanger channel
表6所示为在一定工况下,传统直流道与新型非直流道优化前、后对比结果。由表6可见:相比优化前,优化后冷却辊的流量Q增加5.6%,在换热通道中部(S=90 mm),轴向速度v提升7.07%,进水流道真空度利用率η提升5.1%。相比散射直流道,优化后冷却辊流量Q增大25%,换热通道中部轴向速度v提升21.8%,冷却辊水流更新速率明显提升。
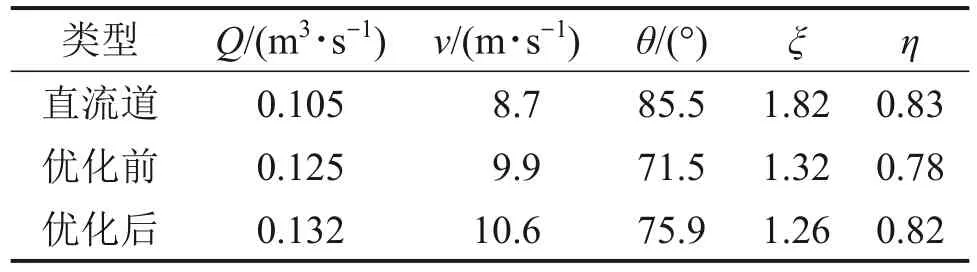
表6 部分性能参数Table 6 Partial performance parameters
5 结论
1) 从流道内流体单元力学分析角度出发可知,进水面采用旋向与冷却辊转向相反的肋道、出水面采用旋向与冷却辊转向相同的肋道可明显减小流道涡旋现象,提高水流更新速率。
2) 基于Bezier 曲线进行参数化建模,采用拉丁超立方抽样克服了数据量大对求解效率的影响,同时采用神经网络与遗传算法相结合的多目标优化方法对非直流道参数进行寻优,具有较高的优化效率。
3) 相比传统散射直流道,在相同工况下,优化后新型差异化非直流道在减少流体涡旋、降低流体冲击的同时,可使出口流量提升25%,换热通道中部的轴向速度提升21.8%,达到强化流道换热、提高水流更新速率的目的。

