问题表征式教学策略研究
夏启明 孟冰清 陆万顺
(宁夏固原第五中学,宁夏 固原 756000)
问题表征是指在头脑中对问题信息进行记载、理解和表达.数学问题表征能力是指使用符号、文字、图表、模型等形式使数学知识与数学问题之间建立一种映射,使复杂的问题变得简单、繁琐的形式变得简化的能力.提高问题表征能力可以有效提高问题解决的效率,因此受到许多学者与教育者的重视.
1 问题表征能力对新高考的重要性
新高考数学命题遵循《普通高中数学课程标准》的基本要求,以数学核心素养为导向,淡化解题技巧,注重学生问题解决的能力,对学生的数学阅读与理解能力提出了更高的要求.许多学生对新高考感到不适应,拿到题目后不知道如何入手,对高考题目感到难以解答,其中一个重要的原因就是学生的问题表征能力不足,学生在答题时不注重理解问题、表征问题.在思维受阻时,不懂得变换表征方式.
1.1 文字表征能力对新高考的重要性
文字表征是通过语言文字来表述信息,对符号、公式等用文字进行解释.学生最初在学习概念或性质时都是通过语言文字的形式,因此文字表征可以帮助学生更快地理解题意,抓住问题的核心.

C.f(-1)=f(4) D.g(-1)=g(2)

1.2 符号表征能力对新高考的重要性
符号表征是把语言、图形进一步抽象为数学符号来理解问题的方式.在运用数学符号进行表征的过程中,学生需要建立数学知识与数学符号之间的联系,深刻理解符号的具体含义[1].借助数学符号通过推理运算等方式解决问题.
例2(2022新高考Ⅰ卷·10)已知函数f(x)=x3-x+1,则( ).
A.f(x)有两个极值点
B.f(x)有三个零点
C.点(0,1)是曲线的对称中心
D.直线y=2x是曲线y=f(x)的切线
分析本题考查函数的极值点、零点、对称性、切线等知识.选项中的信息可以表征为符号语言,然后通过运算验证是否正确.
f(x)有两个极值点,符号表征为f′(x)=0有两个不同的解.
f(x)有三个零点,符号表征为f(x)=0有三个不同的解.
直线y=2x是曲线y=f(x)的切线,符号表征为:满足f′(x)=2的点是否同样满足y=2x.
1.3 图像表征能力对新高考的重要性
图像表征是借助图形来解释信息之间的关系或规律,通过数量关系与图形性质的转化,使思维由抽象转为形象化.高中对于复杂的几何问题通常使用图像表征来使信息更直观化,从而便于发现解题结果或方向.
A.当λ=1时,ΔAB1P的周长为定值
B.当μ=1时,三棱锥P-A1BC的体积为定值


分析本题考查的是空间向量和立体几何.题中正三棱柱通过向量语言,给出了有关点P的信息,需要将它转化为几何条件,绘制图像,数形结合解决问题.
根据题意绘制正三棱柱图像如图1.
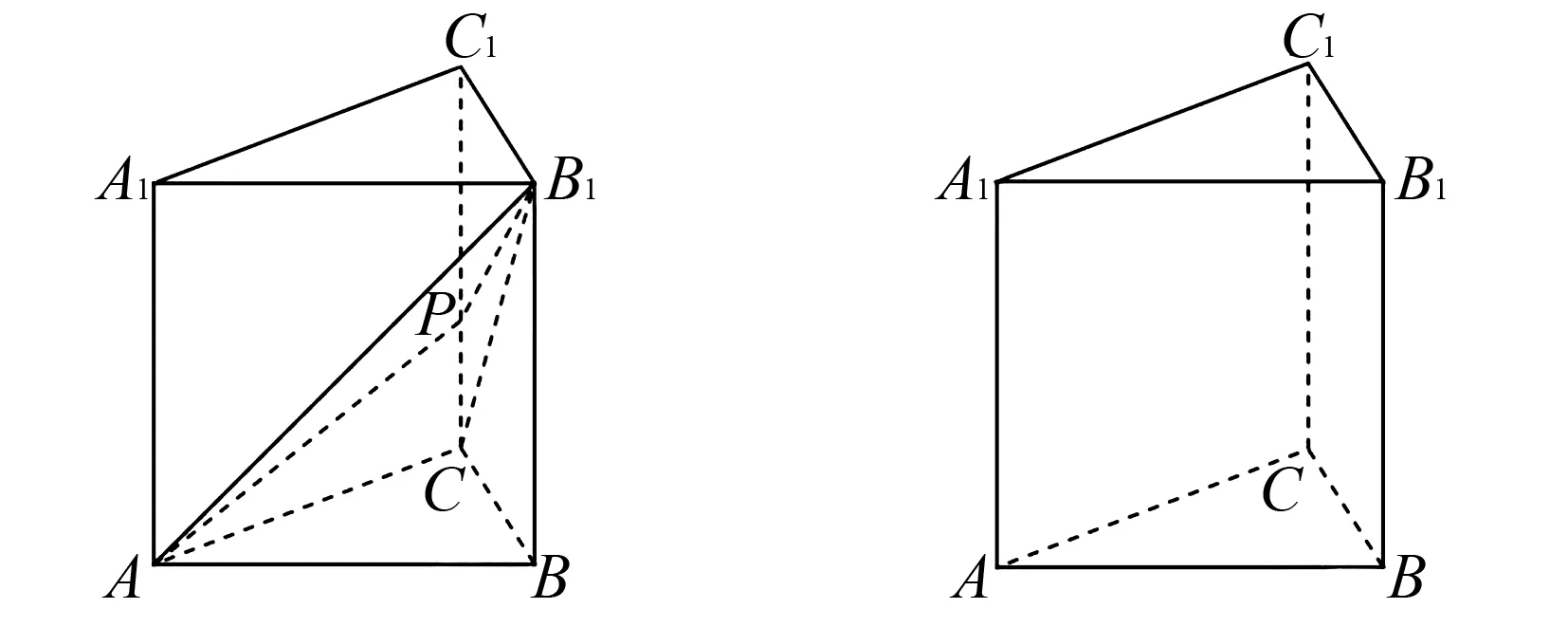
图1 正三棱锥图 图2 选项A表征图
当λ=1时,点P在棱CC1上.图像表征为如图2.
当μ=1时,点P在棱B1C1上,图像表征为如图3.
首先,从审计数据的采集而言,由于随着“互联网+”、云计算的广泛应用,企业的主要业务大都通过信息系统操作得以实现,因此各业务的信息系统中积累了大量的日常管理数据,并以此形成了企业的动态数据源,具有高度的真实性和实效性,也就成为了审计数据采集的源泉。

图3 选项B表征图 图4 选项C表征图

图5 选项D表征图


2 提高问题表征能力的教学策略
2.1 关注一题多解,引导学生从多方面表征问题
在解题教学中,学生不同的表征方式会产生不同的解题思路.不同表征方式的背后代表学生的思维方式的不同.作为教师需要努力的方向就是让学生的思维得到发展,更加趋向于多元化.一题多解就可以很好地训练学生多角度表征问题和思考问题的能力.学生都有自己的擅长表征方式,通过一题多解迫使学生尝试使用自己不擅长的表征方式来表征问题,这就拓宽了学生的解题思路.同时通过多种解题方式的对比,学生可以发现最适宜的表征方式.慢慢地学生运用较弱表征方式的能力也就得到了提高.
一题多解并不表示什么题目都一味地追求多种解法,而是要关注多种解法之间隐藏的思想方法,不同解法之间的内部联系.在教学实践中,许多学生只会模仿例题的解题思路,套用例题的解题步骤,致使思维受阻,问题表征能力弱.教师在教学时,不要急于告诉学生标准的答案,而要让学生自己尝试去表征问题、探索解决问题的方式.在学生思考过后,再从不同角度引导学生表征问题、解决问题.比如题目所说的是什么意思(文字表征)?我们能不能通过引入数学关系式解决呢(符号表征)?根据题目的信息能不能画出图像(图像表征),这样学生就会发现不同表征方式之间的联系与区别,从而提高学生的表征转化意识.
2.2 注重数学知识本质,夯实学生知识基础
数学基础知识是学生运算推理的依据,一切数学问题的解决都离不开基础知识.高考数学的每道考题都是基础知识的升级与变式,因此学生只有掌握基础知识,才能对问题进行精确的表征.但是学生掌握数学知识绝不能靠死记硬背或大量刷题,而是要理解数学知识的本质,理解相关知识之间的区别与联系.这就需要教师在教学时注意挖掘数学知识的本质,帮助学生深入理解知识,让学生知其然更知其所以然.
如何才能更好地帮助学生理解数学知识的本质?首先教师要深入钻研教材,对于知识的由来,推导及证明都要非常熟悉.只有老师自己真正地理解知识才能更好地将知识教给学生.其次在教授基础知识时不要贪图速度,急于将结论告诉学生,应当慢慢引导学生进行推理思考,只有学生自己经过思考得到的知识,对它的理解才会更深刻.最后要注意上下知识之间的联系,帮助学生形成良好的知识体系.
2.3 加强数学阅读训练,帮助学生养成数学表征习惯
新高考涉及了数学文化与生活情境的问题,这类题目就需要学生具备数学阅读能力.传统的教学模式下,许多教师并不认为阅读与数学有多大关系[2].但其实想要学生快速地表征问题,就要培养学生的数学阅读能力.阅读的目的在于理解,通过数学阅读可以促进学生对不同数学语言的理解,学生自己在使用数学语言表征时也会更规范.
在教学时教师要引导学生全面阅读教材内容,找出教材中的重点,正确分析教材的内容.除了阅读教材以外,教师还需要对学生补充有关数学文化或生活情景的数学阅读材料,引导学生分析材料中描述的数学知识,并要求学生对阅读内容采用标符号、列图表、做批注等方式来辅助自己理解内容.
本文以新高考为研究对象,围绕着如何提高学生的问题表征能力展开探讨,这是对目前新高考趋势下改进教学策略的补充,为高中数学教师借助教学有效提高学生的表征能力提供了参考.研究结果主要揭示了三点:一是当前新高考对学生数学问题的表征能力要求很高;二是影响学生数学问题表征能力的因素是多样的;三是教师在教学中要注重提升学生的数学问题表征能力,借助多种方法提升学生的问题表征能力.这要求教师在教学时要立足现实,立足学生,关注当前的教育趋势对培养学生的要求,积极地改进自己的教学策略,践行适应时代的数学教育.

