超短焦投影畸变调校系统设计*
张颜艳,刘 伟,苏文露,郑洪庆
(1.闽南理工学院 工业机器人测控与模具快速制造福建省高校重点实验室,福建 泉州 362000;2.泉州市锐驰智能科技有限公司,福建 泉州 362000)
0 引 言
超短焦投影仪拥有较小的投射比,具有投射距离短、投射画面大、抗光性强等优势,被广泛地应用在数字教学、会议演示、军事指导等领域,满足了“大画面工程设计”需要,极大提升了工程投影室内外应用的“空间场景适应能力”[1,2]。但是,投影仪姿态的变化会导致靠近投影幕布一侧的光线扩散小于较远一侧的光线扩散,投射出来的画面易产生水平或(和)垂直线性畸变[3]。
因此,开发超短焦投影畸变调校系统对提升画面质量和视觉效果具有十分重要的意义。
当前,普通投影仪的画面几何畸变校正受到研究者们的广泛关注。常见的校正方法主要有:
1)艾洛维四角梯形校正法。用户采用遥控器调节画面左上、左下、右上、右下4个顶点的空间位置,实现整个画面调节功能。但调校过程较为繁琐耗时,适用人群有限;且调校精度达不到最佳的画面投影效果[4];
2)机械调节法。王环龙等人[5]提出了一种高精度无感梯形校正模组,通过在投影仪本体底部设置水平角度机构和垂直角度机构,调节投影画面与投影位置呈水平垂直状态和上下垂直状态,保证投射光的中轴线与投影幕布呈90°垂直状态,解决了现有投影仪梯形校正时间长和精度差的问题;但是,该校正模组结构复杂,装配精度难以得到保证;
3)基于摄像头的自动梯形校正法。RAMESH R等人[6-8]提出了预补偿方法,将待投影的图像预先用校正参数进行处理,然后再投影到幕布,实现了校正目的;但是校正参数的获取一般通过投影仪与摄像头、投影墙与摄像头间的几何关系得到,在不允许投影墙设置标志点的特殊情况下,难以获取校正参数。钟波等人[9,10]提出了基于预定图像模板匹配的校正方法,通过对比摄像头实时采集的投影画面与预定图像模板,得出了校正参数;但是,实时采集的投影画面易受环境光照干扰。SUN Ya-qin等人[11]提出了一种基于相位标靶的投影仪畸变校正方法,并在相机畸变的基础上,对获取相位条纹图像进行了研究,利用液晶显示器自显条纹的绝对相位,建立了相位坐标系,对投影畸变进行了测量和预补偿,提高了投影质量和光学测量系统中的测量精度;但是,由于超短焦投影仪的投射比小、水平和垂直视场角远大于普通投影仪,导致摄像头无法精确获取特定图的投影画面,仍存在畸变调校效果不理想等问题。
为了满足企业需求,迫切需要解决投影姿态与画面校正的问题。
笔者以某超短焦投影仪为研究对象,进行投影姿态与畸变画面关系分析、校正算法推导及仿真模拟,并实地搭建调试平台,测试不同姿态变化下的画面智能校正时长和精度,获得可行的高精度智能调校系统,满足高端投影行业对投影姿态提出的自由化要求。
1 理论分析
1.1 投影原理
笔者所研究的投影仪是一款采用数字光处理投影技术的反射式超短焦投影仪,采用数字微镜设备[12](digital micromirror device,DMD)作为光学成像器件,实现数字光学处理过程。
DMD是一种电子输入、光学输出的微机电系统,能够实现高速、高效及可靠的空间光调制,是光机模组的核心器件。每一个DMD都含有最多2×106个独立控制的微镜片,数量与投影画面的分辨率相符[15],在相应的CMOS存储单元上排布成矩阵结构,通过中央处理器控制每个微镜元件的动作,改变入射光的特性,实现所需的空间光调制效果。
超短焦投影仪投影原理如图1所示。

图1 超短焦投影原理
图1中,光源发出的光通过会聚透镜到快速转动的色轮(由红、绿、蓝滤波系统组成),产生红、绿、蓝三基色,由透镜顺序地投射到镶有微镜面阵列的DMD芯片[13,14]表面,微镜面以5 000 Hz的频率转动,反射入射光,经由反射式广角镜头投射出画面,实现可视数字图像投影显示。
1.2 姿态与畸变类型分析
投影仪姿态的变化主要产生的是水平或(和)垂直方向的画面畸变。为了更加全面、客观地评价畸变类型,笔者依据投射比、DMD尺寸、水平/垂直视场角、垂直偏移角等技术参数,得出光源、DMD和投影画面之间的几何关系,建立兼顾水平左右转动、垂直俯仰转动作业状态下的畸变区域特征点识别模型;通过改变投影仪位姿信息,可获取畸变画面所有类型。
典型畸变画面类型如图2所示。

图2 畸变画面
通过畸变类型分析,校正情况有8种,分别是:左转投影、右转投影、仰视投影、俯视投影、左转+仰视投影、左转+俯视投影、右转+仰视投影和右转+俯视投影。综合考虑视场角、偏移角、可接受校正可视尺寸等因素,可得出临界校正角度分别为:水平±15°、垂直上倾5°和垂直下倾30°。
1.3 校正方案
从光路原理分析,投影仪放置角度偏差导致的画面畸变,属于大像差系统问题,不需考虑衍射影响;同时,考虑校正后的画面在原投影范围内,不会产生新的像差。
基于几何光学原理,可采用的校正方案有两种,分别是机械法和解析法。
校正方案对比如表1所示。

表1 机械法和解析法对比
由于解析法校正响应快、成本低、校正灵活,此处笔者采用解析法。
超短焦投影校正原理如图3所示。
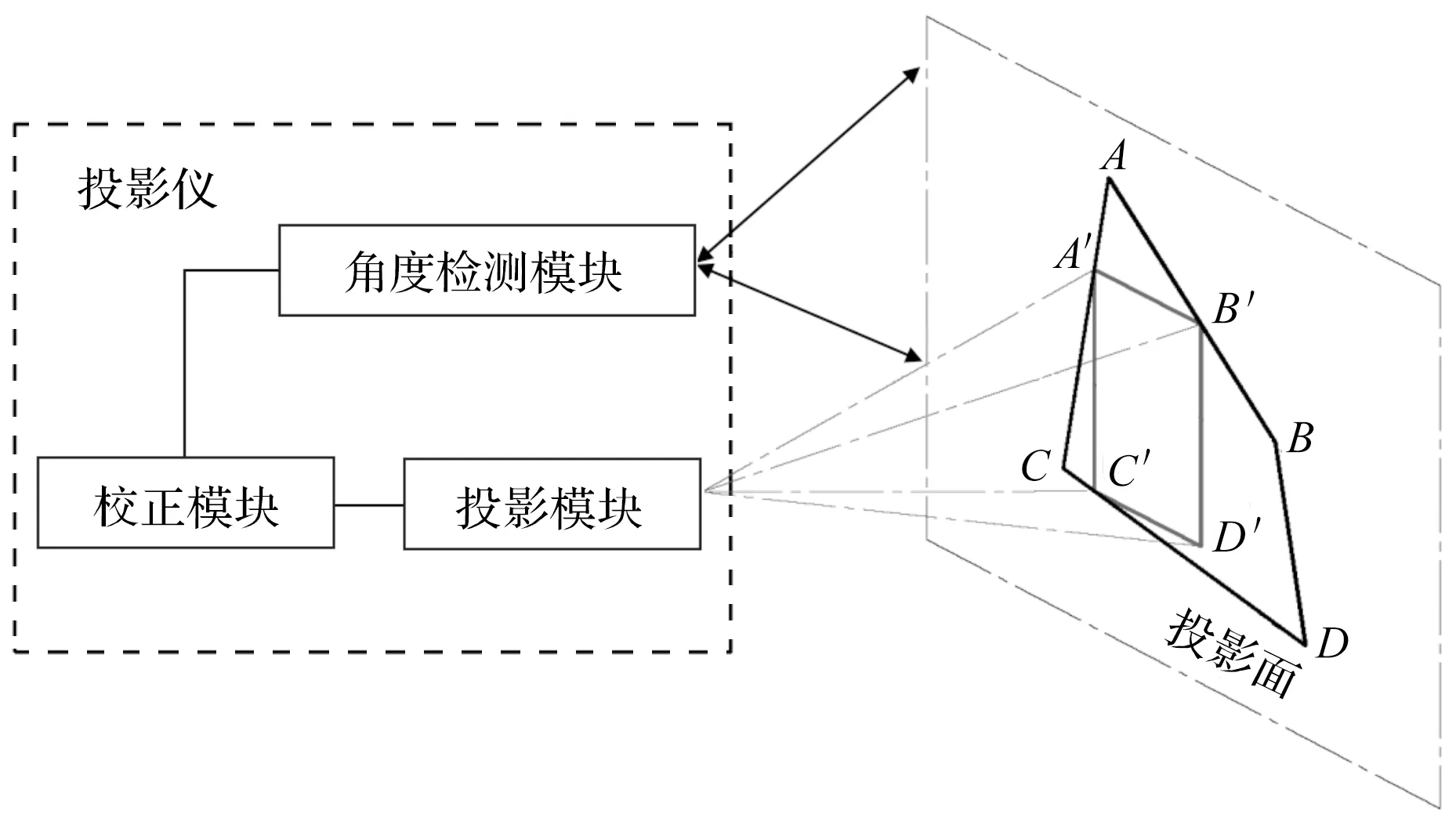
图3 超短焦投影校正原理
图3中:标定好的角度检测模块实时监测投影仪的姿态情况,输出投影仪水平和垂直倾斜角度给校正模块;校正模块利用倾斜角度和投影模型,确定畸变区域顶点信息(图3中的A点、B点、C点和D点),基于搜索算法获取最优校正区域顶点信息(图3中A′点、B′点、C′点和D′点),进而获取DMD芯片实际工作区域的新顶点坐标信息,改变空间光调制器矩阵,与光轴倾斜产生的畸变相抵消。
投影模块投射出校正后的画面A′B′C′D′,在投影区域中显示为规则的矩形画面。
2 投影姿态信息获取
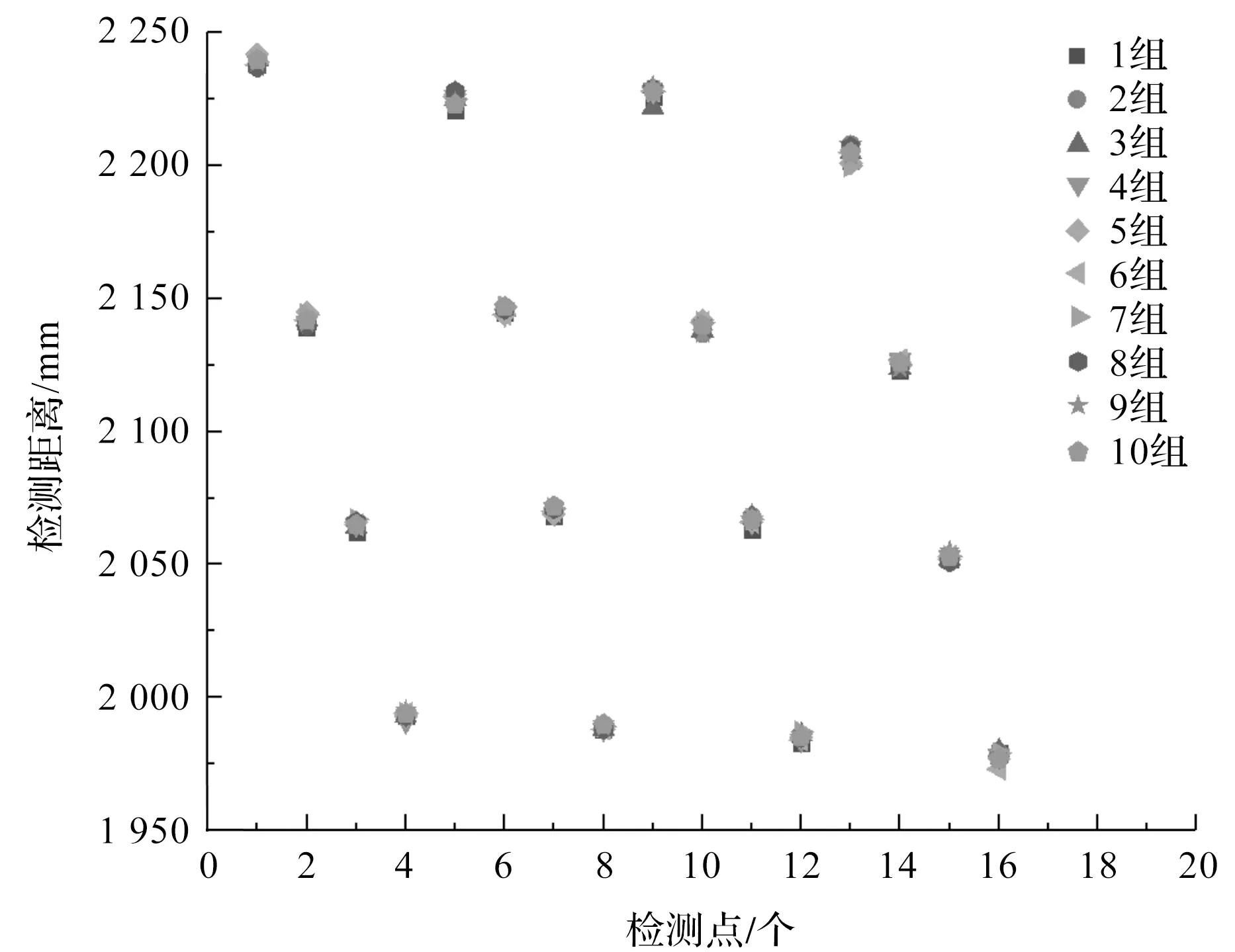
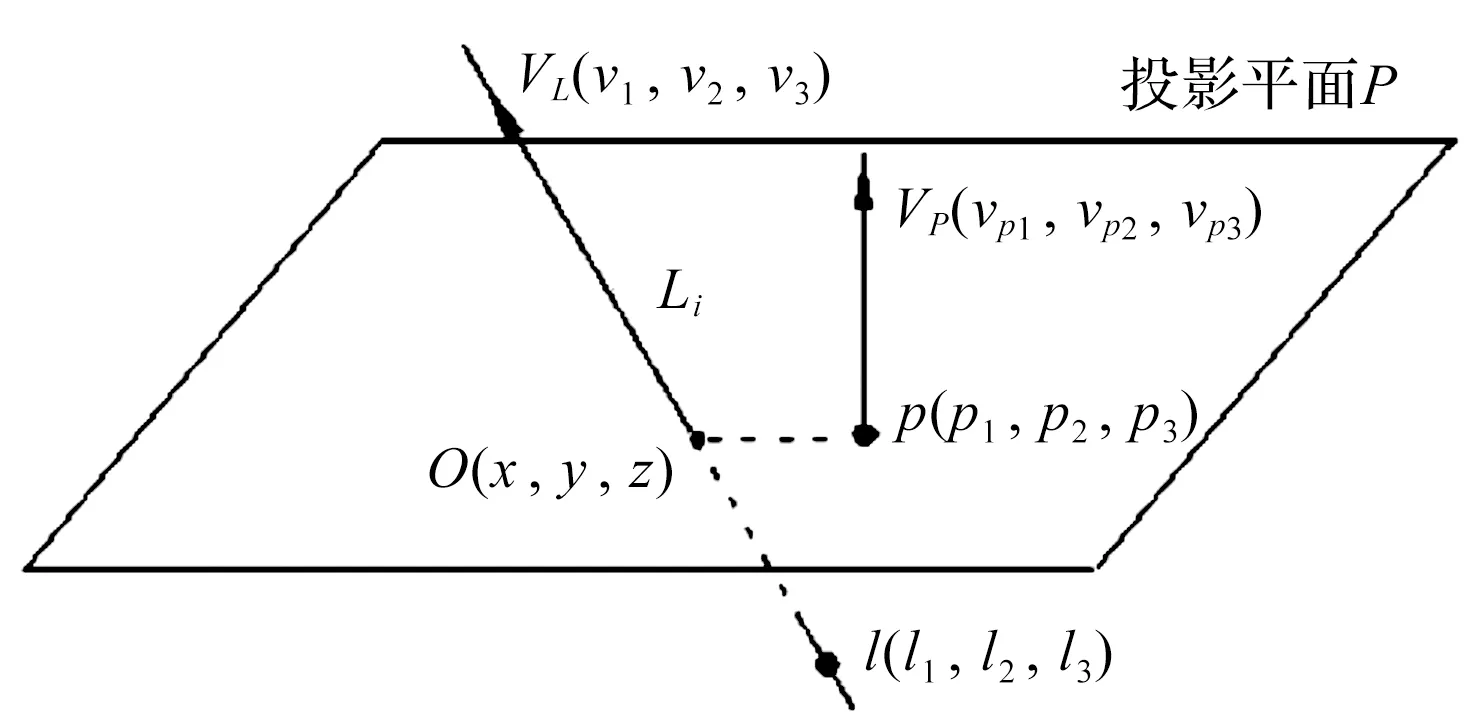
飞行时间多区域测距(time of flight,TOF)系统采用的是VL53L5CX传感器。它能直接测量时间来对应距离。测距的主要原理是,通过单光子雪崩二极管接收光子产生相应电流,由时间数字转换器来计算时间。经过N次的发射与接收,时间数字转换器能够记录n次(n TOF系统视场描述和4×4工作模式下的区域映射关系如图4所示。 图4 系统视场描述和4×4区域映射 根据图4描述可知,TOF系统水平视场角为45°、垂直视场角为45°、对角视场角为63°。4×4模式下视场区域映射图中的数值代表的是16个距离检测点,可输出检测范围内16个原始距离数据。 为了保证距离数据稳定性,笔者选择1次采集10组距离数据进行分析。 16个检测点的10组距离值如图5所示。 图5 检测距离数据 由图5可知,不同检测点的10组数据的差值体现了测距的稳定性。通过方差分析发现,4×4模式下测距误差≤±5%。 投影姿态信息获取的关键是拟合三维空间散点,找到检测平面。笔者采用误差函数的极小值点法。设A、B、C为平面的最优参数,对于不过原点的平面方程为Ax+By+Cz+1=0。将16个检测点的10组空间坐标代入平面方程中存在误差,所有误差的平方和函数表达式如下式所示: (1) 式中:ei为检测点到平面误差,mm;(xi,yi,zi)为检测点空间坐标,mm,i=1,2,……160。 误差的平方和函数为A、B、C的函数,是4维空间中的1个下凸超平面,具有唯一极小值,也是全局最小值。 笔者利用误差的平方和函数对A、B、C的一阶偏导为0,经整理可得: (2) 将式(2)简化为三元一次方程组,求解可得A、B、C的值,得出拟合平面方程。 三元一次方程组如下: (3) 其中: (4) 对于投影仪偏移角度数据还需完成初始位置正面标定。 首先将投影仪摆正(可用水平仪查看),在投影幕布上投射出1个标准矩形;再利用TOF系统的传感器视场角度和16个检测点到拟合平面的距离信息,获取投影仪与投影面法线夹角θ,此时进行正面零位标定。如果光机偏移角度过大、检测区域有异物或是贴有不同反射率的材料,点到拟合平面的距离数据会大于60 mm,检测点所测距离数据在角度计算时为无效数据,对其进行拦截。 顶点信息的获取需要借助空间投影平面和投影光线方程。根据投影仪特定的透射比、光源、分辨率等参数,笔者建立空间投影平面方程(即由光源和DMD顶点坐标,建立空间投影光线方程)。如果投影光线与投影平面不平行,将存在交点,即畸变画面的顶点[16,17]。 空间投影光线与投影平面的交点如图6所示。 图6 投影平面与投影光线 图6中,光线Li过点l(l1,l2,l3),方向向量为VL(v1,v2,v3),则光线方程的参数形式如下: x=l1+v1t;y=l2+v2t;z=l3+v3t (5) 投影平面P过点p(p1,p2,p3),其法线向量为Vp(vp1,vp2,vp3),则平面方程的点法式形式如下式所示: vp1(x-p1)+vp2(y-p2)+vp3(z-p3)=0 (6) 投影光线和投影平面的交点O(x,y,z)将同时满足式(5)、式(6),可联立求解得出参数表达式,如下式所示: t=[(p1-l1)vp1+(p2-l2)vp2+(p3-l3)vp3]/f (7) 其中: f=v1vp1+v2vp2+v3vp3 (8) 当f=0时,表示光线与投影平面平行,投影幕布上没有投影画面,所以此处的f≠0。 联立式(5)、式(7)、式(8),求解出畸变画面的顶点位置坐标(x,y,z),位置坐标计算公式如下: (9) 搜索算法是利用计算机的高性能,有目的地根据初始条件和扩展规则,穷举一个问题解空间的所有可能情况,寻找符合目标状态的节点,从而求出问题解的一种方法。 典型的畸变画面搜索方向如图7所示。 图7 搜索方向 针对图7中畸变画面特点,笔者确定搜索基点、搜索方向(e1为水平方向,e2为垂直方向,即按十字方向搜索)、搜索步长δ(δ≥1,合理的选择与全局搜索能力密切相关)和终止条件(按照画面比例16/9进行设置)。当搜索进行到终止条件时,以最后的搜索基点作为校正画面的左上顶点,依次得出另外3个顶点坐标。 搜索具体步骤为: 1)选择AC中点作为搜索基点B(k),B(k)=(i(k),j(k))。令k=1,投影区域内的点集为Rn,则B(k)∈Rn。AC直线方程为y=f1(x),AB直线方程为y=f2(x),CD直线方程为y=f3(x); e2方向:若j(k)>f3(i),则j(k):=j(k)+δ(δ≥1,扩大搜索范围),k:=k+1;否则停止搜索迭代,令j=j(k); 笔者以校正画面的4个顶点和光源坐标,建立4条直线方程,求解出直线与DMD平面的交点位置坐标,即为DMD芯片新顶点。 具体算法流程,即DMD新顶点信息获取流程如图8所示。 图8 DMD新顶点信息获取 根据企业对投影畸变校正精度及响应等具体需求,笔者将投影仪的主要参数(水平视场角131.34°,垂直视场角46.02°,垂直偏移角25.32°,投射比0.23,DMD工作面尺寸5.184 mm×2.916 mm,光心与幕布距离400.4 mm)代入校正系统,正投时可得到80″投影画面;通过改变投影仪放置姿态,对校正前后画面进行仿真研究。 4种典型姿态变化产生的畸变画面和校正画面如图9所示。 图9 畸变画面校正仿真 仿真结果表明:调校系统校正后的画面是1个16∶9的标准矩形画面,解决了因投影仪水平和垂直姿态组合改变引起的画面畸变问题,符合视感效果要求。当投影仪校正范围为水平±15°、垂直下倾15°时,DMD利用率大于20%,屏幕显示尺寸大于57″,可以实现最优校正,达到用户可接受范围。 为了进一步验证智能调校系统的可行性及校正效果,笔者搭建了实验平台(调试平台)。 实验平台(调试平台)的实物图如图10所示。 图10 实验平台(调试平台) 图10(a)为笔者自主研发的校验设备,用于准确改变投影仪水平-垂直位姿,以验证校正算法的准确性;图10(b)为笔者搭建的暗室环境,用于整机设备调校。 接下来需要按照校准算法,编写工具类代码。在软件系统中,笔者创建1个相对应的类对象,将TOF系统测得的投影仪姿态偏转角度,采用对象调用方法,计算出标准矩形校正画面所对应的DMD顶点坐标。笔者对装有调校系统的超短焦投影仪进行8种典型畸变调校。 整机调试主要数据如表2所示。 表2 整机调试数据 由表2可知:不同放置姿态作业下,DMD的顶点坐标和投影画面尺寸不同,调校画面角度偏差≤0.1°,整机调校时长≤2 s,相对于普通投影仪,基于摄像头的智能校正技术的速度快3倍。 笔者将调校好的投影仪放在家用床头柜进行应用,并改变其放置姿态。当投影仪发生水平向右移动和垂直向下倾斜时,投影画面为不规则的四边形,几何畸变严重。 投影画面校正前后对比图如图11所示。 图11 校正前后投影画面 `图11中,智能调校系统能够根据TOF系统输出的实测偏移角度,在1.173 s内快速实现畸变画面自校正,校正好的画面如图11(b)所示。 案例表明,该系统能够有效抵消超短焦投影仪放置姿态变化所造成的画面畸变。 针对超短焦投影畸变问题,笔者提出了一种高精度超短焦投影畸变智能调校系统,采用软件仿真及实验平台,验证了调校系统的可行性,实现了对输入视频投影图像几何畸变进行快速、精准校正的目的。 主要研究结论如下: 1)该智能调校系统调节精准、效率高。通过研究不同旋转角度状态下的投影区域畸变规律,利用搜索算法获取了最大16∶9矩形校正画面,反推计算获得了DMD四顶点坐标。8种不同投影畸变智能校正响应时间2 s内完成,畸变角度偏差可控制到小数点后两位,校正精度和效率高; 2)校正角度范围广。80″投影画面调校实验表明:当投影仪倾斜角度过大,如“水平转动15°+垂直下倾15°”,智能校正后的显示尺寸仍能达到57.1″,且视频显示清晰度较高,能够较好地满足大部分用户需求。 目前,笔者主要解决了超短焦投影仪水平或(和)垂直姿态变化下的畸变问题。在后续的研究工作中,笔者将在当前校正方法基础上,开展针对不同投射比的投影仪畸变画面智能校正,以及放置姿态倾斜下投影仪畸变画面的校正。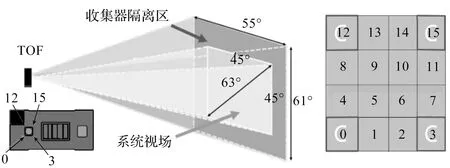
3 畸变校正核心算法
3.1 畸变区域顶点信息获取算法
3.2 最优校正投影区域搜索算法

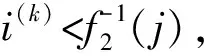
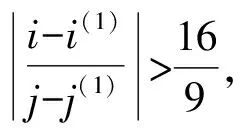
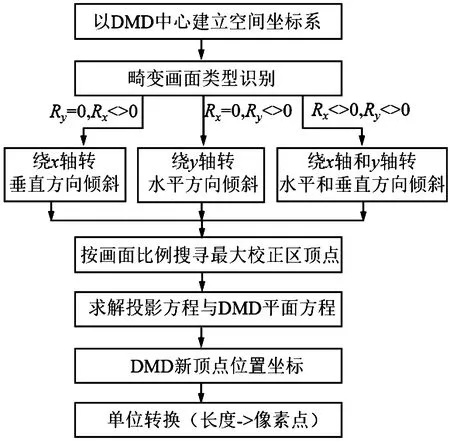
3.3 DMD顶点位置信息获取算法
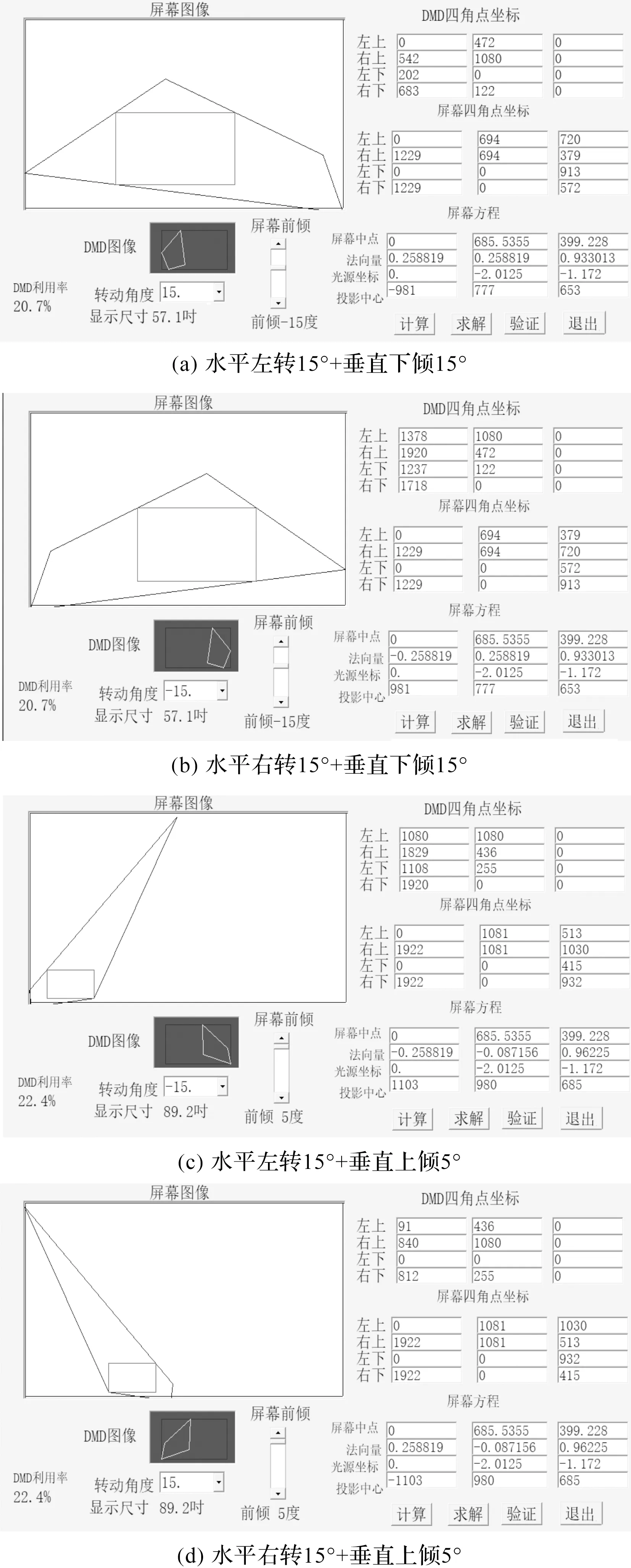
4 仿真分析
5 实验与结果分析



6 结束语

