章动式双圆弧螺旋锥齿轮齿面曲率与运动特性研究*

曾 益,潘 伶,尹志强,张 俊

(福州大学 机械工程及自动化学院,福建 福州 350108)

0 引 言

章动式双圆弧锥齿轮是一种将双圆弧锥齿轮应用在章动传动上的新型齿轮,它同时具备双圆弧齿廓高承载、易润滑的特性以及章动传动结构紧凑和大传动比的优点,在精密减速器领域拥有广阔的应用前景。

内啮合锥齿轮是章动齿轮传动机构的关键部件,其齿轮副的传动性能主要由锥齿轮的齿廓形状决定[1]。相较于传统的渐开线齿廓,双圆弧齿廓采用两对凸、凹齿面相啮合的传动方案,极大提高了齿面的接触强度,因此受到了国内外学者的广泛关注。

李进宝[2]从共轭齿面形成原理出发,基于加工机床和刀具参数,推导了双圆弧弧齿锥齿轮的齿面方程,简要分析了啮合齿面的两种曲面类型。姚俊红等人[3]进行了双圆弧弧齿锥齿轮的实体建模及动态啮合模拟,分析了不同参数和误差对齿面几何形态的影响。LITVIN F L等人[4]对双圆弧斜齿轮进行了齿面接触分析(TCA),确定了啮合齿面上的接触迹线,并根据接触点的曲率参数,得到了接触椭圆的尺寸和方向。ZHANG Rui-liang等人[5]运用TCA方法研究了双圆弧弧齿锥齿轮的啮合传动特性,发现了其理论分析结果在一定程度上与试验相符。WEN L等人[6]对9种不同横向压力角组合的双圆弧斜齿轮进行了啮合仿真,有限元结果表明,最佳压力角能有效降低齿轮圆角处的最大弯曲应力。

上述文献研究的双圆弧齿轮传动形式是外啮合传动,该传动方式的应用目前已相当成熟;但由于复杂的齿轮空间结构和齿轮副难以展成加工等原因,内啮合传动研究进展缓慢。

目前,内啮合传动主要有两个研究方向:1)双圆弧谐波齿轮传动;2)双圆弧锥齿轮章动传动。前者聚焦于公切线式双圆弧齿廓参数的优化设计,促使谐波齿轮获得更好的啮合性能[7,8];后者采用标准分阶式双圆弧齿形作为锥齿轮的基本齿廓,在三维精确建模、有限元仿真和样机试验方面取得了一定的进展[1,9,10]。

需要指出的是,尽管笔者课题组前期已采用有限元法得到了章动式双圆弧锥齿轮的齿面接触区分布,但缺乏理论计算角度的分析,因此,还需要对齿面接触点的曲率参数进行系统推导。

而诱导法曲率、相对运动速度和滑滚比是评价齿轮传动性能的重要指标,同时也是齿轮弹流润滑分析和齿面磨损研究中的重要影响因素;这些参数无法采用有限元法获得,因此,有必要从理论层面对章动式双圆弧锥齿轮在啮合过程中的曲率变化和运动特性进行深入研究。

笔者拟在通用齿面数学模型的基础上,开展内啮合双圆弧螺旋锥齿轮章动传动齿面接触分析(TCA),研究其在无安装误差下的接触轨迹;根据微分几何理论,分析各接触点处曲率的变化趋势和相对运动情况;最后分析齿面接触区域,以期为后续研究奠定基础。

1 齿面数学模型的建立

笔者课题组前期已经成功建立章动内、外锥齿轮的通用齿面参数模型[11]。

其主要建模思想为:根据共轭齿廓互为包络线的原理,可以由一个假想的冕齿轮得到内、外锥齿轮齿面;可将标准双圆弧齿形沿实际齿向线扫掠,生成冕齿轮的基本齿廓曲面。

GB/T 12759—1991标准规定的基本齿形,标准双圆弧齿形,如图1所示。

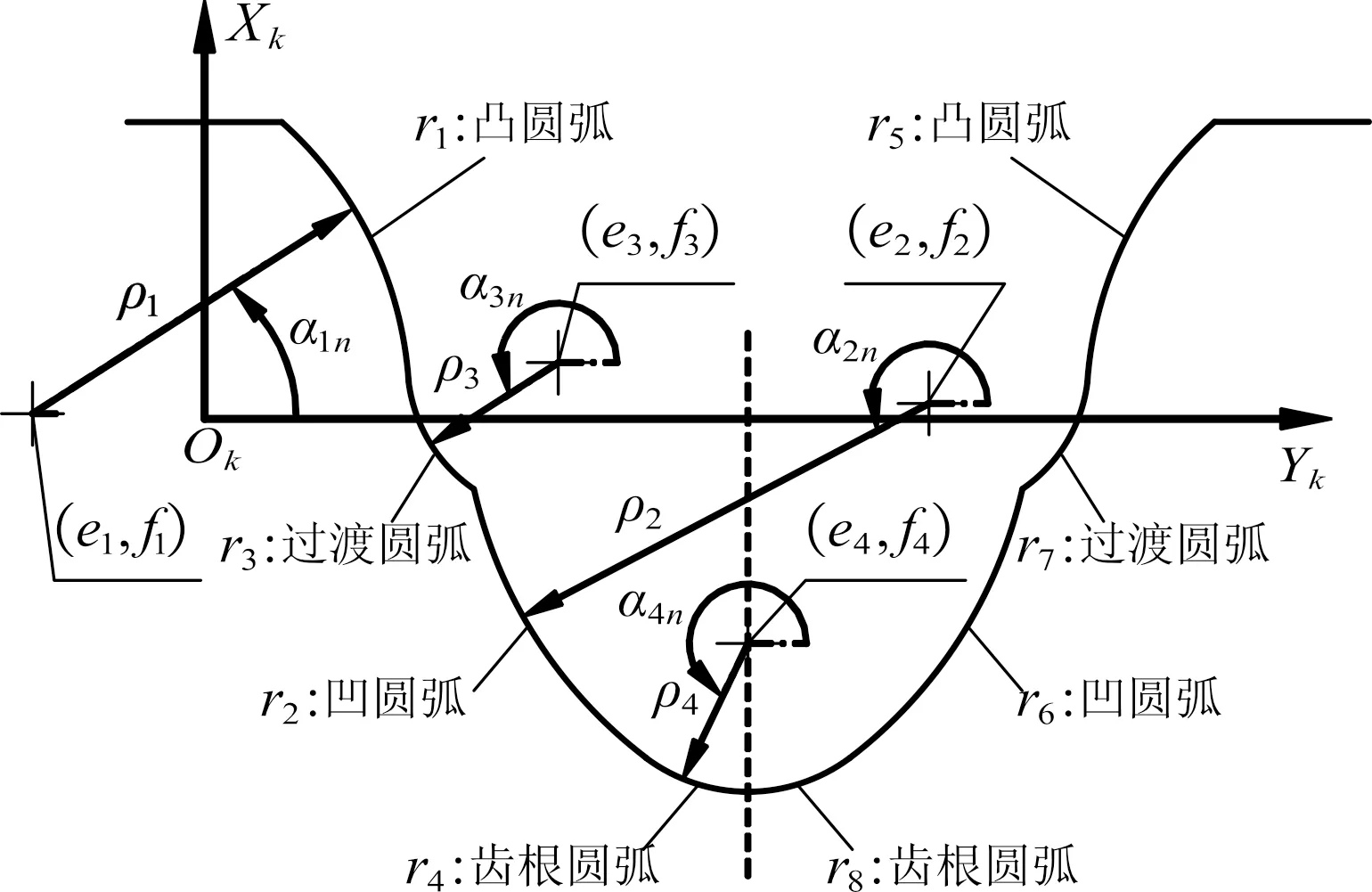
图1 标准双圆弧齿形

标准双圆弧齿形分别由凸圆弧、过渡圆弧、凹圆弧和齿根圆弧组成。为明晰各段圆弧的位置关系,笔者在图1中建立直角坐标系Sk(OkXkYkZk)。

在该直角坐标系中,Xk轴位于齿厚的对称线上,Yk轴位于齿形的节线上,则第j(1～8)段圆弧上任意点n的坐标在坐标系Sk中可表示为:

(1)

式中:(ej,fj)为第j段圆弧的圆心坐标;ρj为第j段圆弧的圆弧半径;αjn为第j段圆弧上点n的向径同Yk轴正向的夹角(定义逆时针方向为正)。

笔者选用对数螺旋线作为冕齿轮的公称齿向线,可保证线上各点的螺旋角β不变。在此基础上,为使齿廓符合等强度原则,笔者需调整公称齿向线,以获得实际齿向线。

齿向线调整示意图如图2所示。

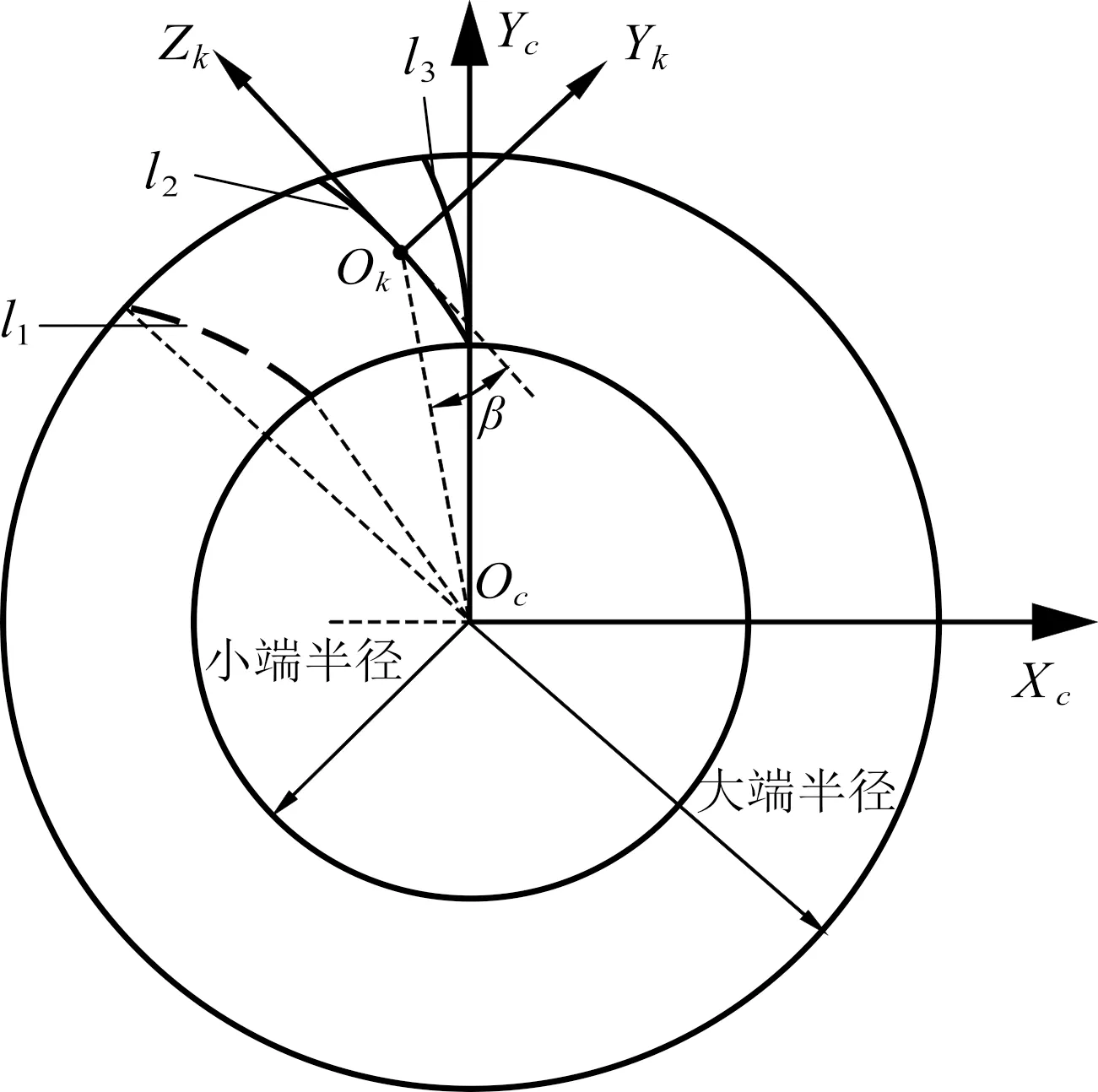
图2 齿向线调整示意图

图2中,l1为公称齿向线,可用极坐标方程ρ(θ)=eθcotβ来描述;l2和l3分别为调整后的左、右实际齿向线。

齿向线在冕齿轮节锥面坐标系Sc(OcXcYcZc)中可表示为:

(2)

式中:∓为-代表左齿廓,+代表右齿廓;su为齿厚(槽)宽,u=1表示凸圆弧齿厚宽,u=2表示凹圆弧齿槽宽;Δθe为调整过程中的转角。

笔者将双圆弧齿形分别沿左、右实际齿向线扫掠,即可得到冕齿轮在坐标系Sc中的齿面方程:

(3)

笔者建立内锥齿轮、外锥齿轮和冕齿轮的啮合坐标系,利用空间啮合原理对冕齿轮齿面方程进行坐标变换,推导出内、外锥齿轮的曲面族参数方程:

(4)

式(4)中的曲面族方程rpi由齿向线参数θi、齿形参数αijn和冕齿轮啮合转角参数φc共同确定。

根据齿轮啮合原理,内、外锥齿轮的齿面参数方程还需满足如下啮合方程:

nc·vci=0

(5)

式中:nc为冕齿轮齿面的单位法矢;vci为冕齿轮与锥齿轮在啮合点的相对速度矢量。

整理式(5)后,可得到参数φc(θi,αijn)的表达式。

至此,内、外锥齿轮齿面方程经过简化,由双参数θi和αijn统一表示如下:

(6)

2 章动式双圆弧螺旋锥齿轮TCA

螺旋锥齿轮齿面属于点接触共轭曲面,在无载或轻载情况下,相互啮合的齿面间理论上只形成一个瞬时接触点。随着传动的进行,各瞬时接触点的轨迹构成一条接触迹线。双圆弧齿廓同一轮齿侧面在啮合过程中会出现双点接触,因此,存在上、下两条接触迹线。

笔者采用TCA方法来确定这两条接触迹线。

章动齿轮传动本质上是一种锥齿轮少齿差行星传动,常见的单级锥齿轮章动传动往往由固定的内锥齿轮和同时作自转与摆动运动的外锥齿轮组成。因此,在进行TCA前,笔者需根据相对运动原理将周转轮系转化为定轴轮系,此时可认为内、外锥齿轮只绕自身轴线转动。

根据这一原理,笔者建立内、外锥齿轮章动传动啮合坐标系,如图3所示。

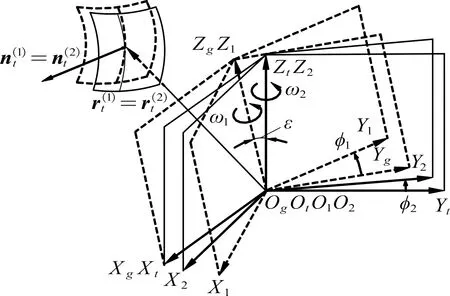
图3 章动齿轮传动啮合坐标系

在不考虑装配误差的情况下,笔者分别引入内、外锥齿轮的固定坐标系St(OtXtYtZt)和Sg(OgXgYgZg),用以描述两者的相对运动关系。其中,旋转坐标系S2和S1仍固连在对应齿轮上,各坐标原点与节锥顶点重合。啮合过程中,外锥齿轮从起始位置Sg绕Z1轴旋转φ1角度到达S1,内锥齿轮从起始位置St绕Z2轴旋转φ2角度到达S2。

假设St为全局固定坐标系,则此时内、外锥齿轮齿面接触点的径矢和单位法矢在St坐标系中表示如下:

(7)

其中,

(8)

(9)

(10)

(11)

式中:ni为锥齿轮齿面单位法矢,对于凸齿面,其方向是由空域指向实体,对于凹齿面则相反。

啮合过程中的齿轮副要想连续相切接触,必须满足一个条件,即在某一固定坐标系下,两齿面瞬时公共接触点处的位置径矢rt和单位法矢nt相等[12],即:

(12)

在理论上,所有接触点中存在一个计算初始点,使得齿轮副在该点处满足瞬时传动比等于理论传动比,通常该点位于啮合齿面的中点附近。因此,首先要根据齿面旋转投影关系构造非线性方程组,求解得到外锥齿轮初始点的齿面参数θ1和α1jn,进而利用传动比关系以及式(12),确定剩余的4个参数。

以其中的内锥齿面参数φ2作为已知输入量,方程组在每次迭代前,需要通过给定步长Δφ2对φ2值进行改变,将新的φ2代入式(12),去计算其余5个参数的一系列解,直到接触点超出齿面边界时,迭代停止。

3 齿面接触点曲率及运动参数计算

啮合齿轮副共轭齿面之间的曲率和相对运动直接影响着齿面的接触区尺寸、摩擦学性能和接触强度。因此,笔者根据已推导的齿面方程和求解得到的接触点参数,采用微分几何,详细推导接触点处各类曲率参数和运动参数表达式。

3.1 齿面曲率计算

由梅尼埃(Meusnier)定理可知,齿面上一点沿任意方向的法曲率可表示为:

(13)

式中:E,F,G为曲面第一基本齐式系数;L,M,N为曲面第二基本齐式系数。

第一、第二基本齐式系数可表示为:

(14)

法曲率反映了曲面定点在不同方向上的弯曲程度,当定点参数确定时,法曲率只与选择的切线方向有关。所有切线方向中存在一对互相垂直的主方向,使得对应主曲率为法曲率中的最大值和最小值。

笔者引入λ=dαijn/dθi表征切线方向,令dk/dλ=0,可得主方向和主曲率的计算公式[13]为:

(15)

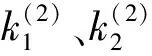
需要说明的是,计算得到的主方向1和主方向2实际上与齿廓方向和齿线方向区别不大,因此,笔者在以下的分析中将采用后者进行表述。

实际啮合接触的齿轮副表面由于受到工作载荷影响会产生弹性变形,形成以接触点为中心的接触椭圆,其长轴方向为诱导法曲率绝对值最小的方向,短轴方向为诱导法曲率绝对值最大的方向。

接触椭圆和主方向的位置关系如图4所示。

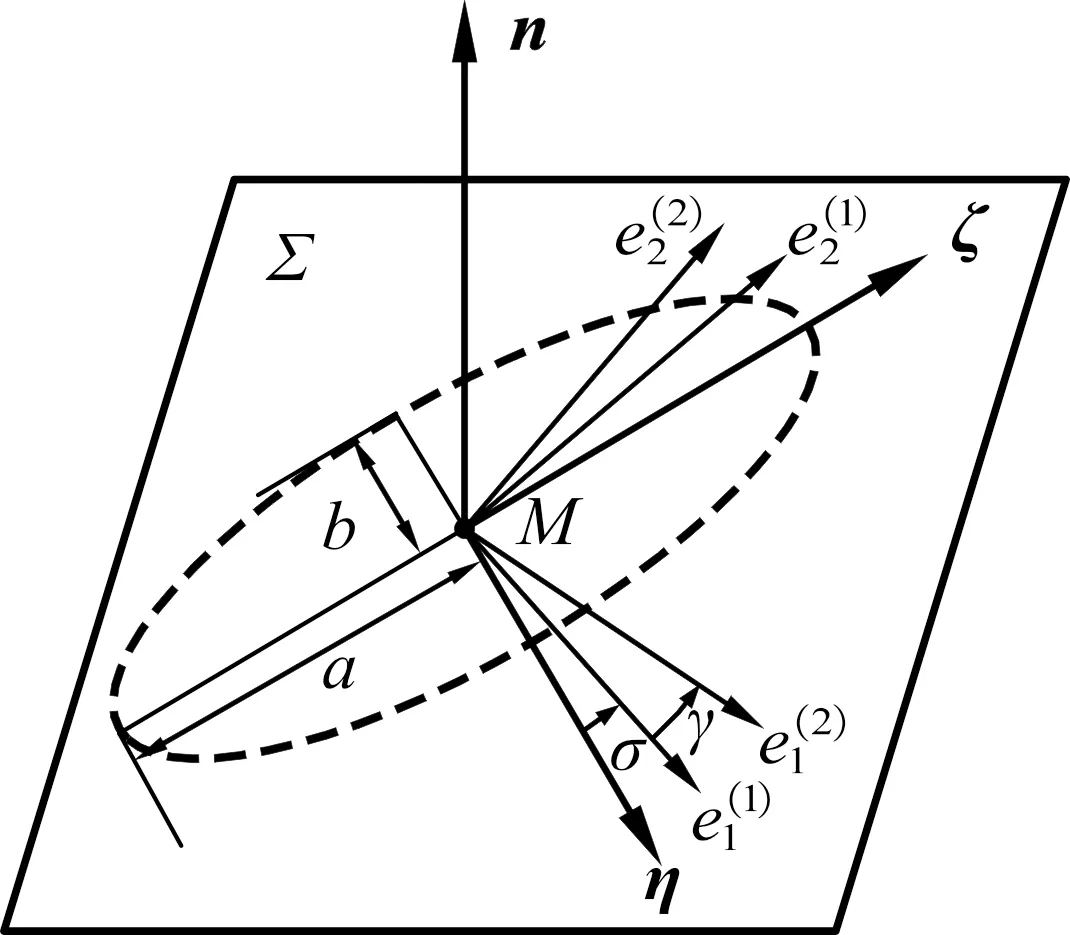
图4 瞬时接触椭圆和主方向

图4中,齿轮副在接触点M处具有共同的法矢n和切平面∑,主方向和椭圆长短轴方向的位置关系由夹角σ和γ确定。

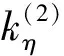
(16)

而短轴η方向的诱导法曲率为该方向的法曲率之差,可表示为:

(17)

式中:

(18)

根据定义,长短轴方向的诱导法曲率为极值,故令dkη/dσ=0,即可求出σ:

(19)

同理,可得长轴ζ方向的诱导法曲率Δkζ。

笔者根据Hertz弹性接触理论,采用下式计算瞬时接触椭圆的长短半轴a和b,即:

(20)

式中:w为载荷;E为当量弹性模量;δa,δb为计算参数,具体取值参照文献[14]。

其中:A=(Δkη+Δkζ)/2。

上述所求的长短半轴a和b都是在公共切平面内的,还需将其投影到齿轮的轴截面,以便在齿面坐标系中进行表示[15]。

3.2 齿轮副运动参数计算

(21)

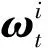
(22)

其中,长、短半轴方向的单位矢量ζ、η可根据图4得到,即:

(23)

各运动速度关系如图5所示。

可得到接触点处卷吸速度Ue和相对滑动速度Us的矢量表达式:

(24)

速度矢量与椭圆长轴之间的夹角θe和θs为:

(25)

进而得到滑滚比S的计算公式为:

(26)

4 算例与分析

齿轮副的基本设计参数如表1所示。

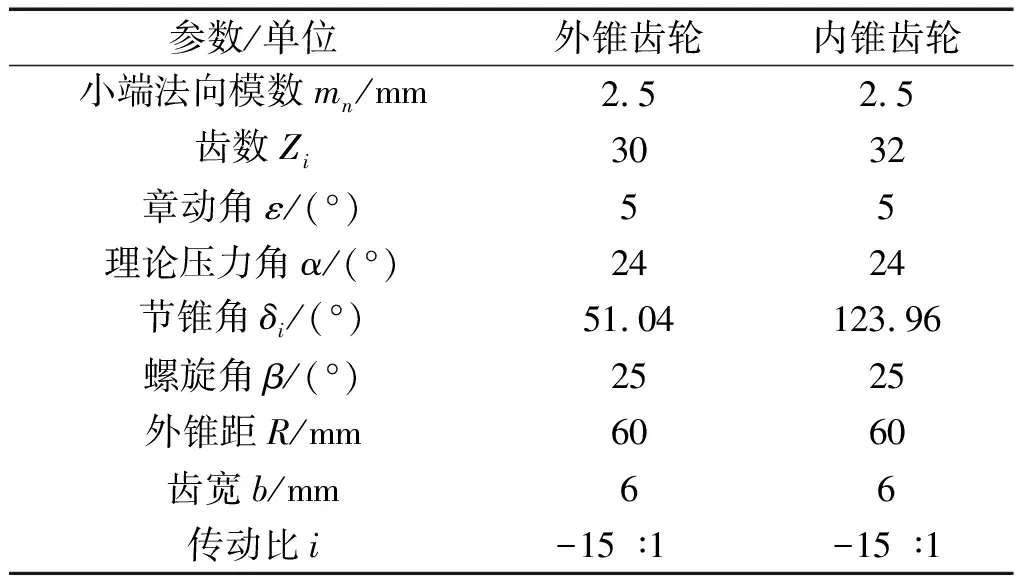
表1 齿轮副基本参数

其设计参考值满足输出扭矩M=100 N·m,输入转速为1 000 r/min～1 500 r/min。

章动式双圆弧螺旋锥齿轮的实体样机如图6所示。

图6 章动式双圆弧螺旋锥齿轮样机

左、右实际齿向线并不相同,因此轮齿左、右侧齿面的空间曲面结构存在一定差异。笔者利用MATLAB软件对上述理论计算进行编程求解,因篇幅所限,仅就外锥轮齿右侧齿面与内锥轮齿左侧齿面啮合的计算结果展开分析。

4.1 齿轮接触特性分析

外锥轮齿右侧齿面瞬时接触点的分布情况如图7所示。

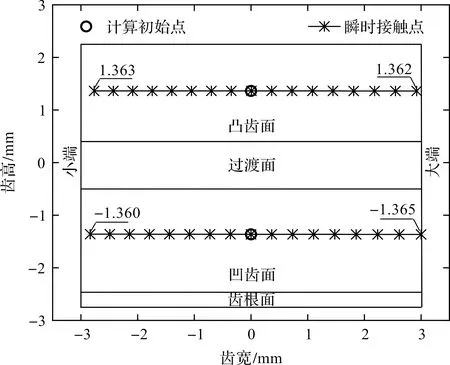
图7 外锥齿轮齿面瞬时接触点轨迹

在齿轮传动中,由于凸、凹齿面先后参与啮合接触,均匀选取各自齿面上的17个接触点,即构成图7上、下两条接触迹线。同齿面的接触点都是沿着齿宽方向由一端向另一端移动,且啮入点与啮出点在齿高方向的偏移量较小,基本处在计算初始点所确定的齿宽线上。

此外,凸、凹齿面接触点对应的压力角分别为23.0±0.02°和24.9±0.05°,同理论压力角24.0°接近,表明齿轮副在传动过程中具有良好的接触状态。

由于笔者采用标准双圆弧齿形作为锥齿轮的基本齿廓,当模数一定时,齿形的其他参数也被确定下来。而不同的模数下齿形尺寸的差别较大,无法放在统一的尺度下进行比较,因此,笔者针对描述齿向线的螺旋角参数进行影响因素分析。

不同螺旋角对接触迹线的影响如图8所示。

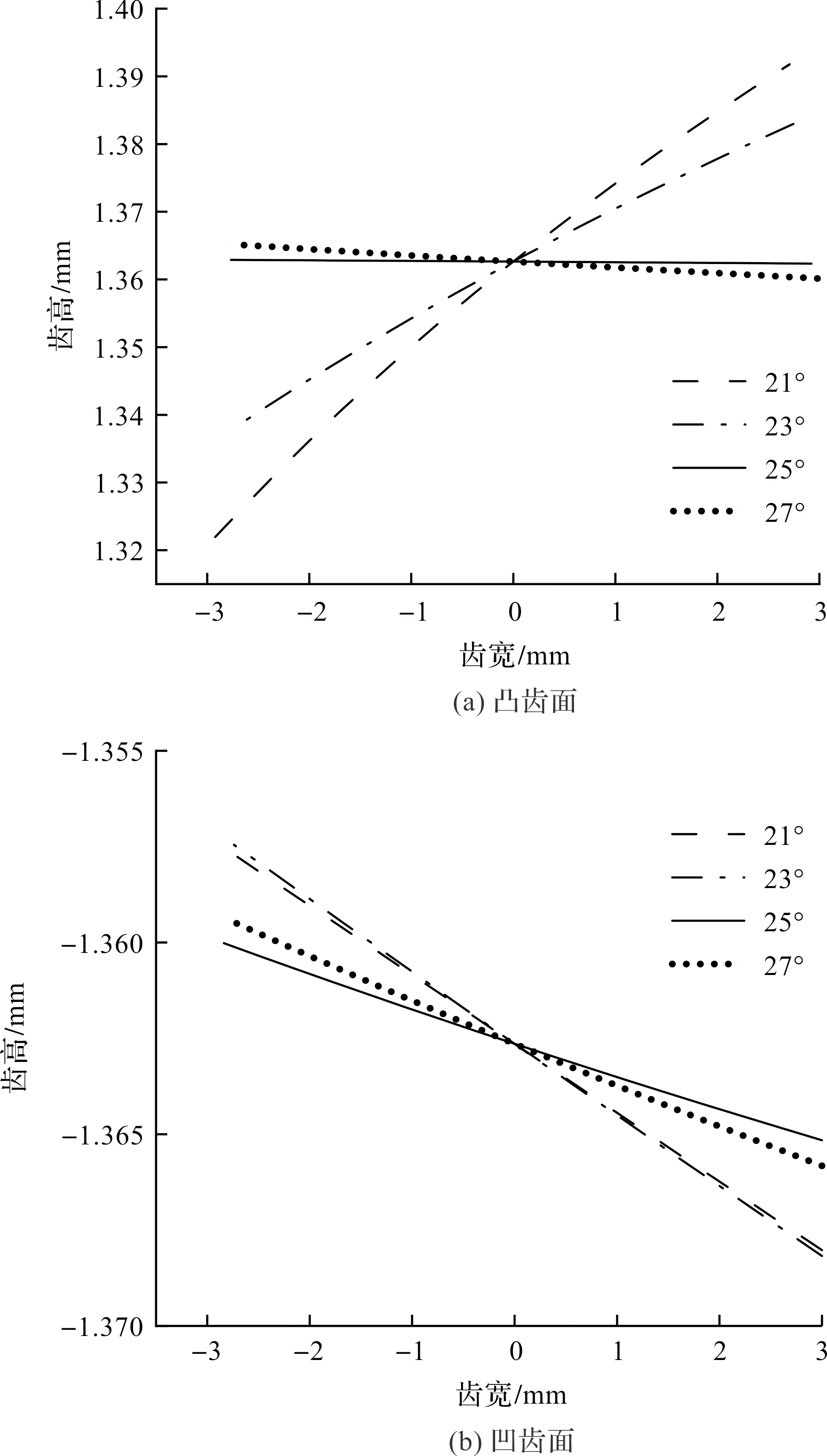
图8 不同螺旋角下的接触迹线

由图8可以看到:当螺旋角低于设计值25.0°时,接触迹线两端的齿高偏移量明显增大,即接触迹线出现不同程度的倾斜,使得接触区呈现一定的对角接触,影响了齿轮的啮合性能,且凸齿面接触迹线受螺旋角变化的影响更大。因此,在设计时应尽量避免该情况的发生。

外凸内凹啮合齿面接触点主曲率如图9所示。

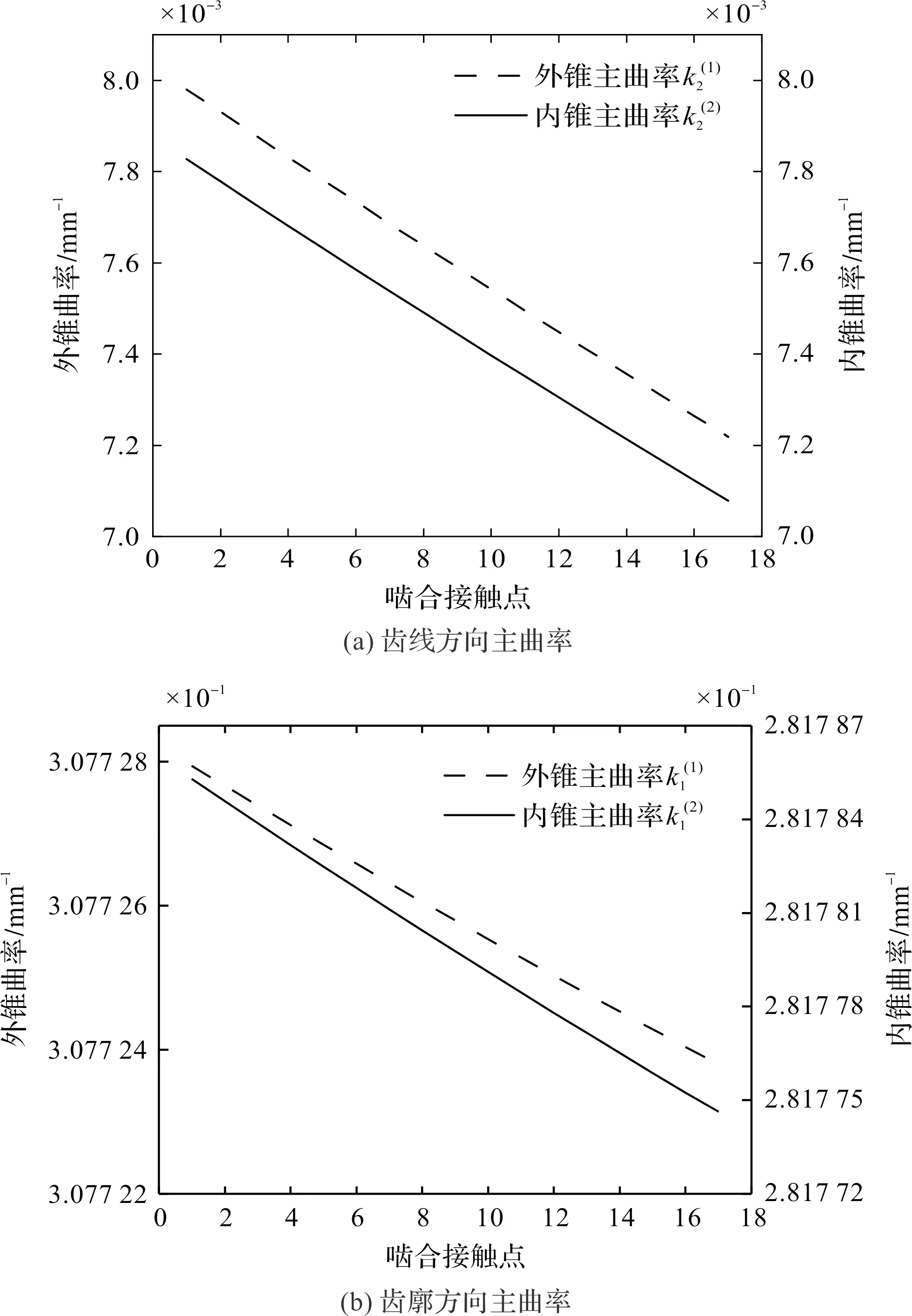
图9 外凸内凹啮合齿面接触点主曲率

外凹内凸啮合齿面接触点主曲率如图10所示。

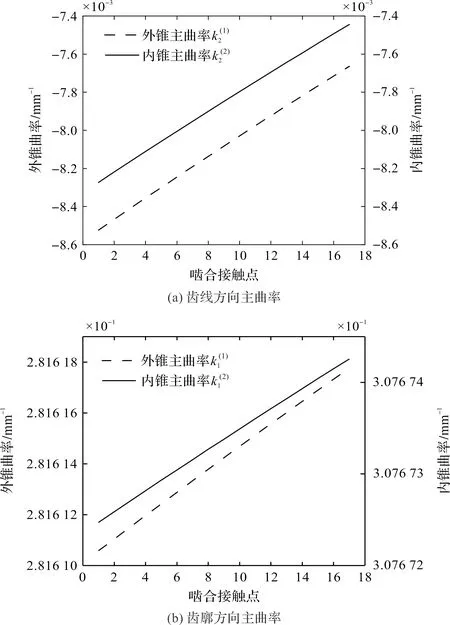
图10 外凹内凸啮合齿面接触点主曲率

在数值上,齿线方向对应的主曲率是所有法曲率中的极小值,齿廓方向主曲率为极大值。

椭圆抛物面如图11所示。

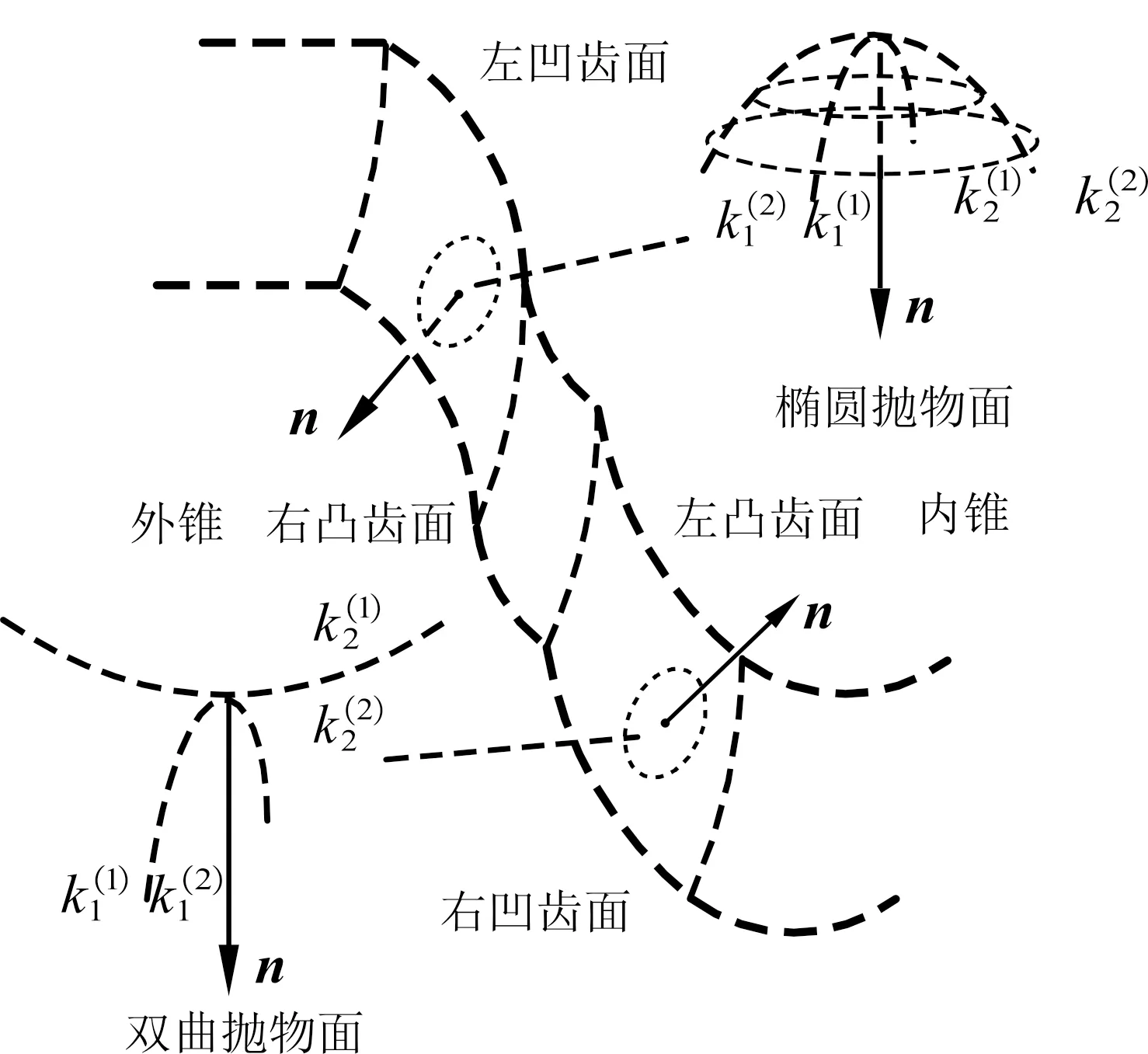
图11 啮合齿面曲面类型

图10中,齿线方向主曲率计算值为负值,齿廓方向主曲率为正值,而此处的啮合齿面类型为图11所示的双曲抛物面。

在上述接触情形下,椭圆长、短轴方向诱导法曲率如图12所示。

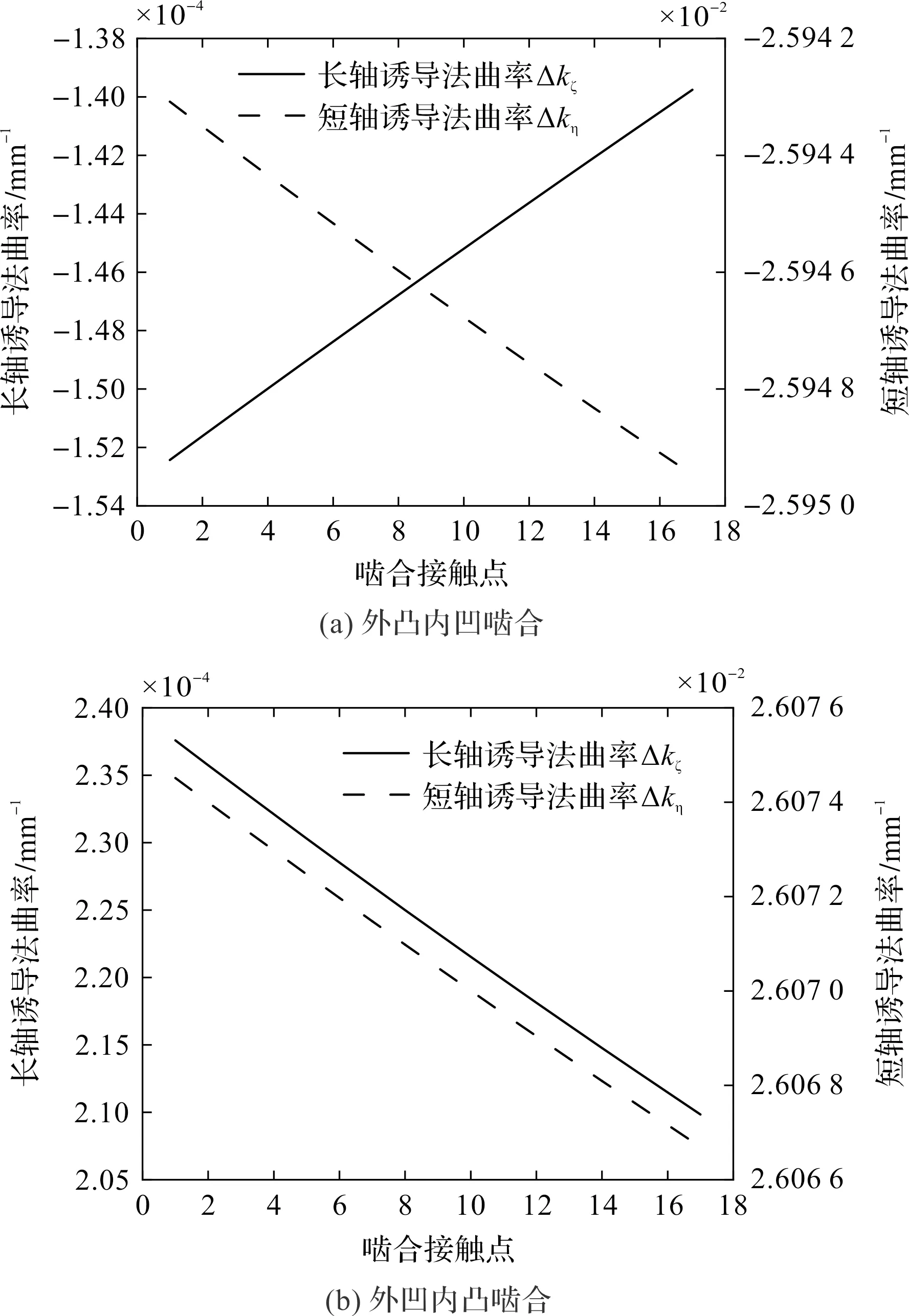
图12 长、短轴诱导法曲率

从图12(a)可知:整个啮合过程中,长、短轴诱导法曲率皆为负值,即在啮合点的任意方向上,都存在对应的内锥凹面法曲率小于外锥凸面法曲率。根据文献[16]所述的检验方法,不难判断出啮合齿面在所有接触点处都不会出现曲率干涉现象;

图12(b)中,长、短轴方向的诱导法曲率均为正值,这是因为外凹内凸啮合齿面与外凸内凹啮合齿面相反,其公法矢量n方向是由实体指向空域。文献[17]指出,此时齿面不发生曲率干涉的条件为任意方向的诱导法曲率都是正值,即它的两个最值也是正值,与笔者的计算结果相符,说明外凹内凸齿面啮合亦不出现曲率干涉现象。

另一方面,诱导法曲率常被用来表征齿面的接触强度,其绝对值越小,说明齿轮传动副的抗弯曲能力越强、抗点蚀强度越高。图12中,长轴方向诱导法曲率基本接近于0,短轴方向诱导法曲率也处于较低水平,且整体变化连续、平缓,证明章动式双圆弧螺旋锥齿轮具有高承载和传动平稳的优点。

4.2 齿轮运动特性分析

在不失一般性的前提下,为了研究啮合齿面间卷吸速度和相对滑动速度的变化规律,笔者给定外锥齿轮输入转速为1 024 r/min,得到外凸内凹啮合齿面运动状态,如图13所示。

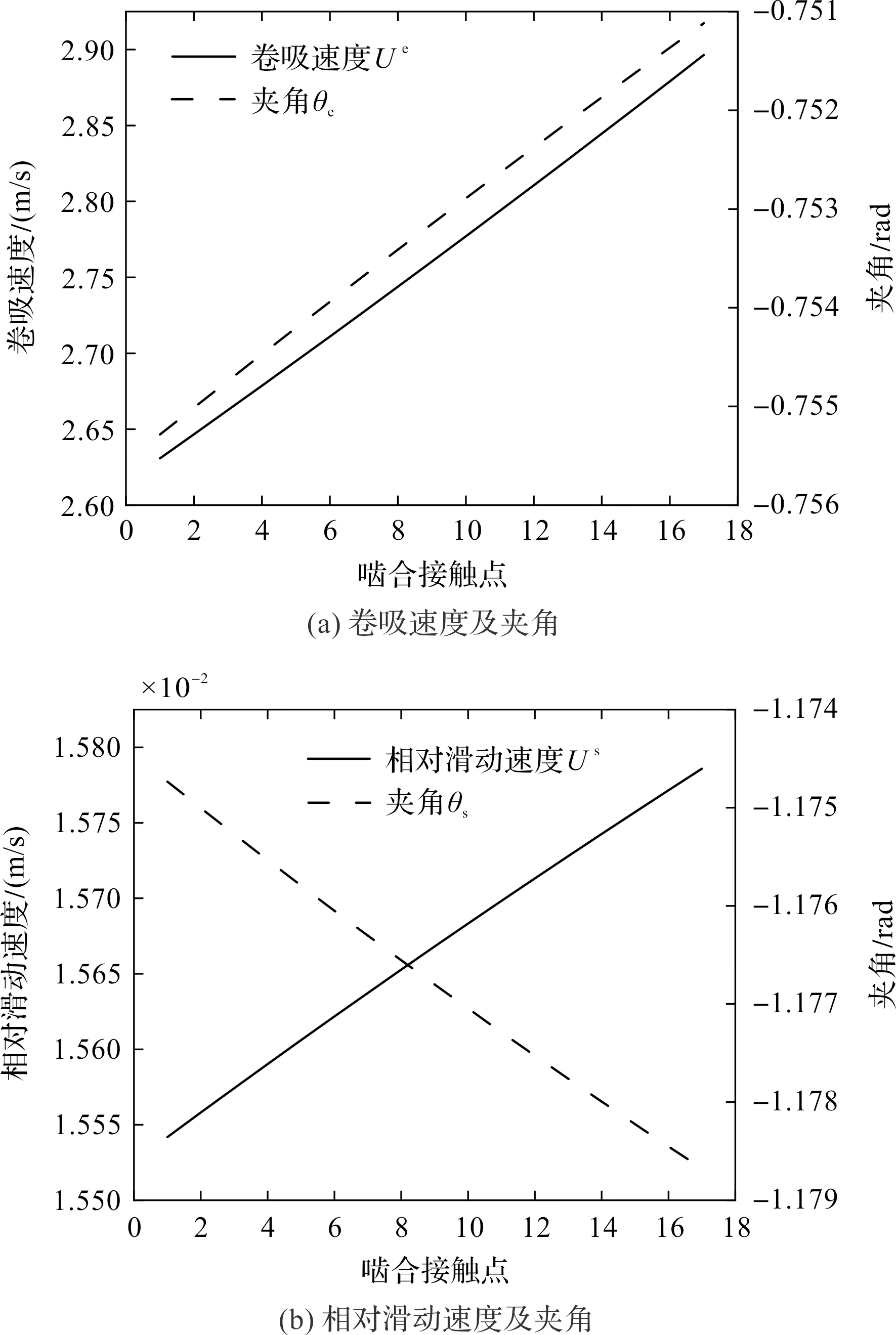
图13 外凸内凹啮合齿面运动状态

外凹内凸啮合齿面运动状态如图14所示。

从齿轮小端到齿轮大端,啮合点的卷吸速度值较大而相对滑动速度值很小,两者的变化幅度不明显,这有利于形成流体动压润滑,并减小磨损。

另外,卷吸速度矢量与椭圆长轴正向之间存在一定的夹角,相对滑动速度矢量则与椭圆短轴方向接近。文献[18]表明,随着卷吸速度与椭圆长轴夹角的增大,中心油膜厚度和最小油膜厚度都将增大。因此,外凸内凹啮合齿面的润滑性能要优于外凹内凸啮合齿面。

齿轮副在接触点处的运动特性如图15所示。

无论是外凸内凹啮合还是外凹内凸啮合,整个传动过程中,齿面滑滚比的值趋于0,且变化缓慢,这表明章动式双圆弧螺旋锥齿轮在工作时接近于纯滚动运动,即由相对滑动引起的齿面磨损很小,且相对均匀;

另一方面,随着螺旋角的增大,外凹内凸啮合的齿面滑滚比逐渐减小,而外凸内凹啮合的齿面滑滚比在设计值25.0°时最小。在相同螺旋角下,外凸内凹啮合的齿面滑滚比始终要小于外凹内凸啮合,表明外凹内凸啮合齿面的传动质量更好。

4.3 齿面接触区域确定

均布载荷作用下得到的齿面接触区域如图16所示。

图16中,各点所受载荷w皆为2 000 N,当量弹性模量E取2.1×1011Pa。

由图16可知:线框所围成的长条矩形区域即为双圆弧螺旋锥齿轮章动传动齿面接触区,由一系列以理论接触点为中心的瞬时接触椭圆共同形成,同齿面各处椭圆长、短轴在大小和方向基本保持一致;其中,凸、凹齿面接触椭圆的长轴大小分别为8.4 mm和7.2 mm,偏离齿宽方向约-1.08°和2.32°;短轴大小分别为0.72 mm和0.79 mm,偏离齿高方向约10.06°和12.26°。

因此,矩形接触区长度取决于齿宽尺寸,宽度则主要取决于椭圆短轴的大小[19]。

负载扭矩M=50 N·m工况下,齿面接触应力的有限元结果如图17所示。

图17 外锥轮齿有限元接触应力分布

图17表明:在一个啮合周期内,单侧轮齿齿面将经历从单点接触到双点接触的相互转换,从而形成两处接触区域;

接触椭圆均沿着齿宽方向由一端向另一端移动,尽管椭圆接触区域的大小随着载荷变化而改变,但方向始终近似平行于齿宽,且仍位于凸、凹齿面的中部,这与数值计算结果十分吻合。

5 结束语

笔者认为明晰齿轮副啮合过程中的曲率变化和运动情况是进行齿轮弹流润滑分析和齿面磨损研究的前提。因此,鉴于有限元法的局限性,笔者采用理论模型分别对章动式双圆弧锥齿轮两工作齿面开展了曲率和运动特性研究,得到的结论如下:

1)诱导法曲率在椭圆长轴方向接近于0,在椭圆短轴方向较小,表明齿轮副具有较高的承载能力和接触强度;两啮合区域皆不产生曲率干涉现象;

2)各接触位置的卷吸速度远大于相对滑动速度,有利于形成油膜;两啮合区域的滑滚比趋近0,表明齿轮的传动过程近似为纯滚动状态,磨损较小;外凸内凹啮合的润滑性能和总体传动质量要优于外凹内凸啮合;

3)齿面接触点分布在凸、凹齿面中部,并沿齿宽方向移动,接触椭圆始终近似平行于齿宽,有限元结果与理论计算一致;

4)螺旋角对齿面接触点的分布以及齿面滑滚比存在一定的影响,故在选取螺旋角时,其值应不低于25.0°。

今后,笔者将进一步考虑包含安装误差在内的理论接触模型,探讨更多参数对齿面接触结果的影响。