水下储气装置的水动力学特性分析*
刘超群,谢迎春,李相坤,白 亮
(中国海洋大学 工程学院,山东 青岛 266100)
0 引 言
截至2022年6月底,我国火电发电量占总发电量的68.24%。作为主要的发电方式之一,火力发电引发了大量的碳排放。大量的碳排放造成了全球变暖和气候变化等危害[1,2]。在此背景下,开发新能源发电成为必然趋势。然而,可再生能源存在着明显的间歇性、随机性等问题,因此,需要储能系统来解决这一问题[3]。
因其调节速率快、容量配置灵活等特点,储能系统受到了业界人士广泛的关注[4]。作为储能技术的一种,水下压缩空气储能十分适用于海上大规模新能源发电系统[5-7]。水下储气装置作为水下压缩空气储能系统中的关键部件,一方面要承受巨大的空气压力,另一方面还要承受复杂多变的环境载荷,这就要求水下储气装置拥有更高的结构强度。
水下储气装置一旦发生损坏,整个储能系统及周围设施与环境将会遭受严重损害[8,9]。因此,笔者选取水下储气装置作为研究对象,对水下储气装置在海流环境下的水动力特性进行研究,为水下储气装置的结构强度设计与水动力学分析提供参考。
对于水下储气装置的流体动力学研究,国内外学者大多采用数值模拟的方法。
孙川等人[10]采用计算流体动力学(computational fluid dynamics,CFD)方法,分析了负压吸附装置的流场特性;但其未对负压吸附装置进行受力分析。王金舜等人[11]采用了大涡模拟方法,对不同海流条件下的水下储气装置流体动力学特性进行了数值模拟;但其未通过实验对数值模拟结果进行验证。WANG Z W等人[12]采用大涡模拟方法,分析了全尺寸水下储能装置时均和瞬态流动结构及其受力特性。VASEL-BE-HAGH A R等人[13-15]分别采用k-ω和LES Dyna-SM两种湍流模型,对气球状储气装置周围的流场结构及受力特性进行了分析,结果发现,储气装置后部可能产生旋涡形式与旋涡脱落过程,并得到了储气装置升阻力系数与涡脱频率;但该研究集中于数值模拟,没有对数值模拟结果进行对比验证。WANG Z W等人[16,17]使用标准的k-ω模型,研究了不同雷诺数条件下气球状储气装置的受力特性及流场结构,结果发现了k-ω模型能够预测时均水动力特性;但k-ω模型不能捕捉到瞬态的湍流特性,且其对于力系数的计算结果偏大。
综上所述,国内外许多学者对水下储气装置进行了流体动力学研究,但大多数研究是采用数值模拟的方法进行的,而很少有研究者采用数值模拟与模型实验相结合的方法。
笔者将已有的气球状储气装置作为研究对象,采用结合数值模拟与模型实验的方法,对气球状储气装置的受力特性及流场结构进行分析,探究气球状水下储气装置的水动力学特性。
1 理论分析
1.1 物理参数定义
为了描述水动力系数的变化规律,笔者引进了无量纲雷诺数Re,其计算公式如下:
(1)
其中:
(2)
式中:ρ为海水密度,kg/m3;U为自由流速,m/s;μ为海水的动力黏度,Pa·s;D为特征长度,m;V为钝体体积,m3。
笔者选择黄海海域作为研究环境。经过调研得知,海水密度为1.025×103kg/m3,平均流速范围为0.1 m/s~0.25 m/s,该海域的平均温度为16.5 ℃,该温度下海水的动态黏度为1.001 4×10-3Pa·s[18]。
根据莫里森方程,升力系数(CL)与阻力系数(CD)由下式进行推导,即:
(3)
(4)
式中:FL,FD为储气装置所受的升力、阻力,N;SL,SD为储气装置在升力、阻力方向上的投影面积,m3。
1.2 LES湍流模型
笔者在对圆柱钝体绕流进行数值模拟时发现,相比雷诺时均法模型,利用LES湍流模型仿真得到的结果更加稳定和精确。并且,自由端效应能够更加容易地被观测到。
笔者将进行过良好检测的Smagorinsky-Lilly LES模型应用于不可压缩流动的Navier-Stokes方程。
经过滤波处理后的方程如下:
(5)
(6)
式中:u为速度,m/s;p为压力,N;ρ为密度,kg/m3;τij为Smagorinsky-Lilly模型中的次网格尺度应力,N。
次网格尺度应力计算公式如下:
(7)
(8)
(9)
(10)
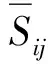
2 水下储气装置水动力实验
2.1 实验模型设计
笔者选取SUBSALVE USA CORPORATION公司生产的专业(PF)系列水下升力气球作为研究对象[19]。
根据水动力实验室的实验条件以及模型材料强度,笔者按照相似准则对模型进行缩放,选定缩尺比为1∶10,从而得到了该次实验的实验模型。
实验模型设计图如图1所示。
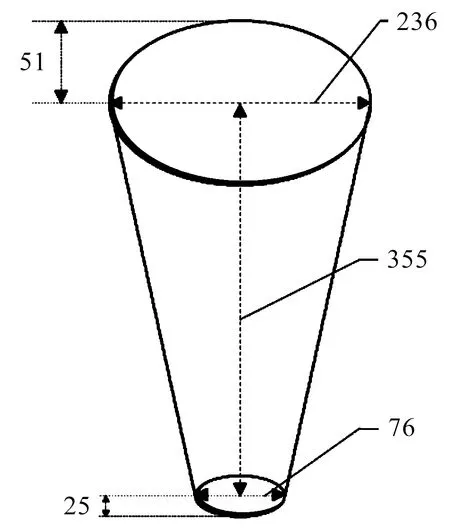
图1 实验模型设计图
在实验模型时,笔者首先利用连接杆将模型与六维力传感器连接起来,然后使用G型夹,将六维力传感器固定在水槽测试段的工装架上。
储气装置实验模型图如图2所示。

图2 储气装置实验模型图
2.2 实验测试平台及实验参数
实验在中国海洋大学海洋工程重点实验室的随机波流耦合水槽中进行。该水槽长60 m,宽3 m,深1.5 m,水槽一侧配有造流系统自动控制软件。
实验过程中,笔者设置水深为1.12 m,实验模型放置于水槽中部,从而保证了稳定流速所需的距离。
实验水槽图如图3所示。

图3 实验水槽图
为保证实验模型与实际模型的雷诺数相似,实验工况的流速计算公式如下:
(11)
(12)
式中:D为储气装置特征直径,m;Dm为储气装置模型特征直径,m;ρ为海水密度,kg/m3;μ为海水的动力黏度,Pa·s;V为海流速度,m/s。
具体实验参数表如表1所示。

表1 实验参数
为保证实验数据的准确性,笔者搭建了包括六维力传感器、振动加速度传感器及流速传感器在内的多传感器融合采集系统。
储气装置模型实验的测试系统如图4所示。
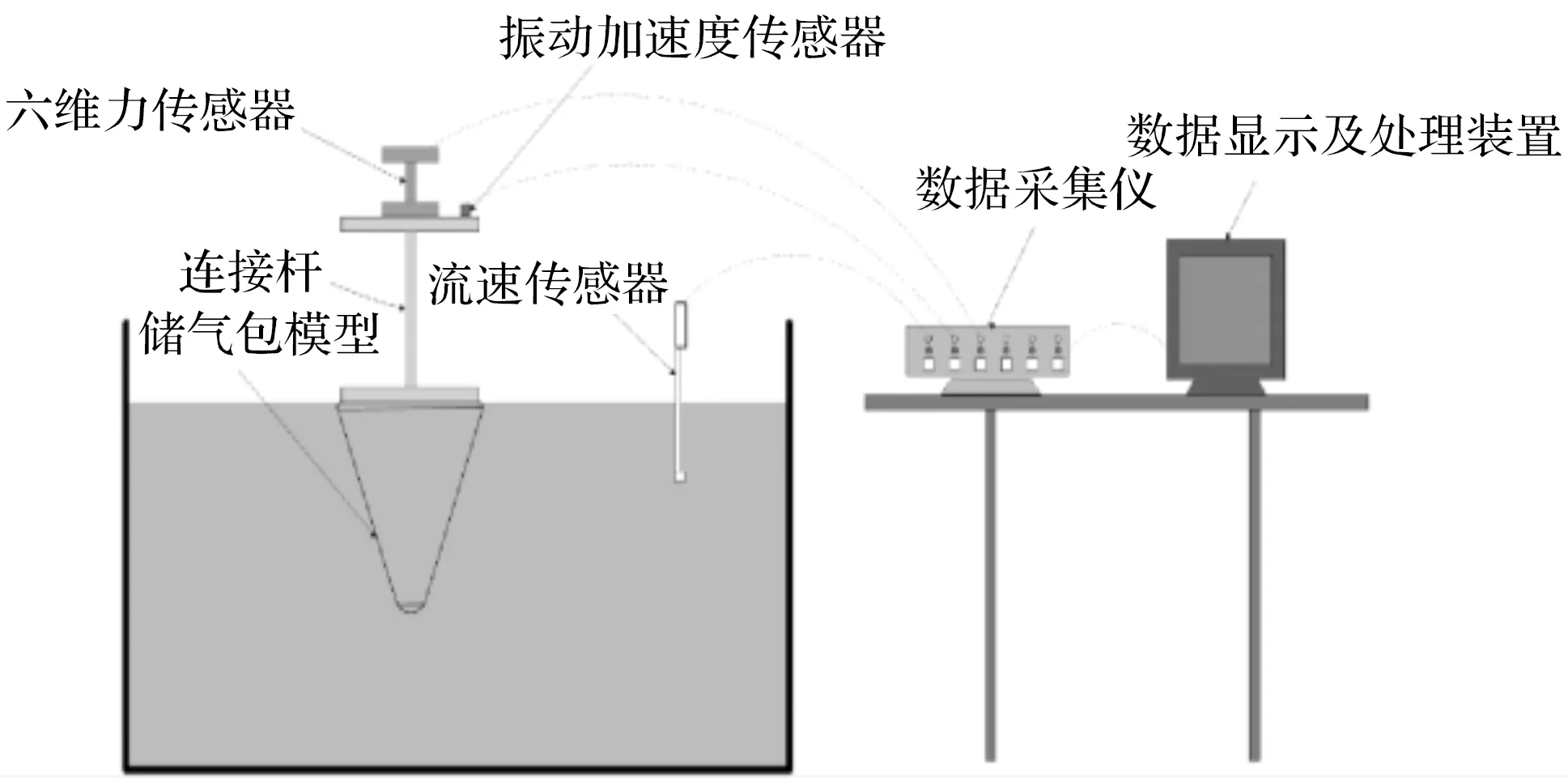
图4 储气装置模型实验测试系统
实验测试系统中,六维力传感器的最大阻力测量量程为±500 N,灵敏度为1 mV/V。所有数据由八通道的无线动态应变采集仪(DH5902)集中采集处理,采集仪的采集频率为10 kHz。流速传感器用于采集实验过程中的实时流速信号。振动加速度传感器用于实时监测模型的振动加速度信号。
为了避免实验数据的偶然性,笔者每组实验重复测试,并取平均值作为实验值。
2.3 实验数据处理
不同流速下,水下储气装置力系数结果图如图5所示。

图5 不同流速下水下储气装置力系数结果图
由图5得:储气装置发生涡脱落时,阻力系数与升力系数会在一定的稳定值范围内波动。随着工况流速的增大,储气装置脉动频率也随之增大。
不同流速力系数平均值如表2所示。

表2 不同流速力系数平均值
由表2可得:随着流速的增大,储气装置承受的阻力和升力逐渐增大。由于涡街的存在,储气装置在横流方向上承受的流体力随时间周期性地变化。当流速为0.4 m/s时,储气装置升力系数的波动表明其侧向存在一对交替产生的旋涡。
3 数值模拟
3.1 数值模型建立
为减少数值模拟的计算量,笔者忽略掉了储气装置的设计细节,将储气装置简化为气球状物理模型,创建了与实验模型尺寸相同的三维数值模型。
简化后储气装置三维模型图如图6所示。

图6 简化后储气装置三维模型图
在进行网格划分时,为保证计算精度,笔者将计算域划分为18块,并在包含储气装置模型的区域中采用非结构化网格,其余区域均采用结构化网格。
同时,为了对储气装置的受力状况进行准确监测,笔者对储气装置壁面进行了边界层网格划分,随后进行网格独立性检验。
网格无关性结果如图7所示。
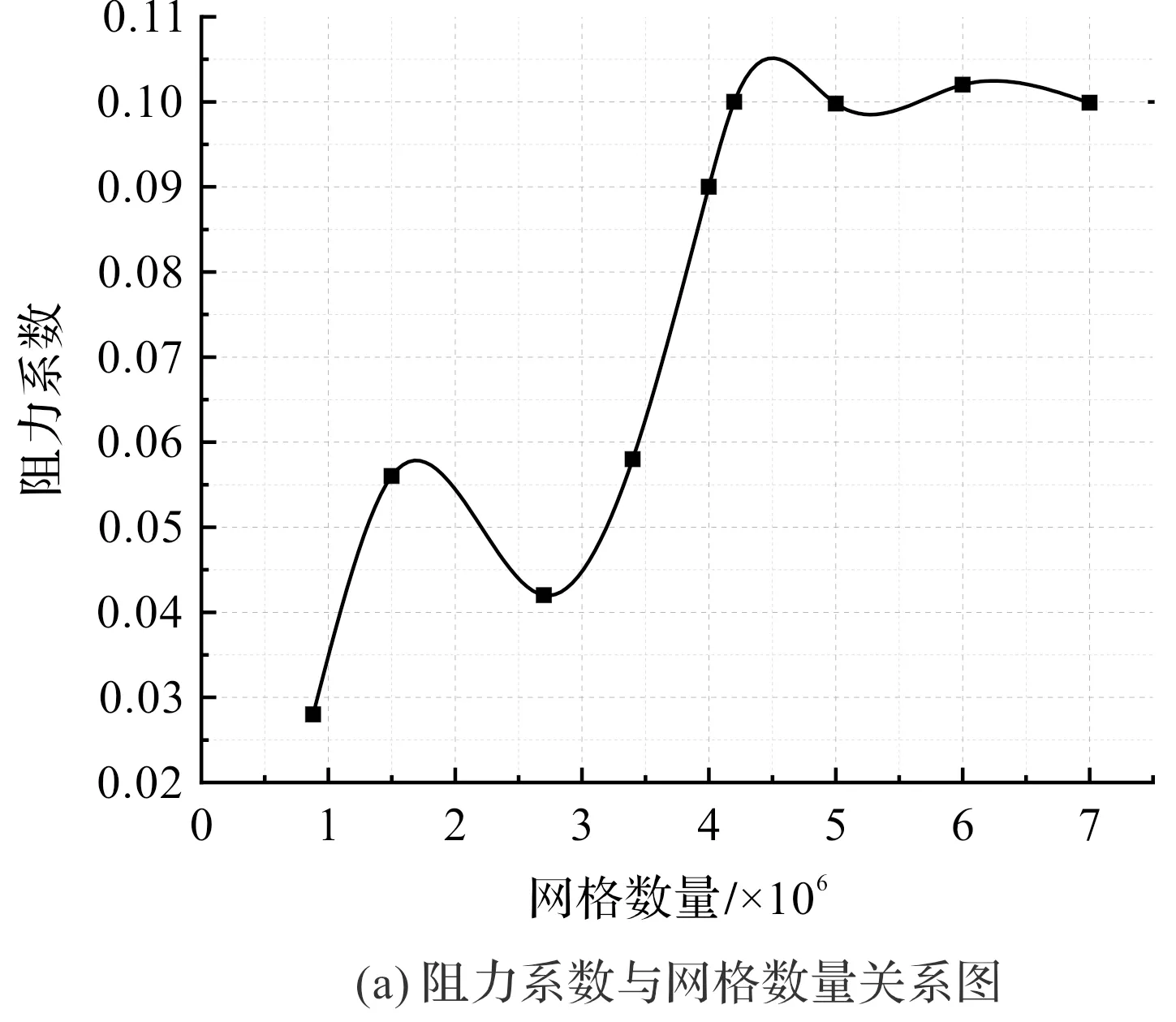
图7 网格无关性结果
由图7可得:在网格数量达到4.1×106个时,储气装置的力系数几乎不再随网格数量变化而变化。
在数值计算过程中,离散格式对求解结果有着重要影响。BREUER W等人[20,21]对此进行了研究,发现了低阶迎风格式无法用于准确捕捉回流区长度。因此,笔者在对储气装置进行数值模拟时,选取高阶迎风格式进行了计算。在进行求解设置时,笔者选用Smag-orinsky-Lilly模型,对亚格子湍流黏度系数进行了求解(Smagorinsky参数设置为0.1)。
为避免在计算过程中因浮点溢出而导致计算中断,笔者在进行数值模拟时对时间步长进行设定。时间步长计算公式如下:
(13)
式中:Δt为时间步长;Vd为X、Y、Z这3个方向上的对应速度,m/s;Δd为3个方向上的对应网格最小尺寸。
3.2 模拟结果分析
3.2.1 流体力分析
笔者将0.4 m/s流速下储气装置的数值模拟结果与实验结果进行比较,得到储气装置力系数时间历程图,如图8所示。

图8 储气装置力系数时间历程图
由图8可得:采用LES湍流模型进行计算时,仿真所得的瞬态结果收敛,且呈现出宽带湍流特征,模型阻力系数和升力系数均趋于平稳;
同时,实验结果略大于仿真结果,其主要原因是实验模型表面存在一定粗糙度,但在数值模拟中模型表面被处理为光滑表面。表面粗糙度增加了实验模型的摩擦阻力,从而导致实验测得的结果较大。
0.4 m/s流速下,实验与仿真力系数平均值如表3所示。

表3 实验与仿真力系数平均值
由表3可得:模型平均升力系数不为零,这是由模型非对称结构导致的。模型下表面的压力大于上表面的压力,因此产生向上的升力。由于模型迎风面的压力比背风面的压力大,因此会产生向后的压阻。
由于实验与仿真所得的模型力系数非常接近,因此,笔者采用LES湍流模型进行数值模拟时,其计算结果是可以接受的[22]。
3.2.2 尾迹流场分析
在流体力学中,涡量是描述旋涡运动的常用物理量[23]。在涡量的计算中,来自流体形变而导致的旋度变化通常会被计算在内,但实际上流体并未发生旋转运动。
所以HUNT J等人[24]提出了Q-criterion,其定义如下:
(14)
式中:Ω为涡量张量;S为变形张量。
根据Q-criterion准则,气球状水下储气装置的瞬时流场涡结构图,如图9所示。
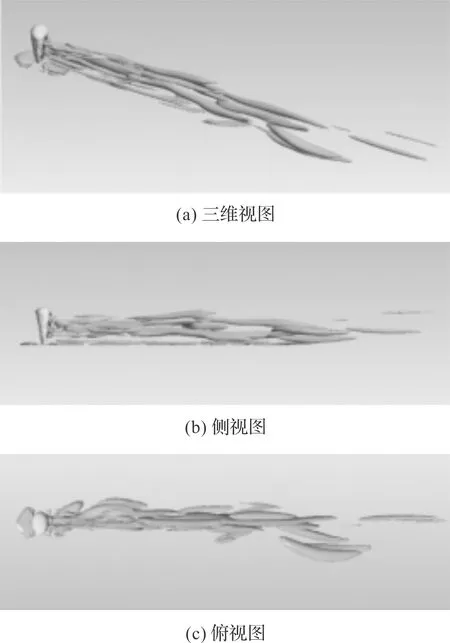
图9 气球状水下储气装置的瞬时流场涡结构
由图9可得:采用LES湍流模型进行数值模拟时,气球状水下储气装置的瞬时流场涡结构和尺度比较复杂,并且流场中存在明显扭曲的卡门涡街;绕流形成的旋涡具有明显的三维结构特征,流经储气装置侧向的流体在装置背风面附近逐渐扭曲形成旋涡结构;背风面附近区域两侧的旋涡关于流场中面对称分布,并经过装置顶部后形成分离涡,从而导致海水向下运动;分离涡在装置半高处附近与侧向向下扭曲的旋涡合流,形成下行海流。下行海流的出现是尾迹流场中竖直方向负速度流体出现的原因之一。
0.4 m/s流速下,流场内的流场流线图如图10所示。

图10 流场流线图
由图10可得:储气装置背风面出现流动分离现象,并伴有旋涡。由于流动的不稳定性,当流体从储气装置流过时,储气装置后部会发生旋涡脱落现象。储气装置表面产生脉动的压力分布,从而使其受到脉动的流体力,导致储气装置出现涡激振动现象。当涡激振动频率与储气装置固有频率接近时,储气装置会发生锁频共振现象,从而受到严重的疲劳损伤。
在0.4 m/s流速下,对称面速度矢量图如图11所示。

图11 对称面速度矢量图
由图11可得:在储气装置工作过程中,由于受到涡流的影响,周围流体的速度响应会增加。但储气装置在水下工作区域的流速非常小,并且储气装置配有压载。所以,储气装置不会对流场产生较大的扰动,也不会对海底环境造成破坏。
4 结束语
笔者采用数值模拟与模型实验相结合的方法,对气球状水下储气装置水动力学特性进行了研究,选择LES湍流模型对气球状水下储气装置进行了仿真分析,并利用实验数据对数值模拟结果进行了验证。
研究结果表明:
1)通过对比实验结果可知,LES湍流模型模拟精度良好,对气球状水下储气装置的流场形态及力系数的仿真结果较为准确;
2)在0.4 m/s流速下,气球状水下储气装置的阻力系数与升力系数分别为0.09和0.04;
3)气球状水下储气装置的顶部结构能够抑制装置顶部附近的回流现象,还可以有效地利用下洗流扰乱侧向旋涡的规则形成与脱落。
笔者当前所得的研究结论对于水下压缩空气储气装置的结构强度设计和水动力学分析具有重要的参考价值和借鉴意义。
未来,笔者将对储气装置充放气过程水动力学特性进行进一步研究。

