基于双频精细复合多尺度排列熵的齿轮箱损伤识别*

刘 心,费 莹,李 倩

(1.桂林电子科技大学 信息科技学院,广西 桂林 541004;2.三门峡社会管理职业学院 机电工程学院,河南 三门峡 472000;3.苏州大学 金螳螂建筑学院,江苏 苏州 215123;4.浙江汽车职业技术学院 电子工程系,浙江 临海 317000)

0 引 言

在长期重载、高速运行时,齿轮易出现断裂和磨损等损伤[1]。齿轮箱出现损伤后,其振动会明显加剧,且呈现出非线性、非平稳的特点[2]。目前,常用的分析方法可以归为以经验模态分解为代表的信号分解方法[3,4]和以信息熵为代表的熵值方法[5]。

目前,以排列熵[6]和多尺度排列熵[7,8](multiscale permutation entropy,MPE)为代表的特征提取方法被广泛应用于齿轮箱的损伤识别。

武哲等人[8]将MPE应用于齿轮箱的损伤识别,结果表明MPE能用于有效地提取齿轮箱的损伤特征;但是MPE的粗粒化处理受数据长度的限制较大,粗粒序列的长度随着尺度的增加而变短,损伤识别结果会产生较大偏差[9]。董治麟等人[10]采用了基于复合多尺度排列熵(composite multiscale permutation entropy,CMPE)的方法,CMPE改进了粗粒化的构造方式,使得粗粒序列包含的信息更完整,诊断结果表明CMPE的性能优于MPE;但是CMPE的复合粗粒化处理遗漏了信号中的特征信息。LI Yong-jian等人[11]提出了基于RCMPE的方法,验证了RCMPE的性能优于CMPE;但是RCMPE的粗粒化处理忽略了信号的高频深层次特征[12]。

针对基于粗粒化的多尺度分析方法无法提取嵌入在信号中的高频信息,导致特征提取不完整这一问题,TIAN Jing等人[13]提出了基于层次排列熵(hierarchical permutation entropy,HPE)的方法,并将其应用于轴承的故障诊断。与MPE不同,HPE采用层次化处理,将时间序列根据层次处理分解为低频和高频分量,分别反映了信号的低频和高频信息;其不仅能进行多尺度分析,而且能提取信号的低频和高频特征,诊断结果也表明,HPE因考虑了信号的低频和高频特征,在性能上要优于MPE;但是HPE直接对原始信号进行分析,未消除信号中噪声的干扰。YANG Cheng等人[14]根据HPE和MPE的优势,提出了基于层次多尺度排列熵(hierarchical multiscale permutation entropy,HMPE)的方法,全面提取了信号特征,得到的轴承损伤识别结果验证了HMPE不仅优于基于粗粒化方法的CMPE,而且优于基于层次分析方法的HPE;但是HMPE仍然无法缓解噪声干扰,其抗噪性较差。

由于故障诊断领域样本较小,且非线性较强,因此常使用支持向量机(support vector machine,SVM)作为模式识别分类器[15]。徐乐等人[16]采用了局部均值分解和能量熵相结合的方法,提取了特征向量,并采用SVM实现了故障的识别目标;但是SVM的参数需人为设置,泛化性较差。夏理健等人[17]采用粒子群优化算法对SVM的参数进行了优化,并将其用于滚动轴承的故障诊断;但是粒子群优化算法(particle swarm optimization,PSO)的全局优化性能较差。葛红平等人[18]采用鲸鱼算法对SVM的参数进行了优化,并将其应用于滚动轴承的损伤识别,结果验证了WOA-SVM的优越性。

针对RCMPE无法提取信号的高频特征,以及HPE的抗噪性较差等缺陷,笔者提出了一种DFRCMPE方法,以全面可靠地提取损伤特征。DFRCMPE采用了WPD与RCMPE相结合的方法,不仅避免了RCMPE方法无法提取时间序列高频信息的缺陷,还减小了原信号中的噪声干扰。此外,鉴于WOA-SVM在模式识别中的优越性,以及DFRCMPE在特征提取中的有效性,笔者提出了基于DFRCMPE和WOA-SVM的齿轮箱损伤识别方法。

首先,笔者采用WPD对振动信号进行两层分解,得到信号的低频和高频小波系数,以突出信号的故障特征,并减小噪声干扰;随后,采用RCMPE提取两组小波系数的熵值,构造损伤特征;最后,将损伤特征输入至WOA-SVM中进行齿轮箱的损伤识别,并以齿轮箱损伤数据为对象,对所提损伤识别方法的有效性和泛化性进行验证和对比。

1 基础理论

1.1 小波包分解

小波包分解(WPD)能够实现信号的全频带、多层次的分割,不仅具有小波变换的良好局部时频分析这一优点,而且能够实现对高频成分的进一步分割。经过WPD后的数据,其高频频带序列被突出,增强了信号分析的分辨率[19]。

WPD的信号分解原理如图1所示。

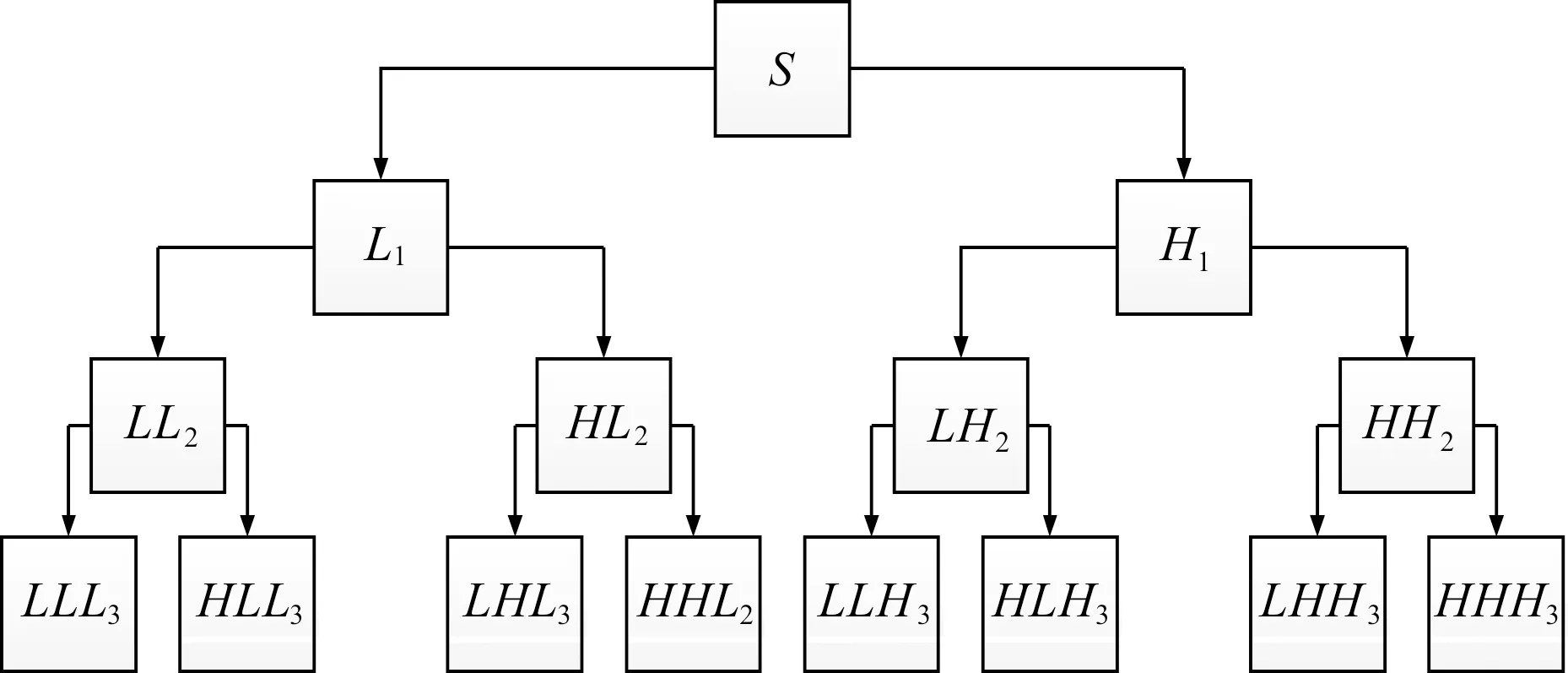
图1 小波包数据分解的示意图

图1中,笔者对原始信号进行WPD后,能够得到低频和高频分量,此时再进行特征提取能够获得更深层次的特征,减少噪声干扰。

WPD的原理如下:

若数据{gn}n∈Z符合:

(1)

则基于小波函数ψ(t)和尺度函数φ(t)能生成一组递归函数ωn∈L2(R),n=1,2,…符合下列关系:

ω0(t)=φ(t),ω1=ψ(t)

(2)

(3)

其中,uk=(-1)kg1-k,表明两个系数存在正交关系。

基于式(3)生成的序列{ωn(t)}n∈Z即基函数ω0(t)=φ(t)的小波包。

笔者继续对小波细节数据进行分解,即获得数据x(t)的WPD和重构表达式。

数据x(t)的WPD表达式如下:

(4)

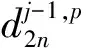
小波包的重构表达式为:

(5)

1.2 精细复合多尺度排列熵

基于精细复合多尺度排列熵(RCMPE)的方法是根据多尺度排列熵的原理对粗粒化方式进行改进后得到的。MPE首先对数据开展不同尺度的粗粒化处理,再计算其排列熵。其优点为计算效率高、原理简单;其缺陷在于对数据开展粗粒化处理时,没有考虑数据点之间的关系,数据长度较短时,所计算的熵值偏差较大,结果不可靠[20]。而RCMPE首先计算每个粗粒序列的排序模式π的概率,再取这些排序模式概率的平均值,最后基于信息熵的定义求解RCMPE;这样能缓解MPE在粗粒化处理时存在的数据遗漏和偏差大等缺陷。

RCMPE的理论如下[21]:

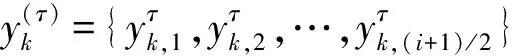
(6)

对于每个排序模式,其相对概率计算如下:

(7)

3)随后重复步骤2),求得所有排序模式的平均概率,则RCMPE定义如下:

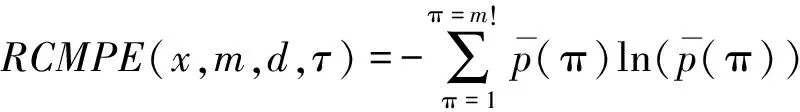
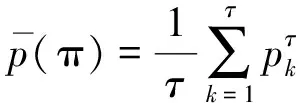
(8)

在RCMPE方法中,需要预先设置嵌入维数m、时间延迟d和尺度因子τ。m过大,则无法检测数据中的动态波动;m过小,则嵌入向量中的状态(符号)数量过少,可能会无法使用RCMPE算法进行计算。

在LI Yong-jian等人[11]的研究中,对RCMPE在滚动轴承损伤识别中的应用进行了研究,推荐设置嵌入维数m为5,时间延迟d=1。尺度因子过小会造成信号特征信息反映不全面,为此笔者设置尺度因子τ=20。

1.3 双频精细复合多尺度排列熵

RCMPE基于粗粒化处理来实现信号的多尺度分析,这会导致其无法提取信号的高频特征。笔者根据层次排列熵的层次化处理这一设想,利用WPD对RCMPE方法进行改进。WPD类似于层次分解,将信号分解为反映数据低频和高频特性的分量。

考虑到WPD能够将信号分解为低频和高频分量的优点,笔者基于RCMPE,提出了双频精细复合多尺度排列熵(DFRCMPE)方法,其原理如下:

1)对于时间序列{x(i),i=1,2,…,N},对其进行WPD,得到时间序列的低频和高频系数:

(9)

2)在相同参数下,利用RCMPE分别计算小波低频系数和高频系数的熵值:

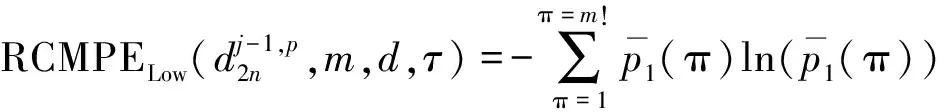
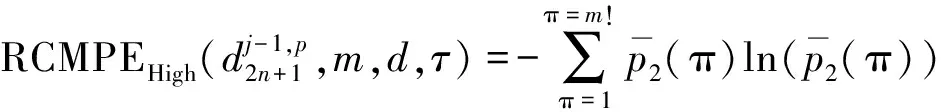
(10)

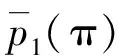
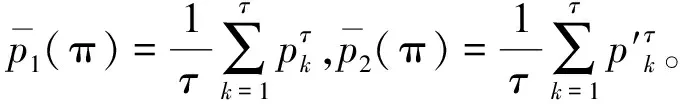
3)因此,可以定义DFRCMPE如下:

DFRCMPE=[RCMPELow;RCMPEHigh]

(11)

1.4 鲸鱼算法优化支持向量机

1.4.1 鲸鱼优化算法

鲸鱼优化算法(WOA)是根据模拟座头鲸的捕猎行为而开发的一种群体智能优化算法,由3个部分组成:包围猎物、泡网攻击和搜寻猎物[22]。

1)包围猎物。座头鲸在猎杀目标时,可以迅速找到目标的空间坐标并进行包围,其数学形式如下:

Xj+1=Xj-A×D

(12)

(13)

式中:j为当前的迭代次数;X*目前取得最佳解的坐标向量;X为鲸鱼的坐标向量;A,C为系数向量。

A,C的数学形式如下:

A=2a×r-a

(14)

C=2r

(15)

式中:a为收敛系数;r为[0,1]内的任意值。

2)泡网攻击。座头鲸猎杀目标时,在缩小气泡网的同时,顺着螺旋式上升的路径朝着最佳解方向移动,其数学形式如下:

(16)

式中:D′为目标猎物与座头鲸之间的距离;b为对数螺旋系数;l为[-1,1]范围内的任意值。

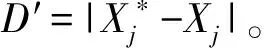
鲸鱼捕猎时,缩紧包围与螺旋位置坐标更新同时进行,其数学模型定义如下:

(17)

式中:p为[0,1]内的随机值。

3)搜寻猎物。座头鲸通过分享彼此之间的相互位置来随机搜寻猎物,其描述如下:

Xj+1=Xrand-A×D

(18)

D=|C×Xrand-Xj|

(19)

式中:Xrand为随机选择的鲸鱼坐标向量。

1.4.2 WOA-SVM流程

SVM是一种典型的监督学习方法,但SVM的优异性能受到核函数C和惩罚系数g的影响。因此,笔者利用WOA算法对SVM的关键参数进行优化,以实现SVM核心参数的自适应选择。

鲸鱼算法优化支持向量机(WOA-SVM)的优化流程图如图2所示。

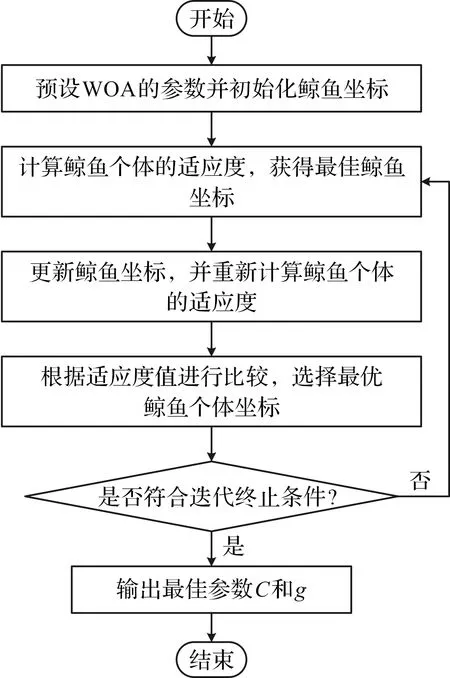
图2 WOA-SVM的流程图

详细流程如下:

1)构建训练样本和测试样本,并归一化;

2)初始化WOA的参数。预先设置WOA的参数和SVM的参数范围设置,选择RBF为核函数,并随机初始化鲸鱼的位置;

3)以训练集的识别准确率为适应度,计算每条鲸鱼的适应度,搜索并保留当前种群中最优鲸鱼个体的坐标;

4)基于WOA对鲸鱼位置进行优化,刷新鲸鱼的个体位置;

5)求出更新后各鲸鱼个体的适应度,更新并保留当前最佳鲸鱼的个体位置;

6)判断是否符合优化终止条件,若符合,结束优化;否则,重复循环;

7)输出最优鲸鱼个体适应度值所对应的坐标向量,即最优惩罚系数C和核参数g。

2 基于DFRCMPE和WOA-SVM的识别方法

为从齿轮箱中提取出全面且高质量的损伤特征,笔者提出了基于DFRCMPE和WOA-SVM的齿轮箱损伤识别方法。

该识别方法流程的具体步骤如下:

1)利用加速度计采集齿轮箱在正常、点蚀、磨损、断齿、点蚀+磨损、断齿+磨损等6种不同损伤状态下的振动信号。每种损伤包含M个样本,随机抽取其中的H个样本用于训练,剩余M-H个样本用于测试;

2)对样本进行两层小波包分析(WPD),得到两个低频小波系数和高频小波系数,随后计算每个小波系数的RCMPE值,得到样本的DFRCMPE值;

3)利用鲸鱼优化算法对SVM进行优化,并将训练样本的损伤特征输入至WOA-SVM中进行训练,构建参数最优的SVM分类模型;

4)将测试样本的损伤特征输入至WOA-SVM分类模型中进行损伤辨识,完成齿轮箱的损伤检测任务。

3 齿轮箱损伤识别实验

3.1 数据的采集和介绍

此处笔者采用某公司的QPZZ-II型旋转机械损伤模拟装置,快速模拟旋转机械的各种损伤状态,并采集其振动信号。

该实验装置如图3所示。

该装置的主要结构包括变速齿轮箱、三相交流电动机(0.75 kW)、联轴器、转轴和旋转圆盘等。其中,齿轮箱中的大齿轮模数为2,齿数为75,小齿轮模数为2,齿数为55,大小齿轮的材料均为S45C。

基于该装置模拟齿轮箱在不同损伤状态下的运转情况,笔者采集其在正常、点蚀、磨损、断齿、点蚀+磨损、断齿+磨损等6种不同损伤状态下的振动信号,设置采样频率为5 120 Hz。

笔者充分考虑齿轮箱的复杂工况环境,模拟了在转速为880 r/min、加载0.1 A电流下的齿轮箱运行;并用传感器采集了53 248个振动数据点,将其分成25组,每组4 096个数据点。

具体采样方式为以一个长度为4 096的滑动窗口,以2 048的重叠长度进行样本的滑动分割。

齿轮箱6种工况的振动信号和频谱如图4所示。

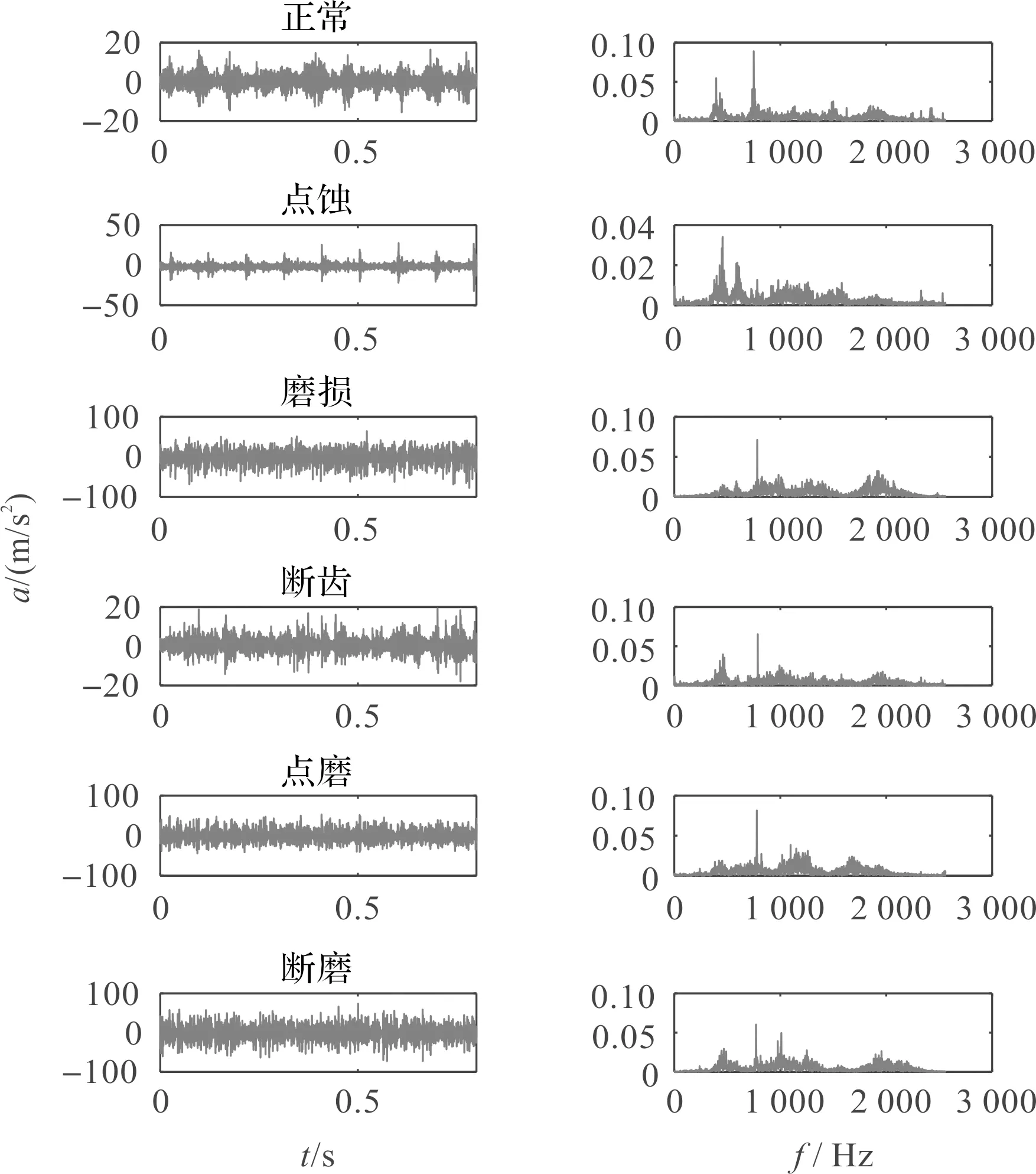
图4 齿轮箱不同损伤状态的振动信号及频谱

图4中,虽然振动信号具有比较明显的冲击特性,但无法准确、智能地判断齿轮箱的损伤类型,需要对其进行进一步处理。

3.2 损伤特征提取和分类识别

首先,对样本进行两层WPD分解。

以正常振动信号为例,其分解后的低频和高频小波系数如图5所示。

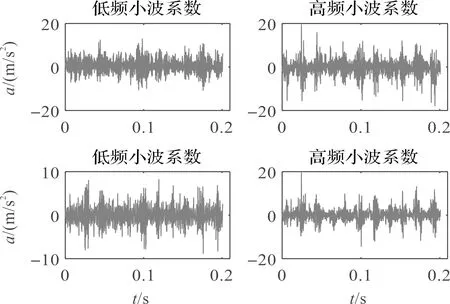
图5 正常振动信号的WPD

随后,计算所有样本的两组低频小波系数和高频小波系数的RCMPE,对样本的DFRCMPE进行分析,结果如图6所示。

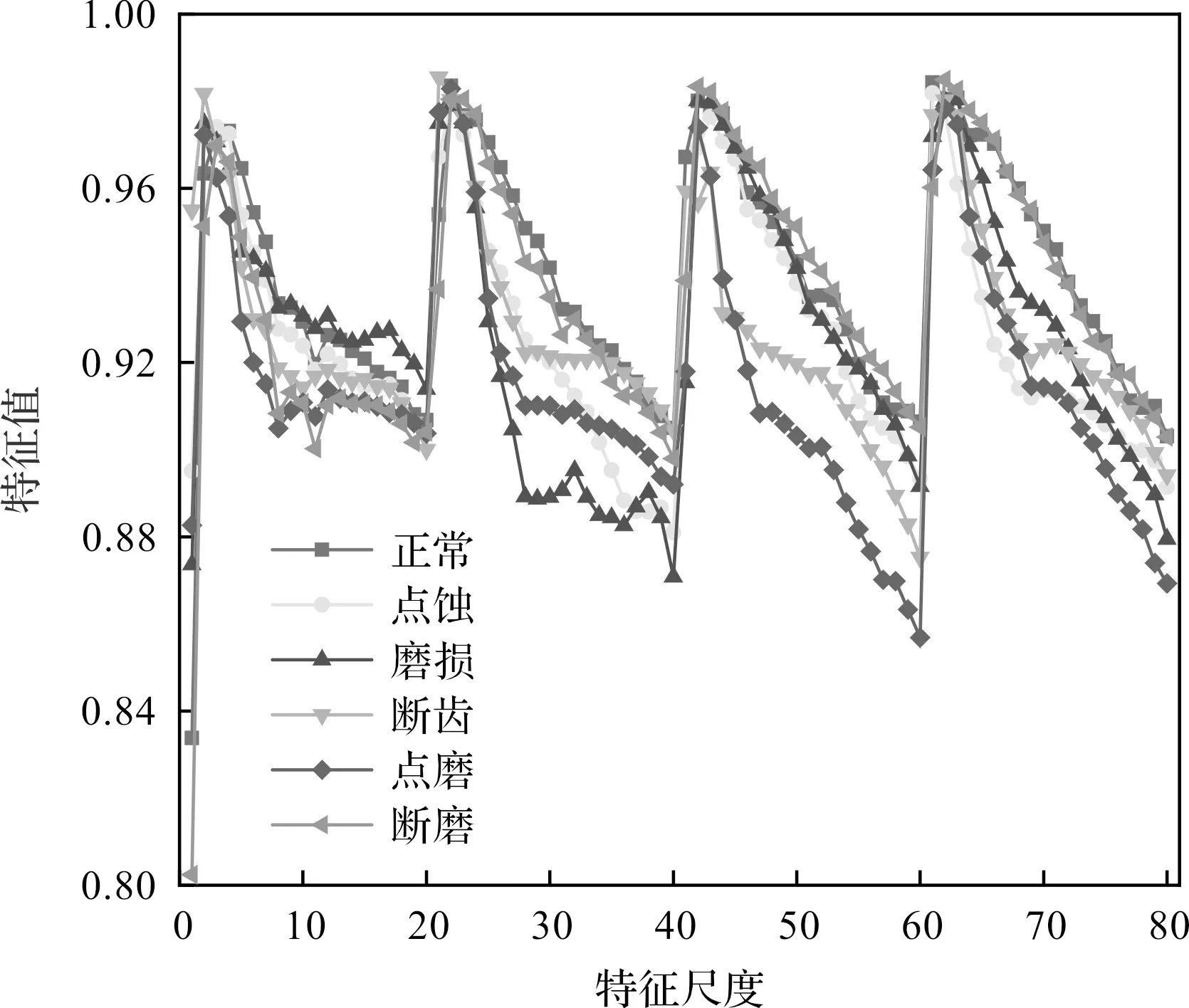
图6 齿轮振动信号的DFRCMPE

由图6可知:DFRCMPE能够估计不同特征尺度的信号复杂度,避免信号中残留噪声对其产生的影响。虽然DFRCMPE在部分工况下的特征值相对接近,但是其能够提取多组特征,采用多个尺度特征相结合的方法对各工况进行辨识,增强了对信号的表征能力。因此,DFRCMPE可以有效提取多尺度损伤特征信息,从而精确反映齿轮箱系统的损伤特性及规律。

笔者将所有样本采用DFRCMPE进行处理后,随机选取各工况60组和90组样本用于训练和测试,以模拟小样本分析的实际需求。笔者将正常、点蚀、磨损、断齿、点磨和断磨的分类标签分别设置为1—6;将特征向量输入到WOA-SVM中进行训练和识别,损伤识别结果如图7所示。

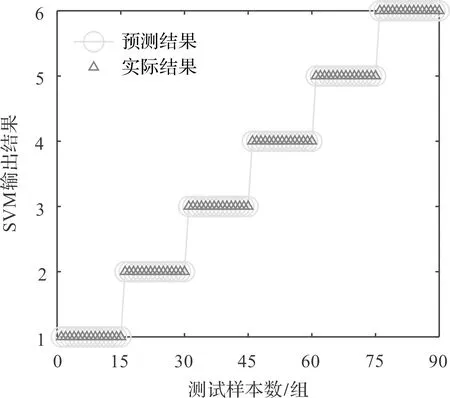
图7 所提损伤识别方法的分类结果

由图7可知:所提损伤识别方法的识别准确率达到了100%,证明其能够用于有效地识别齿轮箱的不同损伤类型。

随后,为了证明所提损伤识别方法的有效性和优越性,笔者将其与基于精细复合多尺度样本熵(RCMSE)[23]、精细复合多尺度模糊熵(RCMFE)[24]、RCMPE[25]、精细复合多尺度散布熵(RCMDE)[26]的损伤特征提取方法进行准确率对比,结果如图8所示。

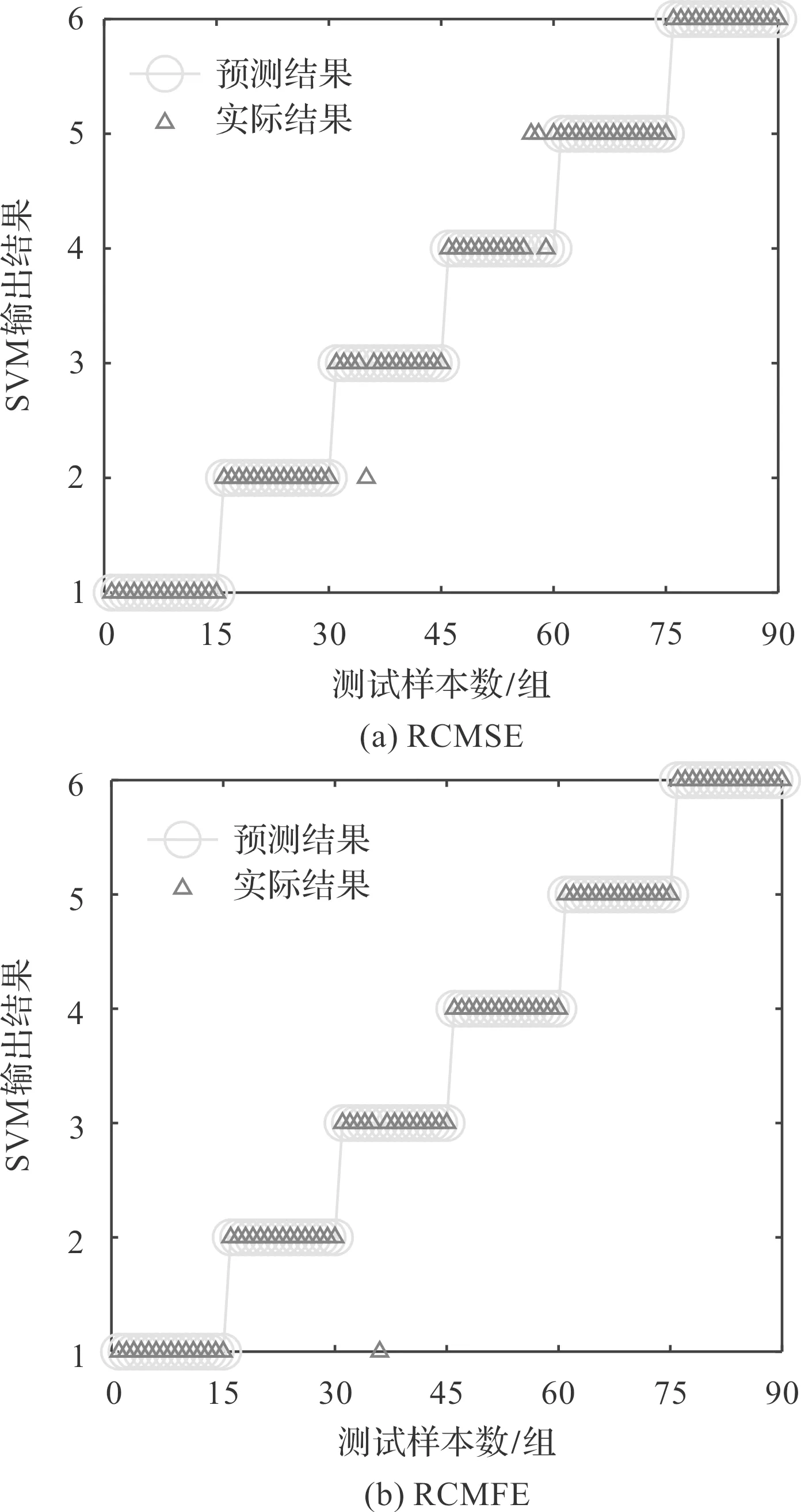
图8 4种特征提取方法的WOA-SVM识别结果

由图8可知:4种特征提取方法的识别结果均出现了错误分类的样本,证明这4种方法无法完全有效地识别齿轮箱的故障。

DFRCMPE方法和图8中4种特征提取方法的详细诊断结果如表1所示。

由表1可知:在5种特征提取方法中,后4种的分类准确率分别为95.56%、98.89%、98.89%和96.67%,均低于第1种DFRCMPE方法,证明了DFRCMPE方法的优越性;同时可知,DFRCMPE方法在各个工况下都具有较高的准确度,说明了该方法具有较好的鲁棒性。

接着,为了评估不同方法在提取故障特征时的效率,笔者统计了5种方法的特征提取时间,结果如表2所示。

表2 5种特征提取指标的效率

由表2可知:DFRCMPE方法的效率最低,需要216.17 s去提取故障特征,但考虑到DFRCMPE方法的准确率达到100%,说明其具有一定的应用潜力。

随后,笔者对DFRCMFE、RCMSE、RCMFE、RCMDE这4种方法进行了稳定性评估,对5种特征提取方法在10次实验下的分类结果进行了统计,详细结果如图9所示。

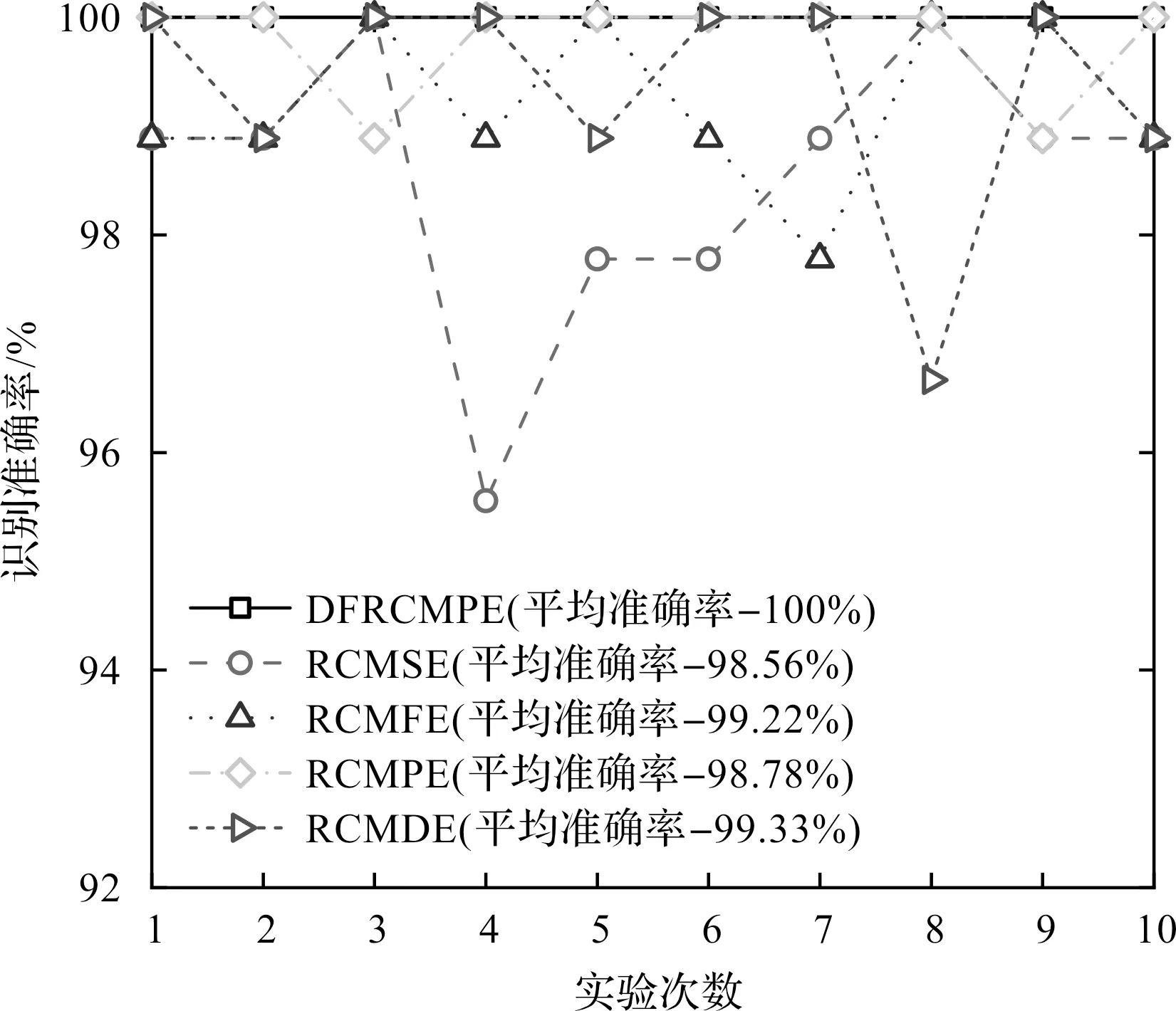
图9 多次实验的分类准确率

由图9可知:DFRCMPE方法在10次分类中都取得了100%的识别准确率,优于另外4种方法,证明了DFRCMPE方法的稳定性和优越性。其他4种方法的分类结果在多次实验中出现了波动,这证明其他方法每次获得的结果不一定可靠。

随后,为了进一步评估DFRCMPE方法在小样本识别中的有效性和可行性,笔者对不同数量训练样本(训练样本的数量分别为5、10、15、20)的分类表现进行了研究,结果如图10所示。

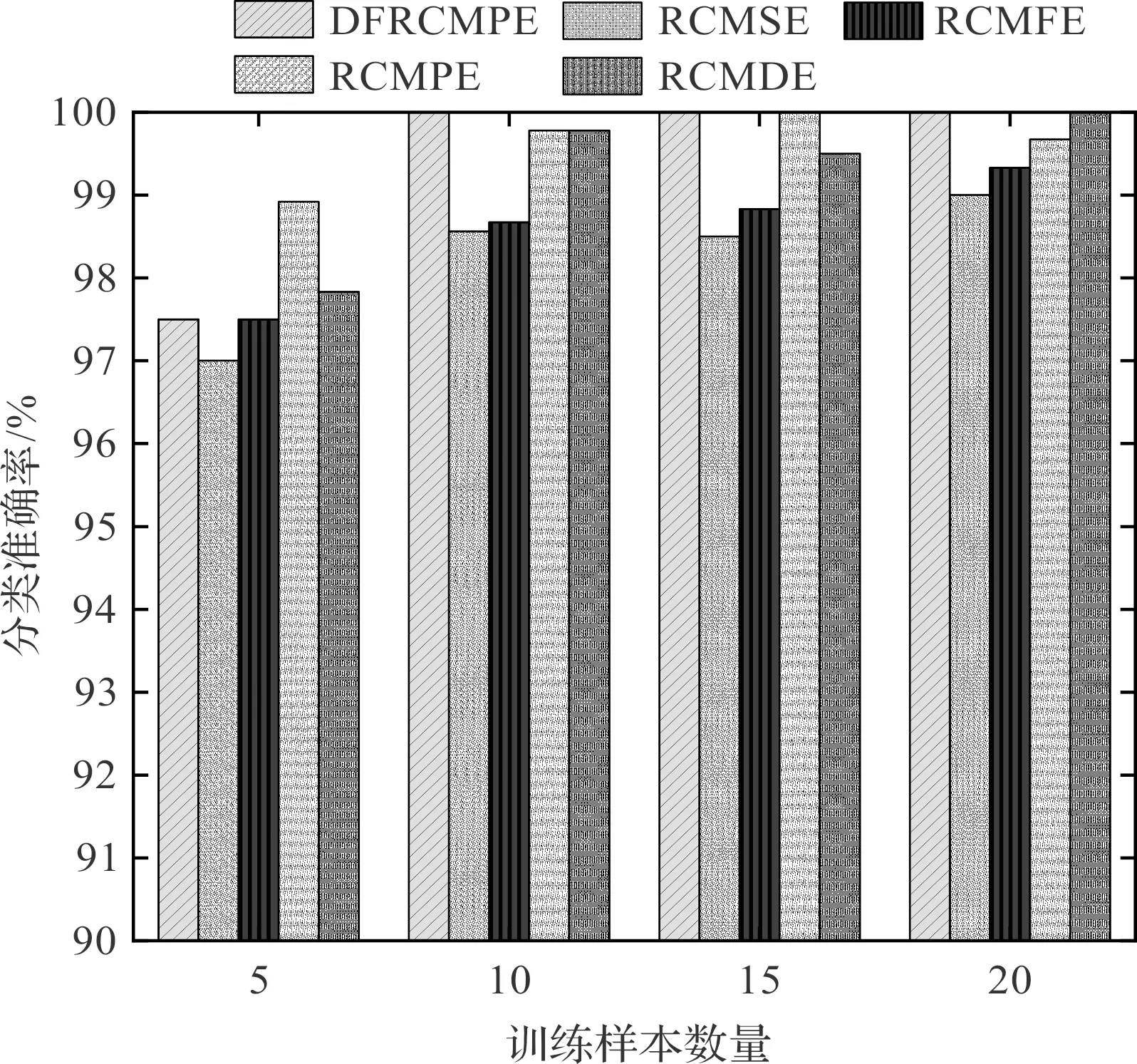
图10 不同训练样本数量的分类准确率

由图10可知:DFRCMPE方法在训练样本为10时,已经取得了100%的准确率,而其他4种方法需要样本的数量更多(例如,RCMPE在训练样本数量为15时,达到了100%的准确率;RCMDE在训练样本数量为20时,达到了100%的准确率,等等)。这说明其他方法需要较多的训练样本才能达到最佳效果,而DFRCMPE方法适用于小样本的损伤识别。

为了验证WOA-SVM分类器的优越性,笔者将优化算法替换为遗传算法(genetic algorithm,GA)、粒子群优化算法(PSO)、人工鱼群算法(artificial fish school algorithm,AFSA),将这5种方法提取的特征输入至GA-SVM、PSO-SVM、AFSA-SVM和SVM分类器中,进行模式的识别。

优化后的SVM参数如表3所示。

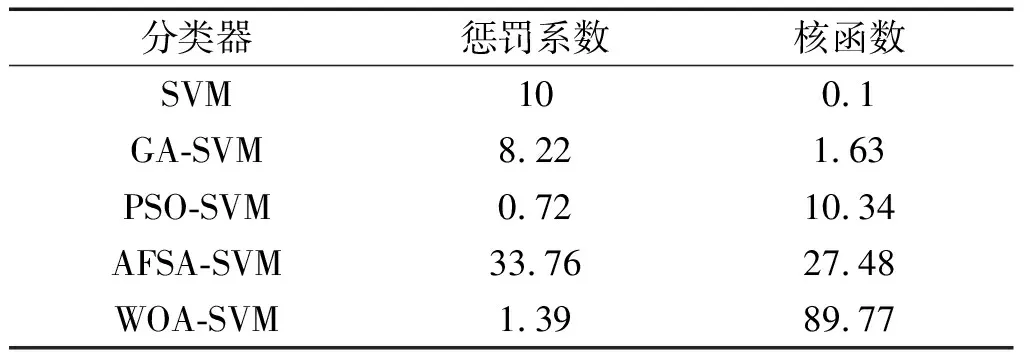
表3 不同SVM分类器的参数设置

笔者利用优化后的参数构建SVM分类器,将故障特征输入至优化后的分类器进行故障识别,结果如图11所示。

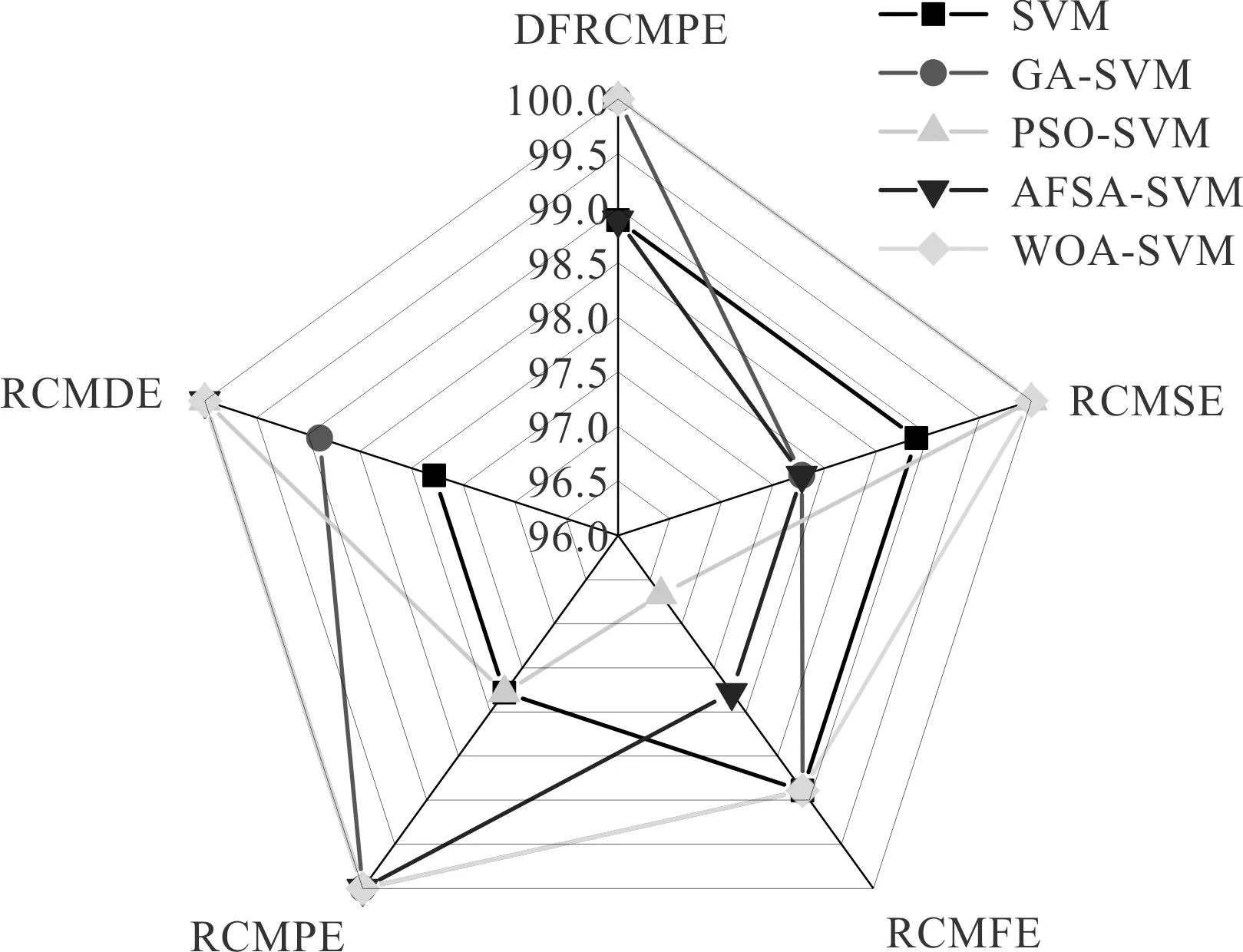
图11 不同分类器的损伤识别结果

由图11可知:在使用不同特征进行分类时,笔者所采用的WOA-SVM分类器都取了最佳的识别结果,优于其他几类分类器,证明其在处理损伤识别中的有效性;相对于其他特征提取方法,基于DFRCMPE方法的识别结果更优,这再一次证明了该方法的优越性和有效性;

此外,笔者发现未优化的SVM性能不稳定,这证明参数的设置对性能的影响非常大,证明了参数优化的必要性。

4 结束语

针对齿轮箱的损伤特征提取和损伤识别问题,笔者提出了一种基于DFRCMPE和WOA-SVM的集损伤特征提取和分类识别的齿轮箱损伤检测方法。笔者基于齿轮箱损伤实验采集的损伤数据,对该方法进行了实验,得出以下结论:

1)DFRCMPE结合了WPD能够提取信号低频、高频信息以及RCMPE性能稳定的特点,能够从齿轮箱振动信号中提取出高质量的损伤特征。分类器的验证结果也证明DFRCMPE优于RCMSE、RCMFE、RCMPE和RCMDE方法;

2)WOA-SVM具有优异的泛化性和优越的性能,在处理分类问题中优于GA-SVM、PSO-SVM、AFSA-SVM和SVM,证明其可在模式识别领域中获得较好的结果;

3)基于DFRCMPE和WOA-SVM的齿轮箱损伤识别方法取得了不错的识别结果,在识别齿轮箱的6种损伤类型中取得了100%的平均识别准确率。同时,在样本数量过少时,基于DFRCMPE和WOA-SVM的齿轮箱损伤识别方法也取得了最佳的损伤识别结果。

基于DFRCMPE和WOA-SVM的齿轮箱损伤识别方法可以用于有效地识别齿轮箱的故障类型,但其特征数量较多,导致分类效率较低。笔者后续将引入特征降维来缩小其特征维数。