基于数据驱动的离心泵转速识别及故障诊断研究*
王建平,杨 磊,张欣瑞,陈慧萍,牛会钊,宋 健,周同星
(1.新疆油田公司油气储运分公司,新疆 昌吉 831100;2.北京雅丹石油技术开发有限公司,北京 102200;3.安徽智寰科技有限公司,安徽 合肥 230601)
0 引 言
随着科学技术的进步,机械生产设备也向着高速运行、高强度连续工作的方向发展。但是,机械设备实际工作过程中难免会出现各种各样的问题,如系统误差、操作不当、设备损耗、系统老化等,轻则使得机器停机,重则造成人员伤亡等严重后果[1,2]。
旋转设备在整个机械设备领域有着举足轻重的地位,对该类部件进行状态监测与故障诊断显得尤为重要[3,4]。
在众多广泛应用旋转机械的行业中,石油、煤炭、风电、化工、钢铁等行业[5-9]由于特殊的应用场合和应用需求,设备大多需要24 h不停机,且基本上都处于无人值守的状态。这样的工况对设备的在线监测系统要求更高,所以对原场景影响小、安装部署方便、施工简单、易于快速上云和边缘计算实时反馈等需求的无线监测系统[10]备受青睐。
目前,行业中通常会采用振动或声音传感器采集由于损伤冲击而产生的信号(例如振动信号、位移信号、声音信号等),通过分析信号中这种阻尼衰减冲击响应的周期,判断当前零部件是否出现了某种类型的故障[11]。而在信号的实际冲击周期与设备故障特征匹配过程中,需要知道设备的转速,才能形成对应关系。这就需要获取设备当前的转速信息,一方面判断设备当前处于停机还是运行状态,以提高数据的有效性;另一方面根据转速信息计算出旋转设备故障特征,以进行诊断分析[12,13]。
现阶段,工业上常用的转速获取方式大体可以分为两类:加装转速传感器,直接采集转速数据;或者采用数据驱动方法,根据振动等信号识别转速。但第一种方法受成本、施工难度以及无线系统中转速测量情况等限制,越来越多的企业、学者倾向于采用第二种方法来获取设备的转速信息。
张帅等人[14]提出了一种基于希尔波特包络和自相关的转速识别方法,采用希尔伯特包络和三次自相关,对信号进行了时域分析,计算了短时窗内的发动机转速,根据移窗法得到了连续的发动机转速;虽然这种方法的精度和时间分辨率高,但是当信号具有较多的低频噪声时,容易在自相关运算时出现误识别,使结果出现偏差。冯坤等人[15]提出了一种基于转速提取和优化调制信号双谱(modulated signal bispectrum,MSB)的滚动轴承故障诊断方法,能够有效提取变转速齿轮箱滚动轴承的故障特征阶次,从而对滚动轴承进行有效的故障诊断;但该方法在信号低频噪声较多时,也容易出现识别偏差。徐炜卿等人[16]提出了一种基于快速傅里叶变换(fast Fourier transform,FFT)与离散傅里叶变换(discrete Fourier transform,DFT)相结合的频域分析方法,对采集到的汽车振动信号进行了分析,从而提取出了发动机的转速信息;但频谱的轴不对中、不平衡等问题会导致二倍甚至高倍转频能量高,这些情况将导致转速提取结果错误。
针对这些问题和现有方法的不足,笔者提出一种完全基于数据驱动的离心泵转速识别模型。
模型采用FFT计算得到振动信号的复频谱,然后利用有效频段内的频谱计算等效速度谱,计算速度谱的谱峰值与本底能量之间的差值,获取差值最大值,并与当前本底能量进行对比,若满足条件,其对应的频率即为设备的转频;在准确获得转频的基础上,再对信号进行包络解调,识别出故障频率以及边带特征,从而进行具体的故障诊断与处理。
1 数据驱动转速识别诊断模型
1.1 振动信号的快速傅里叶变换
快速傅里叶变换(FFT)是与离散傅里叶变换(DFT)的一种快速算法,这种方法分析了DFT中的多余运算,消除了重复运算,可大大节省运算的工作量。
离散数据信号经过FFT变换,其结果也为相同数目的复数点,可得到对应的复频谱。
传感器采集的原始离心泵振动信号x[n]如下:
x[n](n=0,1,2,…,N-1)
(1)
式中:N为信号长度;n为每一个序列点。
利用FFT计算得到原始振动信号的复频谱Px[k]如下:
(2)
式中:i为序数单位;e为自然对数函数的底数。
1.2 等效速度实谱的算法模型
先根据原始振动信号长度N和信号采样频率Fs,计算得到频谱对应的频率数组f[k]。
具体的对应关系如下:
(3)
根据式(3),将Px[k]转换成对应的Px[f]。对于离心泵等旋转设备,其基频一般在100 Hz以下;同时,为了防止噪声对基频识别的影响,需要过滤掉4 Hz以下的噪声。综上所述,笔者把复频谱中处于频率段[4 Hz,100 Hz]之间的成分筛选出来,得到有效信号复频谱PxValue[f]。
采用有效信号复频谱PxValue[f]和频率数组,计算出信号的等效速度实谱PxVel[f],即:
PxVel[f]=|-i×PxValue[f]/f|
(4)
1.3 速度谱峰值数组与本底能量的算法模型
为了消除底噪和误信号对转速特征提取的影响,笔者提取PxVel[f]中的峰值数组和本底能量。
其具体步骤如下:
1)对PxVel[f]进行差分计算,得到反映频谱能量变化的差分数组Diff[f];
2)针对数组中的每个点Diff[i],找出满足如下关系式的点集合:
(5)
3)找到全部满足式(5)条件的点集合,由PxVel[f]构建出峰值数组Px_VPeak[f];
4)对峰值数组Px_VPeak[f]进行中值滤波,筛选掉高频的峰值能量,得到速度谱的本底能量Px_Base[f]。
1.4 输出转频的算法模型
在速度谱中,转频对应的能量应高于其他频率对应的能量,并且相对于底噪有极高的信噪比,所以需要计算比较峰值数组能量和本底能量的差值数组Differ[f]:
Differ[f]=Px_VPeak[f]-Px_Base[f]
(6)
在差值数组Differ[f]中,定位到差值最大值对应的频率f0以及差值最大值Differ[f0],可以得到最终的转频Frpm:
Frpm=f0
(7)
1.5 故障诊断模型及流程
获得设备的转频Frpm之后,可结合包络解调和故障频率匹配的方法,对设备的故障频率进行计算分析,进行故障诊断。
故障诊断的流程如图1所示:
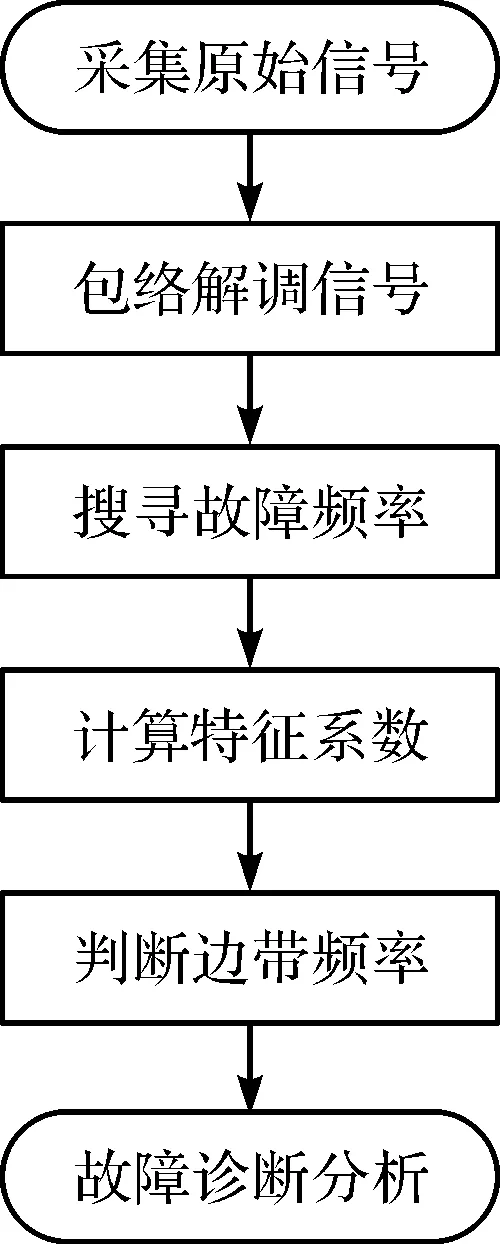
图1 故障诊断分析流程图
其中,图1中的包络解调步骤如下:
对采集到的信号x[n]进行余弦表达得到实部xm(t):
xm(t)=Am[1+αmcos(2πfmt)]cos(2πfzt)
(8)
式中:Am为调制信号的幅值;am为调制系数;fm为调制频率;t为时间。
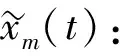
(9)
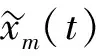
(10)
对所述解析信号Zm(t)取绝对值得到包络信号:
(11)
对所述包络信号进行快速傅里叶变换,得到对应的复频谱PF[f]:
PF(f)=FFT(Am|1+αmcos(2πfmt)|)
(12)
其中,FFT为快速傅里叶变换的计算函数。
然后在复频谱PF[f]的低频段中,搜寻具有明显谐波特征的频率,若存在符合的故障频率fw,则进一步计算该故障频率fw和转频Frpm对应的特征系数i:
(13)
再判断故障频率fw周围是否存在边带,综合考虑特征系数i数值范围和边带特征,可以判断出故障出现的具体位置及故障原因。
2 实验与结果分析
2.1 实验
为了对上述算法模型的准确性进行验证,笔者采用2个实际案例对模型和算法过程进行详细验证,并基于工业现场实际的离心泵振动数据进行计算分析。
2.1.1 轴承故障信号转速分析
笔者将加速度传感器安装于离心泵的表面,以采样频率Fs=51 000 Hz进行采样,得到振动信号x[n],采样长度N=32 768。
原始信号的波形与频谱如图2所示。
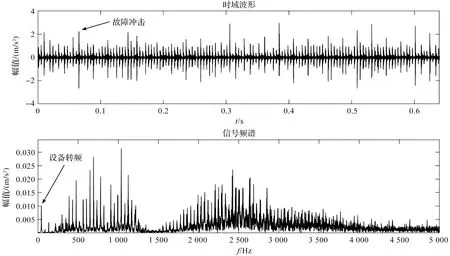
图2 原始信号的波形与频谱
从图2的时域波形上可以看到,该离心泵信号带有明显的周期性冲击。
该实例采集的设备带有轴承内圈故障特征,接下来采取笔者提出的算法模型进行计算分析:
1)从图2的信号频谱可知:大部分的频率均为包含了内圈故障调制的频率成分,从频谱图中可以看出在低频段存在一个约为43.58 Hz的峰值,实际上即为设备的旋转频率(2 600 r/min),但是在没有先验知识的前提下,采用常规的频谱峰值提取难以获取设备的转速信息;
2)经过频率筛选、频域变换,获得原始信号的等效速度实频谱。
等效速度实频谱如图3所示。
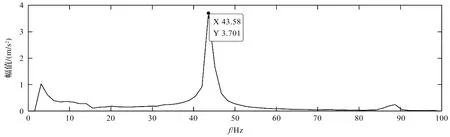
图3 等效速度实频谱
从图3可知:设备的转频分量得到了有效保留和放大;
3)对速度实频谱分别进行中值滤波和峰值提取,得到速度谱本底能量和速度谱峰值分布。
速度谱本底能量和速度谱峰值如图4所示。
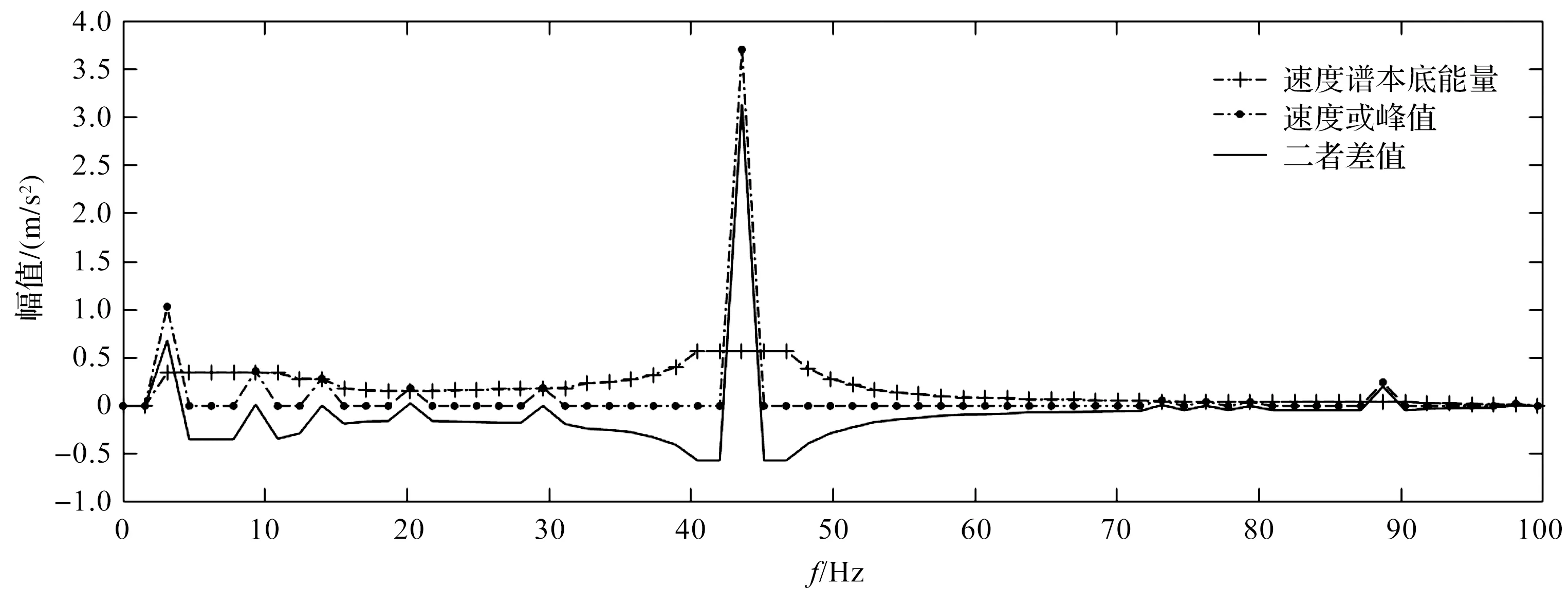
图4 速度谱本底能量和速度谱峰值
计算图4速度谱本底能量与速度谱峰值的差值,得到差值最大点对应的频率43.58 Hz,即为设备当前的旋转频率。
2.1.2 噪声信号转速分析
将加速度传感器安装于故障离心泵的表面,以采样频率Fs=12 000 Hz进行采样,得到振动信号x[n],采样长度N=16 384。
原始信号的波形与频谱如图5所示。
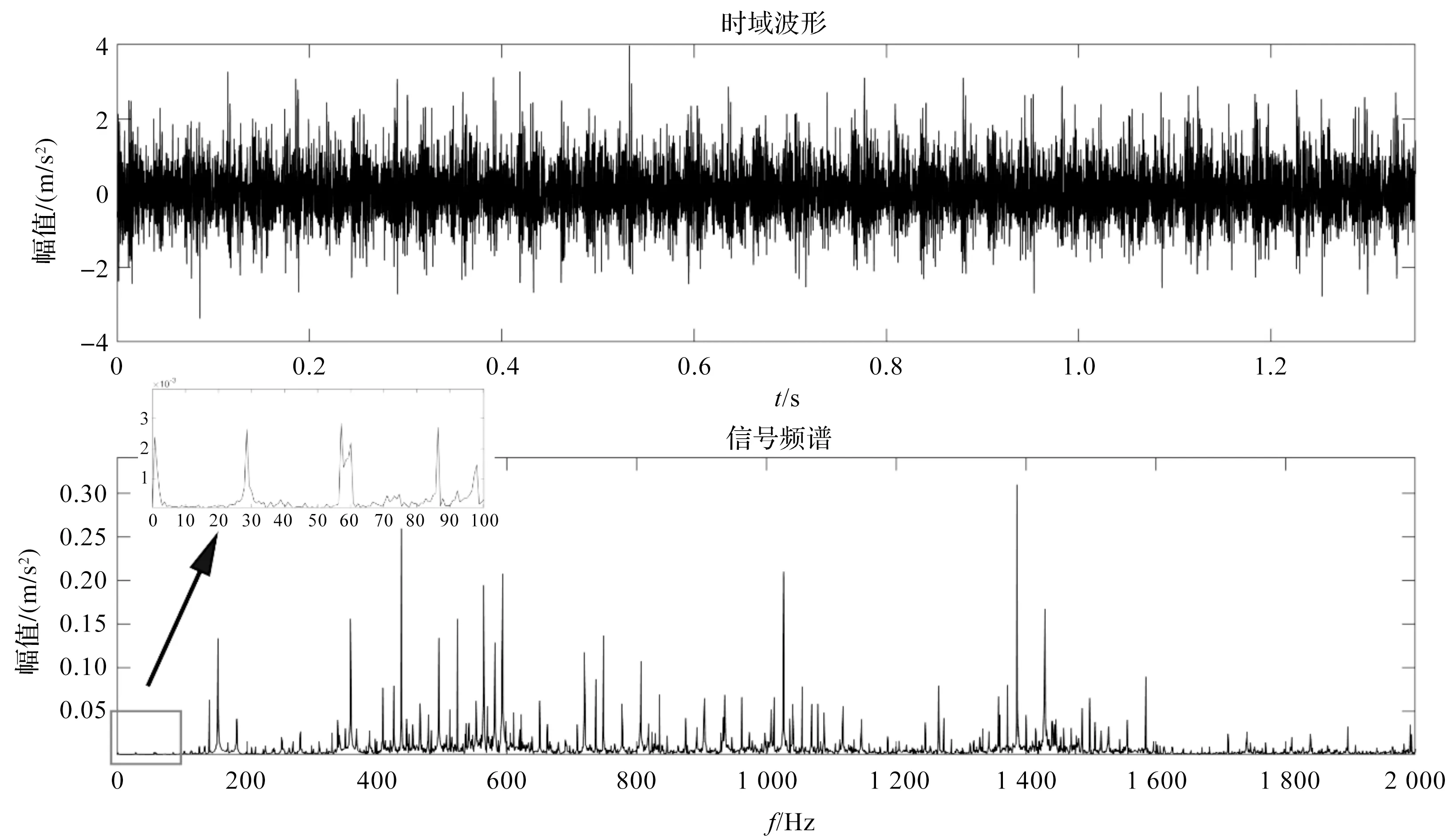
图5 原始信号的波形与频谱
由图5的时域波形可知:该离心泵信号故障冲击不明显,整体信号噪声水平较高,需采用笔者提出的算法模型进行计算分析:
1)由图5的信号频谱可知:由于高频段的频率成分丰富且能量较高,设备转频被完全淹没在低频段,而且其倍频能量较高,即使局部放大也无法准确判断设备转速;
2)计算原始振动信号的等效速度实频谱。
等效速度实频谱如图6所示。
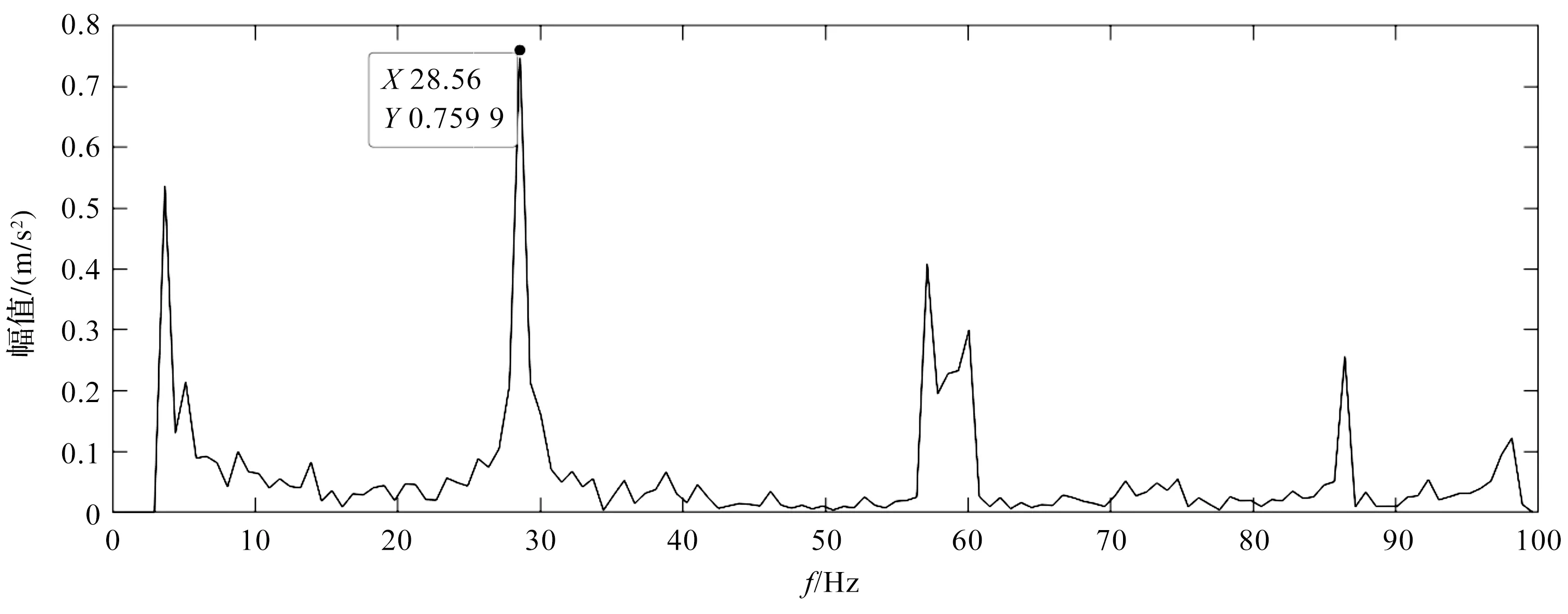
图6 等效速度实频谱
在图6中,可以观察到转频成分(28.56 Hz)被明显放大,但是低频段的干扰成分也同样被一定程度地放大;
3)对速度实频谱分别进行中值滤波和峰值提取,得到速度谱本底能量Px_Base[f]和速度谱峰值分布Px_VPeak[f]。
速度谱本底能量和速度谱峰值如图7所示。
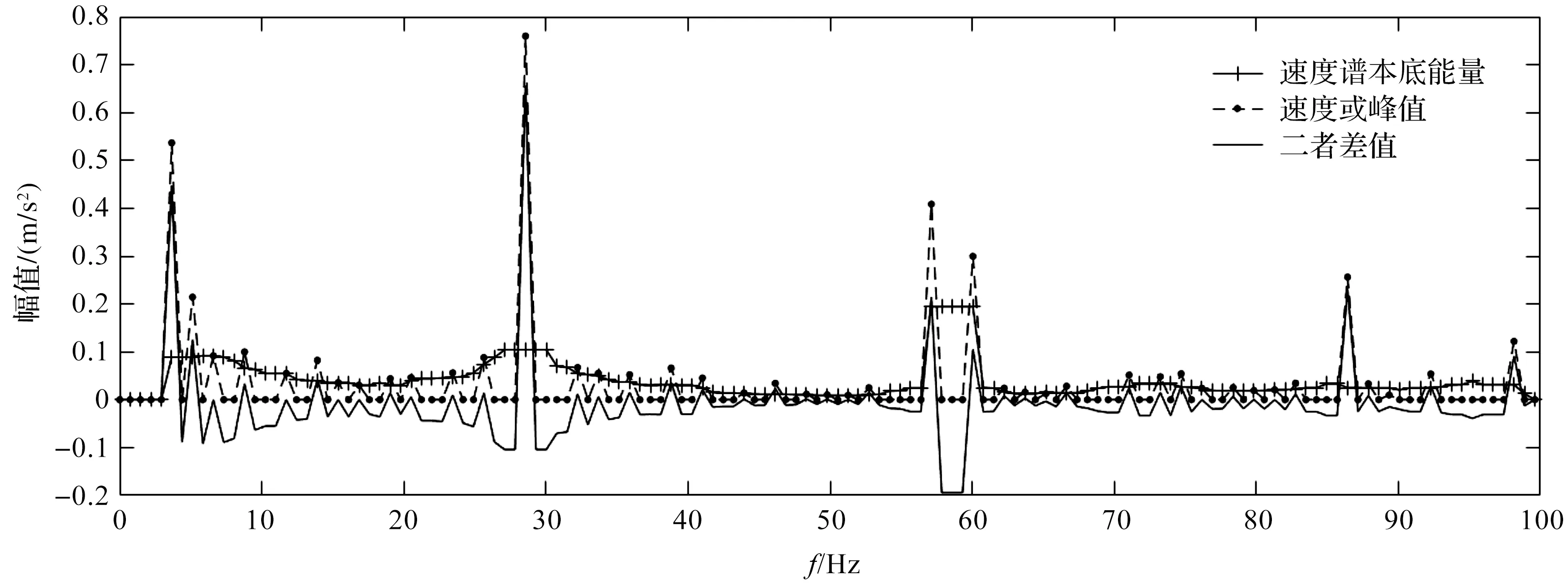
图7 速度谱本底能量和速度谱峰值
计算二者的差值得到差值最大点对应的f0=28.56 Hz,即为设备当前的旋转频率。
2.2 故障诊断结果分析
根据以上2个实际案例分析,笔者发现该转速识别模型能准确识别出两种不同离心泵振动数据的转频成分。
案例1中的离心泵有轴承内圈故障,振动数据带有明显的周期性冲击,在低频段分析其等效速度实频谱时,能够清楚得到其转频成分。
案例2中的离心泵信号故障冲击不明显,但整体信号噪声水平较高,所以在低频段分析其等效速度实频谱时,各种冲击错误信号较多。
采用算法模型对峰值能量和本地能量进行对比,选取差值最大的点,即转频。根据先验知识进行验证,证明采取谱峰值数组与本底能量的算法模型可以准确计算出设备的转频成分。
笔者准确识别出离心泵的转频成分后,再结合故障特征频率与转频的对应关系,可进行后续的故障诊断。笔者整理出常见的滚动轴承内圈、外圈、滚动体故障信号对应的特征。
轴承故障类型及对应参考系数如表1所示。
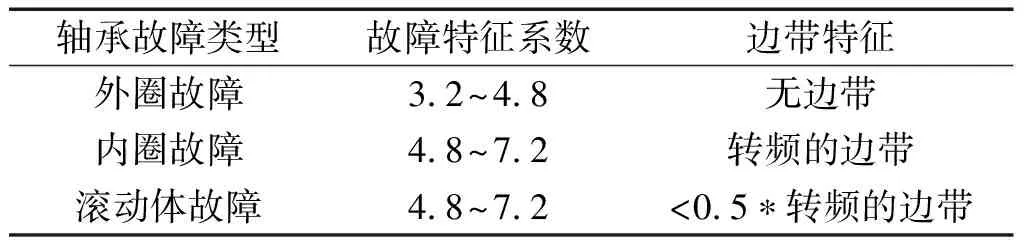
表1 轴承故障类型及对应参考系数
根据表1中的故障特征系数范围,笔者大致判断轴承的故障类型,并对案例1中的故障信号进行包络解调[17],得到包络谱。
故障信号的包络谱如图8所示。
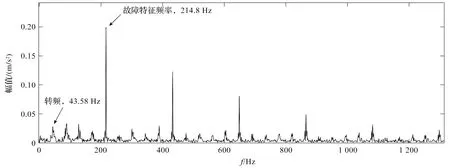
图8 故障信号的包络谱
笔者识别该离心泵的转频为43.58 Hz,在包络谱中,能看到明显的故障特征频率为214.8 Hz,并且故障特征频率周边有间隔为43.58 Hz的冲击边带,符合轴承内圈故障的频率分布特征。
笔者计算其轴承内圈故障系数(ball pass frequency of the inner race,BPFI),即:BPFI=214.8÷43.58=4.93。
该轴承内圈故障系数BPFI和实际轴承内圈故障系数4.93一致,也和表1中的故障特征系数和边带特征相吻合。
以上结果说明,采取笔者提出的模型进行转频识别以及故障诊断,其结果和实际结果相符合。
3 结束语
在提取离心泵的转速数据时,存在数据提取成本高、操作困难,以及获得的先验参数误差较大等问题,为此,笔者提出了一种完全基于数据驱动的离心泵转速识别模型。
笔者采用计算速度谱的谱峰值与本底能量之间的最大差值来判断设备转频,采取包络谱解调的方法识别离心泵的故障特征,并根据实际的离心泵振动数据,对上述算法模型的准确性进行了验证。
研究结果表明:
1)对于带有明显周期性冲击的故障信号,在低频段分析其等效速度实频谱时,能够清楚识别出其存在43.58 Hz的峰值,即设备的转频;
2)对于信号噪声水平较高的故障信号,通过计算速度谱的谱峰值与本底能量之间的差值,也能识别出差值最大的峰值点28.56 Hz,可有效避免速度谱计算过程中的低频干扰;
3)通过对故障信号的包络解调进行分析,可准确识别出故障频率、边带特征,计算出故障特征系数为4.93且存在43.58 Hz的冲击边带,判断出存在轴承内圈故障,和实际离心泵轴承故障情况一致。
对于变转速的设备,其低频段的转频成分可能不是最明显的峰值,以速度谱的谱峰值与本底能量之间的最大差值来判断转频成分可能会存在误差。如何对这些问题进行优化,这将是笔者后续的研究方向。

