空位缺陷和原子掺杂对氮化镓热导率影响的分子动力学模拟

高志乐 ,王继芬

(1.上海海事大学商船学院,上海 201306;2.上海第二工业大学 资源与环境工程学院,上海 201209)

近年来,由于氮化镓(GaN)具有电子饱和率高、击穿电压大、抗腐蚀性强、稳定性好等优点[1-2],基于GaN 材料的光电子器件[3]、高温大功率器件和高频微波器件[4]得到了广泛应用。目前设备中的绝大多数GaN 晶体是通过在基片上异质外延生长获得的[5],这些衬底与GaN 之间的晶格常数和热膨胀系数存在着不同程度的不匹配,导致了实际制得的GaN 存在很多缺陷[6],如空位缺陷和原子掺杂。缺陷的存在对GaN 的光学、电学和热学等相关性能有非常重要的影响[7],严重影响了GaN 基半导体设备的使用寿命、发光效率、电子迁移率以及热传导等各方面性能[8]。

实际应用中,GaN 往往存在空位缺陷及原子掺杂的情况,这是研究人员在研究GaN 时比较关注的。Cai 等[9]采用第一性原理计算研究了缺镓空位(VGa)和缺氮空位(VN)缺陷对GaN 电子结构和光学性质的影响,研究发现VGa 中价带向更高能量区域移动,VN 中价带和导带明显向低能区移动。空位缺陷的存在导致GaN 的带隙增大,使得GaN 的光学性质发生了改变。Abdalla 等[10]利用第一性原理系统研究了Fe 掺杂对纤锌矿型GaN 电子和磁性的影响。研究发现,当Fe 原子在Ga 位置掺杂时,GaN 由半导体状态转变为磁性半导体状态,从而导致Ga 位Fe 掺杂的GaN 比N位Fe 掺杂的GaN 更稳定。Beechem 等[11]通过时域热反射率研究了n 型和p 型掺杂的GaN 的热导率,结果显示,当GaN 厚度增大时,n 型GaN 的热导率几乎恒定,而p 型GaN 的热导率会出现下降的趋势。Jezowski 等[12]通过实验研究了掺杂的自由载流子对GaN 晶体中声子散射的贡献,实验结果表明,通过电场影响了声子的散射率、键硬度和离子性以及晶体对称性,从而明显改变了GaN 的热导率。为了解决空位缺陷和原子掺杂给GaN 材料性能带来的影响,需要进一步了解GaN 空位缺陷和原子掺杂的基本特性及其变化规律。

本文利用非平衡分子动力学(NEMD)的方法研究了空位缺陷和原子掺杂等缺陷对GaN 热导率的影响,介绍了GaN 势函数的选取以及模拟计算过程主要的参数设置;对GaN 的完整结构、空位缺陷结构以及原子掺杂结构的计算结果进行了分析与讨论。该研究可为GaN 材料器件的热管理应用提供一定的理论参考。

1 模拟模型和计算方法

1.1 GaN 及其空位缺陷和原子掺杂结构

GaN 晶体通常有纤锌矿(WZ)、闪锌矿(ZB)和岩盐矿(RS)三种结构,如图1 所示。因为WZ 结构的GaN 是稳定的,ZB 结构的GaN 是易变的,而RS 结构GaN 只在高压情况下才会出现,所以GaN 晶体通常为WZ 结构,其单元格对应的空间群结构为P63mc(C46V)。本文中,以WZ 结构的GaN 作为研究对象,讨论了空位缺陷和原子掺杂对GaN 的C 面(0001)方向热导率影响。

图1 (a) 纤锌矿结构;(b) 闪锌矿结构;(c) 岩盐矿结构Fig.1 (a) WZ structure;(b) ZB structure;(c) RS structure

研究表明,空位缺陷是GaN 的本征缺陷。VGa 是在禁带附近引入自旋极化缺陷态的受主缺陷;VN 是一种施主缺陷,它导致费米能级的升高。GaN 结构中的本征空位点缺陷将引起低能区附近光学性质的显著变化[9]。有研究显示GaN 中掺杂Fe,将在GaN 结构中形成一个深受体中心,和一些电子生成的内在缺陷补偿通过机动的孔,从而赋予GaN 材料高电阻特性[13]。除了Fe 的掺杂,Mg 和Si 也是GaN 晶体中的重要掺杂剂。Mg 是实现p 型GaN 导电性的唯一掺杂剂[14],Si 是实现n 型GaN 掺杂的重要掺杂剂,能有效提高发光效率[15]。GaN 的p 型和n 型掺杂是制备光电子器件的关键。

GaN 含有空位缺陷的结构如图2 所示,包含了16 个Ga 原子和16 个N 原子的2×2×2 超晶胞模型。图2 (a)、(b)和(c)分别是完整GaN、VGa-GaN 和VN-GaN,相应的系统分别是Ga16N16、Ga15N16 和Ga16N15。

图2 (a) 无空位;(b) 缺镓空位;(c) 缺氮空位Fig.2 (a) No vacancies;(b) VGa;(c) VN

GaN 含有原子掺杂的结构如图3 所示,包含了16 个Ga 原子和16 个N 原子的2×2×2 超晶胞模型。Fe、Mg、Si 原子以3.13%的掺杂率直接取代超胞中的一个Ga 原子。相应的系统分别是Ga15Fe1N16、Ga15Mg1N16和Ga15Si1N16。

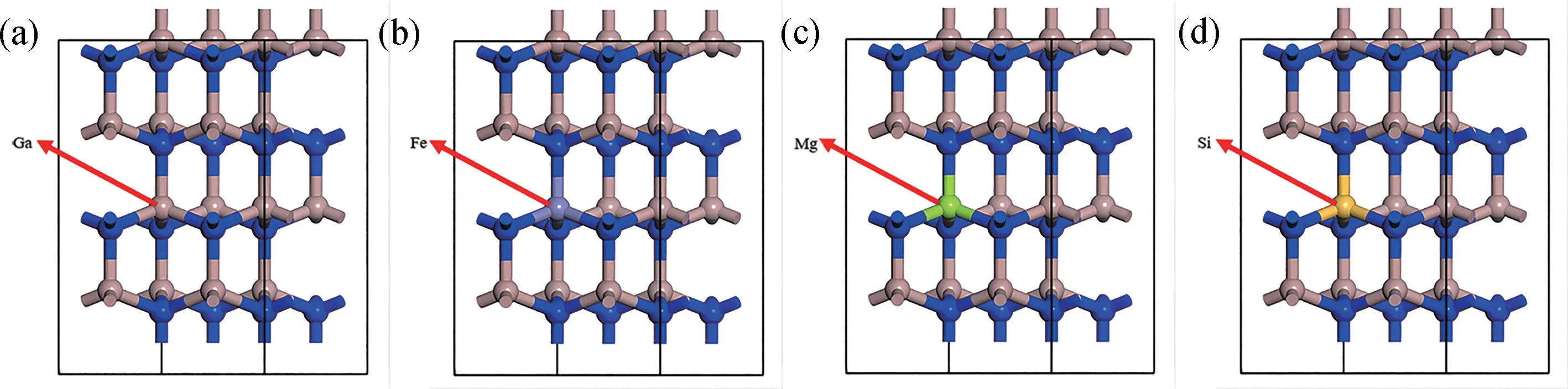
图3 (a)无掺杂;(b) Fe 掺杂;(c) Mg 掺杂;(d) Si 掺杂Fig.3 (a) No doping;(b) Fe-doping;(c) Mg-doping;(d) Si-doping

1.2 非平衡分子动力学模拟

因NEMD 的原理与实验测量相似,本文利用NEMD 的方法模拟计算GaN 的传热性能。计算时,通过热浴的方法建立了热源与热汇两个区域,在两个区域之间有热流通过并且产生稳定的温度梯度。根据傅立叶的热传导定律计算GaN 的热导率。

式中:Q,A,和k分别是热流速率、横截面积、温度梯度和热导率。能量从热源流向热汇的横截面积表示如下:

式中:W是模型在X方向的长度;δ是模型在Y方向的长度。本文在计算过程中利用定热流的方法来产生稳定的温度梯度。

1.3 计算模型

图4 为采用NEMD 方法计算GaN 热导率的模型示意图。Z轴方向设定为计算热导率的方向与GaN 初始晶胞的(0001)方向相对应。X和Y方向设定为周期性边界条件。传热的Z方向设定为可收缩性边界条件。在两端各设置一个1.4 nm 的绝热区域,以防模拟过程中的原子溢出。热浴的宽度为4 nm,热传导区域的长度为52 nm,在GaN 的声子自由程范围内[16]。

图4 计算模型区域划分Fig.4 Area divisions of Calculation model

模拟计算中,时间步长设置为1 fs,热源与热汇之间设定一个恒定的热流(q=0.5 eV/ps)。其中,系统中的原子在某一时刻的温度可以表示如下:

式中:T是原子的温度;m是原子的质量;Vi是i原子的速度;Nl是原子的总数;KB是玻尔兹曼常数。模拟计算时沿着传热方向将传导区域平均分成40 块,统计每块内原子的平均温度,从而得到GaN 晶体的热源和热汇之间沿传热方向的温度分布。

声子态密度(PDOS)和声子参与率(PPR) 都是表征材料中声子活动的有效方法。通过对PDOS 和PPR 的研究,分析空位缺陷和原子掺杂对GaN 的声子输运特性的影响。PDOS 是通过速度自相关函数(VACF)的傅立叶变换得到[17]。

式中:PDOS(ω) 表示为振动频率为ω时的总PDOS,其VACF 由公式(5)表示[18]。

式中:Vi(t) 是粒子i在t时刻的速度矢量;N是原子总数;〈 〉是尖括号,表示集合平均;VACF(t) 是原子速度自相关函数。

计算GaN 的PPR 时,定义为[19]:

式中:N是原子总数;PDOSi(ω) 表示通过计算单粒子的VACF,得到的单粒子的PDOS。

1.4 势函数

本文分别利用Stillinger-Weber (SW)势函数[20]和Tersoff 势函数[21-22]计算了完整GaN 的PDOS,计算结果如图5 所示。结果表明利用SW 势和Tersoff 势得到的PDOS 在低频段0～10 THz 范围内吻合得比较好,在高频段20～30 THz 范围内,SW 势态密度频率比Tersoff 势态密度频率稍微偏大。通过图5 可以发现,完整GaN 在SW 和Tersoff 两种势函数下得到的PDOS 相差不大。考虑到本文涉及了GaN 的空位缺陷和原子掺杂等晶体缺陷,SW 势函数更适合GaN 晶体缺陷的情况,因此本文采用SW 势函数作为计算过程中原子间的作用力函数,其参数是采用Béré 和Serra[23]校正后的值。

图5 SW 和Tersoff 势函数下完整GaN 的PDOS 对比Fig.5 PDOS of intact GaN obtained by SW potential and Tersoff potential

2 结果与讨论

2.1 模型收敛性

对空位缺陷和原子掺杂GaN 结构进行模拟计算后,通过VACF[18]得到了各个GaN 模型的收敛性,如图6 (a)～(f)所示分别为完整GaN、VGa-GaN、VNGaN 和GaN 掺杂Fe、Mg、Si 原子模型的收敛性图。

图6 (a) 完整GaN 收敛性;(b) VGa-GaN 收敛性;(c) VN-GaN 收敛性;(d) Fe 掺杂GaN 收敛性;(e) Mg 掺杂GaN 收敛性;(f) Si 掺杂GaN 收敛性Fig.6 (a) Convergence of intact GaN;(b) Convergence of VGa;(c) Convergence of VN;(d) Convergence of Fe-doped GaN;(e) Convergence of Mg-doped GaN;(f) Convergence of Si-doped GaN

通过图6(a)～(f)可以发现,VACF 在初始阶段都会有剧烈的波动,当后期时间趋近于3 ps 时,可以发现VACF 的振荡减缓,趋近于0。根据图6(a)～(f)可知,不同结构GaN 模型的收敛性在3 ps 附近的振荡幅度不同。这是因为它们的结构存在着差异,从而导致他们收敛性的不同展现,这并不影响热导率的计算[24-25]。通过图6 可以证明在本文的模拟计算条件下,这六种结构的GaN 都能够得到相当精确的热导率值。

2.2 GaN 晶体的热导率

利用NEMD 方法计算GaN 热导率,得到如图7 所示的热源和热汇之间良好的温度梯度分布。通过图7可以发现,忽略热源和热汇附近的非线性区域,GaN体系的温度趋于线性分布。通过拟合热源和热汇之间的线性区域确定了GaN 体系的温度梯度。根据公式(1)和(2)可得到GaN 传热区长度为52 nm 时的热导率。

图7 GaN 体系温度分布图Fig.7 GaN system temperature distribution chart

考虑垂直传热方向的尺寸效应,当GaN 沿传热方向的体系长度都为52 nm 时,计算得到不同截面积的GaN 热导率如表1 所示。

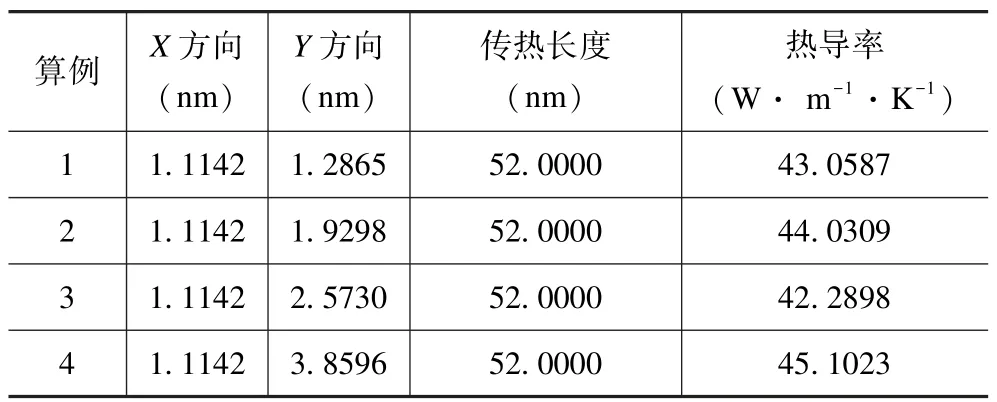
表1 GaN 不同截面尺寸时的热导率Tab.1 Thermal conductivity of GaN at different section sizes

通过表1 发现,四个GaN 算例的热导率属于同一数量级。当X方向尺寸不变,Y方向尺寸分别为1.2865,1.9298,2.5730 和3.8596 nm 时,可以发现GaN 热导率的变化很小,最大值45.1 W·m-1·K-1与最小值42.3 W·m-1·K-1之间相差约2.8 W·m-1·K-1。按样品重复误差分析,则平均值约为43.7 W·m-1·K-1,体系误差为±1.5 W·m-1·K-1,即3.4%。因此当使用NEMD 方法计算GaN (0001)方向的热导率时,X和Y方向尺寸对结果有较小的影响,在精度要求不高时,可以不予考虑。

2.3 空位缺陷对GaN 热导率的影响

图8 所示是完整GaN、VGa-GaN 和VN-GaN 的热导率在300～600 K 温度范围内的变化趋势。通过图8 可以发现,当温度从300 K 变化到600 K 时,三种结构GaN 的热导率都随着温度的升高呈下降趋势。完整GaN 热导率的下降速率快于VGa-GaN 和VN-GaN 热导率的下降速率。这表明完整GaN 的热导率和含有空位缺陷结构的GaN 热导率对于温度依赖性的一般趋势都是随着温度的升高而减小,且完整GaN 的热导率对温度的依赖性更大。根据图8 可知,当温度为300 K时,完整GaN 的热导率最大为43.06 W·m-1·K-1。VGa-GaN 和VN-GaN 的热导率与完整GaN 的热导率相比会出现较大的下降,但VGa 缺陷与VN 缺陷的GaN 热导率相差不大,分别为10.83 W·m-1·K-1和8.66 W·m-1·K-1,与完整GaN 的热导率相比分别下降74.85%和79.89%。这表明GaN 空位缺陷的存在对GaN 热导率的影响较大。

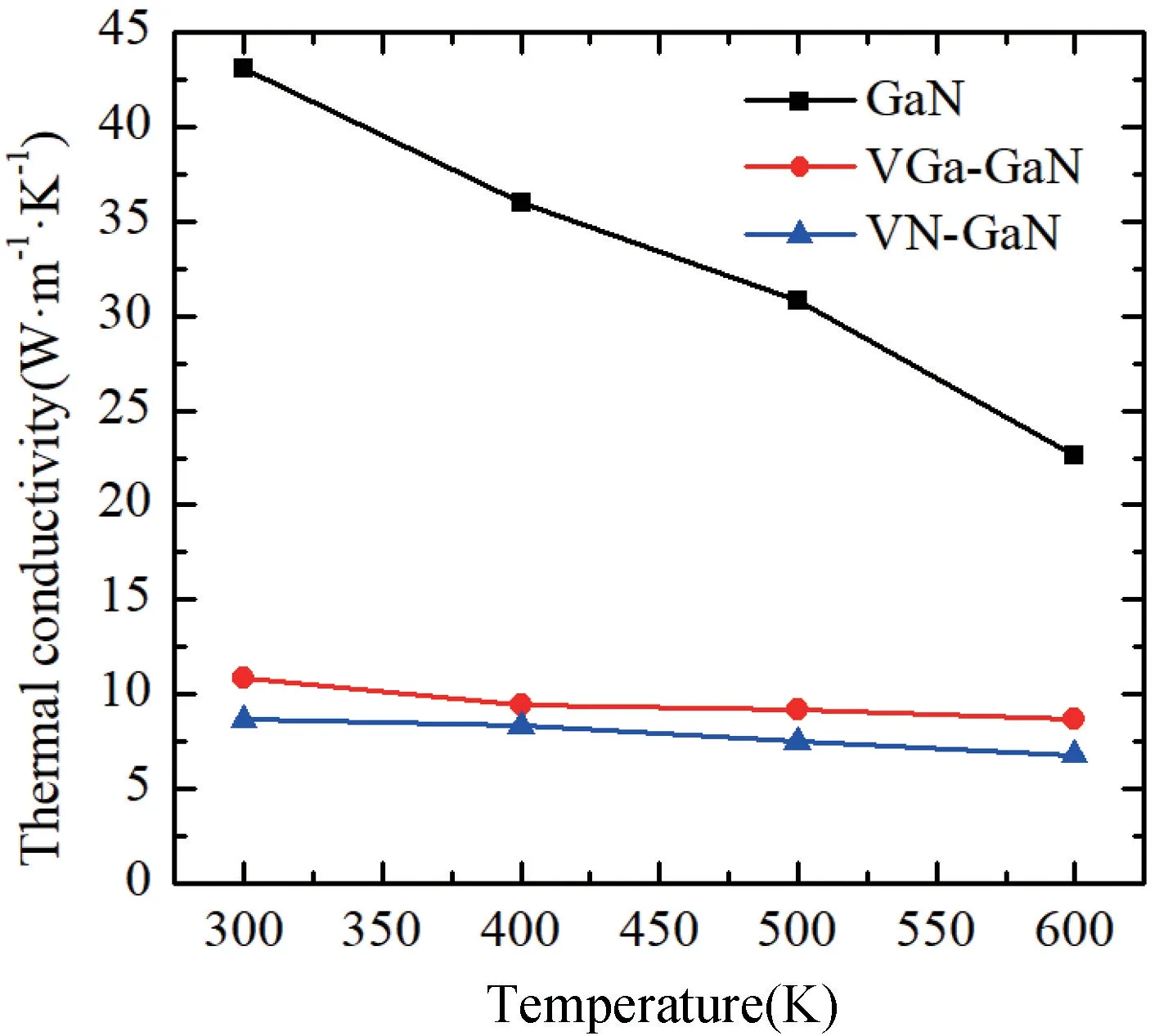
图8 完整GaN 与含空位缺陷GaN 的热导率对比Fig.8 Thermal conductivity of intact GaN compared to GaN with vacancy defects

为了解空位缺陷对GaN 热传输机理的影响,计算了300 K 时完整GaN、VGa-GaN 和VN-GaN 相关的PDOS,如图9 (a)～(d) 所示。

图9 (a) 300 K 时完整GaN 各原子的PDOS;(b) 300 K 时完整GaN 与两种空位缺陷GaN 的Ga 原子PDOS 对比;(c) 300 K 时完整GaN 与两种空位缺陷GaN 的N 原子PDOS 对比;(d) 300 K时完整GaN 与两种空位缺陷GaN 的PDOS 对比Fig.9 (a)PDOS for each atom of intact GaN at 300 K;(b) Comparison of Ga atomic PDOS between intact GaN and two vacancy-deficient GaN at 300 K;(c) Comparison of N atomic PDOS between intact GaN and two vacancy-deficient GaN at 300 K;(d) Comparison of PDOS between intact GaN and two vacancy-deficient GaN at 300 K

通过图9(a)可以发现,Ga 原子的振动峰在低频区域(5～10 THz)具有较高的峰值,而N 原子的振动峰在高频区域(20～30 THz)具有较高的峰值。图9(a)的现象说明GaN 结构中的低频声子主要是Ga 原子起主要作用,高频声子主要是N 原子起主要作用,这和原子质量的相互作用是一致的。通过图9(b)和(c)可以发现,在相同的条件下,完整GaN、VGa-GaN 和VN-GaN 中的Ga 原子与N 原子在低频区域和高频区域都存在着振动峰,且Ga 原子的低频振动峰值高于高频振动峰值,而N 原子的高频振动峰值高于低频振动峰值。根据图9(d)可知,300 K 时,三种结构GaN的PDOS 曲线都在低频区域和高频区域存在着振动峰,但VGa-GaN 的PDOS 有一点特殊,它在15.2 THz 有一个振动峰。由于GaN 的热导率主要受低频区域声子的影响[26],所以重点分析了低频区域的声子态密度。通过分析图9(d)发现,在5.3 THz 处存在着一个振动峰,在这个振动峰处完整GaN 的PDOS 值＞VGa-GaN的PDOS 值＞VN-GaN 的PDOS 值。出现这种变化趋势是因为当GaN 结构中出现空位缺陷时,GaN 结构中参与热输运的声子数量减少了,根据经典晶格传热理论,声子数量的减少导致了GaN 结构中声子群速度的下降[27-28],同时VN-GaN 的费米能级高于VGa-GaN的费米能级。因此同一条件下,完整GaN 的热导率高于VGa-GaN 和VN-GaN 的热导率,VGa-GaN 的热导率高于VN-GaN 的热导率。

如图10 所示,是计算得到的完整GaN、VGa-GaN和VN-GaN 在300 K 时的PPR。为实现声子局部化的概念,将局域状态定义为参与率小于0.2 的状态,而大于0.2 的部分设定为离域状态,这个定义将在整个研究中保持一致。通过图10 可以发现,在PPR 谱的左端(0～10 THz),声子处于离域状态,右端(55～65 THz)的声子处于局域状态。对GaN 热传输有主要贡献的声子来自离域状态[17]。其中低频区域(0～10 THz)的声子主要是声学模式,高频区域(55～65 THz)的声子则是光学模式。根据图10 可知,无论是在低频区域还是在高频区域,PPR 谱都遵循倒U 形,不同结构GaN 的离域状态大都落在相同的区域中。这说明空位缺陷对GaN 热传输时PPR 的影响并不大,即PPR并不是导致GaN 热导率随着空位缺陷出现而下降的主因。

图10 300 K 时完整GaN 与含空位缺陷GaN 的PPR 对比Fig.10 PPR of intact GaN compared to GaN with vacancy defects at 300 K

2.4 原子掺杂对GaN 热导率的影响

如图11 所示,是完整GaN、Fe 掺杂GaN、Mg 掺杂GaN 和Si 掺杂GaN 的热导率在300～600 K 温度范围内的变化趋势。根据图11 可知,当温度从300 K 变化到600 K 时,四种结构GaN 的热导率随着温度的升高均呈下降趋势。完整GaN 的热导率下降速率快于GaN 掺杂结构的热导率下降速率,Fe 掺杂GaN 热导率的下降速率快于其他两种GaN 掺杂结构热导率的下降速率。这说明含有原子掺杂结构的GaN 热导率对于温度依赖性的一般趋势是随着温度的升高而减小。当温度为300 K 时,完整GaN 的热导率最大,为43.06 W·m-1·K-1。Fe 掺杂GaN、Mg 掺杂GaN 和Si 掺杂GaN 的热导率与完整GaN 的热导率相比会出现较大的下降。Fe 掺杂GaN、Mg 掺杂GaN 和Si 掺杂GaN 的热导率分别为10.15,8.22 和4.70 W·m-1·K-1,与完整GaN 的热导率相比分别下降76.43%,80.91%和89.08%。这表明完整GaN 原子经掺杂后,它的热传导性能会发生较大的改变。

图11 完整GaN 与原子掺杂GaN 的热导率对比Fig.11 Comparison of the thermal conductivity between intact GaN and atomically doped GaN

为了解原子掺杂对GaN 热传输机理的影响,计算了完整GaN 和原子掺杂GaN 结构在300 K 时的相关PDOS,如图12 (a)～(d) 所示。

图12 (a) 300 K 时完整GaN 与三种掺杂体系GaN 的PDOS 对比;(b) 300 K 时完整GaN 与三种掺杂体系GaN 的Ga 原子PDOS 对比;(c) 300 K 时完整GaN 与三种掺杂体系GaN 的N 原子PDOS 对比;(d) 300 K 时三种掺杂原子的PDOS 对比Fig.12 (a) Comparison of PDOS between intact GaN and three doping systems of GaN at 300 K;(b) Comparison of Ga atomic PDOS between intact GaN and three doping systems of GaN at 300 K;(c) Comparison of N atomic PDOS between intact GaN and three doping systems of GaN at 300 K;(d) Comparison of PDOS for three doped atoms at 300 K

通过图12(a)可以发现,300 K 时,这四种结构GaN 的PDOS 曲线具有相似的变化趋势,在低频区域(5～10 THz)和高频区域(20～30 THz)都存在着振动峰。通过分析图12(a)发现,在5.3 THz 和24.2 THz处存在振动峰,在两个振动峰处完整GaN 的PDOS 值＞Fe 掺杂GaN 的PDOS 值＞Mg 掺杂GaN 的PDOS 值＞Si 掺杂GaN 的PDOS 值。根据图12(b)和(c)可知,相同的条件下,完整GaN、Fe 掺杂GaN、Mg 掺杂GaN 和Si 掺杂GaN 中的Ga 原子与N 原子在低频区域和高频区域都存在着振动峰。Ga 原子的低频振动峰值高于高频振动峰值,而N 原子的高频振动峰值高于低频振动峰值。根据图12(d)可知,Fe 掺杂GaN、Mg掺杂GaN 和Si 掺杂GaN 中掺杂的原子在低频区域和高频区域都存在着振动峰,且掺杂原子的低频振动峰值高于高频振动峰值。出现上述的变化趋势是因为当完整GaN 结构中出现原子掺杂时,GaN 热输运时的声子散射现象增强了,参与热输运的声子数量减少,导致了GaN 结构中声子群速度的下降,从而导致PDOS峰值的下降。当完整GaN 掺杂Fe、Mg 和Si 后,声子在热传输过程中更容易散射,导致声子寿命降低。同时Fe 是磁性原子[29],在Fe 取代GaN 中的一部分Ga原子后,形成了比Mg 和Si 掺杂GaN 更稳定的磁性材料。另外由于Mg、Si 掺杂具有较强的声子非谐性,增强了声子-声子散射速率,而Si 掺杂相较于Mg 掺杂对于声子弛豫时间有更高的要求[30]。因此在相同条件下,完整GaN 的热导率＞Fe 掺杂GaN 的热导率＞Mg 掺杂GaN 的热导率＞Si 掺杂GaN 的热导率。

如图13 所示,对完整GaN 和原子掺杂GaN 结构中的声子性质进行了深入研究,计算了四种结构在300 K 时的PPR。为了实现声子局部化的概念,同样将局域状态定义为参与率小于0.2 的状态,而大于0.2的部分设定为离域状态。通过图13 可以发现,PPR 谱的左端(0～10 THz)声子处于离域状态,右端(55～65 THz)的声子处于局域状态。对GaN 热传输有主要贡献的声子来自离域状态[17]。其中低频区域(0～10 THz)声子主要是声学模式,高频区域(55～65 THz)的声子则是光学模式。无论是在低频区域还是在高频区域,PPR 谱都遵循倒U 形,不同结构的GaN 的离域状态大都落在相同的区域中。这说明完整的GaN 结构中出现原子掺杂时,PPR 对于GaN 的热导率并没有产生重要的影响,即PPR 并不是导致原子掺杂GaN 的热导率小于完整GaN 热导率的主因。

图13 300 K 时完整GaN 与原子掺杂GaN 的PPR 对比Fig.13 PPR of intact GaN compared to atomically doped GaN at 300 K

3 结论

本文基于NEMD 方法,利用SW 势函数研究了空位缺陷和原子掺杂对GaN 热导率的影响。得出以下结论:

(1) 当GaN 含有空位缺陷结构时,相同温度下,完整GaN 的热导率高于含有空位缺陷的GaN 热导率,且VGa-GaN 的热导率总高于VN-GaN 的热导率。

(2) 对于含有原子掺杂的GaN 结构,相同条件下,GaN 掺杂体系的热导率都低于完整GaN 的热导率。Fe 掺杂的GaN 热导率为GaN 三种掺杂结构中最高,Si 掺杂的GaN 热导率为GaN 三种掺杂结构中最低。

(3) 当温度从300 K 上升到600 K 时,完整GaN、含有空位缺陷GaN 与原子掺杂结构GaN 的热导率均会受到温度的影响,且随温度的上升呈下降趋势。