总温畸变下跨声压气机失速过程非定常模拟

赵红亮，张文强，邱佳慧，张敏，杜娟，*，聂超群

1．华北电力大学 能源动力与机械工程学院，北京 102206

2．北京理工大学 机电学院，北京 100081

3．中国科学院 工程热物理研究所 数字孪生研究中心，北京 100190

4．中国科学院 先进能源动力重点实验室，北京 100190

5．中国科学院 轻型动力创新研究院，北京 100190

6．中国科学院大学 工程科学学院，北京 100049

航空发动机实际运行（如战斗机发射导弹、飞机编队飞行、舰载机在航母上垂直/短距起降、客机飞过闪电区等）中都会在发动机进口产生温度畸变。吸入高温燃气或者蒸汽后会降低发动机稳定裕度，易于引发失稳［1-3］。研究总温畸变对发动机（压气机）的稳定性和性能影响具有重要意义。为此，国内外的研究机构和研究人员们利用试验、理论分析和数值仿真手段对发动机（压气机）进气总温畸变展开了大量研究工作并积累了丰富成果。

试验方面，美国航空航天局刘易斯研究中心的Rudey 和Antl［4］利用氢气燃烧器产生总温畸变，对某双轴涡扇发动机进行了总温畸变试验；试验结果表明高压压气机是对温度畸变最敏感的部件，总温畸变强度和高温区范围均会造成稳定边界下移。中国燃气涡轮研究院的叶培梁和刘大响［5］对某小涵道比涡扇发动机进行了周向总温畸变下稳定性评定试验；试验确定了对该发动机的稳定性影响最严重的一组温度畸变参数，发现失速首先发生在高压压气机中。

理论分析方法是基于压气机的数学模型把进气温度畸变作为输入参数，利用模型的输出参数实现快速分析压气机性能变化。目前研究进气畸变对压气机稳定性影响的模型有平行压气机模型［6］、激盘模型［7］、体积力模型［8-9］等。美国阿诺德工程发展中心的Hale 等［10-12］基于体积力思想，将通过流线曲率法获得的叶轮机械源项耦合到三维欧拉求解器中，发展了三维计算程序TEACC（Turbine Engine Analysis Compressor Code），利用该程序定量评估了进气畸变对某三级军用风扇性能和稳定性的影响。郭晋等［13］通过结合三维体积力和经典二维平行压气机模型提出了一种混合保真度计算模型；利用该模型以较低计算成本定量评估了复杂进气畸变对某大涵道比发动机的性能影响，并捕捉到内部流场的三维特征。李秋实等［14］利用体积力模型将叶片排和进气道-风扇相互作用等作为源项耦合到COMSOL-CFD 程序中，建立了进气道-风扇耦合模拟方法；该模型较好地模拟出了进气道-风扇系统的特性性能及流场性能。叶巍等［15-16］通过前人提出的畸变传递模型［17］研究了进气温度畸变对某发动机稳定性和性能的影响；结果表明稳定裕度的损失更多取决于畸变强度，而不是畸变的周向范围；较高转速下发动机抗温度畸变能力明显强于中低转速；在发射的温度畸变强度下发动机已失去气动稳定性，必须使用防喘系统。张百灵等［18］以刘易斯研究中心设计的5 级压气机的前3 级为研究对象建立了一个压缩系统的模型，结合体积力方法，通过求解非稳态三维欧拉方程较为准确地计算了周向总温畸变的传递特性；分析发现周向总温畸变经过压气机后强度衰减了19%，高温区的周向位置偏移约80°，且总温畸变强度在转子内发生局部增大现象，第1 级转子失速的可能性最大。

数值仿真方面，Weston 等［19］对进气总压畸变条件下的某3 级风扇展开全环数值仿真，研究表明经过风扇后总压畸变引发了总温畸变，越接近失速工况点，总温畸变强度越大，这与转子叶片周围输入的功有关，运行在近失速工况点时转过全环过程中第1 级转子的单个叶片做功量变化范围可达25%。李志平等［20］利用数值模拟手段对某单级轴流压气机进行了不同畸变强度的压力-温度组合畸变对稳定性和性能影响的研究；通过近失速工况点转子叶顶区二维流线的分析发现组合畸变下压气机失稳机理仍是泄漏流从转子叶片前缘溢出。尤延铖等［21］总结概述了国内外在航空发动机进气总温畸变方面的研究工作，包括进气总温畸变来源、温度畸变发生装置及各类总温畸变评定标准，最后列举分析了针对总温畸变的发动机防喘控制技术优缺点，指出对进气总温畸变产生机理、传递和影响等研究急需加强。

通过上述研究发现在进气总温畸变试验方面主要是针对整机展开研究，但由于整机试验成本昂贵、周期漫长等问题，近年来公开的文献较少；采用理论分析可实现进气畸变对发动机（压气机）稳定性和性能影响的快速预测，但是对内部流场细节研究有所不足；此外，目前总温畸变下的高精度非定常计算工作较少，主要聚焦于压气机进口总压畸变引发的总温畸变或总压总温复合畸变条件下，畸变区在压气机内部的传播规律及对压气机性能的影响。而针对进气总温畸变条件下压气机性能变化的背后物理机理和失速现象有待进一步深入研究。相关试验数据［22］表明径向温度畸变影响较小，通常忽略不计。因此本文对Darmstadt 跨声单级压气机展开了周向总温畸变条件下全环非定常数值模拟研究，分析失速过程中压气机内部流场变化，以期揭示总温畸变下该压气机发生失速的动力学机理。

1 研究对象

研究对象为德国Darmstadt 跨声单级压气机试验台（如图1 所示）。该压气机由德国MTU 航空发动机公司和德国航空太空中心设计并优化［23-25］，转子叶片在轮毂附近弯曲度较高且在叶顶附近很薄，整个工作范围内静子叶片没有流动分离迹象且出口角分布均匀，是涡扇高压压气机前级的典型代表。压气机采用800 kW 直流驱动，通过变速器改变轴速度，最大转速为20 500 r/min，最大扭矩为350 N·m。压气机测量截面有级进口面（ME15）、转子进口面（ME21）、级出口面（ME30），压气机性能特性是根据级进口面和级出口面的面平均参数计算得到的，已公布的试验数据包含100%和65%设计转速结果。表1总结了试验台的关键参数，更详细的数据见文献［26-27］。

表1 Darmstadt 跨声压气机的关键参数Table 1 Key parameters of Darmstadt transonic compressor

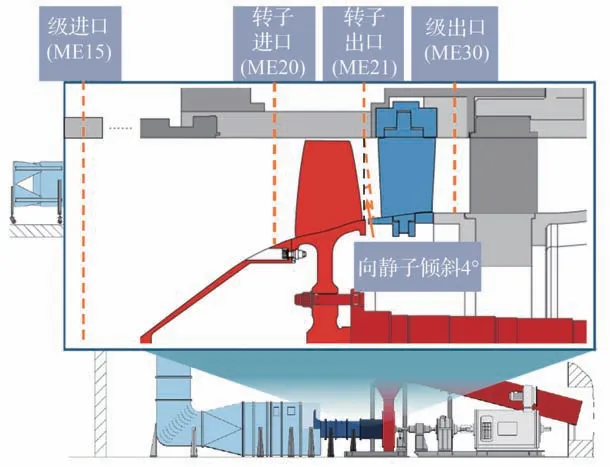
图1 Darmstadt 跨声压气机试验台Fig.1 Test rig of Darmstadt transonic compressor

2 数值模拟方法

2.1 数值设置

通过Ansys CFX 软件求解雷诺平均Navier-Stokes 方程。计算设置采用了标准k-ω湍流模型［28］，壁面为绝热无滑移，流体介质为理想气体。对于均匀来流，采用具有周期性边界条件的单通道定常计算，进口边界条件设置为公布的试验测量值［27］，即进口总压为99 kPa、进口总温为295 K、湍流强度为4%、湍流长度尺度为0.09 m。转静交界面类型为Stage（Mixing-Plane）。对进气总温畸变采用全环非定常计算，进口总温设置为180°周向范围的500 K 高总温区和295 K 的低总温区（如图2 所示，图中θ为周向位置），转静交界面类型为Transient Rotor Stator。出口边界条件采用固定背压为30 kPa 的喷嘴，通过调整喷嘴喉部大小获取不同工况点的特性，大量研究［29-31］已证实此出口边界条件的设置可在压气机较小流量工况点使计算稳定，适合压气机失稳计算。求解格式均为高阶求解模式，非定常计算采用隐式双时间步，转子叶片转过一个叶片通道所需的物理时间步长为80 步，每个物理时间步长的虚拟时间步长为10 步。

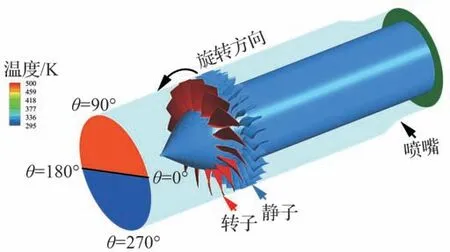
图2 全环计算域示意图Fig.2 Schematic of annulus computation domain

2.2 网格无关性

叶片网格是通过NUMECA/AutoGrid5 生成，采用O4H 拓扑，根据文献［32-33］，网格最大壁面距离y+＜3。针对单通道计算域进行了粗糙、中等、精细3 种不同网格方案的模拟测试。3 组网格方案的网格节点在流向、周向、径向具体分布情况见表2。将100%转速下计算特性和试验数据进行对比，如图3 所示，可见粗糙网格虽可求解出更小流量点，但整体特性上级总压比和等熵效率低于试验数据；随网格量增大，特性线逐渐向右上角移动，折合流量、级总压比和等熵效率的数值更大，与试验值吻合较好；同时中等网格和精细网格求解的失速裕度及特性差距很小，没有明显变化。从求解精度和计算资源角度综合考虑，最终选择了中等网格量，即单通道计算域的网格量约为247 万，全环计算域的网格量约为5 900 万。

表2 网格流线、周向、径向分布Table 2 Mesh distributions at streamline， circumferential and radial directions

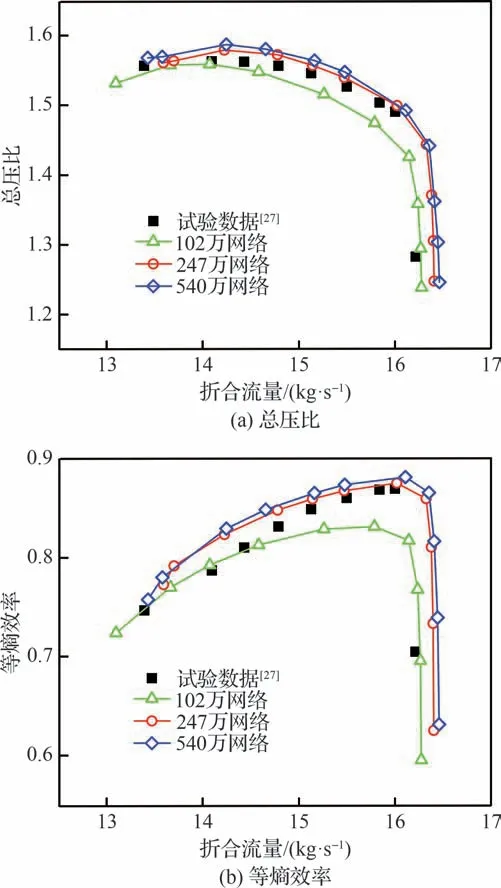
图3 不同网格下压气机特性与试验数据［27］对比Fig.3 Comparison of compressor characteristics for different meshes with test data［27］

3 均匀进气结果与分析

3.1 数值结果验证

验证过程是将数值模拟结果和试验数据进行对比，量化数值仿真的精度，也是进行研究的第一步。65%和100%转速压气机级总压比和等熵效率与试验数据的对比如图4 所示，可看出数值模拟得到的特性和试验值吻合较好，同时能准确捕捉不同转速下压气机的近失速点和堵塞点。

图4 数值结果与试验数据［27］对比Fig.4 Comparison of numerical results with test data［27］

为进一步验证数值模拟方法的准确性，图5 给出了100%转速下最高效率（Peak Efficiency，PE）点和近失速工况（Near Stall，NS）点的级出口面参数径向分布对比，图中mC为折合流量。不同工况点级出口面的总压比和总温比径向分布对比如图5（a）和图5（b）所示，模拟值的总压比在叶根和叶尖处相较于试验数据略大，而总温比整体吻合较好。从PE 点到NS 点级总压比径向分布变得不均匀，NS 点靠近叶根和叶顶区域，均有较大的总压分布；而级总温比在60%叶高以上温梯度大且变化范围较大。尽管数值模拟结果与试验数据在部分叶高有一定偏差，但结果与其他研究人员采用不同求解器的计算结果［27，33］趋势基本一致。

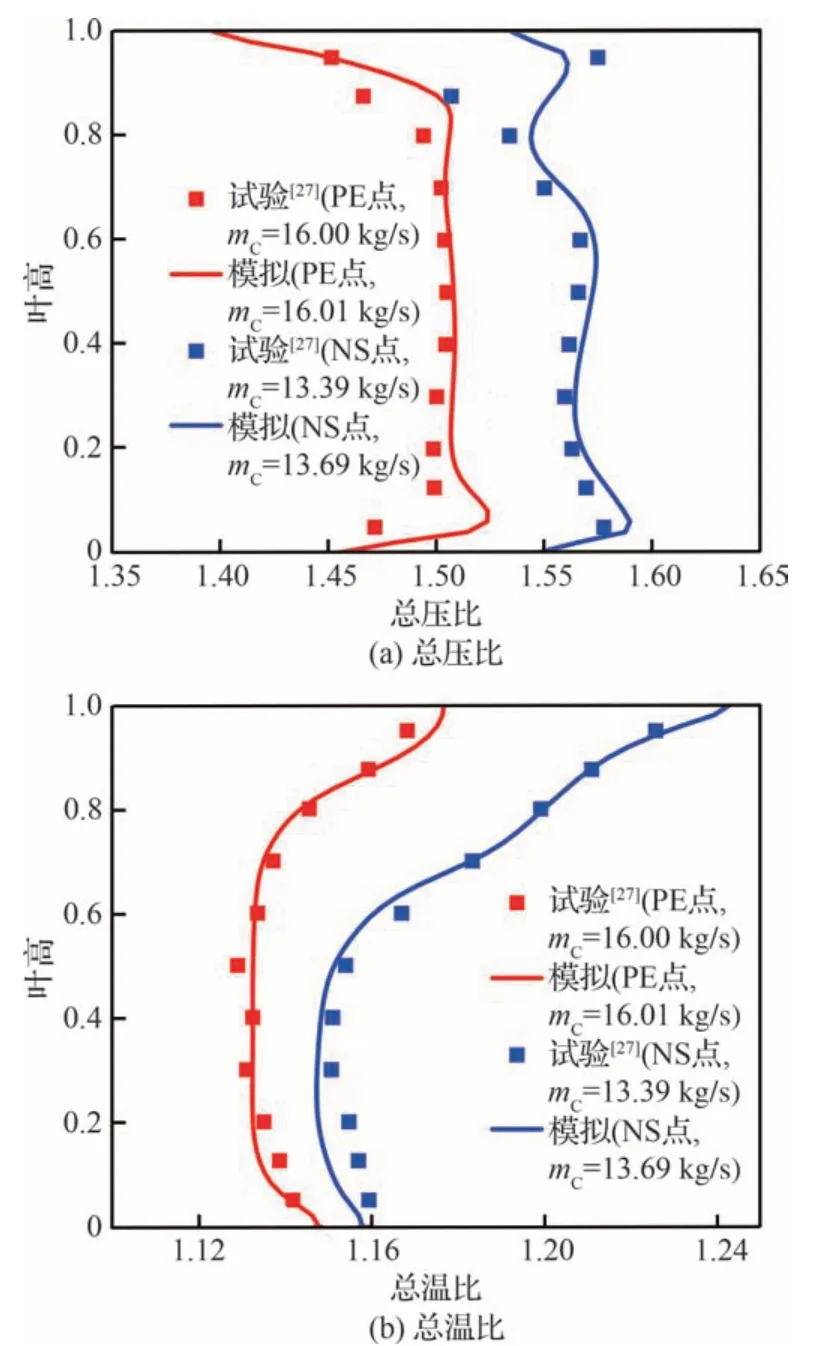
图5 级出口面（ME30）参数与试验数据［27］对比Fig.5 Comparison of parameters at stage exit （ME30）with test data［27］

试验台的静子轮毂空腔会存在泄漏流，根据文献［34］，考虑0.5%的泄漏流量后数值模拟结果和试验数据在径向分布上的对比会更好，工作中未考虑泄漏流的影响。

最后从内部流场角度对3 个不同的典型工况（近失速点、最高效率点和近堵塞点）的静压参数进行对比。数值模拟结果提取的99.9%叶高静压云图与试验转子叶顶区的壁面静压云图［27］对比如图6 所示，图中LE 为前缘（Leading Edge），TE 为尾缘（Trailing Edge），可见数值模拟能精确捕捉脱体激波、叶顶泄漏流的轨迹和通道激波的位置。图3～图6 的对比充分验证了数值仿真设置的正确性。

图6 数值模拟所得内部流场与试验数据［27］的对比Fig.6 Comparison of internal flow fields obtained from numerical simulation with test data［27］

3.2 均匀进气失速特征

文献［35］的数值研究表明诱发该压气机失速的先兆波为突尖型，计算模拟捕捉到前缘溢出和尾缘回流的流动特征。在失速模拟中从失速前最后一个稳定解开始节流。失速特征如下：在约1 rev 后压比上升，质量流量开始下降；在3 rev 左右达最小值后质量流量和压比又开始增加，在约6 rev 后达最终失速状态。通过失速模拟中攻角变化的研究确定了该压气机失速扰动发生在转子叶顶区域，且在失速先兆阶段动叶周围的流动发生前缘溢出和强烈的尾缘回流现象，为突尖型失速先兆。模拟过程中失速团的周向传播速度约为1/3 转子转速。文献［36］的试验研究表明该压气机以突尖型先兆启动失速，形成一个单独的失速团并绕环旋转。试验中，100%转速下从稳定极限点关小阀门。在约5 rev 时失速团尺寸最大，对应局部流量最小，传播速度约为0.44 倍转子转速；随后失速团尺寸开始减小，约15 rev 时失速团尺寸达最小，对应局部流量最大，传播速度约为0.52 倍转子转速。试验观测到随流量减小失速团尺寸增大、传播速度变慢的特性，失速团的尺寸和传播速度随压气机接近稳定的失速点而震荡。

4 总温畸变下压气机失速分析

4.1 主要参数变化

为分析进气总温畸变影响压气机性能的物理机理，表3 展示了PE 点（折合流量为14.58 kg/s）压气机进口面高温畸变区和低温非畸变区关键参数的对比，可见高温畸变区总温为500 K，低温非畸变区总温为295 K；总压均为99 kPa；高温区气流密度为0.656 8 kg·m-3，低温区气流密度1.109 4 kg·m-3；高温区轴向速度为141 m·s-1，而低温区轴向速度为109 m·s-1；高温区密流为93 kg·m-2·s-1，低温区密流为121 kg·m-2·s-1。可见总温畸变对压气机的主要影响为高温区气流密度大幅减小，轴向速度增大。同时高温畸变区工作在低折合转速线上，因此总温畸变下压气机工作特性点往左下角移动。

表3 高、低温区关键参数对比Table 3 Comparison of key parameters in high and low temperature regions

4.2 不同周向位置总压径向分布

为总结总温畸变下压气机内部流场随不同工况点的变化规律，对不同周向位置处时均总压径向分布情况进行分析。在总温畸变非定常计算的PE 点（折合流量为14.58 kg/s）和NS 点（折合流量为13.46 kg/s）的转子出口面，每隔45°周向角度提取总压径向数据进行对比。周向角度位置定义如图7 所示，背景为NS 点转子出口面时均总压云图。

图7 转子出口面周向角度位置Fig.7 Position of circumferential angle at rotor exit surface

图8 （a）、图8（b）分别展示了总温畸变下PE工况点0°～180°和180°～360°不同周向位置的总压径向分布情况，可见在0°、45°、90°、135°和180°的高温区周向位置，总压径向分布逐渐变窄。不同周向位置的总压径向分布形式比较类似，叶中区域分布均匀，而叶顶叶根区域由于端壁边界层、角区等导致流动损失进而使总压存在较大梯度；在180°、225°、270°、315°和360°的周向位置，总压径向分布逐渐变宽。

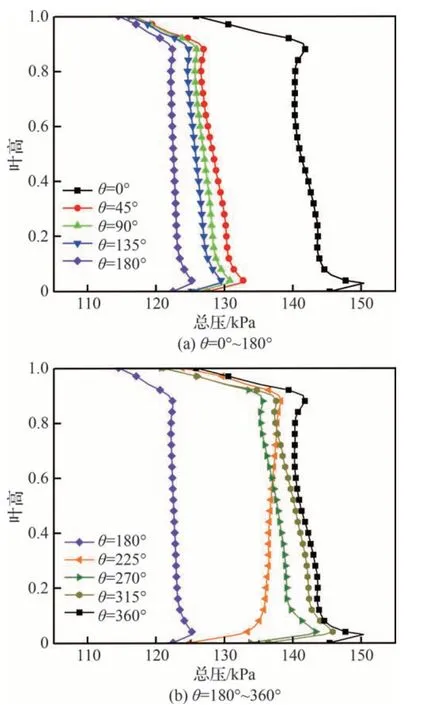
图8 PE 点转子出口面不同周向位置处总压径向分布Fig.8 Radial distributions of total pressure at different circumferential positions of rotor exit for PE condition

图9（a）、图9（b）分别展示了总温畸变下NS工况点0°～180°和180°～360°不同周向位置的总压径向分布情况，可见在0°、45°、90°、135°和180°的高温区周向位置，总压径向分布呈现逐渐变窄的趋势。在180°、225°、270°、315°和360°的低温区周向位置，总压径向分布呈现逐渐变宽的趋势且分布较为不均匀。转子出口面总压云图如图7所示，在225°周向位置处，叶根区域的总压较小，而叶顶区域存在一个高总压区，总压径向分布不均匀。这是由于畸变引起气流角沿周向分布不同，且沿径向也发生迁移，从而加功量不同，导致总压在不同周向位置的径向分布差异。

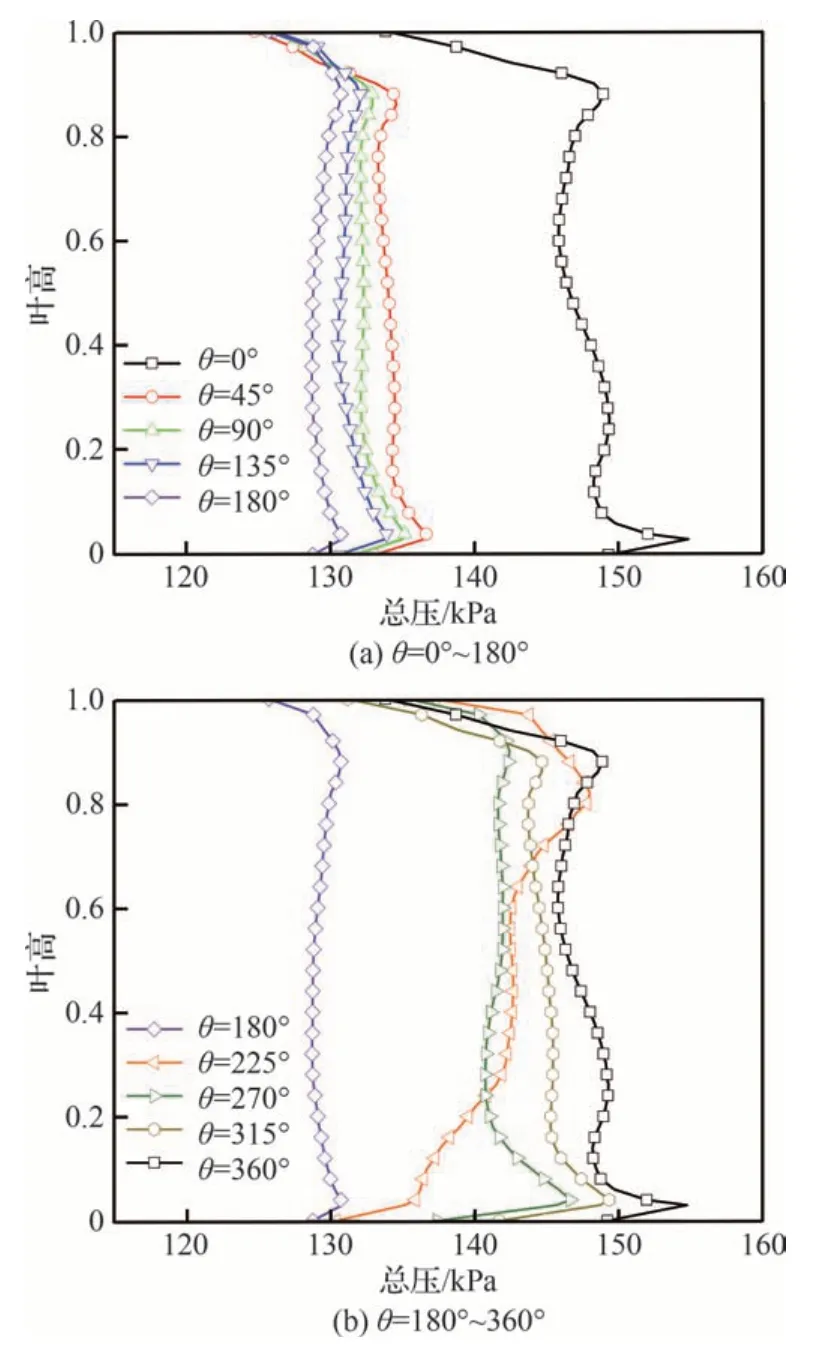
图9 NS 点转子出口面不同周向位置处总压径向分布Fig.9 Radial distribution of total pressure at different circumferential positions of rotor exit for NS condition

图10 为不同叶高处和具有相同喷嘴喉部面积的、均匀来流的、绝对周向气流角的周向分布对比。定义逆转子旋转方向为绝对周向气流角正方向。结合图11 中的速度三角形，可见在0°～180°范围绝对周向气流角α由正值减小到负值，相对气流角β逐渐减小，因此攻角减小，叶片载荷减小，总压减小。在180°～360°范围，绝对周向气流角α由负值增大到正值，相对气流角β逐渐增大，因此攻角增大，叶片载荷增大，总压增大。并且对于该压气机而言，总温畸变下周向气流角变化范围在叶根区域最大，从10%叶高到90%叶高逐步减小。以上研究结果表明，在转子由低温非畸变区转入高温畸变区时攻角最大，因此猜测此处可能最先发生失稳。为验证这一猜想，接下来进一步对失速过程进行了分析。

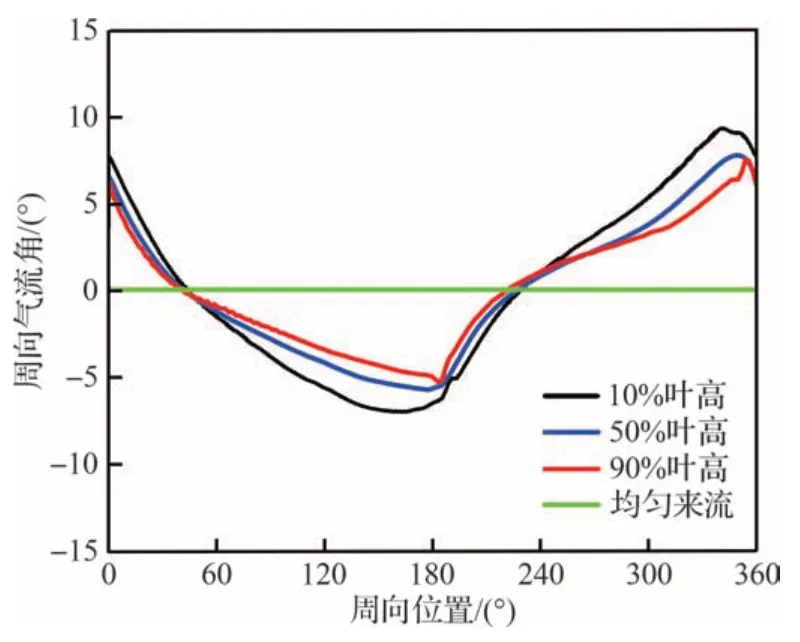
图10 转子进口绝对周向气流角Fig.10 Absolute circumferential flow angle at rotor inlet

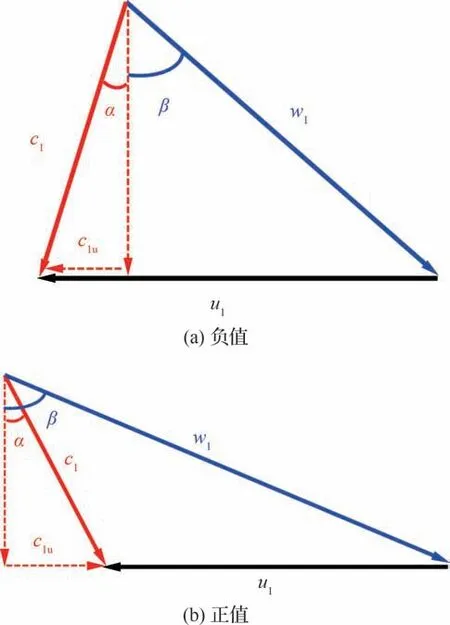
图11 速度三角形中绝对周向气流角Fig.11 Absolute circumferential flow angle in velocity triangle

4.3 总温畸变数值结果与分析

进气总温畸变条件下，压气机的级总压比特性曲线如图12 所示。从图12 中可见由一个稳定解过渡到失速状态，总压比和折合流量先略微升高，然后迅速下降，再回升，以此循环往复呈现周期性变化特征。

图12 总温畸变下压气机特性Fig.12 Compressor performance characteristics with total temperature distortion

进气总温畸变条件下失速过程中压气机进口物理流量随转数的变化情况如图13 所示，物理流量和折合流量的换算关系为

图13 总温畸变下失速过程压气机进口物理流量Fig.13 Physical flow rate at compressor inlet during stall process under total temperature distortion

式中：mC为折合流量；m为物理流量为级进口总压；为级进口总温。

从10 rev 开始由一个稳定的工况解轻微减小喷嘴喉部面积。由图13 可见从11 rev 开始物理流量迅速从10.8 kg/s 下降到7.6 kg/s，随后升高到11.3 kg/s，往复变化，且物理流量的震荡幅度有轻微减小，变化趋势与图12 中压气机特性变化相符合。

4.4 失速过程轴向速度分布

图14 展示了不同转数t下转子出口面的轴向速度分布云图，可见在11 rev 轴向速度沿周向分布较均匀，未出现回流；在13 rev 出现2 个较大失速团和较小失速团（黑虚框），且低轴向速度区域近乎占据了整个转子出口面一半周向范围，此时压气机已经处于失速状态；转到16 rev 和20 rev时失速团合并为1 个，且占据的周向范围大幅缩小；转到23 rev 和27 rev 时失速团变为1～2 个较大失速团和若干小失速团，大约占据整个转子出口面1/3 周向范围。结合图13 物理流量随转数时间的震荡变化情况看，当物理流量较小（如13 rev 和27 rev）时失速团的数量较多、占据范围较大，堵塞程度较严重；当物理流量较大（如16 rev 和20 rev）时失速团数量较少、占据范围较小，堵塞程度较轻；由此计算出流量振荡频率约为75.0 Hz。

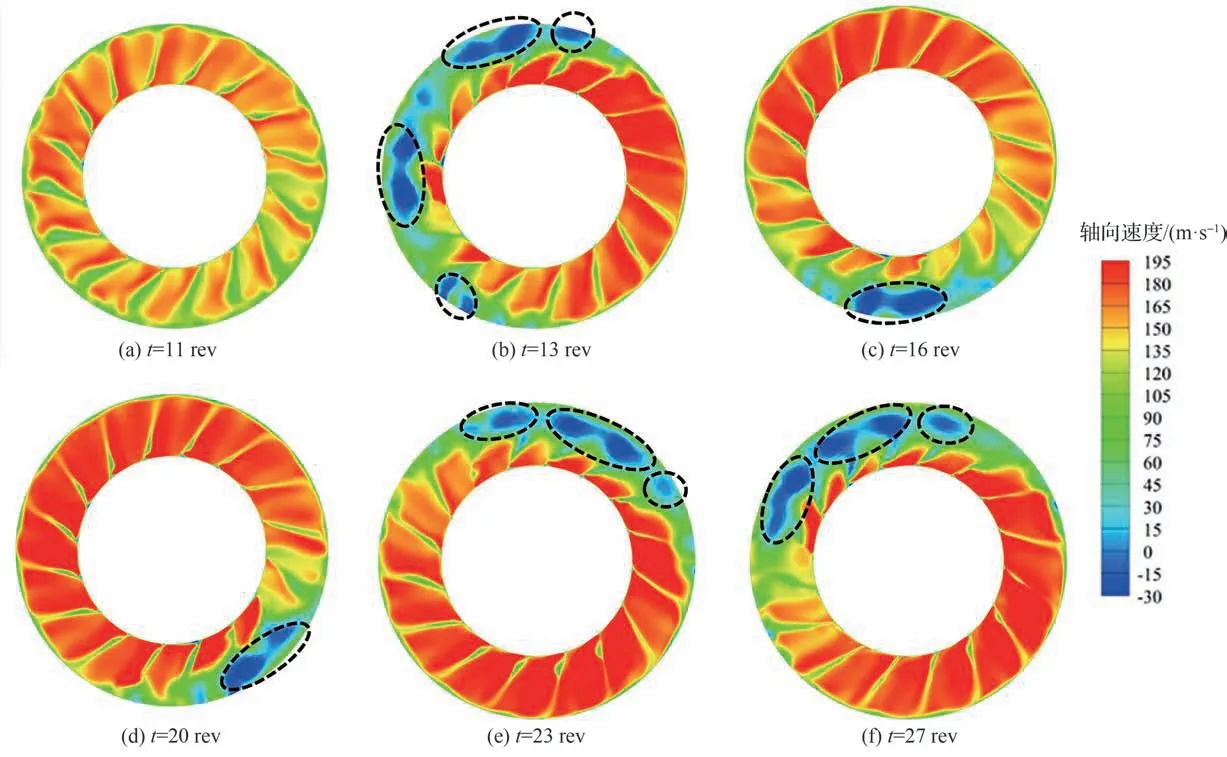
图14 失速过程的轴向速度云图Fig.14 Axial velocity contours during stall process

4.5 失速过程轴向速度为0 的等值面分布

为进一步分析失速过程中失速团的体积大小和空间分布，图15 展示了不同转数瞬态解的转子域中轴向速度为0 的三维等值面分布云图。在全环域瞬态解中生成轴向速度为0 的等值面，这个等值面可看作失速团的边界，等值面围成的空间大小可看作失速团的体积，这种方法是由Zhang 和Vahdati［31］提出的。从图15 中可清晰看到进气总温畸变条件下压气机失速过程中失速团的空间分布集中在叶顶区域。随着转子旋转时间推进，失速团的空间位置在叶顶沿周向移动，失速团的体积也在不断变化。

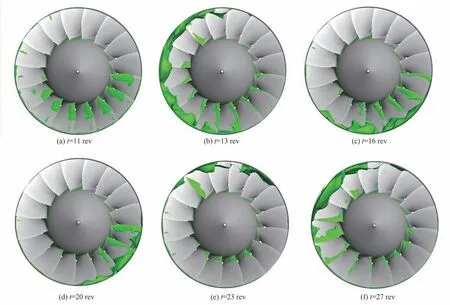
图15 失速过程轴向速度为0 的等值面云图Fig.15 Iso-surface of zero axial velocity contours during stall process

4.6 静压探针信号分析

为进一步确定失速先兆最先出现的周向位置和先兆波类型，在数值计算设置中沿周向均匀布置了12 支绝对静压探针监测转子前缘的静压值变化。探针距离叶片前缘为10%转子轴向弦长，探针的径向位置为99%叶高，探针布局方式和序号如图16 所示。

图16 静压探针的周向布局Fig.16 Circumferential arrangement of static pressure probes

图17 展示了12 支绝对静压探针的压力信号随时间的波动情况，可看出CH10 探针（即压气机转子从低总温非畸变区转入高总温畸变区的周向位置处）最先监测到明显压力波动，随后顺转子旋转方向的探针压力波动幅值增大，表明转子叶片前缘的非定常波动增强，压气机由稳定的近失速工况点转入失速状态。失速先兆的周向传播速度约为88.9%转子转速，失速初期失速团的传播速度约为66.0%转子转速。图18（a）和图18（b）展示了11.0 rev 和11.5 rev 时98%叶高的速度矢量和轴向速度云图，可见在11.0 rev 时只观测到叶顶泄漏流从转子前缘轻微溢出；在11.5 rev 时可看到叶顶泄漏流在转子前缘明显溢出和尾缘回流现象，此时叶片通道发生堵塞，最终形成失速扰动。这符合Vo 等［37］通过单/多通道压气机定常/非定常数值计算提出的突尖型失速先兆的准则：叶顶泄漏流从转子叶片前缘溢出和尾缘跨通道回流。因此总温畸变下诱发旋转失速的先兆波为突尖型失速先兆。

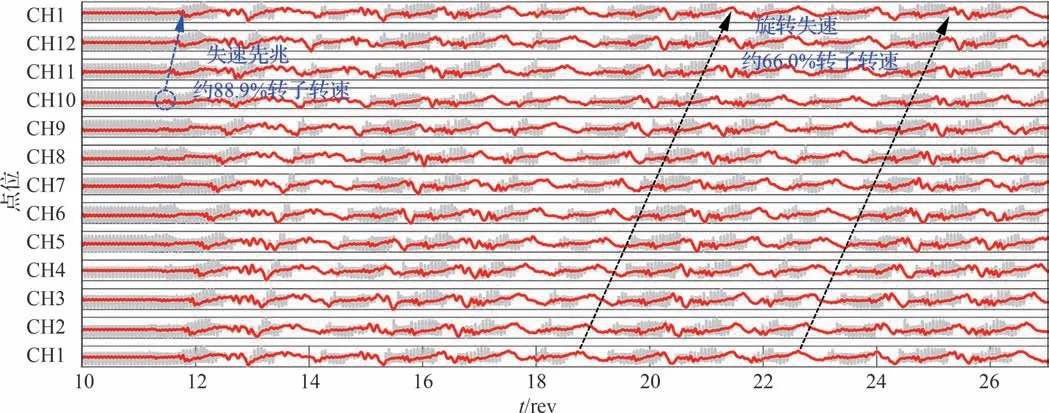
图17 周向静压探针的压力信号Fig.17 Pressure signals of circumferential static pressure probes

图18 不同时刻速度矢量和轴向速度云图Fig.18 Velocity vector and axial velocity contour at different times

5 结 论

对德国Darmstadt 跨声压气机进行了均匀进气条件下单通道定常数值模拟，数值结果与试验数据吻合较好，验证了计算设置的准确性；进行了总温畸变条件下的压气机全环非定常数值模拟，对失速过程进行了研究，得到以下结论。

1） 在周向范围180°、高温畸变区500 K 的周向总温畸变条件下压气机总压比-流量特性大幅下降，在失速过程中特性曲线呈周期性震荡现象，当物理流量较小时对应压比较小，失速团数量较多、占据范围较大，堵塞程度较重；当物理流量较大时对应压比较大，失速团数量较少、占据范围较小，堵塞程度较轻。

2） 总温畸变下不同周向位置处的总压径向分布不同。顺转子叶片旋转方向总压在高温区逐渐减小，在低温区逐渐增大，且在叶根区域变化最为明显。

3） 总温畸变下最先发生压力扰动的周向位置是转子转入高温畸变区处，诱发旋转失速的先兆波为突尖型失速先兆。

4） 总温畸变下失速先兆的周向传播速度约为88.9%转子转速，失速初期失速团的传播速度约为66.0%转子转速，高于均匀进气下失速团的传播速度。